Category theory for programmers. On fingers

Hello colleagues.







Developing our unflagging interest in serious , one might say, academic literature, we got to the theory of categories . This topic in the famous presentation by Bartosz Milevsky has already appeared on Habré and by now it can boast of such indicators:







It is all the more pleasant that we managed to find relatively fresh material (January 2020), which serves as an excellent and at the same time as brief as possible introduction to the theory of categories. We hope that we will be able to interest you in this topic.



If you and I, dear reader, faced similar problems, then you were once tormented by the question "what the hell is a monad ?!" Then you googled this question, slipping stealthily down the rabbit hole of abstract math , getting tangled up in functors , monoids , categoriesuntil they noticed that they had already forgotten what question brought you here. This experience can be quite overwhelming if you've never seen functional programming languages ​​before, but don't worry! I have studied many pages of dense mathematics for you and watched hours of lectures on this topic. So to save you the trouble, I'll summarize the topic here and also show you how you can apply category theory so that you can think (and write code) in a functional style right now.



This article is intended for anyone who considers himself a "newbie" in the field of functional programming and is just getting started with Scala, Haskell or another similar language. After reading this article, you will feel a little more confident in interpreting the foundations of category theory and identifying its principles "on the ground." Also, if you've ever tried your hand at theoretical mathematics, refrain from directly mentioning the concepts that are touched upon here. As a rule, much more can be said about each of them than is written here, but this article will be enough for an inquisitive programmer.

The basics

So what exactly is a category and how does it relate to programming? Like many concepts used in programming, a category is a very simple thing with a fancy name. This is just a labeled directed graph with some additional restrictions. Each of the nodes in a category is called an "object" and each of its edges is called a "morphism".







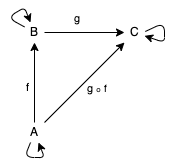
As you might have guessed, not every directed graph is a category; for a graph to be considered a category, some additional criteria must be met. In the next picture, we note that each object has a morphism that points to itself. This is the identical morphism, and each object must have such that the graph is considered a category. Next, notice that the object Ahas a morphism findicatingB, and, likewise, the object Bhas a morphism gpointing to C. Since there is a path from Ato Band from Bto C, obviously there is a path from Ato C, right? This is the next requirement categories for morphisms necessarily associative composition must be carried out, so that for a morphism f: A = > B , and g: B = > Cthere is a morphism h = g(f): A = > C.



These calculations may already seem a little abstract, so let's look at an example that satisfies this definition and is written in Scala.

trait Rock
trait Sand
trait Glass
def crush(rock: Rock): Sand
def heat(sand: Sand): Glass

I think this example makes the relationship a little easier. Erasing stones into sand is a morphism that transforms an object rockinto an object sand, while smelting glass from sand is a morphism that transforms an object sandinto an object glass. In this case, the composition of these relations will definitely look like

val glass: Glass = heat(crush(rock))

There are also identity functions (defined in PredefScala), since for any object it is not difficult to write a function that returns the same object. Hence, this system is a category, albeit quite simple.

Deeper familiarity with categories

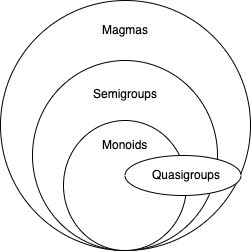
We will now delve a little deeper into the terminology of category theory and start with a category called magma. If you are not yet too familiar with this basic concept, let me explain that magma is just a binary operation, that is, an operation on two values, as a result of which a new value is obtained. In order not to go into details, I will not give here a proof that the set of all binary operations is actually a category, but for those who are interested in details, I recommend reading the following article by Bartosz Milevsky. All arithmetic from addition to multiplication belongs to the subcategories, united by the magmatic category (see diagram).



The following order of inheritance applies here:

• 1. Magma: all binary operations
• 2. Semigroups: all binary operations that are associative
• o : .
• 3. : ,
• o : , (aka )

So, going back to our earlier example, both addition and multiplication are monoids because they are associative (a + (b + c) = (a + b) + c)and have a single element (ax 1 = 1 xa = a). The last circle on this diagram contains quasigroups for which different embedding principles may apply than for semigroups or monoids. Quasigroups are binary operations that are reversible. Explaining this property is not so easy, so I refer you to the series of articles by Mark Siman devoted to this topic. A binary operation is reversible when for any values aand bthere are such values xand ythat allow converting atob... I know it sounds tricky. To make it clear, let's look at the following example of subtraction:

val x = a - b
val y = a + b
assert(a - x == b)
assert(y - a == b)

Please note: it ydoes not participate in the subtraction as such, but the example still counts. Objects in a category are abstracted and can be almost anything; in this case, it is important that for any aand bthat can be generated, these statements remain true.

Types in context

Regardless of your particular discipline, the topic of types should be clear to anyone who understands the meaning of data types in programming. Integer, boolean, floating point, and so on are all types, but how would you describe the ideal Platonic type in words? In his book Category Theory for Programmers, which turned into a series of blog posts, Milevsky describes types simply as "sets of values." For example, a boolean is a finite set containing the values ​​"true" and "false" (false). A char is a finite set of all number-letter characters, and a string is an infinite set of char.



The problem is that in category theory we tend to move away from sets and think in terms of objects and morphisms. But the fact that types are simply sets is inevitable. Fortunately, there is a place in category theory for these sets, since our objects are abstractions and can represent anything. Therefore, we have every right to say that our objects are sets, and further consider our Scala programs as categories, where types are objects and functions are morphisms. To many, this may seem painfully obvious; after all, in Scala we are used to dealing with objects, but it is worth pointing out that explicitly.



If you've worked with an object-oriented language such as Java, then you're probably familiar with the concept of generic types. These are things likeLinkedListor, in the case of Scala, Option[T]where Trepresents the underlying datatype stored in some structure. What if we wanted to create a mapping from one type to another so that the structure of the first type is preserved? Welcome to the world of functors, defined as mappings between categories to maintain structure. In programming, you usually have to work with a subcategory of functors, called endofunctors, that help map a category to itself. So I'll just say that when I talk about functors I mean endofunctors.



As an example of a functor, let's look at the Scala type Option[T]in conjunction with our previous example, which mentioned stone, sand, and glass:

val rockOpt: Option[Rock] = Some(rock)

Above we have the type Rockas we defined it earlier, but wrapped in Option. This is a generic type (and not only, more on this below), telling us that an object is either a specific entity that we are looking for, or Nonethat can be compared with nullin other languages.



If we did not use functors, then we could imagine how we are applying a function crush()to Rock, which would require resorting to an operator if to handle the situation in which it Optionis None.

var sandOpt: Option[Sand] = None
if(rockOpt != None) {
  sandOpt = Some(crush(rockOpt.get))
}

We might say that this is an aside, but please do not use var - such code is bad in Scala for several reasons. Again, getting back to the topic: in Java or C # this would not be a problem. You check to see if your value is of the type you expected to see and do whatever you want with it. But with the power of functors, everything can be done a little more elegantly with the function map():

val sandOpt: Option[Sand] = rockOpt.map(crush)

Boom, one line and you're done. It would be possible to put the first example in one line, using the ternary operator or something similar, but you would not have succeeded so succinctly. This example is truly wonderful in its simplicity. Here's what's going on here: it map()takes a function and maps that function (in a mathematical sense) to itself. The structure is Optionpreserved, but now it contains either Sand, or None, instead of Rockor None. This can be illustrated something like this:







Notice how beautifully everything is lined up, every object and morphism are preserved in both systems. Consequently, the morphism at the center is a functor representing the mapping from Tto Option[T].

Together

Now we can finally get back to the original question “what the hell is a monad”? There is an answer that you can stumble upon blindly if you just try to Google it, and it sounds like this: a monad is just a monoid in the category of endofunctors, which is often followed by a very sarcastic remark, "what's the problem?" As a rule, in this way they try to jokingly show how difficult everything is in this topic, but in fact, not everything is so scary - after all, we have already figured out what this phrase means. Let's take it step by step again.



First, we know that monoids are associative binary operations, each of which contains a neutral (single) element. Secondly, we know that endofunctors allow us to map a category to itself, while maintaining the structure. So a monad is just some kind of wrapper type (as in the generic types example above) that maintains some method for accepting a function and mapping it to itself. List- this is a monad, Option(like the one that we considered above) is a monad, and someone may even tell you that and Futureis also a monad. Example:

val l: List[Int] = List(1, 2, 3)
def f(i: Int) = List(i, i*2, i*3)
println(l.flatMap(f)) // : List(1, 2, 3, 2, 4, 6, 3, 6, 9)

Deceptively simple, isn't it? At the very least, there should be a feeling that it is not difficult to grasp everything here, even if at first glance it is not entirely clear what the use of such a concept is.