
Removing nodes from a red-black tree is not an easy task, so it makes sense to split it into several parts and consider each case separately.
cartoonbank.ru
In the last article, we examined the rules for forming a red-black search tree and considered the cases of balancing when adding elements.
Now let's talk about deleting items.
Take, for example, this red-black tree:
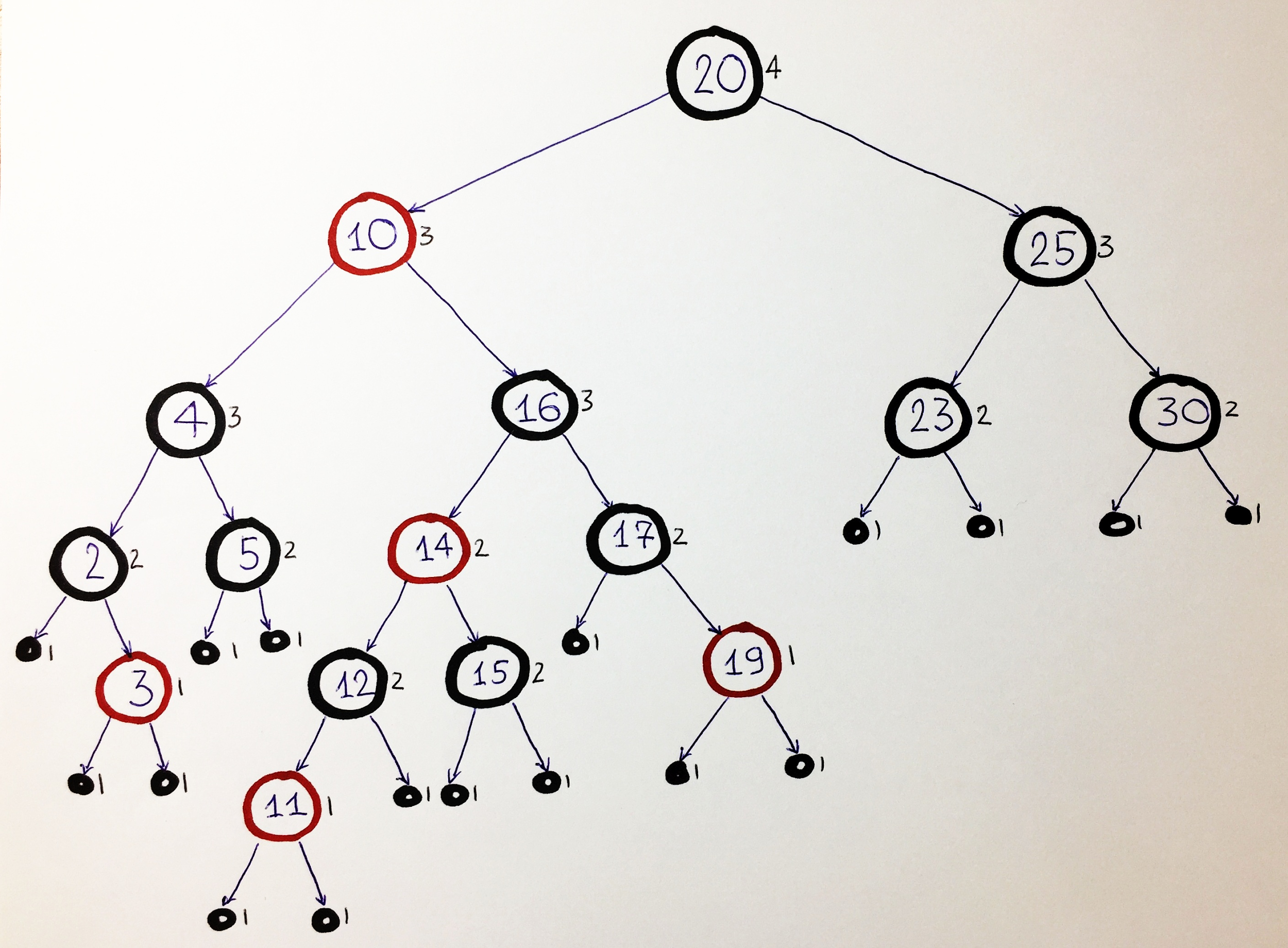
Recall that the main property of a red-black tree is the same black height to the left and right of each node. Therefore, in the figures, next to each node, we will indicate the value of the black height, so that at each stage we can check its stability.
Divide and rule
Removing an element from a red-black tree is not such an easy task as it might seem at first glance, so I propose to divide it into several parts and consider each separately.
First, let's divide the task into two categories:
- color of the removed node: K or H
- number of child nodes: 2, 1 or 0
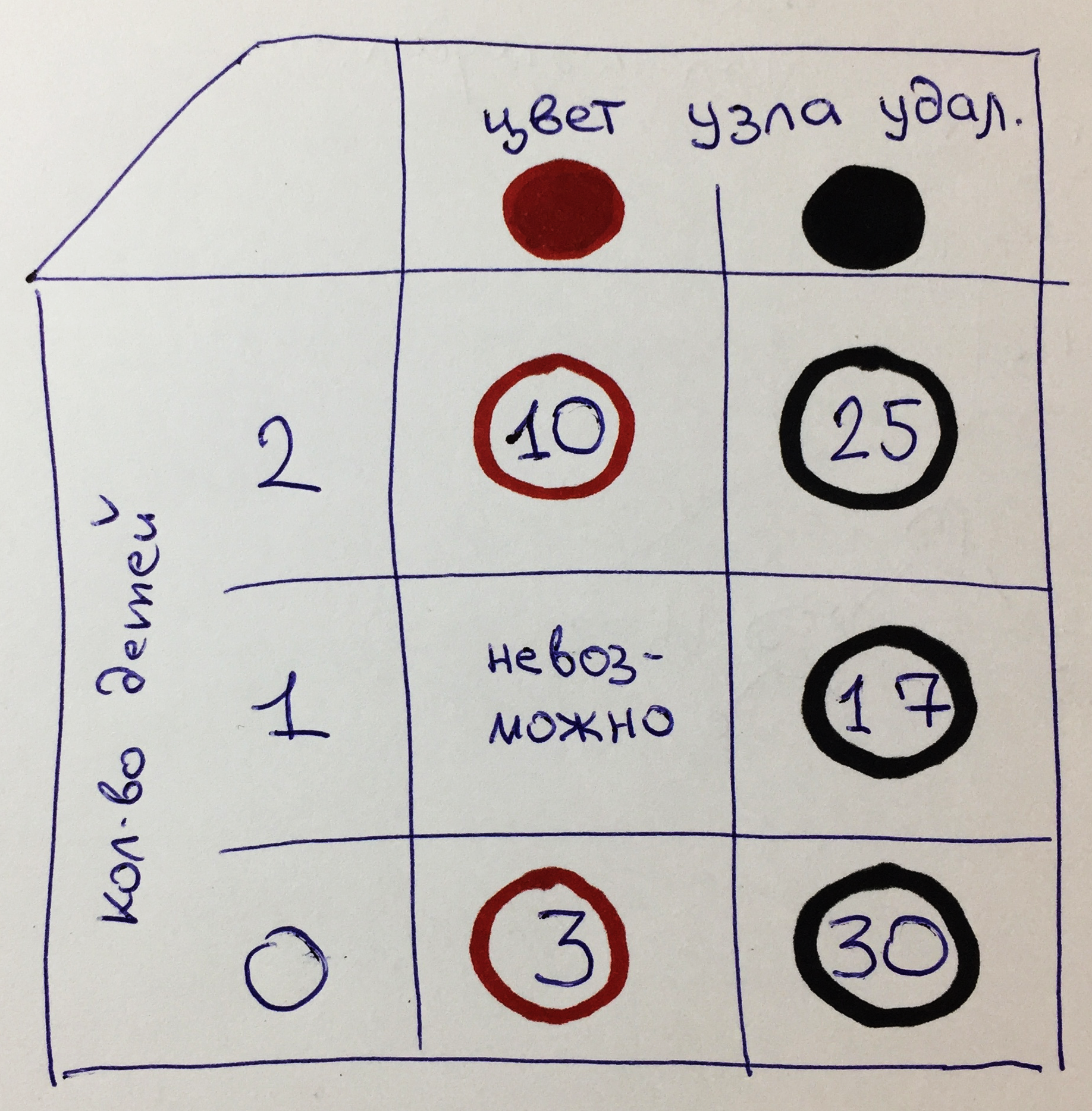
As a result, we get a matrix of 6 options: K2, Ch2, K1, Ch1, K0, Ch0.
For each option, the corresponding node of our tree is indicated.
Let's consider the removal process for each option.
K2 - red knot with two children
The task of deleting a node with two children is reduced to the task of deleting a node with one or zero children.
To do this, you need to find the closest element that is less or more than the deleted one and swap them.

Please note that when swapping elements, you need to change only the values in the nodes, and leave the color the same, so as not to break the tree structure and not change the black height.
After the exchange, you need to remove the item from its new location. It will be either the rightmost element in the left branch (maximum on the left), or the leftmost in the right (minimum on the right), in any case it will not have one child on the left or right. Thus, the task of removing a node with 2 children is reduced to the task of removing an element with 1 or 0 children:
- K2 => K1 or K0
Ch2 - black knot with two children
Similarly to the previous case, we will give an example of deleting black node 16.

As you can see, after the exchange, the task is reduced to deleting an element with one child:
- Ch2 => Ch1 or Ch0
K1 - red knot with one child
If the red node does not have one child, then it has a black NIL element instead and the black height of the red node is 1. Therefore, on the other hand, the black height must also be 1. But since the red node cannot have a red child colors, then his other child should be black. Since the black height must be 1, it can only be a black NIL element, since in the case of a normal black element, the height will be higher.
Thus, K1 case does not take place.
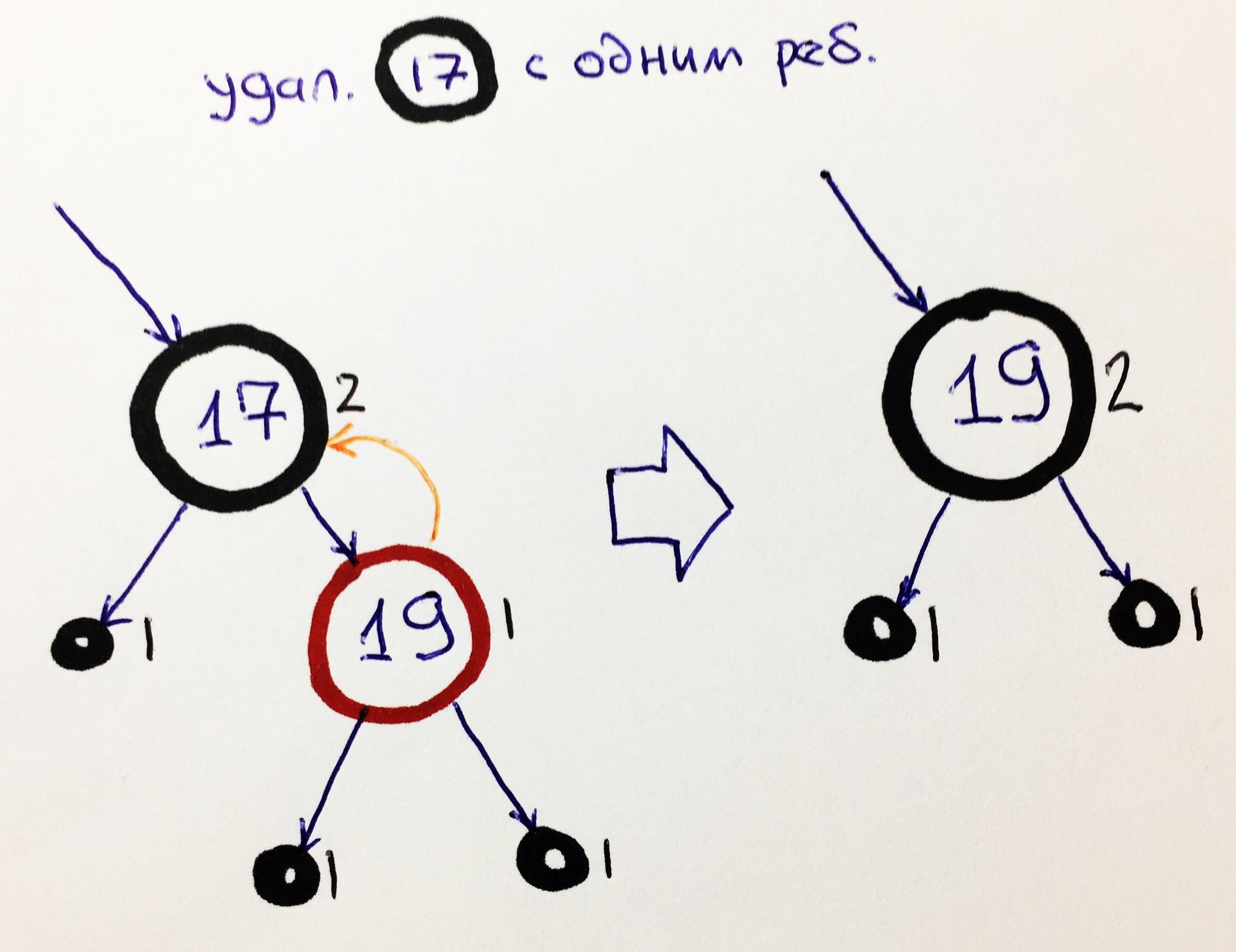
Ch1 - black knot with one child
If the black element does not have one child, then instead there is a black NIL element with a black height 1. Therefore, on the other side there should be a red node without children. To remove such an element, it is enough to transfer the value of the red element to the black node, while the black height will be preserved.
K0 - red knot without children
The simplest case. We simply remove the element, replacing it with a NIL reference:
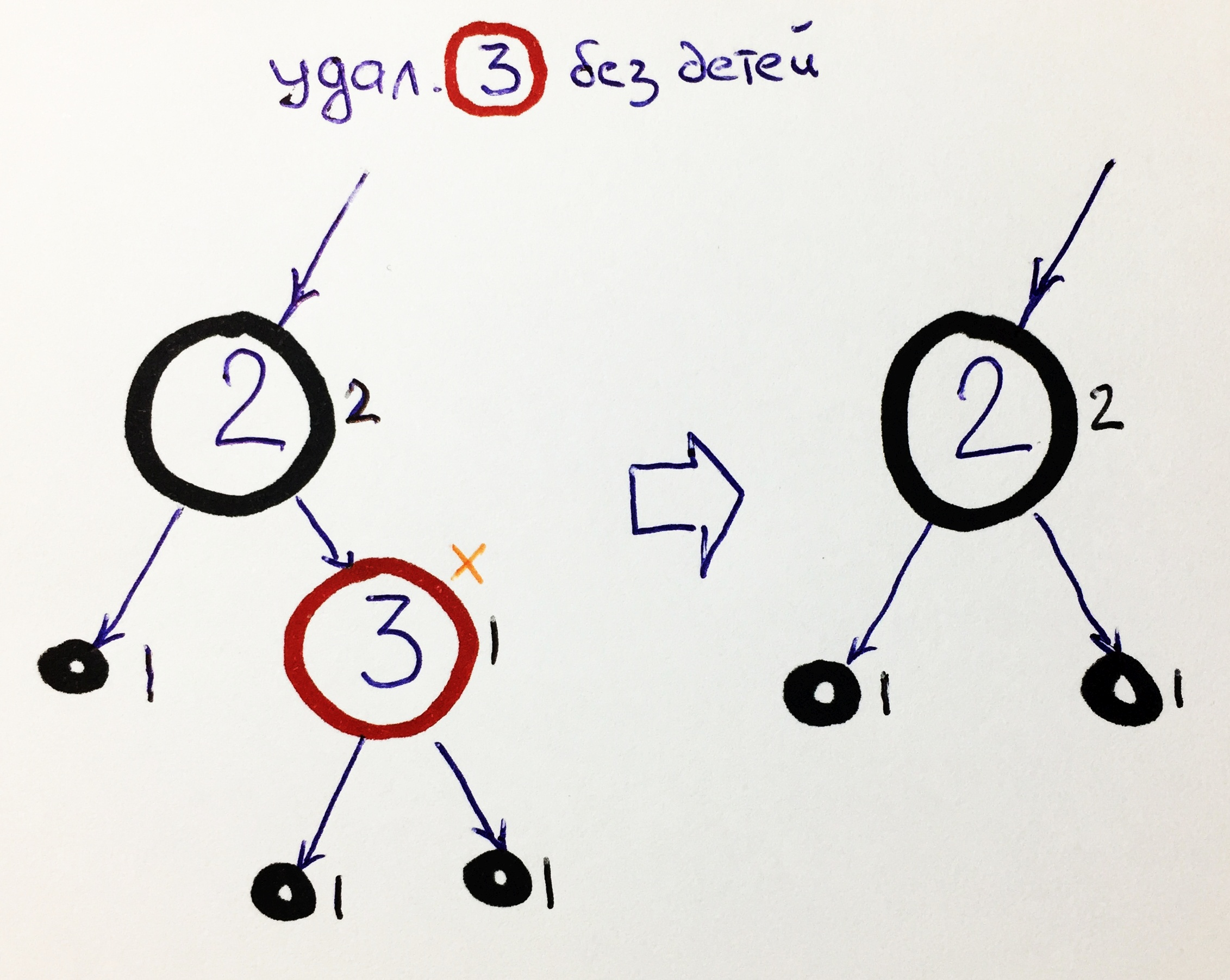
Removing the red element does not change the black height.
CH0 - black knot without children
Removing a black node without children is also very simple: we replace it with a reference to NIL.
Do you think this is almost all? Haha, six times.

After removing the black element, the black height of the subtree changes and you need to balance it for its parent.
The deleted element in the figures is denoted by x, its height - h. When we just start balancing, h = 1, but it can increase with recursive calls.
For definiteness, let us establish that the deleted element was the right child. After removal, its height decreased and became h. This means that the height of the left son remains h + 1. We need to align the heights of the left and right subtrees and make them equal to h + 1.
I suggest dividing the task into several parts again. What options do we have?
The parent can be red or black. The left son can also be black or red. And the right son is always black - it was from there that we came to balancing after removal.
There are 6 different cases to consider:
- KCH1 and KCH2 - the parent is red, the left child is black.
- CHK3 and CHK4 - the parent is black, the left child is red.
- HH5 and HH6 - the parent is black, the left child is black.
We will stock up on patience and popcorn, the most interesting and mysterious lies ahead.
KCH1 - parent red, left child black with black grandchildren
As long as we have the red nodes, we can move and / or recolor them to restore the balance of the black height. In this case, we can lower the red color from the parent to the left son, thus aligning the black height of the parent:

Be sure to double-check from the figure that the black heights of nodes a and b are preserved, and the height of the entire subtree has become the same and equal to h + 1.
KCH2 - parent is red, the left child is black with the left red grandson.
In this case, repainting alone is not enough. We need to make a small turn to the right between nodes 3-7. As a result, we will be able to increase the height of the right subtree to h + 1: A
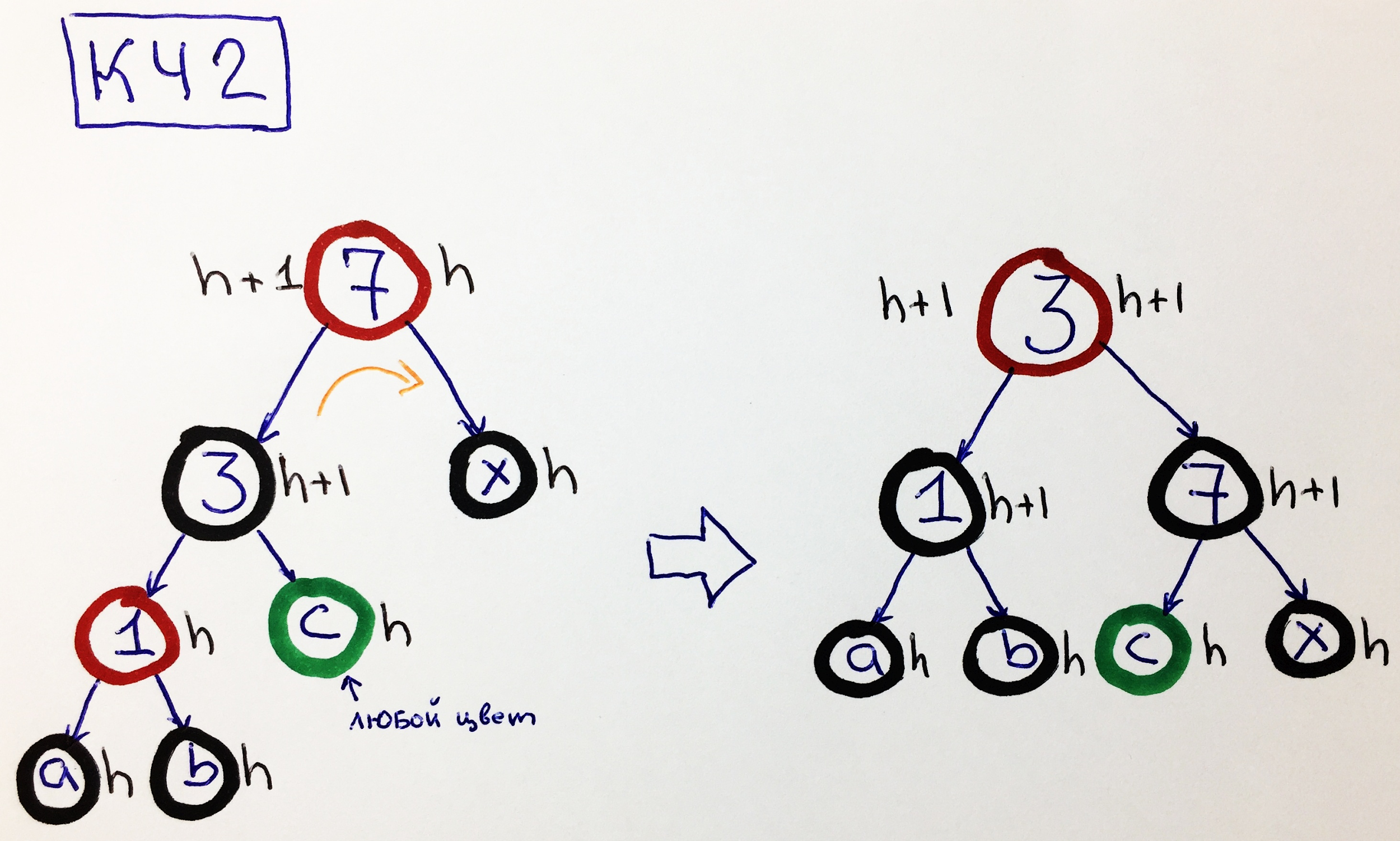
green node means that it can be either black or red.
Note. If node “1” is black, and “c” is red, then the problem can be reduced to variant HH5.
CHK3 - the parent is black, the left son is red, the right grandson has black great-grandchildren
Having black great-grandchildren allows you to repaint the grandson red and send it to the right subtree by making a small right turn 3-7, and don't ask why, just trust and check that the black height has stabilized:
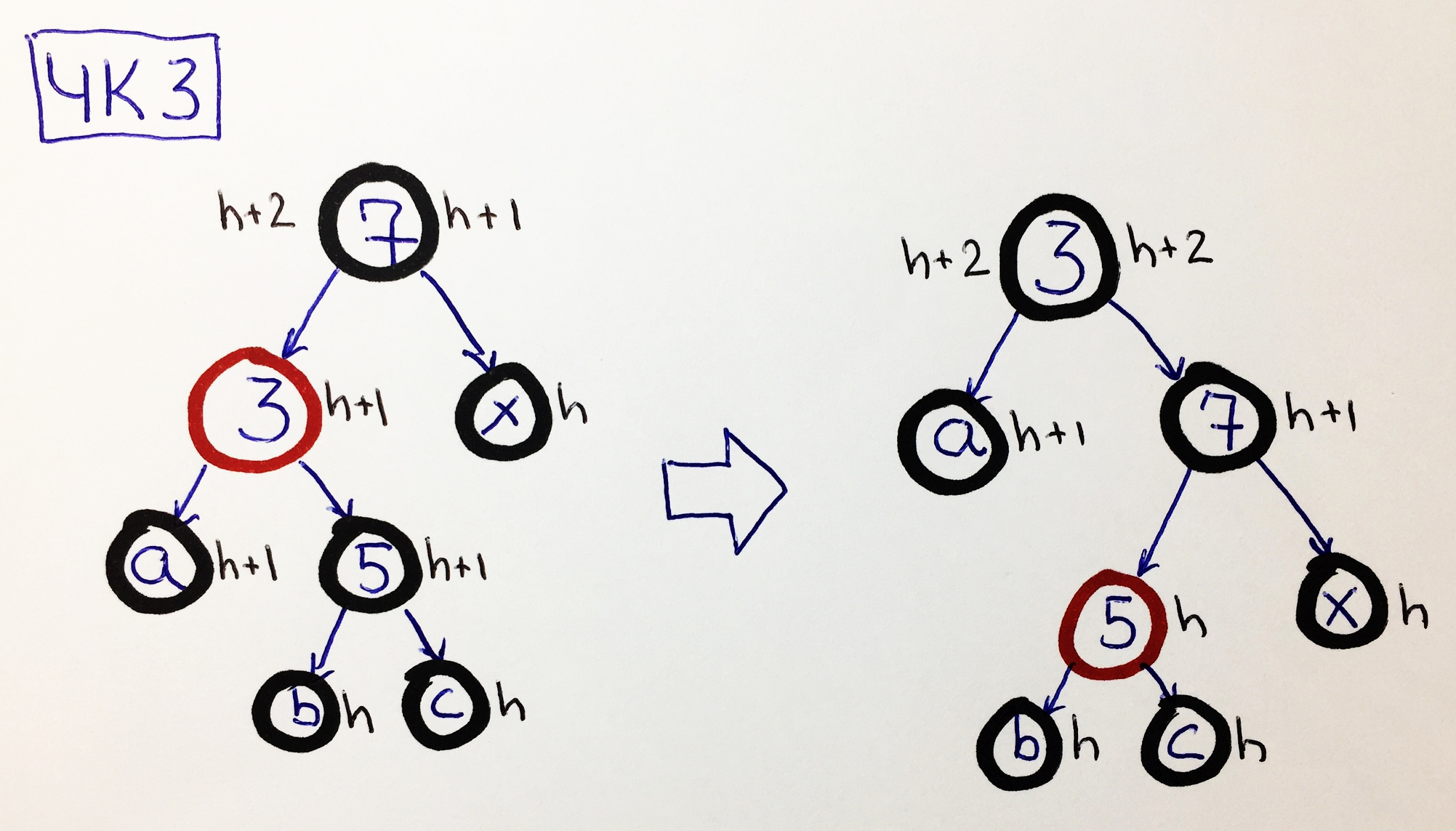
Note that the red node 5 does not increase the black height.
CHK4 - the parent is black, the left son is red, the right grandson has a red great-grandson
Further into the red forest, there are more black firewoods, and there are fewer red ones, namely, by recoloring the red nodes, it is possible to stabilize the black height.

In this case, you need to make a large left turn, which consists of two small turns 5-3 and 5-7. Node b changed its color from red to black and thus increased its height by 1. Make sure that the black height has stabilized.
HCH5 - the parent is black, the left son is black with the right red grandson.
Fewer and fewer red elements in our subtree, repaint the last red grandson black and make a big left turn, as in the previous case.

Check that the black height of the subtree has stabilized.
HCH6 - the parent is black, the left son is black, his grandchildren are also black
And then came the moment when the red wood ran out. There is nothing to do, you have to paint the black node red and thus align the black height of node 7, but not by increasing the black height of the right subtree, but by decreasing the black height of the left subtree. As a result, the black height of our entire structure will decrease by 1 and we must recursively call balancing to the forefathers.

Deletion example with balancing and recursion
We looked at all 6 cases of black height balancing after removing an element from the red-black tree. To get a better feel for how this all works, let's continue removing node 30 from the original tree.
The first step is simply to delete node 30. The
second step is to launch balancing on its parent - node 25.
There is a case of HH6:

The height of node 25 has been stabilized with grief in half.
The third step is balancing at the grandfather's level - for node 20.
To make it more fun and clearer , let's draw the whole tree before and after balancing. This is the case for HK4:

Notice how the red-black tree changed after balancing, some of the elements from the left subtree moved to the right, the height stabilized, the element was removed, everyone is happy!
Removing items from a red-black tree is one of the most difficult operations when working with binary search trees. In the course " Algorithms and Data Structures " we consider not only binary search trees, but also many other interesting algorithms, for more details see the course program.
