Mathematicians have long been trying to get used to the fact that some problems, in principle, cannot be solved.

We like to say that anything is possible. In Jaster Norton's book "Cute and the Magic Booth", the king refuses to inform Milo that his goal is unattainable, because "a lot becomes possible if you don't know that it's impossible" [ though these are the words of other characters in the book / approx. transl. ]. But in the real world, some things are really impossible, and we can prove it with mathematics.
People use the term "impossible" in many different ways. He can describe just the unlikely things, such as finding two identical decks of shuffled cards. It can describe tasks that are nearly impossible due to lack of time, space, or resources, such as rewriting the entire Library of Congress by hand. Devices such as perpetual motion machines are physically impossible, since their existence would contradict our understanding of physics.
Mathematical impossibility is different. We start with unambiguous assumptions, and using mathematical reasoning and logic, we conclude that some outcomes are impossible. No amount of luck, persistence, time, or skill will make the task doable. The history of mathematics is replete with proofs of impossibility. Many of these are considered to be the most remarkable results of mathematics. But it was not always so.
The punishment for, perhaps the very first proof of impossibility, was strict. Historians believe that in the 5th century BC. Hippasus of Metapont, a follower of Pythagoras, discovered that it was impossible to find a line segment that could measure both the side length and the diagonal length of a regular pentagon. Today we say that the length of the diagonal of a regular pentagon with side length 1 is the golden ratio, ϕ = 1/2 (1 + √5) - is an irrational number. The discovery of Hippasus was a challenge to the Pythagorean credo, "everything is number", therefore legends say that Hippasus was either drowned in the sea, or simply expelled from the ranks of the Pythagoreans.
More than a century later, Euclid elevated the line and the circle as fundamental curves of geometry. Subsequently, many generations of geometers drew anything - dividing angles, drawing perpendiculars, and so on - only with the help of compasses and a ruler. However, certain structures, which seemed simple, puzzled Greek geometers, acquired a mythical status as a result, and annoyed mathematicians for over 2000 years. These are the problems of dividing an arbitrary angle into three parts, constructing the side of a cube, the volume of which is twice the volume of the given one, constructing all regular polygons, and also constructing a square with an area equal to the area of a given circle.
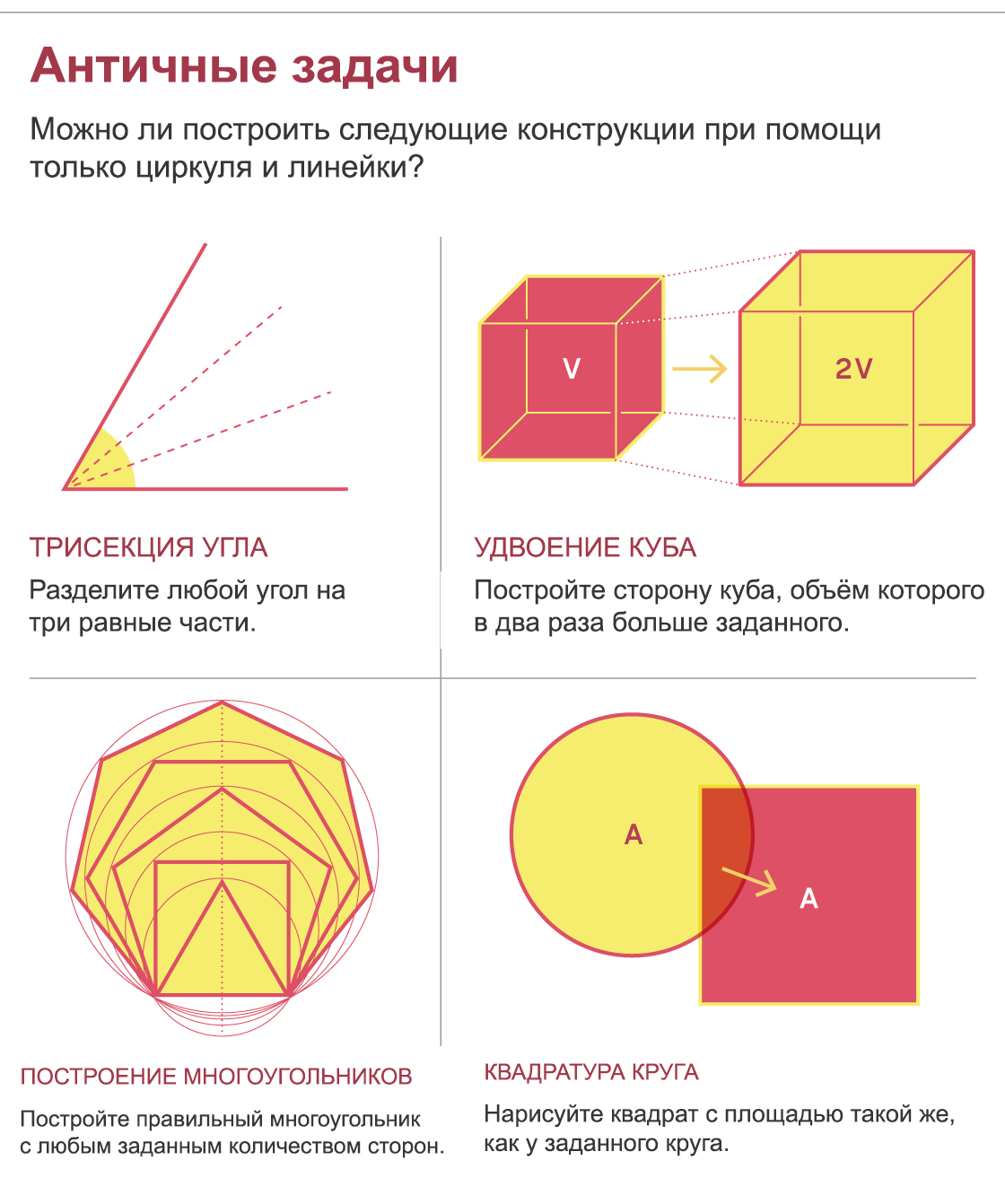
Although these problems are geometric in nature, the proof that they cannot be solved is not. New mathematics was required to demonstrate the impossibility of solving them.
In the 17th century, René Descartes made a fundamental discovery: if we limit ourselves to only compasses and a ruler, we cannot draw segments of any length. If we start with a line of length 1, we can only construct lines whose length can be expressed using integers, addition, subtraction, multiplication, division and square root (like the golden ratio).
Therefore, one of the strategies for finding a proof of the impossibility of solving a geometric problem - that is, that a certain object cannot be constructed - will be to show that the length of a certain segment of the final figure cannot be expressed in this way. But in order to show this rigorously, the then emerging algebra was required.
Two centuries later, Descartes' compatriot, Pierre Laurent Vanzel , used polynomials (sums of coefficients and variables raised to a power) and their roots (variables that make the polynomial equal to zero) to attack these classical problems. For example, in the problem of doubling a cube, the side of a cube with a volume twice that of a unit cube should be equal to... This is the root of the polynomial x 3 -2 because...
In 1837 Wanzel proved that in order for a segment to be constructed using a compass and a ruler, its length must be the root of a polynomial that cannot be factorized, and whose power (the highest power of the variable) is a power of two. For example, the golden ratio is the root of the second degree polynomial x 2 - x - 1. But x 3 -2 is a third degree polynomial, soyou can't build. So Wanzel concluded that doubling the cube was impossible.
In a similar way, he proved that it is impossible to use classical tools to trisect any angle or construct certain regular polygons - for example, a seven-sided one. Interestingly, all three proofs of impossibilities were posted on the same page. As Isaac Newton and Albert Einstein had their annus mirabilis (years of miracles), this situation can be called pagina mirabilis - a page of miracles.
Proving the impossibility of the remaining problem, squaring the circle, required something new. In 1882 Ferdinand von Lindemannproved the key point - that the number π cannot be constructed - by proving its transcendence, that is, that it is not a root of any polynomial.
These classic problems can be attributed to a bad reputation and considered to be sirens that lured mathematicians to crash on the sharp rocks of impossibility. But I consider them muses that have inspired generations of creative thinkers.
The same applies to the newer impossible task arising from such a simple act as crossing a bridge. Imagine that you live in Pittsburgh, the “city of bridges,” like many of my students. Any adventurous cyclist might wonder if starting a ride from home can cross each of the 22 bridges that cross Pittsburgh's major rivers exactly once and return home.
In 1735, the Prussian mayor set a similar task for Leonard Euler, only for Königsberg (now Kaliningrad). Seven bridges of this city connect the three banks of the river and the island. At first, Euler dismissed this problem as not a mathematical one: "Solutions of this kind have little to do with mathematics, and I do not understand why you expect a mathematician to give it to you and not someone else."
However, soon Euler proved the impossibility of solving this problem, and in the process created a new area of mathematics, which he called the geometry of arrangements - what we today call topology. He realized that the specific details - the exact locations of bridges, the shape of the parcels of land, etc. - were not important. Only their connections were important. Later, mathematicians refined Euler's formulations using what we call graphs today. The idea of connectivity is at the core of learning about social media, the internet, epidemiology, linguistics, route planning, and more.
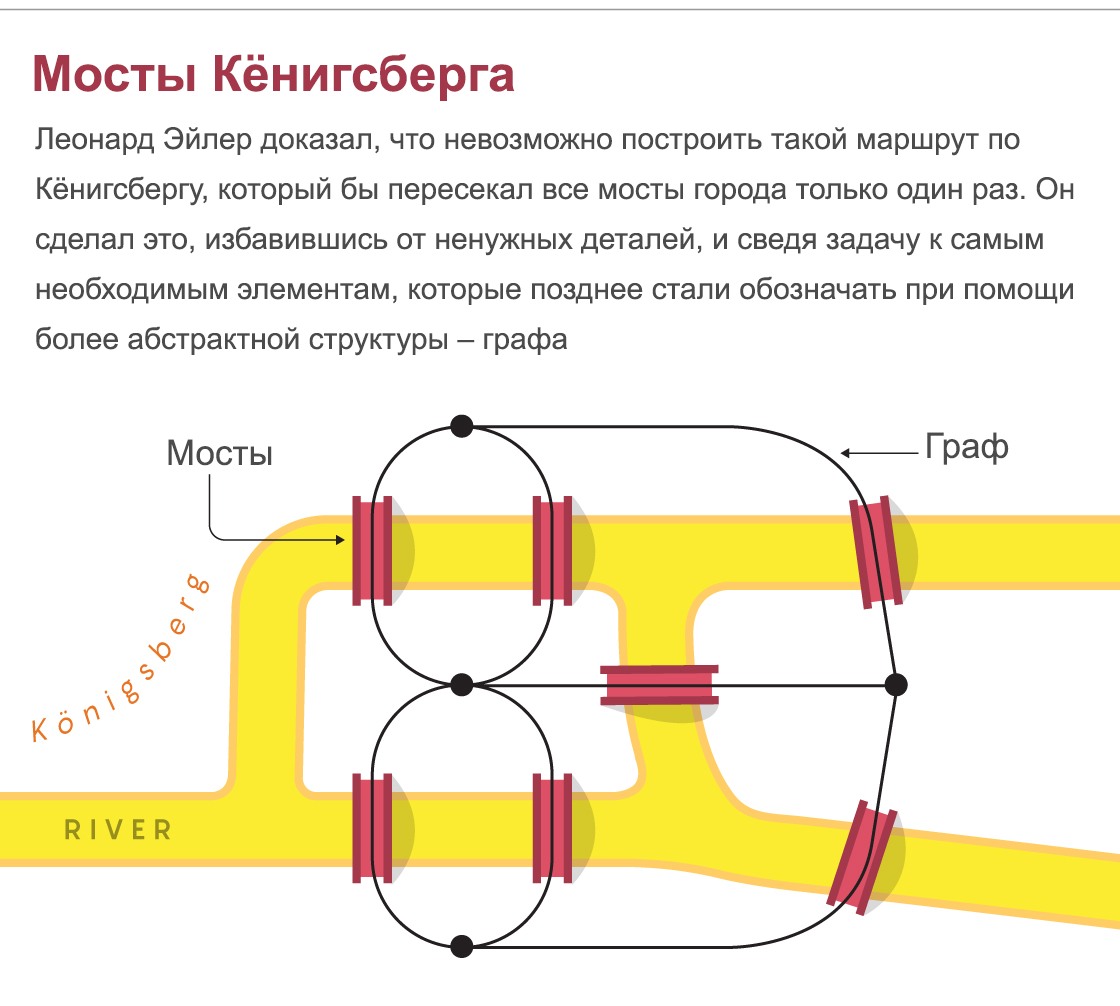
Königsberg Bridges: Leonard Euler proved that it is impossible to build a route along Königsberg that would cross all the bridges of the city only once. He did this by getting rid of unnecessary details, and reducing the task to the most necessary elements, which later began to be designated using a more abstract structure - the graph.
Euler's proof was surprisingly simple. He reasoned that every time we come in and then leave a particular piece of land, we must eliminate two bridges. Therefore, there must be an even number of bridges for each piece of land. But since an odd number of bridges led to each section of Königsberg, it was impossible to build such a route. Likewise, the three bridges leading to Gers Island on the Allegheny River in Pittsburgh make it impossible to build the desired cycle route.
As this problem shows, impossibilities are not limited to abstract mathematics. They can have real-world consequences - sometimes even political ones.
Recently, mathematicians have turned to the concept of gerrymendering . In the United States, after each census, the states must redo the constituencies. But sometimes the ruling party rewrites their boundaries in ridiculous ways to maximize their political power.
Many states have a requirement for “compact” districts that does not have a strict mathematical definition. In 1991 Daniel Paulsby and Robert Popper proposed 4πA / P 2as a way to measure the compactness of the area A and the perimeter P. These values range from 1 for a round parish to almost zero for deformed counties with a long perimeter.
Meanwhile, Nicholas Stephanopoulos and Eric McGee introduced the “performance gap” in 2014 as a measure of the political integrity of a district change plan. Two different gerrymandering strategies are either for the opposition in the constituency to have less than 50% of the vote, or around 100%. Each of these tactics makes the opposition lose votes by losing the right candidates or wasting votes on those who don't. The efficiency gap describes the relative number of lost votes.
Both of these measures are useful for recognizing gerrymandering. But in 2018 Boris Alekseev and Dustin Mixonproved that "sometimes small efficiency gaps can be achieved with oddly shaped counties." That is, it is mathematically impossible to always draw counties to satisfy both Paulsby-Popper's requirements and the integrity of the efficiency gap.
However, detecting and preventing surreptitious gerrymandering techniques is a rapidly growing field that attracts many talented research efforts. As with the problems of antiquity or the problem of Königsberg bridges, I am sure the gerrymendering problem will inspire creativity and contribute to the development of mathematics.