This week (September 16-26) in St. Petersburg (virtually) started the 61st International Mathematical Olympiad , 622 schoolchildren from 114 countries take part in it.
The first such Olympiad was held in 1959 in Romania, and then representatives of only seven countries took part in it.
Russia is represented by a team of six high school students.
Schoolchildren are given 2 days of 4.5 hours to solve 6 problems. While the results are being evaluated, I suggest you try to solve the problems and discuss in the comments.
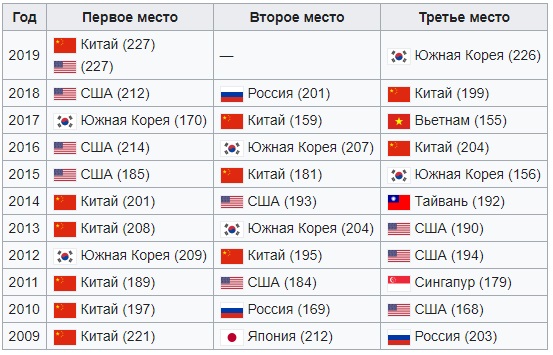
Results of past years.
Problem 1
Inside the convex quadrilateral ABCD, there is a point P such that the equalities
∠PAD: ∠PBA: ∠DPA = 1: 2: 3 = ∠CBP: ∠BAP: ∠BPC hold.
Prove that the following three straight lines intersect at one point: the inner bisectors of the angles ∠ADP and ∠PCB and the midpoint perpendicular to the segment AB.
Problem 2
Given real numbers a, b, c, d such that a> b> c> d> 0 and a + b + c + d = 1.
Prove that
(a + 2b + 3c + 4d) a a b b c c d d <1.
Problem 3
There are 4n pebbles with masses 1, 2, 3, ..., 4n . Each of the pebbles is colored in one of n colors, and there are 4 pebbles of each color.
Prove that the stones can be divided into two heaps of equal total weight so that each heap contains two stones of each color.
Task 4
An integer n> 1 is given . There are n 2 funicular stations on the slope at different heights. Each of the two funicular companies A and B owns k lifts. Each lift carries out a regular direct transfer from one of the stations to another, higher station. The k transfers of company A start at k different stations; they also end at k different stations; with a transfer that starts above and ends above. The same conditions are met for company B. We will say that two stations are connectedfunicular company, if you can get from the lower station to the upper one using one or more transfers of this company (other transfers between stations are prohibited). Find the smallest k for which there are known to be two stations connected by both companies.
Problem 5
There are n> 1 cards, each of which contains a positive integer.
It turned out that for any two cards the arithmetic mean of the numbers written on them is equal to the geometric mean of the numbers written on the cards of a certain set consisting of one or more cards. For which n does it follow that all the numbers written on the cards are equal?
Problem 6
Prove that there exists a positive constant c for which the following statement holds:
Let S be a set of n> 1 points of the plane in which the distance between any two points is at least 1. Then there is a line ℓ separating the set S such that the distance from any points S to ℓ are at least cn −1/3 .
(A straight line ℓ separates the set of points S if it intersects some segment whose ends belong to S.)
Remark. Weaker results with cn −1/3 replaced by cn −α can be estimated depending on the value of the constant α> 1/3 .