👨🏾‍🏭 🤨 🔅 How to draw a star (and more) in polar coordinates 💆🏽 🗾 👨🏿‍🍳

The question of the formula for a polygon in polar coordinates regularly arises on thematic resources - and just as regularly remains without a clear answer. In the best case, a solution comes across through the remainder function - which is not "clean" from a mathematical point of view, since it does not allow performing analytical transformations on the function. Apparently, real mathematicians are too busy solving problems of the millennium and looking for a simple proof of Fermat's theorem to pay attention to such banal problems. Fortunately, in this matter, imagination is more important than knowledge, and to solve this problem you do not need to be a professor of topological sciences - school-level knowledge is enough.

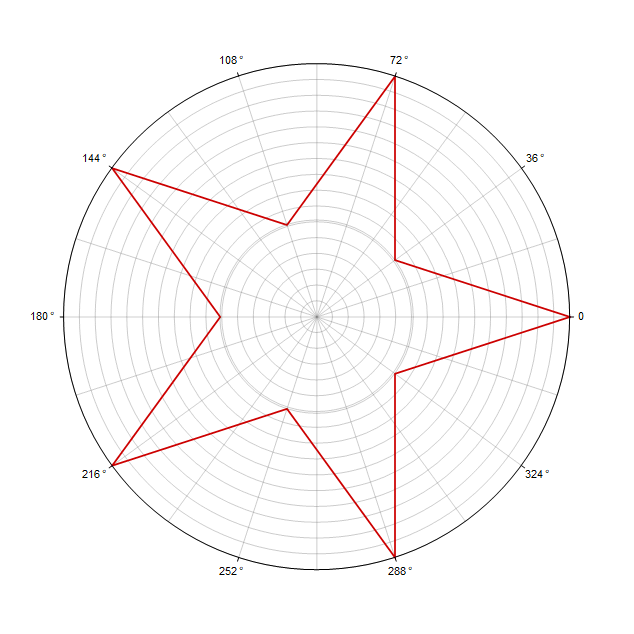
The formula for an equilateral polygon in polar coordinates looks very simple

ρ = \frac{\cos (\frac{2 \sin^{- 1} (k) + π m}{2 n})}{\cos (\frac{2 \sin^{- 1} (k \cos (n ϕ)) + π m}{2 n})}

$\rho = \frac{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}(k \cos (n \phi ))+\pi m}{2 n}\right)}$

and has the following parameters:

ϕ

$\phi$ - angle;

n

$n$ - the number of convex vertices;

m

$m$ - determines how many vertices the sides will lie on one straight line. Negative values are also permissible for it - the sign will determine in which direction the star will bend;

k

$k$ - rigidity - at

k = 0

$k=0$ we get a circle regardless of other parameters, for

k = 1

$k=1$ - a polygon with straight lines, at intermediate values from

0

$0$ before

1

$1$ - intermediate figures between a circle and a polygon.

With this formula, you can draw a star in two ways:

1)

n = 5, m = 3

$n=5, m=3$

n = 5 / 4, m = 0

$n=5/4,m=0$ ... In this case, you need to make two turns instead of one:

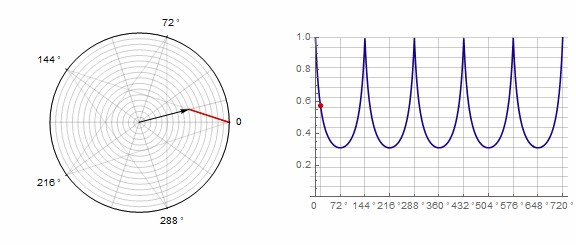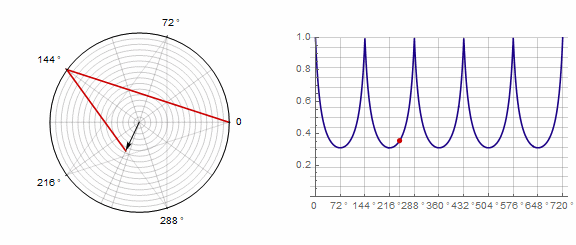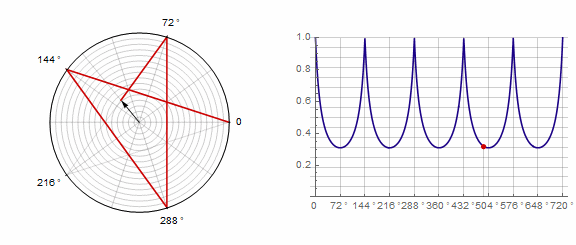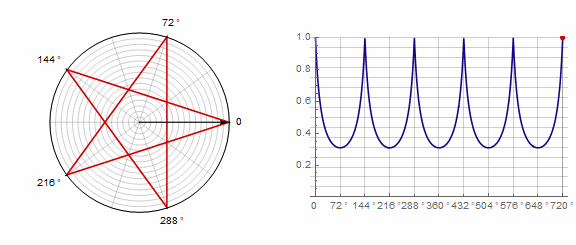
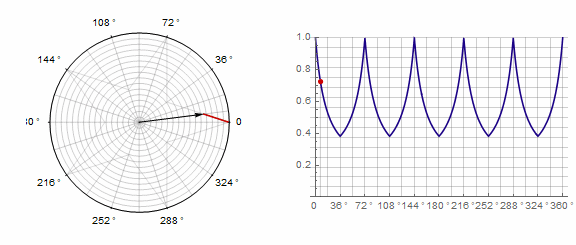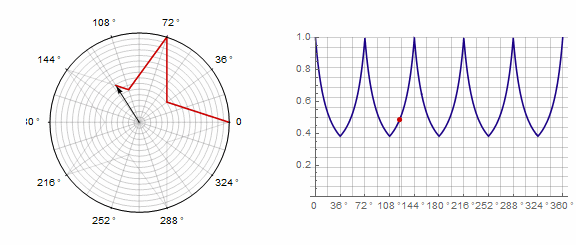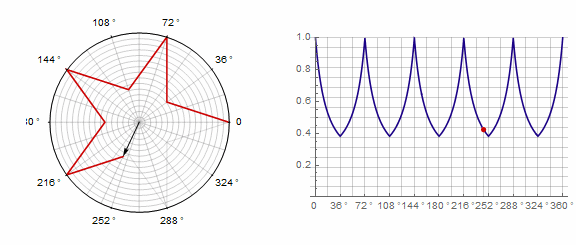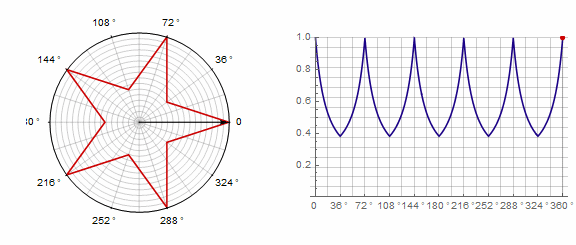
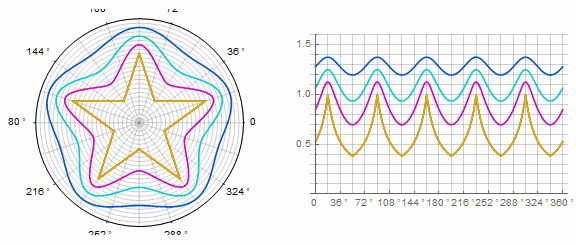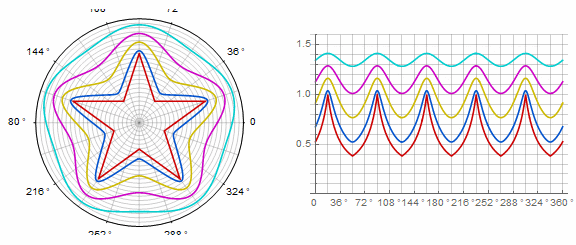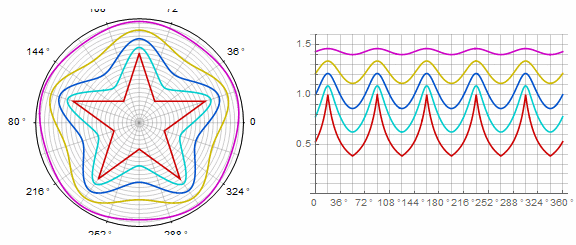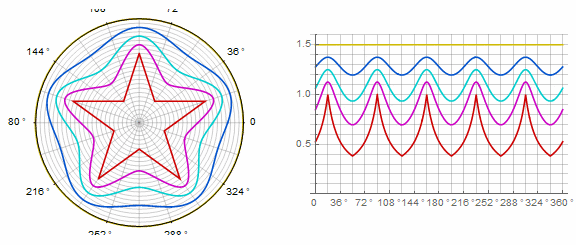
Parameter

m

$m$ affects the polygon as follows (here it changes from -1 to 5):

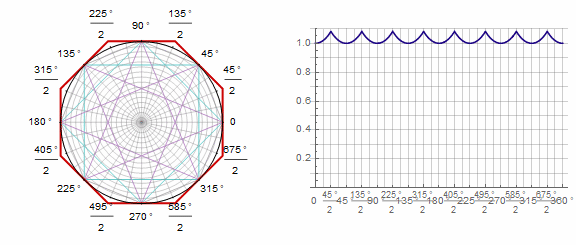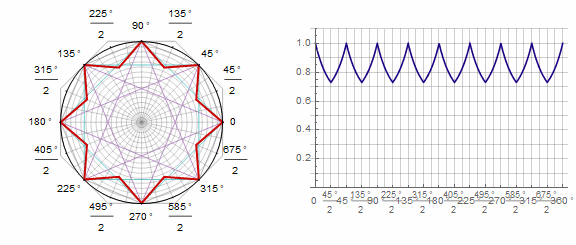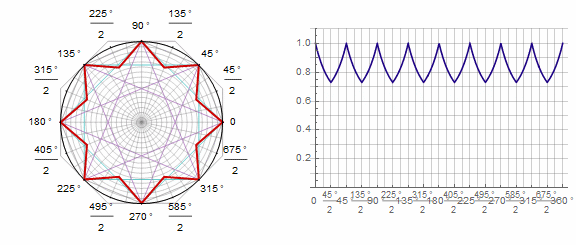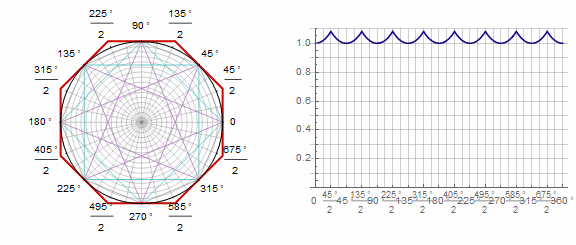
Parameter

k

$k$ in animation:

Complex form and modifications

You can rewrite the original formula in a complex form, and, despite the presence of imaginary units in it, the value of the radius will still remain valid:

ρ = \frac{4^{1 / n} {(\sqrt{1 - k^{2}} + i k)}^{- 1 / n} (1 + {(\sqrt{1 - k^{2}} + i k)}^{2 / n} e^{\frac{i π m}{n}}) {(\sqrt{1 - k^{2} \cos^{2} (n ϕ)} + i k \cos (n ϕ))}^{1 / n}}{4^{1 / n} + e^{\frac{i π m}{n}} {(2 \sqrt{1 - k^{2} \cos^{2} (n ϕ)} + 2 i k \cos (n ϕ))}^{2 / n}}

$\small\rho = \frac{4^{1/n} \left(\sqrt{1-k^2}+i k\right)^{-1/n} \left(1+\left(\sqrt{1-k^2}+i k\right)^{2/n} e^{\frac{i \pi m}{n}}\right) \left(\sqrt{1-k^2 \cos ^2(n \phi )}+i k \cos (n \phi )\right)^{1/n}}{4^{1/n}+e^{\frac{i \pi m}{n}} \left(2 \sqrt{1-k^2 \cos ^2(n \phi )}+2 i k \cos (n \phi )\right)^{2/n}}$

At first glance, this may seem pointless, since the formula has become a little more cumbersome - but don't jump to conclusions. First, there is no arcsine in it, which completely changes the mathematical meaning of the formula and allows you to look differently at the construction of a stellated polygon. Secondly, it can also be used to obtain compact formulas for special cases, for example

\frac{i^{t} {(i^{n t})}^{1 / n}}{1 + {(i^{n t})}^{2 / n}}

$\frac{i^t \left(i^{n t}\right)^{1/n}}{1+\left(i^{n t}\right)^{2/n}}$ ... Thirdly (and most interestingly), it can be creatively modified and obtained other, unexpected forms. In order for the appearance of a possible imaginary component in the radius not to cause ambiguity in the calculation, it can be immediately reduced to Cartesian coordinates by multiplying by

e^{i ϕ}

$e^{i \phi }$ ... Here are examples of some of the modifications:

\frac{(- 1)^{2 / 3} e^{i ϕ} {(i \cos (3 ϕ) + \sqrt{\sin^{2} (3 ϕ)})}^{1 / 3}}{(- 1)^{2 / 3} + 2^{2 / 3} {(i \cos (3 ϕ) + \sqrt{\sin^{2} (3 ϕ)})}^{2 / 3}}

$\frac{(-1)^{2/3} e^{i \phi } \left(i \cos (3 \phi )+\sqrt{\sin ^2(3 \phi )}\right)^{1/3}} {(-1)^{2/3}+2^{2/3} \left(i \cos (3 \phi )+\sqrt{\sin ^2(3 \phi )}\right)^{2/3}}$

\frac{e^{i ϕ} \sqrt{i \cos (2 ϕ) + \sqrt{\sin^{2} (2 ϕ)}}}{e^{i / 2} + \sqrt{2} {(i \cos (2 ϕ) + \sqrt{\sin^{2} (2 ϕ)})}^{3 / 2}}

$\frac{e^{i \phi } \sqrt{i \cos (2 \phi )+\sqrt{\sin ^2(2 \phi )}}}{e^{i/2}+\sqrt{2} \left(i \cos (2 \phi )+\sqrt{\sin ^2(2 \phi )}\right)^{3/2}}$

\frac{e^{\frac{1}{4} i (4 ϕ + π)}}{2 \sqrt{(- 1)^{1 / 4} \cos (2 ϕ) + \sqrt{\sin^{2} (2 ϕ)}} - 1 - i}

$\frac{e^{\frac{1}{4} i (4 \phi +\pi )}}{2 \sqrt{(-1)^{1/4} \cos (2 \phi )+\sqrt{\sin ^2(2 \phi )}}-1-i}$

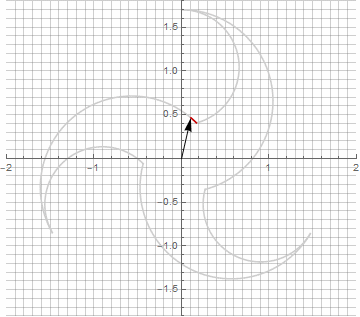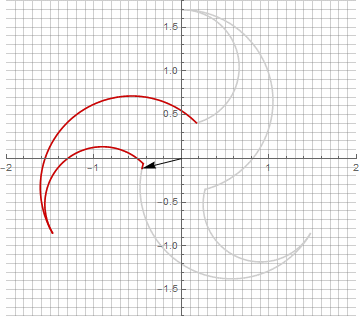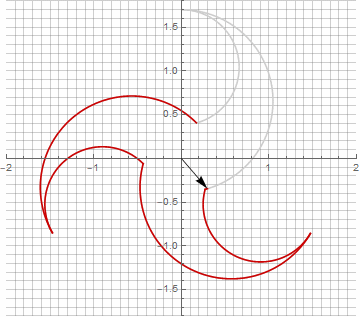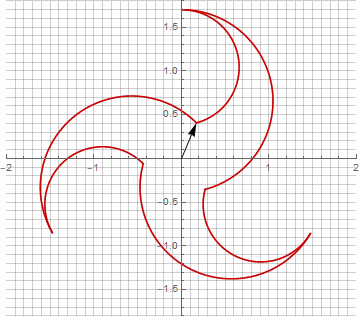
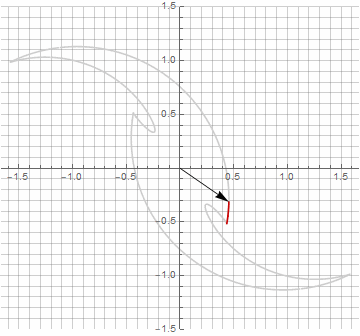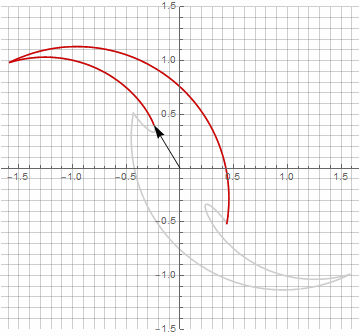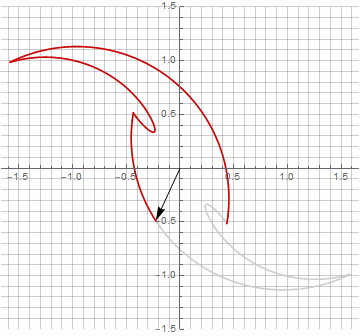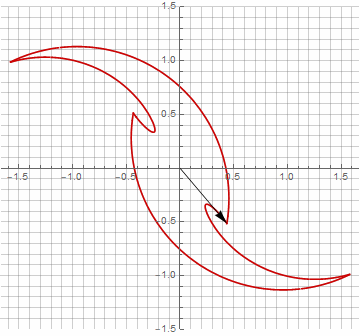
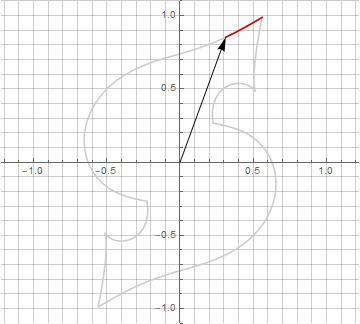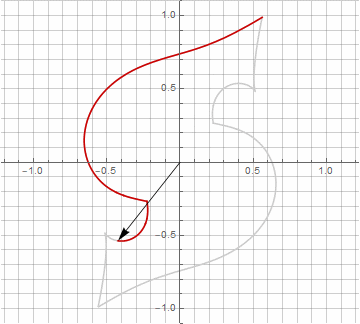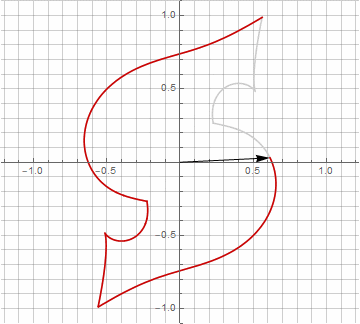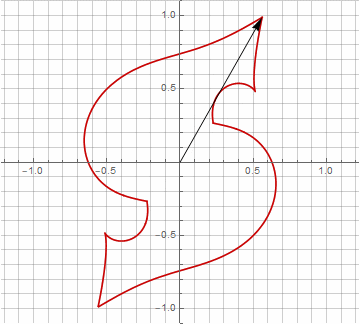
As you probably noticed, the rotation of the vector has ceased to be uniform - and precisely because of the appearance of the imaginary component in the radius.

Quads and stuff

Our formula has a wonderful special case - a square, the formula for which can be written as

ρ = \frac{2}{\sqrt{2 + \sqrt{2 + 2 \cos (4 ϕ)}}}

$\rho = \frac{2}{\sqrt{2+\sqrt{2+2 \cos (4 \phi )}}}$

ρ = \sqrt{\frac{2}{1 + \sqrt{1 - \sin^{2} (2 ϕ)}}}

$\rho = \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 \phi )}}}$

(choose which one you like best).

In a slightly more developed case, you can define intermediate figures between a circle and a square through a point

(k, k)

$(k,k)$ on surface

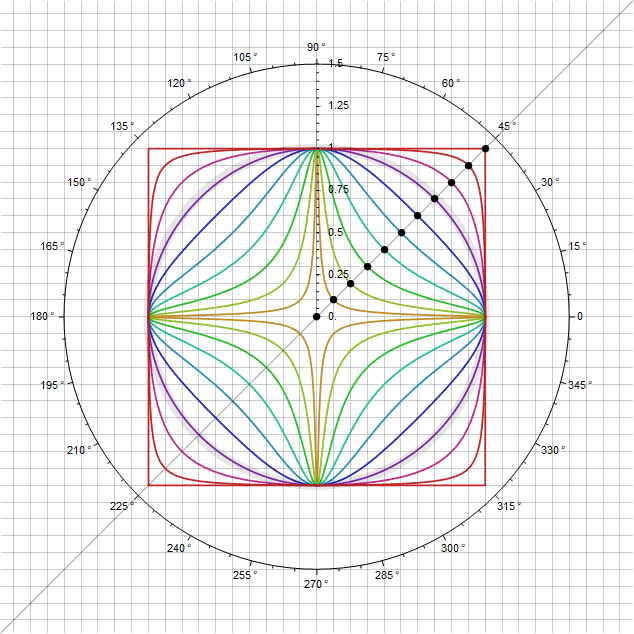
ρ = \sqrt{\frac{2}{1 + \sqrt{1 - \frac{(2 k^{2} - 1) \sin^{2} (2 ϕ)}{k^{4}}}}}

$\rho = \sqrt{\frac{2}{1+\sqrt{1-\frac{\left(2 k^2-1\right) \sin ^2(2 \phi )}{k^4}}}}$

You can also add variation to these shapes while maintaining the condition that they pass through the point

(k, k)

$(k,k)$ - modulating directly the parameter itself

k

$k$ depending on the angle so that when passing through the diagonal, its multiplier is equal to one. For example, substituting instead

k

$k$ function

\frac{k}{1 - z \cos^{2} (2 ϕ)}

$\frac{k}{1-z \cos ^2(2 \phi )}$ , we will get an additional parameter

z

$z$ with which additional bends can be adjusted. In particular, for

z = 1 / 4

$z=1/4$ you get the following:

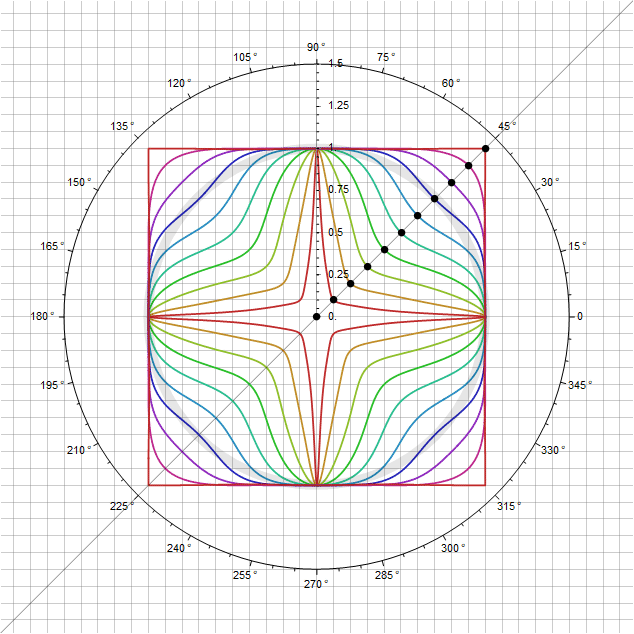
In an even more expanded case, you can define not just a square, but a rectangle, and still in polar coordinates:

ρ = \sqrt{\frac{4 a^{2} b^{2}}{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2}) (\sqrt{1 - \frac{4 a^{2} b^{2} k \sin^{2} (2 ϕ)}{{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2})}^{2}}} + 1)}}

$\rho = \sqrt{\frac{4 a^2 b^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right) \left(\sqrt{1-\frac{4 a^2 b^2 k \sin ^2(2 \phi )}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right)^2}}+1\right)}}$

And even calculate its area (via elliptic integrals):

S = 4 a b \frac{(k - 1) K (k) + E (k)}{k}

$S=4 a b\frac{(k-1) K(k)+E(k)}{k}$

Note

k

$k$ (

0

$0$

1

$1$ ) ,

π a b

$\pi a b$

4 a b

$4 a b$ .

This will allow making profiles with a transition from a circle to a rectangle with a controlled section area. Here the area is constant:

And here the area expands exponentially:

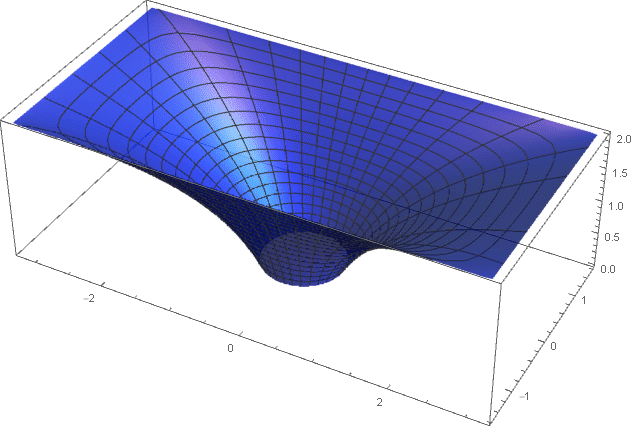
Go to Cartesian coordinates

Any formula in polar coordinates can be expressed through an equation in Cartesian coordinates, and in at least two ways - depending on which the form of the gradient on the border of the figure will change. To do this, it is enough to calculate the angle through the arctangent of the coordinates and bring the formula to a constant through the radius vector by subtracting

0 = \sqrt{x^{2} + y^{2}} - \frac{\cos (\frac{2 \sin^{- 1} (k) + π m}{2 n})}{\cos (\frac{2 \sin^{- 1} (k \cos (n \tan^{- 1} (x, y))) + π m}{2 n})}

$0=\sqrt{x^2+y^2}-\frac{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}\left(k \cos \left(n \tan ^{-1}(x,y)\right)\right)+\pi m}{2 n}\right)}$

or division

1 = \frac{\sqrt{x^{2} + y^{2}} \cos (\frac{2 \sin^{- 1} (k \cos (n \tan^{- 1} (x, y))) + π m}{2 n})}{\cos (\frac{2 \sin^{- 1} (k) + π m}{2 n})}

$1=\frac{\sqrt{x^2+y^2} \cos \left(\frac{2 \sin ^{-1}\left(k \cos \left(n \tan ^{-1}(x,y)\right)\right)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}$

The second option is preferable because it gives straight gradients along the sides of the polygon.

Note

, (0,0) - — , , (

- \cos (\frac{2 \sin^{- 1} (k) + π m}{2 n}) \sec (\frac{2 \sin^{- 1} (k \cos (\frac{π n}{2})) + π m}{2 n})

$-\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right) \sec \left(\frac{2 \sin ^{-1}\left(k \cos \left(\frac{\pi n}{2}\right)\right)+\pi m}{2 n}\right)$ ).

\cos (n \tan^{- 1} (x, y))

$\cos \left(n \tan ^{-1}(x,y)\right)$

\frac{(x + i y)^{n} + (x - i y)^{n}}{2 {(x^{2} + y^{2})}^{n / 2}}

$\frac{(x+i y)^n+(x-i y)^n}{2 \left(x^2+y^2\right)^{n/2}}$ , A034839.

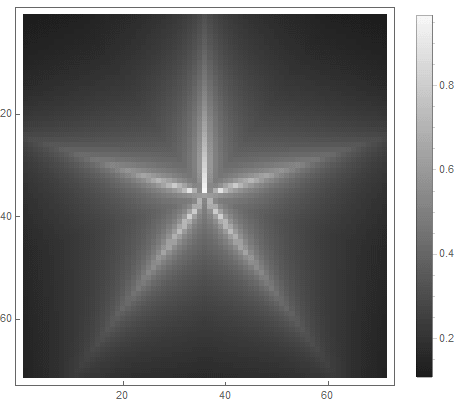
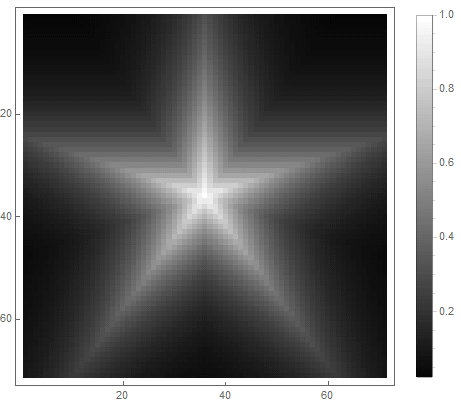
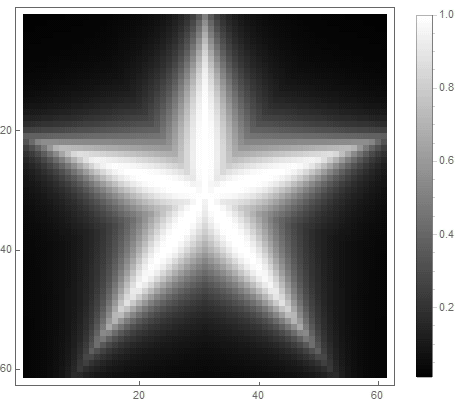
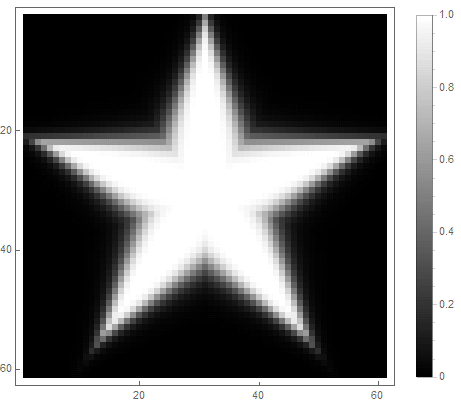
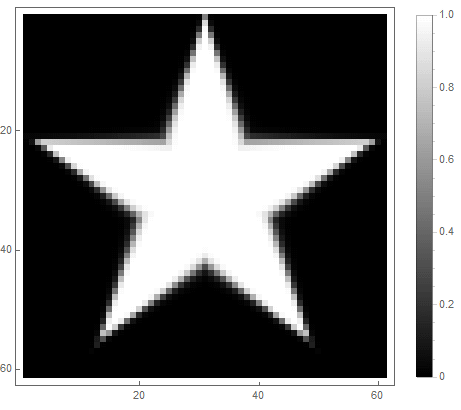
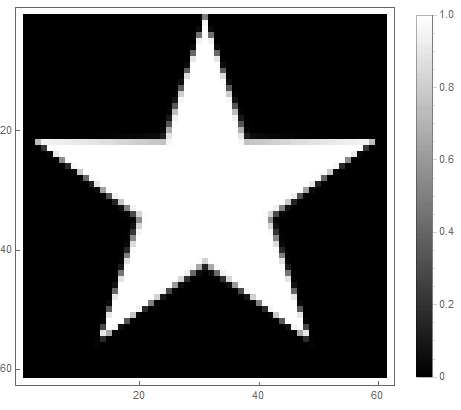
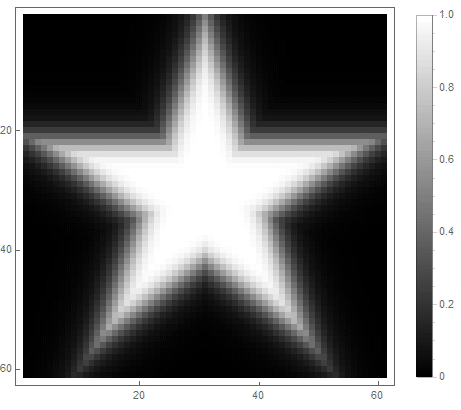
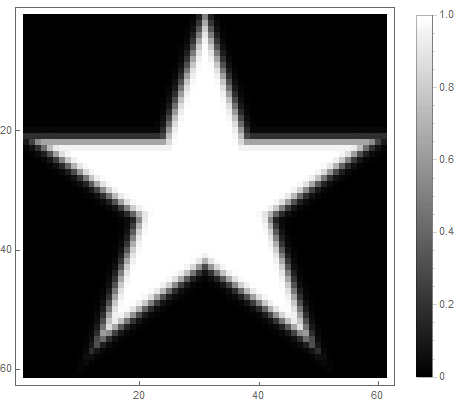
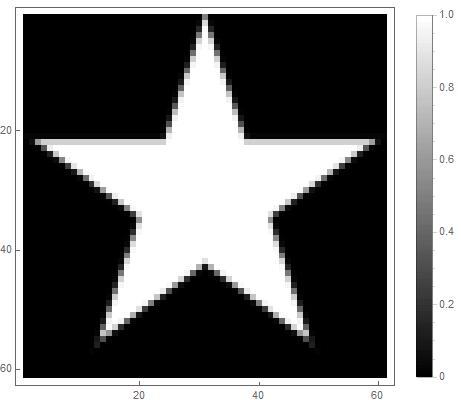
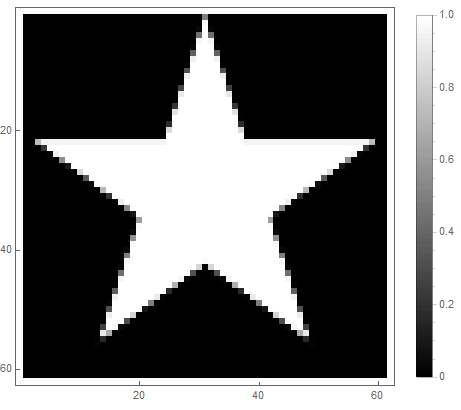
The value of the formula from the right side of the equation (in the 2nd case) will change from

0

$0$ before

1

$1$ if point

(x, y)

$(x,y)$ gets inside the figure, and from

1

$1$ ad infinitum - if not. By choosing different functions to convert it to brightness, you can get different rasterization options. For the exponent (

e^{- x - 1}

$e^{-x-1}$ for the first and

e^{- x}

$e^{-x}$ for the second option) we get

or, if with saturation

Classic low pass filter can be used

\frac{1}{1 + x^{p}}

$\frac{1}{1+x^p}$ , in which

p

$p$ - the order of the filter, which determines the degree of attenuation.

For the first option:

And for the second:

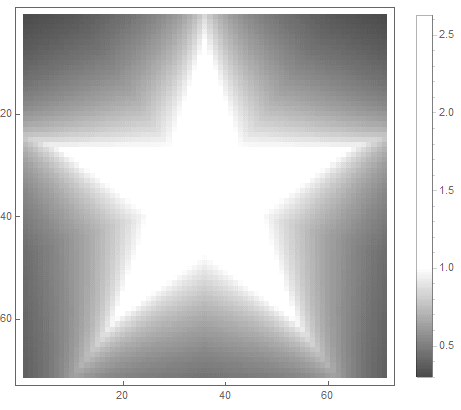
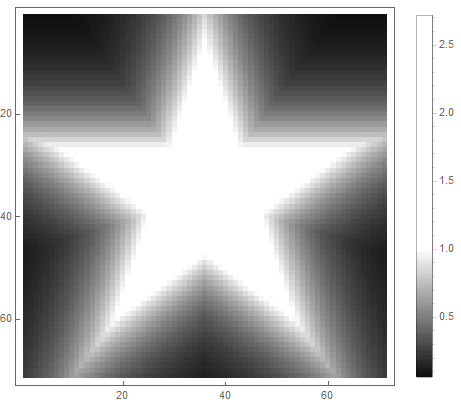
You can also use a piecewise continuous function by explicitly setting the interpolation boundaries.

In addition to rasterization as such, you can also set deformations - for example, squeeze a checkerboard into a circle:

Or even pull it over a sphere:

Formula

x = \frac{u}{\sqrt{\frac{2}{1 + | \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |}}}

$x=\frac{u}{\sqrt{\frac{2}{1+ \left| \frac{u^2-v^2}{u^2+v^2} \right|}}}$

y = \frac{v}{\sqrt{1 + \frac{2}{| \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |}}}

$y=\frac{v}{\sqrt{1+\frac{2}{\left| \frac{u^2-v^2}{u^2+v^2}\right| }}}$

z = \sqrt{1 - \frac{1}{2} u^{2} (1 + | \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |) - \frac{1}{2} v^{2} (1 + | \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |)}

$z=\sqrt{1-\frac{1}{2} u^2 \left(1+\left| \frac{u^2-v^2}{u^2+v^2}\right|\right)-\frac{1}{2} v^2 \left(1+\left| \frac{u^2-v^2}{u^2+v^2}\right|\right)}$

Appendix: how the formula was derived

The classical style of storytelling in mathematical texts consists of the alternation of lemmas / theorems and their proofs - as if the provable statements appeared in the author's head by a revelation from above. And although there is some truth in this, more often the appearance of formulas is preceded by some research work, the description of which can give a greater understanding of their meaning than formal proof; and the fidelity of the statements, in turn, can be traced through the fidelity of the steps that led to them.

So here too - if the article began with a formula in a complex form, then its appearance would be non-obvious and counter-intuitive, and the declared properties would require additional proofs. But in the trigonometric form of recording, the history of its appearance is quite possible to trace.

1) we start with the simplest case - the task of drawing a straight line in polar coordinates. To do this, you need to solve the equation

r \cos (ϕ) = 1

$r \cos (\phi )=1$ whose solution is obvious

r \to \sec (ϕ)

$r\to \sec (\phi )$ ...

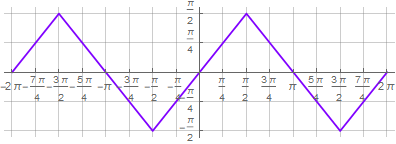
2) further, the secant argument needs to be "looped" to provide kinks in a straight line. It is at this stage that other solutions use a "dirty hack" in the form of a division remainder. It also uses sequential taking of the direct and inverse sine function -

\sin^{- 1} (\sin (ϕ))

$\sin ^{-1}(\sin (\phi ))$

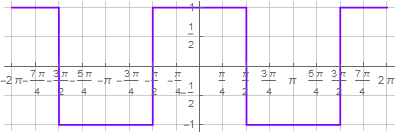
This approach allows you to perform standard mathematical operations on the resulting formula,

\frac{\partial \sin^{- 1} (\sin (ϕ))}{\partial ϕ} = \frac{\cos (ϕ)}{\sqrt{1 - \sin^{2} (ϕ)}}

$\frac{\partial \sin ^{-1}(\sin (\phi ))}{\partial \phi }=\frac{\cos (\phi )}{\sqrt{1-\sin ^2(\phi )}}$

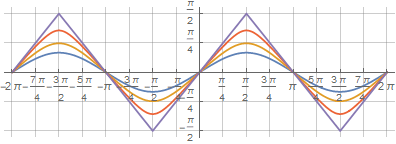
Thanks to the same notation, you can simplify the square function in polar coordinates to a more aesthetic look, using the complex representation of trigonometric functions. In Wolfram Mathematica, this can be done using the TrigToExp and ExpToTrig functions:

The code

Sec[1/2 ArcSin[k Sin[2 \[Phi]]]]^2//TrigToExp//ExpToTrig//Sqrt[#]&//FullSimplify

↓

\frac{2}{\sqrt{2 + 2 \sqrt{1 - k^{2} \sin^{2} (2 ϕ)}}}

$\frac{2}{\sqrt{2+2 \sqrt{1-k^2 \sin ^2(2 \phi )}}}$

Thanks to the same recording, you can get smooth intermediate figures between a circle and a square using an additional multiplier

k

$k$ due to which the arcsine argument falls short of one -

\sin^{- 1} (k \sin (ϕ))

$\sin ^{-1}(k \sin (\phi ))$ :

And in order for the function to intersect a given point, you just need to make an equation and recalculate

k

$k$ :

\sqrt{\frac{2}{1 + \sqrt{1 - k^{'} \sin^{2} (\frac{π}{2})}}} = k

$\sqrt{\frac{2}{1+\sqrt{1-k' \sin ^2( \frac{\pi}{2} )}}}=k$

The code

Solve[(Sqrt[2/(1+Sqrt[1-k Sin[2 \[Phi]]^2])] /. \[Phi]->Pi/4)==x, k] /. x->k

↓

k^{'} \to \frac{4 (k^{2} - 1)}{k^{4}}

$k'\to \frac{4 \left(k^2-1\right)}{k^4}$

3) parameters

n

$n$ and

m

$m$ were just added in a creative way and their effects were investigated experimentally, in fact.

4) Rectangle is easy to get by going to the parametric view and "stretching" the axes

x = a \cos (t) \sqrt{\frac{2}{1 + \sqrt{1 - \sin^{2} (2 t)}}}

$x=a \cos (t) \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 t)}}}$

y = b \sin (t) \sqrt{\frac{2}{1 + \sqrt{1 - \sin^{2} (2 t)}}}

$y=b \sin (t) \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 t)}}}$

But after that

t

$t$ will no longer mean angle, now

t

$t$ Is just a parameter that describes a vector through its projections onto the coordinate axes. To go back to polar coordinates, you need to find the length of the vector (through the root of the sum of squares), the angle (through the arctangent of the ratio), express this angle through

ϕ

$\phi$ and substitute the resulting expression instead

t

$t$ ...

The code

With[{r = Sqrt[2/(1 + Sqrt[
      

        
        
        
      

    
 1 - Sin[2 t]^2])]}, {Sqrt[(a r Cos[t])^2 + (b r Sin[t])^2], 
      

        
        
        
      

    
 ArcTan[(b r Sin[t])/(a r Cos[t])]}] // Simplify

↓

{\sqrt{2} \sqrt{\frac{a^{2} \cos^{2} (t) + b^{2} \sin^{2} (t)}{\sqrt{\cos^{2} (2 t)} + 1}}, \tan^{- 1} (\frac{b \tan (t)}{a})}

$\left\{\sqrt{2} \sqrt{\frac{a^2 \cos ^2(t)+b^2 \sin ^2(t)}{\sqrt{\cos ^2(2 t)}+1}},\tan ^{-1}\left(\frac{b \tan (t)}{a}\right)\right\}$

Solve[ArcTan[(b Tan[t])/a]==\[Phi], t]

↓

t \to \tan^{- 1} (\frac{a \tan (ϕ)}{b})

$t\to \tan ^{-1}\left(\frac{a \tan (\phi )}{b}\right)$

Sqrt[2] Sqrt[(a^2 Cos[t]^2 + b^2 Sin[t]^2)/(1 + Sqrt[Cos[2 t]^2])]
      

        
        
        
      

    
/. t -> ArcTan[(a Tan[\[Phi]])/b] // Simplify

↓

\sqrt{2} \sqrt{\frac{a^{2} b^{2} \sec^{2} (ϕ)}{(a^{2} \tan^{2} (ϕ) + b^{2}) (\sqrt{\cos^{2} (2 \tan^{- 1} (\frac{a \tan (ϕ)}{b}))} + 1)}}

$\sqrt{2} \sqrt{\frac{a^2 b^2 \sec ^2(\phi )}{\left(a^2 \tan ^2(\phi )+b^2\right) \left(\sqrt{\cos ^2\left(2 \tan ^{-1}\left(\frac{a \tan (\phi )}{b}\right)\right)}+1\right)}}$

To simplify such a formula is already more difficult, and this will require several stages:

go to cartesian coordinates by replacing $\phi \to \tan ^{-1}(x,y)$ ;
go to exponential form;
simplify;
make a reverse replacement $x\to \cos (\phi )$ and $y\to \sin (\phi )$ ;
go back to exponential form;
simplify.

As a result, we get the following formula:

The code

Sqrt[2] Sqrt[(a^2 b^2 Sec[\[Phi]]^2) /
      

        
        
        
      

    
((1 + Sqrt[Cos[2 ArcTan[(a Tan[\[Phi]])/b]]^2])
      

        
        
        
      

    
(b^2 + a^2 Tan[\[Phi]]^2))] /. \[Phi] -> ArcTan[x, y] 
      

        
        
        
      

    
// TrigToExp // Simplify 
      

        
        
        
      

    
// # /. {x -> Cos[\[Phi]], y -> Sin[\[Phi]]} & 
      

        
        
        
      

    
// TrigToExp // Simplify // FullSimplify

↓

2 \sqrt{\frac{a^{2} b^{2}}{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2}) (1 + \sqrt{\frac{{((a^{2} + b^{2}) \cos (2 ϕ) - a^{2} + b^{2})}^{2}}{{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2})}^{2}}})}}

$2 \sqrt{\frac{a^2 b^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right) \left(1+\sqrt{\frac{\left(\left(a^2+b^2\right) \cos (2 \phi )-a^2+b^2\right)^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right)^2}}\right)}}$

Conclusion

As you can see, even in such a simple and banal thing as a polygon, you can find and come up with something new. And the story does not end there - the area formula for the general case remained unknown, the formula for an arbitrary, and not just regular, polygon remained unknown, and the expansion into power and trigonometric series was left without consideration. Also, probably, a similar kind of formula exists for the 3-dimensional case.

Therefore, if you are told that everything in mathematics has already been invented and there are only problems that are beyond the understanding of an ordinary person - do not believe it. There are many purely practical problems that real mathematicians are not aware of, or they are not interested in their solution due to the lack of sufficient hype around them, or because they already have a rough idea of ways to achieve them for their solution. Do not be afraid to tackle problems whose solutions are not available in Wikipedia, do not be afraid to publish their solutions, and do not be afraid to read the comments under the articles about the uselessness of everything.

PS download the original document for Mathematica here .

How to draw a star (and more) in polar coordinates

Complex form and modifications

Quads and stuff

Go to Cartesian coordinates

Appendix: how the formula was derived

Conclusion

More articles: