👨🏻‍✈️ 👩🏼‍🎤 🤳🏽 Where to solve analytical tasks from Yandex teams? Contest and analysis 😏 🖲️ 🧗

The trial round of the Yandex Cup programming championship begins today . This means that you can use the Yandex.Contest system to solve problems similar to those that will be in the qualifying round. So far, the result affects nothing.

In the post, you will find the terms of the tasks of the analytics track and analyzes, which are deliberately hidden in spoilers. You can see the solution or try to do the tasks yourself first. The check is automatic - the Contest will immediately report the result, and you will have the opportunity to propose another solution.

A. Count the liars in the country

^{Solve in Contest}

10,000 people live in the state. They are divided into lovers of truth and liars. Truth-lovers tell the truth with an 80% probability, and liars - with a 40% probability. The state decided to count the truth-lovers and liars based on a survey of 100 residents. Each time a randomly selected person is asked, "Are you a liar?" - and write down the answer. However, one person can take part in the survey several times. If a resident has already participated in the survey, he answers the same as the first time. We know that there are 70% of truth-lovers and 30% of liars. What is the probability that the state will underestimate the number of liars, that is, the survey will show that there are less than 30% of liars? Give your answer in percentage with a dot as a separator, round the result to the nearest hundredth (example of input: 00.00).

Decision

1. «» « ?».

«, » «» «» .

«, » :

: «» * = 0,2 * 0,7.

: «» * ( – ) + «» * ( ) = «» * = 0,2 * 0,7.

«, » 0,14 , . .

, «, » : 0,2 * 0,7 + 0,4 * 0,3 = 0,26.

2. .

, , — n = 100, p = 0,26.

, 30 (30% 100 ): P (x < 30). n = 100, p = 0,26 0,789458. : stattrek.com/online-calculator/binomial.aspx.

, : 78,95.

B. Theater season and telephones

^{Decide in Contest The}

international ticket service has decided to take stock of the theatrical season. As one of the metrics, the project manager wants to count the number of users who bought tickets for different performances.

When buying a ticket, the user indicates his phone number. You need to find the show with the largest number of unique phone numbers. And count the number of matching unique phone numbers.

Input format

Purchase logs are available in theticket_logs.csvfile. The first column contains the name of the performance from the service database. In the second - the phone number that the user left when purchasing. Note that for the sake of conspiracy, telephone country codes have been replaced with currently unserved zones.

Output format

The number of unique numbers.

Decision

main.py.

. . 801–807.

:

1. 8-(801)-111-11-11

2. 8-801-111-11-11

3. 8801-111-11-11

4. 8-8011111111

5. +88011111111

6. 8-801-flowers, — ( )

:

1. 1–4 replace.

2. 5 , 1. 11 , .

3. 6 , . , .

, . .

C. Calculate pFound

^{Solve in Contest}

Thearchivecontains three text files:

qid_query.tsv - the id of the query and the text of the query, separated by tabs;
qid_url_rating.tsv - request id, document URL, document relevance to the request;
hostid_url.tsv - host id and document url.

It is necessary to display the request text with the maximum value of the pFound metric, calculated from the top 10 documents. Issuance upon request is formed according to the following rules:

From one host there can be only one document on issue. If there are several documents for the request with the same host id, the most relevant document is taken (and if several documents are the most relevant, any one is taken).
Documents on demand are sorted in descending order of relevance.
If several documents from different hosts have the same relevance, their order can be arbitrary.

Formula for calculating pFound:

pFound =

\sum_{i = 1}^{10}

$\sum_{i=1}^{10}$ pLook [i] ⋅ pRel [i]

pLook [1] = 1

pLook [i] = pLook [i - 1] ⋅ (1 - pRel [i - 1]) ⋅ (1 - pBreak)

pBreak = 0.15

Output format

The request text with the maximum metric value. For example, for open_task.zip, the correct answer is:

Decision

. - — pFound . pandas — .

import pandas as pd

#  
qid_query = pd.read_csv("hidden_task/qid_query.tsv", sep="\t", names=["qid", "query"])
qid_url_rating = pd.read_csv("hidden_task/qid_url_rating.tsv", sep="\t", names=["qid", "url", "rating"])
hostid_url = pd.read_csv("hidden_task/hostid_url.tsv", sep="\t", names=["hostid", "url"])

#  join  ,     url   
qid_url_rating_hostid = pd.merge(qid_url_rating, hostid_url, on="url")

def plook(ind, rels):
 if ind == 0:
 return 1
    return plook(ind-1, rels)*(1-rels[ind-1])*(1-0.15)

def pfound(group):
 max_by_host = group.groupby("hostid")["rating"].max() #   
 top10 = max_by_host.sort_values(ascending=False)[:10] #  -10    
 pfound = 0
    for ind, val in enumerate(top10):
 pfound += val*plook(ind, top10.values)
 return pfound

qid_pfound = qid_url_rating_hostid.groupby('qid').apply(pfound) #   qid   pfound
qid_max = qid_pfound.idxmax() #  qid   pfound

qid_query[qid_query["qid"] == qid_max]

D. Sports tournament

^{Solve in Contest}

Time limit for the test	2 sec
Memory limit per test	256 MB
Input	standard input or input.txt
Output	standard output or output.txt

While Masha was on vacation, her colleagues organized a chess tournament according to the Olympic system. While resting, Masha did not pay much attention to this venture, so she can hardly remember who played with whom (there is no question of the order of the games). Suddenly Masha got the idea that it would be nice to bring a souvenir to the winner of the tournament from vacation. Masha does not know who won the final game, but she can easily figure out who played in it, if only she correctly remembered the playing pairs. Help her check if this is the case and identify potential winners.

Input format

The first line contains an integer 3 ≤ n ≤ 2 ¹⁶ - 1, n = 2 ^k - 1 - the number of past games. The next n lines contain two surnames of the players (in Latin capital letters) separated by a space. The names of the players are different. All surnames are unique, there are no namesakes among colleagues.

Input format

Print "NO SOLUTION" (without quotes) if Masha has memorized the games incorrectly and it is impossible to get a tournament according to the Olympic system using this grid. If the tournament grid is possible, print two surnames on one line - the names of the candidates for the first place (the order is not important).

Example 1

Input	Output
`7 GORBOVSKII ABALKIN SIKORSKI KAMMERER SIKORSKI GORBOVSKII BYKOV IURKOVSKII PRIVALOV BYKOV GORBOVSKII IURKOVSKII IURKOVSKII KIVRIN`	`IURKOVSKII GORBOVSKII`

Example 2

Input	Output
`3 IVANOV PETROV PETROV BOSHIROV BOSHIROV IVANOV`	`NO SOLUTION`

Notes The

Olympic system, also known as the playoffs, is a competition organization system in which a competitor is eliminated from a tournament after the first loss. You can read more about the Olympic system on Wikipedia .

Scheme of the first test from the condition:

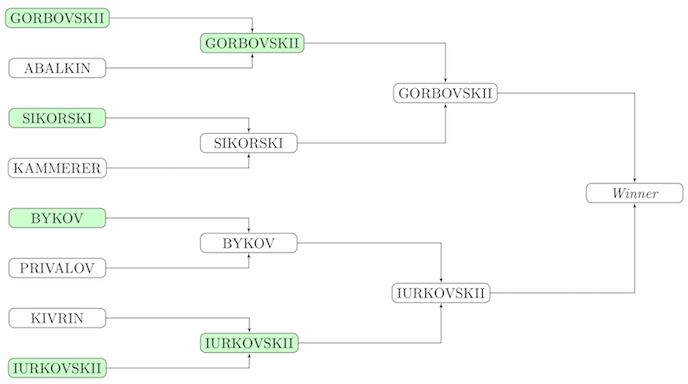
Decision

n = 2^k – 1 k. , i- , n_i. , ( k ). , . , i  j min(n_i, n_j), - ( ). r (i, j), min(n_i, n_j) = r. :

. 2^k – 1 , :

1. .

2. r 2^{k – r}.

. : , . k.  k = 1 — . k – 1 -> k.

-, , . , q . , q- . , 1, 2, ..., q. , , , , 2^k. , 2^{k – 1}   n_i = 1. .

, 2^{k – 1} n_i > 1 — . , n_i = 1 2^{k – 1}, . , : n_i = 1, — n_i > 1.   k – 1 ( n_i 1). , .

import sys
import collections

def solve(fname):
    games = []
    for it, line in enumerate(open(fname)):
        line = line.strip()
        if not line:
            continue
        if it == 0:
            n_games = int(line)
            n_rounds = n_games.bit_length()
        else:
            games.append(line.split())

    gamer2games_cnt = collections.Counter()
    rounds = [[] for _ in range(n_rounds + 1)]

    for game in games:
        gamer_1, gamer_2 = game
        gamer2games_cnt[gamer_1] += 1
        gamer2games_cnt[gamer_2] += 1

    ok = True
    for game in games:
        gamer_1, gamer_2 = game
        game_round = min(gamer2games_cnt[gamer_1], gamer2games_cnt[gamer_2])
        if game_round > n_rounds:
            ok = False
            break
        rounds[game_round].append(game)

    finalists = list((gamer for gamer, games_cnt in gamer2games_cnt.items() if games_cnt == n_rounds))

    for cur_round in range(1, n_rounds):
        if len(rounds[cur_round]) != pow(2, n_rounds - cur_round):
            ok = False
            break
        cur_round_gamers = set()
        for gamer_1, gamer_2 in rounds[cur_round]:

            if gamer_1 in cur_round_gamers or gamer_2 in cur_round_gamers:
                ok = False
                break
            cur_round_gamers.add(gamer_1)
            cur_round_gamers.add(gamer_2)

    print ' '.join(finalists) if ok else 'NO SOLUTION'

def main():
    solve('input.txt')

if name == '__main__':
    main()

To solve the problems of other tracks of the championship, you need to register here .

Where to solve analytical tasks from Yandex teams? Contest and analysis

A. Count the liars in the country

B. Theater season and telephones

C. Calculate pFound

D. Sports tournament

More articles: