🤞 🎹 🤹🏼 Geometric representation of the curvature of space in the Schwarzschild metric 🍟 🐅 👨🏻‍⚖️

... or two plus two equals four.

To understand the article, a school mathematics course is sufficient.

The form of the factor in the Schwarzschild metric has long haunted me with its exquisite duplicity, and I decided to devote some time to finding ways to transform it. The Schwarzschild metric itself is obtained as a result of solving general relativity for the vacuum case (the energy-momentum tensor is zero):

d s^{2} = - (1 - 2 \frac{G M}{c^{2} r}) c^{2} d t^{2} + {(1 - 2 \frac{G M}{c^{2} r})}^{- 1} d r^{2} + r^{2} \cdot d θ^{2} + r^{2} \cdot \sin^{2} θ \cdot d ϕ^{2}

It describes the space-time continuum in the vicinity of an arbitrary compact massive object. Compact, which means that the deviations of the form are insignificant in relation to the mass. To put it simply, round and tight. Usually a black hole is used here as an example. For some reason, no one gives examples of non-compact objects. An airtight foam stick in open space at an infinite distance from massive objects, such as a non-compact object. The cube horse in the distance, from which you can see the sadness in his eyes, too.

Through the volume of the 3-sphere

We will make a replacement:

M = \frac{E}{c^{2}}

Then the metric will become like this:

d s^{2} = - (1 - 2 \frac{G E}{c^{4} r}) c^{2} d t^{2} + {(1 - 2 \frac{G E}{c^{4} r})}^{- 1} d r^{2} + r^{2} \cdot d θ^{2} + r^{2} \cdot \sin^{2} θ \cdot d ϕ^{2}

The replacement was needed only to draw attention to the fourth degree of the speed of light, because all the numbers in the formulas are important. This is evidenced by the whole history of physics - any empirically obtained formula over time receives a theoretical basis, explaining the meanings of all mathematical forms that it contains.

Usually, in the representation of this metric, the part associated with physical constants and the mass of the body that creates the field is expressed in terms of the Schwarzschild radius:

r_{s} = 2 \cdot \frac{G E}{c^{4}}

because the metric has a singularity at this point. Here, time literally stops.

This is how the whole metric looks like:

d s^{2} = - (1 - \frac{r_{s}}{r}) c^{2} d t^{2} + {(1 - \frac{r_{s}}{r})}^{- 1} d r^{2} + r^{2} \cdot d θ^{2} + r^{2} \cdot \sin^{2} θ \cdot d ϕ^{2}

But in continuation of reasoning about the physical essence of phenomena, this two:

r_{s} = 2 \cdot \frac{G E}{c^{4}}

must also be comprehended. Therefore, we represent it like this:

u = \frac{G E}{c^{4}}

It's just half the gravitational radius

r_{s}

, and its dimension is the same. We get:

1 - 2 \frac{G E}{c^{4} r} = 1 - 2 \frac{u}{r}

It suggests itself:

= (1 - 2 \frac{u}{r} + \frac{u^{2}}{r^{2}}) - \frac{u^{2}}{r^{2}} = {(1 - \frac{u}{r})}^{2} - \frac{u^{2}}{r^{2}} = {(\frac{r - u}{r})}^{2} - \frac{u^{2}}{r^{2}} =

= \frac{(r - u)^{2} - u^{2}}{r^{2}} (1)

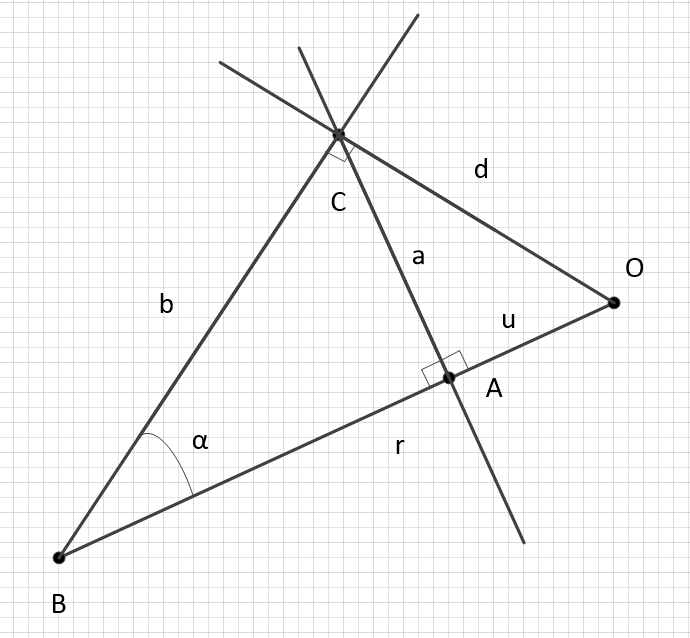
Not bad already. Let's draw. Imagine

r = O B

end segment,

u = O A

- part of it, as shown in the figure below. It's obvious that

(r - u) = A B

...

It is curious, by the way, which of

r_{s} = 2 u

it follows that the point

A

is located behind (under) the event horizon of the energy object

E

... It's so easy to find it, but we can't.

Now we will show that a relation of the form

(1)

will be carried out for all points that have a geometric place on the perpendicular to

O B

at the point

A

\frac{(r - u)^{2} - u^{2}}{r^{2}} = \frac{((r - u)^{2} + a^{2}) - (u^{2} + a^{2})}{r^{2}} = \frac{b^{2} - d^{2}}{r^{2}} (2)

for any

b = C B

and

d = O C

...

Simply put, the difference of squares

(r - u)^{2} - u^{2}

is equivalent to the difference of any quantities whose projections onto

O B

are

A B

and

O A

respectively, provided that the point

C

they have in common.

Further, suppose that

u = u (E)

and

(r - u)

conversely, projections

r = O B

on some axes, that is, the Pythagorean sum of two quantities, in their original form, perpendicular to each other. Translating this into a requirement, consider the case

∠ O C B = π / 2

for which it is true:

b^{2} = r^{2} - d^{2} \to (2) \to \frac{b^{2} - d^{2}}{r^{2}} = 1 - 2 \frac{d^{2}}{r^{2}} (3)

We will finalize

(3)

similar to the initial iteration:

1 - 2 \frac{d^{2}}{r^{2}} = (1 - 2 \frac{d^{2}}{r^{2}} + \frac{d^{4}}{r^{4}}) - \frac{d^{4}}{r^{4}} = \frac{(r^{2} - d^{2})^{2} - d^{4}}{r^{4}} =

= \frac{b^{4} - d^{4}}{{\sqrt{b^{2} + d^{2}}}^{4}} = \frac{b^{4} - d^{4}}{r^{4}} (4)

Here is the fourth degree. Formula for the volume of a 3-sphere:

V = \frac{π^{2} \cdot R^{4}}{2}

This I mean that if you multiply and divide

(4)

π^{2} / 2

\frac{b^{4} - d^{4}}{r^{4}} = \frac{π^{2}}{2} \cdot \frac{2}{π^{2}} \cdot \frac{b^{4} - d^{4}}{r^{4}} = \frac{V_{b} - V_{d}}{V_{r}} (5)

then the factor in the Schwarzschild metric turns into the difference between the volumes of two 3-spheres built around two radial projections of a point relative to the center of the field, correlated to the volume of a 3-sphere formed by the total distance between the point and the center of the field.

Taking into account the fact that the total radius is given by projections, this whole construction is very succinctly set by two parameters, one of which is related to energy, and the second is not. There are exactly two coordinates.

conclusions

The remarkable consequences of such a representation are:

1. From the form of the multiplier it is seen that the behavior of the photon limits the visible zone of the five-dimensional space-time. Outside of it, you can hide something gravitating, but invisible.

2. The presence of the second hidden coordinate eliminates the zero time paradox.

3. Since the curvature of space around a massive body can always be decomposed into two components, one of which is associated with the energy of the body, and the second exclusively with space, then the next step is to solve the equations of general relativity for the vacuum case of five-dimensional space-time. More on this in the next article.

Bonus. Across the corner

Obviously, it is possible to express the significance of the field at a point through a flat angle, which expresses the deviation of the trajectory of motion from flat space (in the absence of gravitational fields).

Let us express the quantities

b

and

d

across the corner

α = ∠ O B C

b = r \cdot \cos α; d = r \cdot \sin α

... Let's call it the angle of curvature of the trajectory. Then the factor can be expressed in very different ways:

1 - 2 \frac{G E}{c^{4} r} = \cos^{2} α - \sin^{2} α = \cos^{4} α - \sin^{4} α = 1 - 2 \sin^{2} α =

= \frac{1 - \tan^{2} α}{1 + \tan^{2} α} = \cos 2 α (6)

I especially like the tangent version.

Substitute in the original interval:

d s^{2} = - \cos 2 α \cdot c^{2} d t^{2} + \cos^{- 1} 2 α \cdot d r^{2} + r^{2} \cdot d θ^{2} + r^{2} \cdot \sin^{2} θ \cdot d ϕ^{2}

Everything, as it should, turns into a flat Minkowski metric for

α = 0

...

There should definitely be a fifth ...

To be continued.

Geometric representation of the curvature of space in the Schwarzschild metric

Through the volume of the 3-sphere

conclusions

Bonus. Across the corner

More articles: