🏈 👲🏿 👨🏻‍💼 Review of the cryptographic protocol of the remote electronic voting system 🐼 ✈️ 💇🏿

In this article, we will analyze the details of the implementation of the cryptographic protocol of the remote electronic voting system.

The use of cryptographic mechanisms and algorithms at various stages of the electoral process gives the remote voting system the necessary properties. Let's take a closer look and consider the stages of voting described in the overview article .

System initialization. At the stage of voting initialization, the following cryptographic operations are performed:

Development of a validator key pair for issuing and verifying a blind signature, as the most persistent and recommended by the academic community for anonymization procedure in electronic voting systems. At the moment, the system supports blind signature algorithms on elliptic curves and based on the RSA encryption algorithm. The voting was carried out using an algorithm for issuing and verifying a blind signature based on the RSA encryption algorithm with a key length of 4096 bits.
Generation of a shared public encryption key. For greater security in the key generation process, two cryptographic algorithms are used at once: the DKG Pedersen 91 distributed key generation protocol and the Shamir key sharing protocol. Key generation is carried out both by participants who have the technical means to control directly the network nodes and the counting server, and by participants who are the keepers of the keys recorded on external media. The result of the work of these two algorithms is a common public key for encrypting ballots. Below we will take a closer look at the procedure for generating this key.

Providing access to the newsletter . At this stage, the following mechanisms work:

Generation of a key pair of an electronic signature on a voter's device in accordance with GOST R 34.10-2012
Generation of a blind signature for the voter's masked public key for certification and subsequent verification of his right to take part in the vote. The mechanism is currently based on the RSA encryption algorithm. The anonymization mechanism is discussed in detail in a separate article.

Filling out and sending the newsletter . At this stage, the following set of cryptographic algorithms is used:

Elliptic curve encryption of the newsletter according to the ElGamal scheme. This scheme is used in the protocol, since it has the property of being homomorphic in addition, which makes it possible to obtain voting results without decrypting each ballot.
Disjunctive Chaum-Pedersen range proof is used to prove the correctness of the content of the ballot without decrypting it. We will analyze this mechanism in detail in the next article.
Electronic signature of the encrypted bulletin in accordance with GOST R 34.10-2012.

Counting the totals. At the stage of summing up, the following is performed:

Homomorphic addition of encrypted ballots.
Preliminary partial decryption of the final summarized ballot by parts of the private key by the participants controlling individual nodes and counting servers with the receipt of ciphertexts from each participant;
Assembling the private key in the Election Commission and partial decryption of the final summarized ballot with the collected key.
The final summation of the ciphertexts and the receipt of the counting results.
Generation and verification of a Chaum-Pedersen zero knowledge proof. Used to prove the correctness of decryption of the final summarized ballot. We will analyze this mechanism in detail in the next article.

Audit . At this stage, validation checks of all stages of the protocol can be performed, and in this article we will take a closer look at possible checks.

Let's take a closer look at the cryptographic mechanisms.

Blockchain platform

Before talking about the procedure for generating keys, you need to give an introduction to the implementation of the blockchain platform.

The figure below shows a simplified target layout of the blockchain platform.

The placement and reservation of blockchain nodes takes place in geographically distributed data centers of PJSC Rostelecom. In this case, the responsibility for the "atomic" set of components involved in storing all voting data can be assigned to the election commission or various institutions of public observation.

This is done in order to provide participants with the opportunity to control the main components of the system and network nodes, and at the same time not deal with issues with information security, deployment and operation of technical means, as well as ensuring the scalability of the system.

The list of participants can change over time - from a minimal one at the stage of launching the system into commercial operation, to a fairly wide and completely decentralized one as the system develops. Moreover, there is always the possibility of placing a set of components outside the data center.

The domestic solution Waves Enterprise is used as a blockchain platform. Transactions and blocks are signed in accordance with GOST R 34.10-2012.

Generating encryption keys

The public key for ballot encryption is generated using two cryptographic algorithms: the DKG Pedersen 91 Distributed Key Generation Protocol and the Shamir Key Sharing Protocol. On the basis of each of these algorithms, an “intermediate” public key is generated. Then these two keys are combined into one common one.

The key assembly diagram is shown below in the figure.

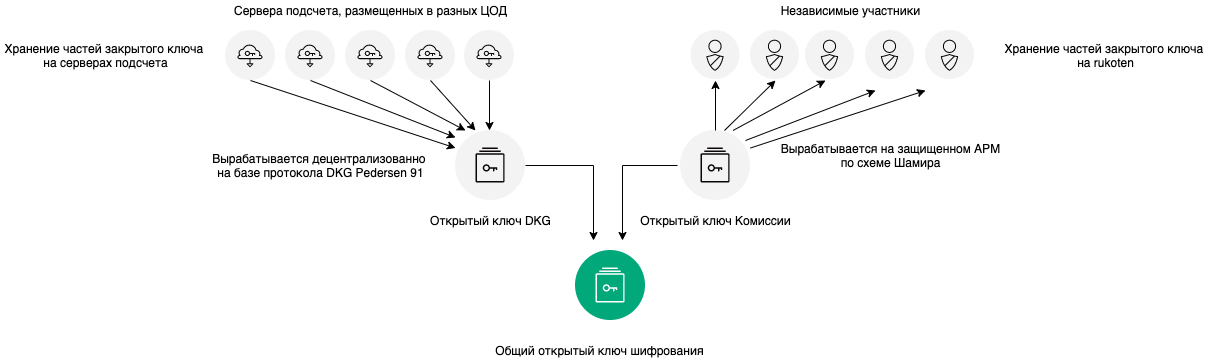
In general, such a scheme may seem redundant, but this is how we can get maximum confidentiality of the vote before it ends. This is due to the fact that the private key generated using the DKG protocol is never in one place in the assembled form and cannot be maliciously stolen before or after generation, and its parts are owned by independent parties that interact with each other only through the blockchain.

But if you can not assemble a quorum independent participants blokcheyn-network routine starts separating key between independent parties, who are the guardians of the individual parts of the key to be recorded to external media (the Commission's key)

procedure for a common public key encryption begins on the eve of the vote, making procedure open to the Commission the key... At a certain point in time before the start of voting, in the presence of observers and journalists on a secure laptop not connected to a local network or the Internet, using a special utility, a key pair is generated, followed by dividing the private key into n1 parts and recording them on special media. The election commission, by its decision, determines the carriers of the parts of the private key. At the stage of creating and initializing a vote, the public key of the commission will be recorded in the blockchain.

Then the creation of voting in the blockchain network is initiated. After creating a vote on the counting servers, the procedure for generating the DKG public key is automatically started .

Participants in the distributed key generation procedure are n vote counting servers, which we wrote about earlier in the review article . All operations of interaction between counting servers, both intermediate and final, are recorded in the blockchain, and, therefore, are transparent and verifiable. The system implements the "k out of n" threshold scheme, that is, when decrypting the data, the participation of all n parties that formed the public key DKG is not required, a smaller number of participants k is sufficient. This allows decryption of voting results even if nk counting servers are unavailable or their private keys have been lost.

To generate a public key, the DKG (Distributed Key Generation) algorithm is used, described in the article "A threshold cryptosystem without a trusted party" by Torben Pryds Pedersen, transferred to elliptic curves. It is assumed that each server has a constant (recorded by the registrar in the accountant) Diffie-Hellman key pair used for secure data transmission to this server (export / import of key shares).

Protocol parameters

An elliptic curve E and a generator P of a subgroup of this curve of large prime order q. The current implementation uses the secp256k1 curve .
Another generator Q of the same subgroup for which the value $x: Q=x⋅P$ unknown to anyone.
(k, n), where n is the total number of participants who generated key pairs, and k is the minimum number of participants that is necessary to restore the shared secret, while $k≤(n+1)/2$ ... That is, if k-1 participants are compromised or their keys are stolen, this will not affect the security of the shared secret in any way.

In general, the algorithm for obtaining point Q is as follows: any sequence of bytes is taken, for example the string “Hello, World!”, And the hash h = Hash (“Hello, World!”) Is calculated from it, after which we convert the sequence of bytes h to a number and consider

x 0 = h m o d p

$x0=h mod p$ , where p is the modulus of the curve, we substitute

x 0

$x0$ into the curve equation:

y^{2} = x 0^{3} + a * x 0 + b m o d p

$y^2= x0^3+ a*x0+b mod p$ and trying to solve it with respect to y. In the absence of a solution, we increment x0 and again try to solve the equation for a new value of x0, and so on.

Step 0.

Each of the n servers is assigned a unique sequence number from 1 to n. This is necessary because the Lagrange coefficient depends on the server serial number.

Step 1 - creating a public key DKG.

Each j -th server, j = 1, ..., n:

1. Generates a pair of private key 〖priv〗 _j and a public key

P u b_{j} = p r i v_{j} \cdot P .

$Pub_j=priv_j⋅P.$

2. Makes a Pedersen commitment for the public key:

Generates a random number r_j

Calculates a point

C_{j} = r_{j} \cdot Q + P u b_{j}

$C_j=r_j⋅Q+Pub_j$

C_{j}

$C_j$ is published using meter

3. After all servers have published their C_i values, the scalar r_j is published.

Using scalars, anyone can recover the public keys of each server

P u b_{j} = C_{j} - r_{j} \cdot Q

$Pub_j=C_j-r_j⋅Q$ and calculate the public key DKG

P u b = \sum_{(} j = 1)^{n} P u b_{j}

$Pub=∑_(j=1)^n Pub_j$ ...

The public key DKG is written to the blockchain.

Step 2 - generating polynomials and distributing shadows.

Each j -th server, j = 1,…, n:

1. Generates a randomly polynomial of degree k-1:

f_{j} (x) = f_{(} j, 0) + f_{(} j, 1) \cdot x + \dots + f_{(} j, k - 1) \cdot x^{(} k - 1),

$f_j (x)=f_(j,0)+f_(j,1)⋅x+⋯+f_(j,k-1)⋅x^(k-1),$

where the coefficient

f_{(} j, 0) = p r i v_{j}

$f_(j,0)=priv_j$ , and the rest are random elements of the field GF (q).

2. Counts the values of the polynomial

f_{j} (i), i = 1, \dots, n, i \neq j .

$f_j (i),i=1,…,n,i≠j.$

3. Encrypts the value

f_{j} (i)

$f_j (i)$ using the public export / import key, the i -th server for each i and publishes the encryption results using the meter.

Step 3 - checking the coefficients of the polynomials.

Each j -th server, j = 1, ..., n:

1. Publishes each coefficient of its polynomial multiplied by the generator P.

F_{(} j, 0) = f_{(} j, 0) \cdot P, F_{(} j, 1) = f_{(} j, 1) \cdot P, \dots, F_{(} j, k - 1) = f_{(} j, k - 1) \cdot P

$F_(j,0)=f_(j,0)⋅P,F_(j,1)=f_(j,1)⋅P,…,F_(j,k-1)=f_(j,k-1)⋅P$

2. Decodes all meanings

f_{i} (j), i = 1, . ., n, i \neq j

$f_i (j),i=1,..,n,i≠j$ and checks their correctness:

Calculates

A = f_{i} (j) \cdot P

$A=f_i (j)⋅P$

Calculates the sum

If A = B, then the result is accepted, otherwise a complaint is published against server i, and the protocol is started from the very beginning - go to step 0.

3. If no one has complaints, then it calculates its private key. The

public key DKG can be recovered and verified against the data that the counting servers write to the blockchain at the stage of voting initiation. It is necessary to take the public key points of all decrypts and add them. The result will be the same value that is recorded in the blockchain as the public key DKG.

Further, based on the public key of the commission, which is loaded into the system, and the public keys of the counting servers, a common public encryption key is generated according to the following formula:

MainPubKey = Hash (PubDKG, PubCommission) * PubDKG + Hash (PubCommission, PubDKG) * PubCommission

All public keys are written to the blockchain along with intermediate computations for easy inspection by observers. The shared public encryption key is read from the blockchain and transmitted to users' devices when the newsletter is displayed.

Description of the Bulletin Encryption Scheme

Below is a description of the procedure for encrypting ballots using the El-Gamal scheme on elliptic curves.

The El Gamal encryption scheme on elliptic curves allows one to implement encryption that is homomorphic with respect to addition, in which, as a result of the addition operation over the cipher text, an encrypted sum of the original values is obtained.

Encrypted (A) + Encrypted (B) = Encrypted (A + B).

To use this property of the algorithm, the completed electronic ballot is represented as a string of zeros and ones. The number of characters corresponds to the number of choices, while the selected one is represented by one, the other choices are represented by zeros.

The length of the private key when using the ElGamal algorithm on elliptic curves is selected to be 256 bits, while the public key is a point on the elliptic curve. This corresponds to a security level of 128 bits (2 ^ 128 curve point operations are required to crack). This level is considered optimal for most modern industrial and financial systems, including the Russian standard GOST 34.10-2018 “Information technology. Cryptographic information protection. Processes of Formation and Verification of Electronic Digital Signatures "(256 bit version)

Secp256k1 is used as the elliptic curve.

Let's say we have a key pair priv, Pub:

Number priv: 0 <priv <q

Point Pub = priv * Base

Encryption:

There is a message m, a small number that we want to encrypt on the Pub key.
Calculate the point M = m * Base
Generate a random number r: 0 <r <q
Calculate point R = r * Base and point C = M + r * Pub
Ciphertext: (R, C)

Decryption:

There is a private key priv and ciphertext (R, C)
Calculate point M = C - priv * Base
Reconstructing m: solving by brute-force ECDLP for the ratio M = m * Base

Scheme homomorphism.

We see that if we encrypt two messages

M 1 = m 1 * B a s e

$M1 = m1*Base$ and

M 2 = m 2 * B a s e

$M2 = m2*Base$ on the Pub key:

(R 1, C 1) = (r 1 * B a s e, M 1 + r 1 * P u b)

$(R1, C1) = (r1*Base, M1 + r1*Pub)$

(R 2, C 2) = (r 2 * B a s e, M 2 + r 2 * P u b)

$(R2, C2) = (r2*Base, M2 + r2*Pub)$

Then their sum

(R 1 + R 2, C 1 + C 2)

$(R1 + R2, C1 + C2)$ matches the encrypted message

M 1 + M 2

$M1 + M2$ ...

Thus, all ballots can be encrypted and folded "candidate-by-candidate". For example, let an open bulletin look like this:

Ivanov Petrov Sidorov

0 1 0

Then, transforming it into points, we get:

Ivanov Petrov Sidorov

ZeroPoint Base ZeroPoint

where ZeroPoint is a point at infinity.

And finally, we encrypt the newsletter on the Pub key:

Ivanov Petrov Sidorov

(r 1 * B a s e, r 1 * P u b)

$(r1*Base, r1*Pub)$

(r 2 * B a s e, B a s e + r 2 * P u b)

$(r2*Base, Base + r2*Pub)$

(r 3 * B a s e, r 3 * P u b)

$(r3*Base, r3*Pub)$

Let's say that we have conducted such a vote with N voters. If for Ivanov, Petrov and Sidorov we add separately the ciphertexts from different ballots, then we get a summary ballot, which contains encrypted amounts for each of the candidates. This summary ballot can be decrypted with the decryption key and the results of voting for each of the candidates can be found.

The figure below shows a scheme of homomorphic ballot stacking and validation based on zero knowledge proofs.

As we can see from the diagram, a potential attacker has no way to "throw in" extra votes by encrypting an incorrect number at the level of the cryptographic protocol. This is accomplished using zero knowledge proofs, which will be discussed later in the article. In addition, the necessary checks are also implemented in the voter's web application.

Description of the decryption procedure

The votes are counted without decryption due to homomorphic encryption according to the El-Gamal scheme, which allows maintaining the confidentiality of the entire voting procedure and each individual vote. Also, none of the servers has the ability to independently and secretly decrypt the voting results.

In order to decrypt the ciphertext (R, C), it is necessary that any k out of n servers compute and publish the value

s_{j} \cdot R

$s_j⋅R$ and proof of the correctness of the Chaum-Pedersen decryption (proof that the calculated

s_{j} \cdot R

$s_j⋅R$ Is precisely the point R multiplied by

s_{j}

$s_j$ without revealing the meaning

s_{j}

$s_j$ ). Also, for this, it is necessary to collect the private key of the commission from at least k1 from t1 parts and with its help also perform the calculation

s_{j} \cdot R

$s_j⋅R$ with publication to the blockchain.

Decryption occurs in several stages, the results of each of which are recorded in the blockchain.

First step- partial decryption. Each K of the N servers of the system adds the ciphertexts of the votes, receives the summary ballot, and decrypts the private voting key on its part. The result of this operation will be a ciphertext, the combination of which with the ciphertexts obtained as a result of the same operations performed on the other counting servers, as well as with the ciphertext received on the closed commission key, will give a decrypted final result. It is important to note that if there is no ciphertext obtained from decryption on the private key of the commission, all other ciphertexts become useless. It is impossible to get any results from them.

The results of the operation are published on the blockchain.

Second phase- assembly of the private key of the commission and partial decryption of the summary ballot. This operation is performed on a special PC without an Internet connection. After the key is collected, the operation described in the previous paragraph takes place to form the ciphertext on the commission key. The results of this operation are also recorded on the blockchain.

The third stage is the final decoding. The voting counting servers aggregate the results K from N servers, the decryption result on the commission's private key, and produce the final decryption, then publish the voting results.

Please note that the presence of the ciphertext generated on the private key of the commission is a prerequisite. Without it, the calculation of the results will not take place.

Based on the published results of the partial decryption, any interested party can repeat the process and verify that the results are counted correctly.

Zero knowledge proof

Although the DEG system is protected from intruders and user errors at the software and infrastructure level, additional mathematical proofs and checks were provided at the level of the cryptographic protocol, which do not allow transferring false information to the system. For this, several mechanisms have been developed based on non-interactive zero-knowledge proof (NIZK).

The first type of ZKP (zero-knowledge proof) applied in the system is range proofs. The ZKP data is used when publishing an encrypted ballot so that, in the absence of information about how the voter voted, it would be possible to make sure that the voter did not spoil the ballot on his device in one of the following ways:

the participant did not encrypt a value greater than one in the ballot for a separate voting option, which would affect the voting result in case of "encrypted addition";
the participant did not choose more than one option for each question in the ballot, unless it is provided for by the procedure for filling out the ballot.

A more detailed description of the NIZK implementation, as well as their verification, will be discussed in a separate article.

Structure of records in the blockchain

All information in the blockchain is recorded by three types of transactions:

CreateContract - to create a smart contract for a specific vote. Further in this smart contract all information on voting will be aggregated. If two (or more) votes are held simultaneously, then two (or more) copies of the contract are created, respectively.
CallContract - for interacting with a smart contract for various operations, a list of which is given below.
Data transaction - for recording a voter list after creating an instance of a voting smart contract and before starting the voting itself.

Interaction with a smart contract is performed by the following operations:

Writing basic data to a smart contract. The public keys of the counting servers that will participate in the cryptographic protocol, the threshold scheme, blind signature verification keys and other data necessary for organizing the protocol and voting in general are stored here.
dkgScalar, dkgCommit, dkgShadows - data required to build a public key for encryption of ballots and implement a threshold k of n schemes. We'll talk more about this later in the article.
addMainKey – .
blindSigIssue – .
vote – .
finishVoting – . .
Decryption – . .
ComissionDecryption – .
Results – . , .

A voter vote transaction includes a voter's blockchain address and public key, an encrypted ballot, a blind signature, and an electronic signature generated on the voter's anonymous private key (see previously published article on anonymization).

The figures below show the display of a transaction with a voice in the blockchain client.

All information about voting is aggregated on a smart contract and will be available through the blockchain client to observers or in the form of a csv file to anyone who wishes.

The figure below shows the display of aggregated information in a smart contract.

* Data from the test server.

Features of the Waves Enterprise platform allow you to implement a rather complex logic with a status model, blind signature verification, and counting valid and spoiled ballots.

Cryptographic protocol and voting process checks

The first basic check that can be done using the blockchain platform and the blockchain client is to check whether the number of voters on the voter list matches the number of ballots issued and the number of votes recorded.

Checking the correctness of counting is carried out by repeating the work of the counting server by the observer to summarize encrypted ballots candidate by candidate. This is done by sequentially adding the points of the elliptic curve corresponding to each candidate.

Then, using the received encrypted summary bulletin and the decryption proof, which are published on the blockchain, the correctness of the summation and partial decryption performed by each counting server can be verified.

At this stage, you can see whether the encrypted amount received by the observer corresponds to what each of the counting servers recorded.

After that, you can check the correctness of decryption of the voting results. To do this, you need to take ciphertexts from transactions with the type of operations Decryption and CommissionDecryption and, by analogy with ballots, add the points of the elliptic curve for each candidate.

The source code for the cryptographic operations is available in this GitHub repository.

Review of the cryptographic protocol of the remote electronic voting system