✌🏽 🎆 😹 Machine Learning. Neural Networks (Part 3) - Convolutional Network under the microscope. Exploring the Tensorflow.js API 👩🏿‍🎓 🍊 👶🏻

See also:

In previous articles, only one of the types of neural network layers was used - dense, fully-connected, when each neuron of the original layer has a connection with all neurons from the previous layers.

To handle, for example, a 24x24 black and white image, we would have to turn the matrix representation of the image into a vector that contains 24x24 = 576 elements. As you can imagine, with such a transformation we lose an important attribute - the relative position of pixels in the vertical and horizontal directions of the axes, and also, probably, in most cases, the pixel located in the upper left corner of the image hardly has any logically explainable effect on the pixel in lower right corner.

To eliminate these shortcomings, convolutional layers (CNN) are used for image processing.

The main purpose of CNN is to extract small parts from the original image that contain supporting (characteristic) features (features), such as edges, contours, arcs or faces. At the next processing levels, more complex repeatable fragments of textures (circles, square shapes, etc.) can be recognized from these edges, which can then be folded into even more complex textures (part of the face, car wheel, etc.).

For example, consider a classic problem - image recognition of numbers. Each number has its own set of figures characteristic of them (circles, lines). At the same time, each circle or line can be composed of smaller edges (Figure 1)

Figure 1 - The principle of operation of sequentially connected convolutional layers, with the allocation of characteristic features at each of the levels. Each of the next layers from a set of daisy-chained CNN layers extracts more complex patterns based on the previously identified ones. — 1 – , . CNN , .

1. (convolutional layer)

CNN ( ), c () , . – CNN – .

, 2x2 ( K) , 2x2 ( N), :

$\left[\begin{matrix}n_{11}&n_{12}\\n_{21}&n_{22}\\\end{matrix}\right]\ast\left[\begin{matrix}k_{11}&k_{12}\\k_{21}&k_{22}\\\end{matrix}\right]=n_{11}k_{11}+n_{12}k_{12}+n_{21}k_{21}+n_{22}k_{22}$

, .

, (fully-connected, dense layers):

${sum=\ \vec{X}}^T\vec{W}=\sum_{i=1}^{n=4}{x_iw_i}=x_1w_1+x_2w_2+x_3w_3+x_4w_4$

, - , – - , ( ).

2. , , , .

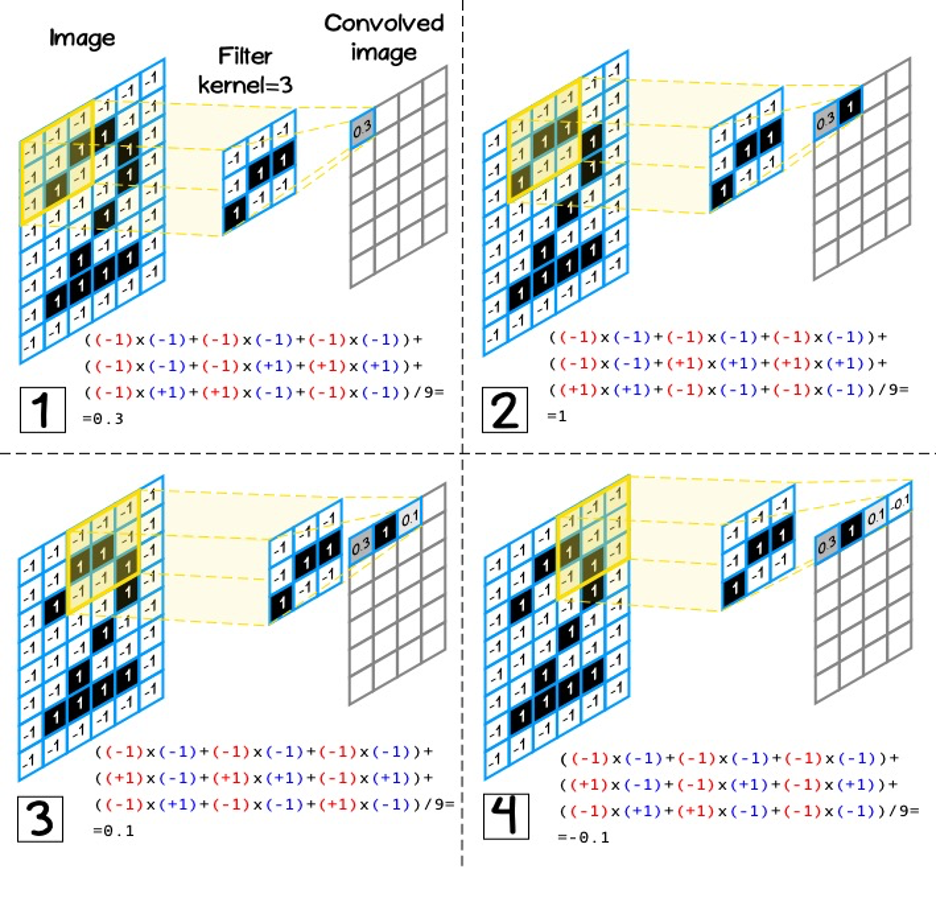
(kernel size) – 3, 5, 7.

(kernel) [k_h, k_w], [n_h, n_w], ( 3):

, . , . , .

, – (padding). , . , p_h p_w , :

, , , :

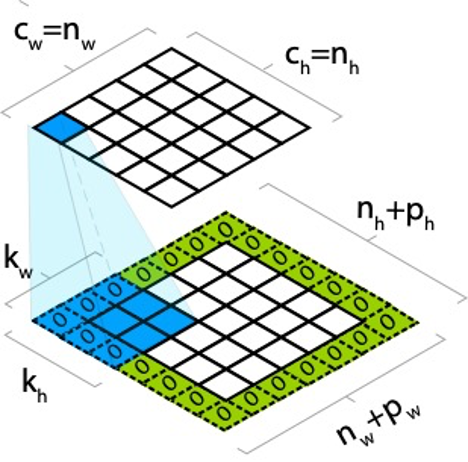
- . , (stride). – (stride).

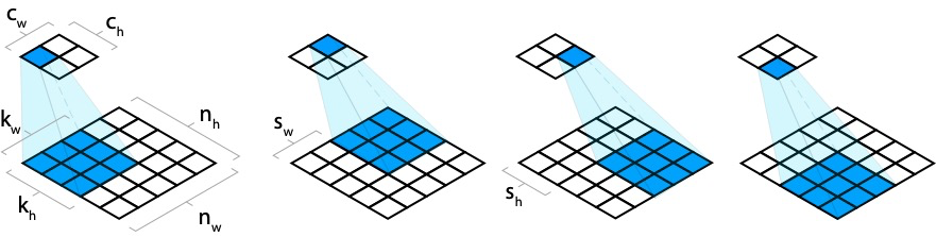
, s_w, s_h, :

$c_w=\left \lfloor (n_w+p_w-k_w+s_w)/s_w \right \rfloor; c_h=\left \lfloor (n_h+p_h-k_h+s_h)/s_h \right \rfloor$

, ( – ). (). , (CONV1) 9x9x1 ( – - ), 2 1x1 (stride) (padding) , , . 9x9x2 2 – (. 6). CONV2 , , 2x2, , 2, 2x2x2. (CONV2) 9x9x4, 4 – .

Figure 6 - Changing the dimension of tensors after several consecutive convolutional layers — 6 –

, k_w k_h , n_wx n_hx n_d, n_d - , , k_w x k_h x n_d ( 6, CONV2).

7 , RGB, 3x3. , (3 ), 3x3x3.

Figure 7 - Calculations in the convolutional layer if the input image has three RGB channels — 7 - , RGB

TensorFlow.js

, : tf.layers.conv2d, – , :

- filter – number –

- kernelSize – number | number[] – , number, , –

- strides – number | number[] - , [1,1], .

- padding – ‘same’, ‘valid’ – , ‘valid’

'same'

, , () (stride) . , - 11 , – 5, 13/5=2.6, – 3 ( 8).

stride=1, ( 9), , ( 8).

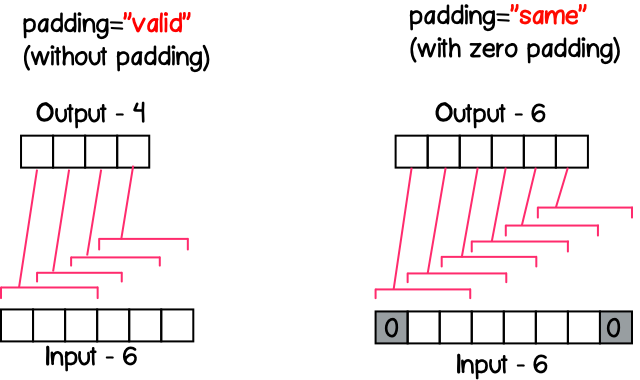
'valid'

, strides , 8.

TensorFlow.js

, . :

- :

$\ left [\ begin {matrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\\ end {matrix} \ right]$

- :

$\ left [\ begin {matrix} 1 & 1 & 1 \\ 0 & 0 & 0 \\ - 1 & -1 & -1 \\\ end {matrix} \ right]$

, , tf.browser.fromPixels. , img canvas .

<img src="./sources/itechart.png" alt="Init image" id="target-image"/>
<canvas id="output-image-01"></canvas>

<script>
   const imgSource = document.getElementById('target-image');
   const image = tf.browser.fromPixels(imgSource, 1);
</script>

, , , 3x3, “same” ‘relu’:

const model = tf.sequential({
    layers: [
        tf.layers.conv2d({
            inputShape: image.shape,
            filters: 1,
            kernelSize: 3,
            padding: 'same',
            activation: 'relu'
        })
    ]
});

[NUM_SAMPLES, WIDTH, HEIGHT,CHANNEL], tf.browser.fromPixel [WIDTH, HEIGHT, CHANNEL], – ( , ):

const input = image.reshape([1].concat(image.shape));

. , setWeights Layer, :

model.getLayer(null, 0).setWeights([
    tf.tensor([
         1,  1,  1,
         0,  0,  0,
        -1, -1, -1
    ], [3, 3, 1, 1]),
    tf.tensor([0])
]);

, , 0-255, NUM_SAMPLES:

const output = model.predict(input);

const max = output.max().arraySync();
const min = output.min().arraySync();

const outputImage = output.reshape(image.shape)
    .sub(min)
    .div(max - min)
    .mul(255)
    .cast('int32');

canvas, tf.browser.toPixels:

tf.browser.toPixels(outputImage, document.getElementById('output-image-01'));

2. (pooling layer)

, ( ), , . , , (pooling layer, subsample layer), . MaxPooling .

, .

. (kernel) , (stride) 1x1, . , (. 10).

Figure 10 - Transformation in the subsample layer — 10 –

, 4x4, 2x2 (stride) , 2x2, .

, ( 11) . , , MaxPooling . (translation invariance). , , 50%. , , MaxPooling .

Figure 11 - Smoothing spatial displacements after MaxPooling layer — 11 – MaxPooling

, .

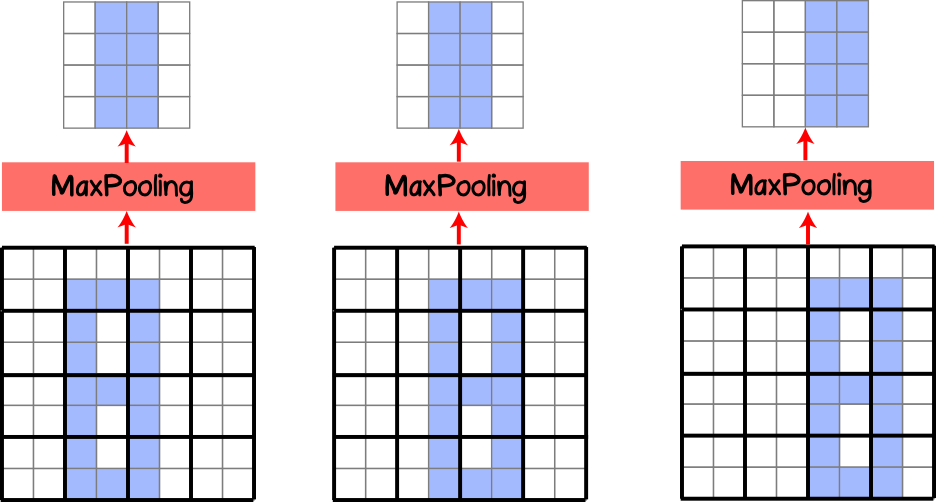
, , – (stride).

MaxPooling AveragePooling, , , . , MaxPooling. AveragePooling , , MaxPooling .

TensorFlow.js (pooling layer)

tf.layers.maxPooling2d tf.layers.averagePooling2d. – , :

- poolSize - number | number [] - the dimension of the filter, if number is specified, then the dimension of the filter takes a square form, if it is specified as an array, then the height and width may differ

- strides - number | number [] is a promotion step, an optional parameter and by default has the same dimension as the specified poolSize.

- padding - 'same', 'valid' - setting zero padding, by default 'valid'

Machine Learning. Neural Networks (Part 3) - Convolutional Network under the microscope. Exploring the Tensorflow.js API

1. (convolutional layer)

TensorFlow.js

'same'

'valid'

TensorFlow.js

2. (pooling layer)

TensorFlow.js (pooling layer)

More articles: