🍹 💂 🎂 Simple and rigorous proof of 26/10 dimensions in string theory 🐒 💀 🚟

... you won't find it anywhere.

, . - (26 10 ) , , , . , .

, D- -, D−2 , , ( , ). , 1D- - 2D-, . — , . D-2.

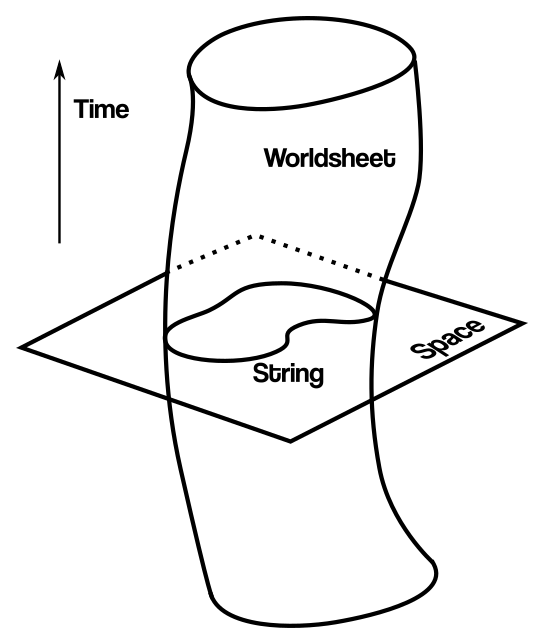
24- . , 24 — . , :

1^{2} + 2^{2} + 3^{2} + \dots + 23^{2} + 24^{2} = 70^{2}

$1^2 + 2^2 + 3^2 + \ldots + 23^2 + 24^2 = 70^2$

24, 0 1, . ( , . ). , ( ) ( “” ). 24/2 :

1 + 2 + 3 + 4 + \dots "=" - \frac{1}{12}

$1 + 2 + 3 + 4 + \ldots "=" -\frac{1}{12}$

, D-2=24. :

1 - 2 + 3 - 4 + \dots "=" \frac{1}{4}

$1 - 2 + 3 - 4 + \ldots "=" \frac{1}{4}$

D-2=8. , ( “” ), , , . , - , , . , , , , , — .

−, D-2 = 24? , - 1+2+3+... = -1/12; . , , ζ-, + ( ), , , - . ; , , - “” ? , . ?

, D=26 :

- . / .
- . , , / .
- . .
- . .
- . , .

1.1, . , . 3.1, .

, , . , :

1.2 , , . 2.1 , . 3.2 — , - ( ) , .

, "" ( ), . , , . , .

, — 3.2. , ( ). , . 24 ( 2, 3, 4). 1+2+3+...=-1/12 .

, -. $(\sigma^1,\sigma^2)$ . , , , $(\sigma^1,\sigma^2) \rightarrow (\sigma^{1}\prime,\sigma^2 \prime)$ . , . () /:

(σ^{1}, σ^{2}) \to (λ σ^{1}, λ σ^{2})

$(\sigma^1, \sigma^2) \rightarrow (\lambda \sigma^1, \lambda\sigma^2)$

, , . , , . .

, , -. , — . , , , , . , , $exp(iE_it)$ i, $E_i$ , t. ,

Z = \sum_{i} e^{i E_{i} t}

$Z = \sum_i e^{i E_i t}$

. Z .

, AB A B $Z_{AB} = Z_A Z_B$ . Z , , D-2, D-2.

, , .

, , , . ,

E_{n} = ω (\frac{1}{2} + n)

$E_n = \omega \left( \frac{1}{2} + n \right)$

? , Z

Z_{Q H O} = \sum_{n = 0}^{\infty} e^{i E_{n} t} = e^{\frac{i}{2} ω t} \sum_{n = 0}^{\infty} e^{i n ω t} = \frac{e^{\frac{i}{2} ω t}}{1 - e^{i ω t}}

$Z_{QHO} = \sum_{n=0}^\infty e^{i E_n t} = e^{\frac{i}{2}\omega t} \sum_{n=0}^\infty e^{i n \omega t} = \frac{e^{\frac{i}{2} \omega t}}{1 - e^{i\omega t}}$

, , , |r| = 1, , . : Z, , ( -) . , , , “”, exp(ix), , , - , — , . , , , .

? . , Z . : , t , ( , ). , ; — , - ( , , t Im t > 0.).

, , , , . ω=1,2,3,... Z 1D-

Z_{1, L} = \prod_{k = 1}^{\infty} \frac{e^{\frac{i}{2} k t}}{1 - e^{i k t}} = e^{\frac{i}{2} (1 + 2 + 3 + \dots) t} {(\prod_{k} 1 - e^{i k t})}^{- 1}

$Z_{1,L} = \prod_{k=1}^\infty \frac{e^{\frac{i}{2}k t}}{1- e^{ikt}} = e^{\frac{i}{2} (1+2+3+\ldots)t } \left(\prod_k 1- e^{ikt}\right)^{-1}$

… . 1+2+3+ ... . , 1+2+3+...→-1/12, , . , , 24 . .

? , , — $E_0 = \frac{\omega}{2}$ . , . , , , p, q $\hat p, \hat q$ , “” , pq. $\hat p, \hat q$ ? $\hat p, \hat q$ ? — . , , , :

Z_{1, L}^{- 1} = e^{- i r t} \prod_{k} 1 - e^{i k t}

$Z_{1,L}^{-1} = e^{-irt} \; \prod_k 1 - e^{ikt}$

r — . , r = 1/24. , :

, , 1 / r — .
, , r = 1/24 , 1+2+3+...=-1/12

, t . , :

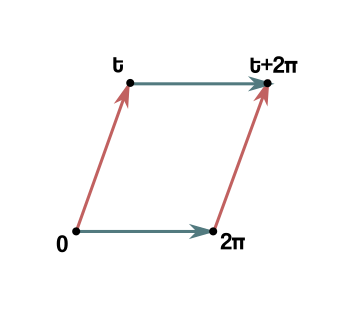
t . ( 2π ω=1,2,3,... ). τ=t/2π (+ , , , ):

, τ . : ? . ( , ).

$q:=e^{i2\pi\tau}$ , $Z_{1, L}$

Z_{1, L}^{- 1} (τ) = q^{r} \prod_{k} (1 - q^{k})

$Z_{1,L}^{-1}(\tau) = q^r \; \prod_k (1-q^k)$

, τ→τ+1,

( !). , .

Z_{1, L}^{- 1} \to e^{2 π i r} Z_{1, L}^{- 1}

$Z_{1,L}^{-1} \rightarrow e^{2\pi i r} \, Z_{1,L}^{-1}$

… , . D−2 $Z^{D-2}_{1, L}$ , ,

r (D - 2) = 1

$r(D-2) = 1$

. 1 / r, D = 1/r+2 - .

, r = 1/24, . , .

, , — τ → -1/τ. , — . , 1 -1 / τ, τ 1. , .

, ; $Z^{D-2}_{1, L}$ . ? $Z^{D-2}_{1, L}$ ? , , . ( ) , . : , , …

, $Z_{1, L}$ (L “”) $Z_{1, R}$ . , , $Z_{1, R} = Z_{1, L}^*$ , $|Z^{D-2}_{1, L}|^2$ .

: “” , . , τ, , ; , , .

, 1D ? , . 1D, , $(time)^{-1/2}$ . , ,

(ℑ τ)^{- 1 / 2}

$(\Im \tau)^{-1/2}$

, ,

Z \sim (ℑ τ)^{- \frac{D - 2}{2}} | Z_{1, L} |^{2 (D - 2)}

$Z \sim (\Im \tau)^{-\frac{D-2}{2}} \, | Z_{1,L} |^{2(D-2)}$

τ→−1/τ:

ℑ τ \to \frac{1}{| τ |^{2}} ℑ τ

$\Im \tau \rightarrow \frac{1}{ | \tau |^2} \Im \tau$

, $Z_{1, L}$ -

Z_{1, L} \to τ^{- 1 / 2} Z_{1, L}

$Z_{1,L} \rightarrow \tau^{-1/2} Z_{1,L}$

, . , , r=1/24.

Z_{1, L}^{- 1} (τ) = q^{r} P (τ), P (τ) := \prod_{ℓ = 1}^{\infty} (1 - q^{ℓ})

$Z_{1,L}^{-1} (\tau) = q^r P(\tau)\,,\quad P(\tau) := \prod_{\ell=1}^\infty (1-q^\ell)$

, P(τ) :

- \log P (τ) = - \sum_{ℓ = 1}^{\infty} \log (1 - q^{ℓ}) = \sum_{l, k = 1}^{\infty} \frac{1}{k} q^{k ℓ} = \sum_{k = 1} \frac{1}{k} \frac{q^{k}}{1 - q^{k}} = \sum_{k = 1} \frac{1}{k} \frac{1}{q^{- k} - 1}

$-\log P(\tau) = - \sum_{\ell=1}^\infty \log(1-q^\ell) = \sum_{l,k = 1}^\infty \frac{1}{k} q^{k\ell} = \sum_{k = 1} \frac{1}{k} \frac{q^k}{1-q^k} = \sum_{k=1} \frac{1}{k} \frac{1}{q^{-k} -1}$

-log(1-x) . , , ( ) Im τ>0.

(, ). w, τ :

f (w) = \cot w \cot \frac{w}{τ}

$f(w) = \cot w \cot \frac{w}{\tau}$

, $\nu$ ( , ),

g (w) = \frac{f (ν w)}{w}

$g(w) = \frac{f(\nu w)}{w}$

g. , w=±nkv w=±nktv, k=1,2,3,...; w=0. :

{Res}_{\pm \frac{π k}{ν}} g = \frac{1}{π k} \cot (\frac{π k}{τ}) {Res}_{\pm \frac{π k τ}{ν}} g = \frac{1}{π k} \cot (π k τ) {Res}_{0} g = - \frac{1}{3} (τ + τ^{- 1})

$\operatorname{Res}_{\pm\frac{\pi k}{\nu}} g = \frac{1}{\pi k}\cot \left( \frac{\pi k}{\tau} \right)\\ \operatorname{Res}_{\pm\frac{\pi k \tau}{\nu}} g = \frac{1}{\pi k}\cot \left( \pi k \tau \right)\\ \operatorname{Res}_{0} g = - \frac{1}{3} (\tau + \tau^{-1})$

( ) , , $\cot s \sim \frac 1 s - \frac s 3$ .

g (w), (τ = i), (ν = 1). — , , .

, g . γ 1,τ,−1,−τ.

\frac{1}{2 π i} \int_{γ} \frac{f (ν w)}{w} d ω = \sum_{p \in poles} {Res}_{p} g

$\frac{1}{2\pi i} \int_\gamma \frac{f(\nu w)}{w} d\omega = \sum_{p \in \operatorname{poles}} \operatorname{Res}_p g$

, , , , .

, , . τ , , Im τ>0. , , τ , , , . , , τ , .

, . $g(w)=f(\nu w)w^{−1}$ , , . , ν→∞. , f(vw) (1,-1,1,-1) γ ( , ). ,

(\int_{1}^{τ} - \int_{τ}^{- 1} + \int_{- 1}^{- τ} - \int_{- τ}^{1}) \frac{d w}{w}

$\left( \int_1^\tau - \int_\tau^{-1} + \int_{-1}^{-\tau} - \int_{-\tau}^{1} \right) \frac{dw}{w}$

! 1/w — log w, … ! ! , .

2 (\int_{1}^{τ} + \int_{1}^{- τ}) \frac{d w}{w}

$2\left( \int_1^\tau + \int_1^{-\tau} \right) \frac{dw}{w}$

, , , , . ,

4 \log (\frac{τ}{i})

$4 \log \left(\frac{\tau}{i} \right)$

. . ν→∞, ; , , . ,

- \frac{1}{3} (τ + τ^{- 1}) + 2 \sum_{k = 1}^{\infty} (\frac{1}{π k} \cot (\frac{π k}{τ}) + \frac{1}{π k} \cot (π k τ))

$-\frac{1}{3} (\tau + \tau^{-1}) + 2 \sum_{k=1}^\infty \left( \frac{1}{\pi k} \cot(\frac{\pi k}{\tau}) + \frac{1}{\pi k} \cot(\pi k \tau) \right)$

\cot s = \frac{e^{i s} + e^{- i s}}{e^{i s} - e^{- i s}} = \frac{1 + e^{- 2 i s}}{1 - e^{- 2 i s}} = - 1 + \frac{2}{1 - e^{- 2 i s}}

$\cot s = \frac{ e^{is} + e^{-is} }{e^{is} - e^{-is} } = \frac{1 + e^{-2is}}{1 - e^{-2is}} = -1 + \frac{2}{1-e^{-2is}}$

- \frac{1}{3} (τ + τ^{- 1}) + \frac{4}{π} \sum_{k = 1}^{\infty} \frac{1}{k} (\frac{1}{1 - e^{- \frac{2 π i k}{τ}}} - \frac{1}{1 - e^{- 2 π i k τ}}) = - \frac{1}{3} (τ + τ^{- 1}) + \frac{2}{π} (\log P (- 1 / τ) - \log P (τ))

$-\frac{1}{3} (\tau + \tau^{-1}) + \frac{4}\pi \sum_{k=1}^\infty \frac{1}{k} \left( \frac{1}{1-e^{-\frac{2\pi i k}{\tau}} } - \frac{1}{ 1- e^{-2 \pi i k \tau} } \right) \\ =-\frac{1}{3} (\tau + \tau^{-1}) + \frac{2}{\pi} \left(\log P(-1/\tau) - \log P(\tau) \right)$

- . P(τ). , , .

\frac{1}{2} \log (\frac{τ}{i}) = - \frac{π i}{12} (τ + τ^{- 1}) - (\log P (τ) - \log (P (- 1 / τ))

$\frac{1}{2} \log\left(\frac{\tau}{i} \right) = - \frac{\pi i}{12} (\tau + \tau^{-1}) - \left(\log P(\tau) - \log(P(-1/\tau) \right)$

! , . , … :

e^{\frac{2 π i / τ}{24}} P (- 1 / τ) = \sqrt{τ / i} e^{\frac{2 π i τ}{24}} P (τ)

$e^{\frac{2\pi i / \tau}{24}} P(-1/\tau) = \sqrt{\tau/i} \; e^{\frac{2 \pi i \tau}{24}} P(\tau)$

, ,

η (τ) := e^{\frac{2 π i τ}{24}} P (τ) = q^{\frac{1}{24}} \prod_{k = 1}^{\infty} (1 - q^{k})

$\eta(\tau) := e^{\frac{2\pi i \tau}{24}} P(\tau) = q^{\frac{1}{24}} \prod_{k=1}^\infty (1-q^k)$

, τ→-1/τ:

η (- 1 / τ) = \sqrt{\frac{τ}{i}} η (τ)

$\eta(-1/\tau) = \sqrt{\frac{\tau}{i}} \eta(\tau)$

! ! $Z^{-1}_{1, L}(\tau)$ , , η(τ), r=1/24, ,

D = 26

$D = 26$

- , , , , (, , ) . η(τ) — , , , ; , $\Delta(\tau):=(2\pi)^{12}\eta^{24}$ 12. ; , , , , . , , , -, .

: , 1+2+3+...=-1/12, ζ- / / , , ?

, .

- “ ” “”, , , . , . , , . , / — . - , , 24. , .

, D=26 ( D=10), , , . , , , .

, ,

P (τ) = \prod_{k = 1}^{\infty} (1 - q^{n}) = \sum_{k = - \infty}^{\infty} (- 1)^{k} q^{k (3 k - 1) / 2}

$P(\tau) = \prod_{k=1}^\infty (1-q^n) = \sum_{k=-\infty}^{\infty} (-1)^k q^{k(3k-1)/2}$

P (τ) = q^{- 1 / 24} \sum_{k = - \infty}^{\infty} (- 1)^{k} q^{\frac{3}{2} (k - \frac{1}{6})^{2}}

$P(\tau) = q^{-1/24} \sum_{k=-\infty}^{\infty} (-1)^k q^{\frac{3}{2}(k-\frac{1}{6})^2}$

η (τ) = q^{1 / 24} P (τ) = \sum_{k = - \infty}^{\infty} (- 1)^{k} q^{\frac{3}{2} (k - \frac{1}{6})^{2}}

$\eta(\tau) = q^{1/24} P(\tau) = \sum_{k=-\infty}^{\infty} (-1)^k q^{\frac{3}{2}(k-\frac{1}{6})^2}$

η $\eta(−1/\tau)=\sqrt{\tau/i}\eta(\tau)$ .

, , .

Simple and rigorous proof of 26/10 dimensions in string theory

More articles: