First, let us turn to the well-known and familiar electronic signature algorithm, which is widely used in information systems for various purposes. The electronic signature is based on asymmetric cryptographic algorithms. Asymmetric encryption is encryption using 2 keys: one is used for encryption, the other is used for decryption. They are called public (public) and private keys. The public key is known to others, while the private key is known only to the owner of the electronic signature and is stored in a place inaccessible to others.
When signing, the following happens: first, an electronic document, using mathematical transformations, is reduced to a sequence of characters of a certain size - this is called a hash function.
The received character sequence (hash from the document) is encrypted by the sender of the document using the private key and, together with the public key, is sent to the recipient. The recipient decrypts the character sequence using the public key, applies the exact same hash function to the document, and compares the conversion result with the decryption result. If everything matches, then no changes were made to the document after it was signed by the sender.
The described actions allow you to make sure that the document has not changed, but they do not allow you to verify that the sender is really who he claims to be. Therefore, we need a third party that is trusted by both the sender and the recipient. To do this, before sending the document, the sender contacts a third party and asks her to sign his public key with her electronic signature. The sender now sends the document, his public key, and a third party signature to his key to the recipient. The recipient verifies the third party signature of the public key and trusts the received document signature.
Now let's move on to what a "blind signature" is and how it can help us with anonymization.
Imagine that in the example described above, the sender is the voter, the document is the ballot, and the recipient is the electoral commission, or as we said "the component of accounting and counting of votes." As a third party (validator) we will have the "Voter List" component. In this case, the process can proceed as follows.
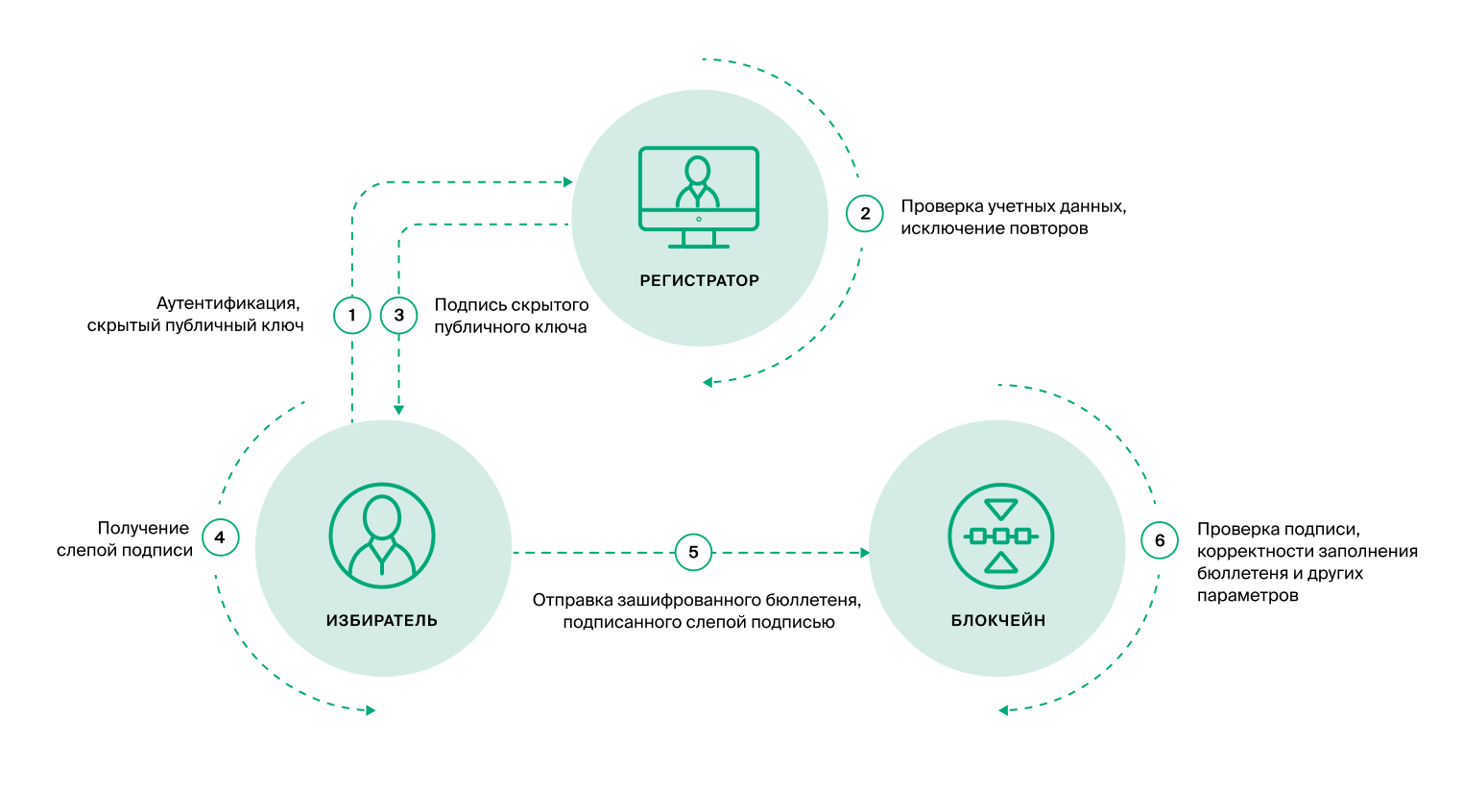
The voter on his device generates a pair of keys - private and public. Since these keys are generated on his personal device in the browser, they are known only to him.
With these keys, he will sign the ballot to control its integrity. He sends the signed ballot and the public key to the election commission. In order for a ballot to be accepted by the Distributed Storage and Counting Component, it must verify that the public key is signed by the validator.
The validator (“Voter list” component) will sign the public key only after making sure that the voter is on the voter list.
To solve the problem of keeping the secrecy of voting, the voter's public key, created on his device, should not be known to anyone. It turns out that the validator must sign what is unknown to him. The task seems impossible, but here cryptographic algorithms come to the rescue - in this case, the "blind signature" algorithm
First, the public key must be masked on the voter's device. Masking is the execution of individual mathematical actions on the user's device. Imagine that you conceived some random number from 1 to 100, then conceived a second random number from 1 to 10 and a third, from 10 to 50, the originally conceived number was raised to the power of the second number, and divided without a remainder by the third. The result was communicated to others. It will not be difficult for you to restore the original number, since you know the sequence of actions and the numbers you have conceived. But those around them will not be able to do this.
Masking (blinding) of the public key is performed according to a special cryptographic algorithm. As a result, the validator signs the masked public key without knowing the original key. But the peculiarities of the algorithm are that the user (voter), having received a signature on a masked key, can make inverse transformations and get a signature valid for the original, unmasked key.
The described algorithm is widely used in secret voting protocols. The remote electronic voting system currently uses the RSA algorithm with a key length of 4096 bits for blind signature.
In general, the anonymization procedure is as follows.
- «», . .
- ( , ), .
- « » .
- – , .
- « »
- ,
- If all checks are successful, the key is signed
- The fact of the key signing is recorded in the blockchain
- The user on his device removes the mask from the public key and receives a private key, a public key and a signature on the public key, while all the keys are known only to him.
- After that, the user is transferred to an anonymous zone - to a separate site edg2020.gov.ru, where it is impossible to identify him (for example, before the transition, he can connect a VPN or change the Internet provider by completely changing the IP address)
- Acceptance of the ballot will depend only on whether the signature of the "validator" is verified and whether such a key has been used earlier.
Below is a description of the algorithm in terms of cryptography.
Signature and designation parameters:


M - in the FDN padding format for the signature.