Powerful SAT solver technology can work with the infamous Collatz hypothesis. However, the chances of this are not very high.

In the past few years, Mariin Hijul has used a computerized proof-finding technology called SAT solver (SAT for satisfiability) to conquer an impressive list of mathematical problems. Pythagorean triplets in 2016, Schur's number 5 in 2017, and recently Keller's hypothesis in the seventh dimension, which we wrote about not so long ago in the article " Computer search helped to deal with a 90-year-old mathematical problem ."
Now, however, Hijul, a computer scientist at Carnegie Mellon University, has set his sights on an even more ambitious goal: the Collatz conjecture, considered by many to be the most difficult open problem in mathematics (and arguably the simplest to formulate). Other mathematicians, learning from me that Khiyul was making such an attempt, were skeptical about it.
“I don’t see how this problem can be solved completely with the SAT solver,” said Thomas Hales of the University of Pittsburgh, a leading expert in computer evidence. This technology essentially helps mathematicians solve problems - some of which have an infinite number of options - by turning them into discrete, finite problems.
However, Hales, like the others, was wary of underestimating Khiyul. “He is very good at finding clever ways to formulate problems in the SAT language. He's very good at it. "
Scott Aaronsonfrom the University of Texas at Austin, working with Hiyul on the Collatz conjecture, added: “Marin is a man with a hammer, that is, with a SAT solver, and is probably the most worthy bearer of this hammer in the entire world. And he tries to apply it to almost everything. " But only time will tell if he can turn the Collatz hypothesis into a nail.
The SAT solution requires reformulating the problems in a computer-understandable language that uses propositional logic , and then connecting computers to decide if there is a way to make these statements true. Here's a simple example.
Let's say you are a parent trying to arrange childcare. One of your nannies may work all week except Tuesday and Thursday. The other is apart from Tuesday and Friday. The third - except Thursday and Friday. You need to sit with your child on Tuesday, Thursday and Friday. Can this be achieved?
One way to test this is to turn the nanny constraints into a formula and feed it to the SAT solver. The program will look for a way to distribute the days among the nannies so that the formula turns out to be true, or "satisfied" - that is, so that you get the three days you need. If successful, such a method will exist.
Unfortunately, it is not immediately clear how to reformulate many of the most important mathematical questions into SAT language. But sometimes they can be rephrased as satisfaction questions in unexpected ways.
“It's hard to predict when the task will be reduced to a huge but finite computation,” said Aaronson.
The Collatz conjecture is one of those math questions that at first doesn't seem like a nanny problem at all. She suggests the following: take any number (integer, non-zero). If it's odd, multiply it by 3 and add 1. If it's even, divide by 2. As a result, you get a new number. Apply the same rules to it and continue. The hypothesis predicts that regardless of the starting number, you end up with 1, and then you get stuck in a loop: 1, 4, 2, 1.
And, despite the fact that this hypothesis has been worked for almost 100 years, mathematicians have not come close to proving it.
But this did not stop Khiyul. In 2018, he and Aronson - while being university colleagues - received a grant from the National Science Foundation to apply the SAT solver to the Collatz conjecture.
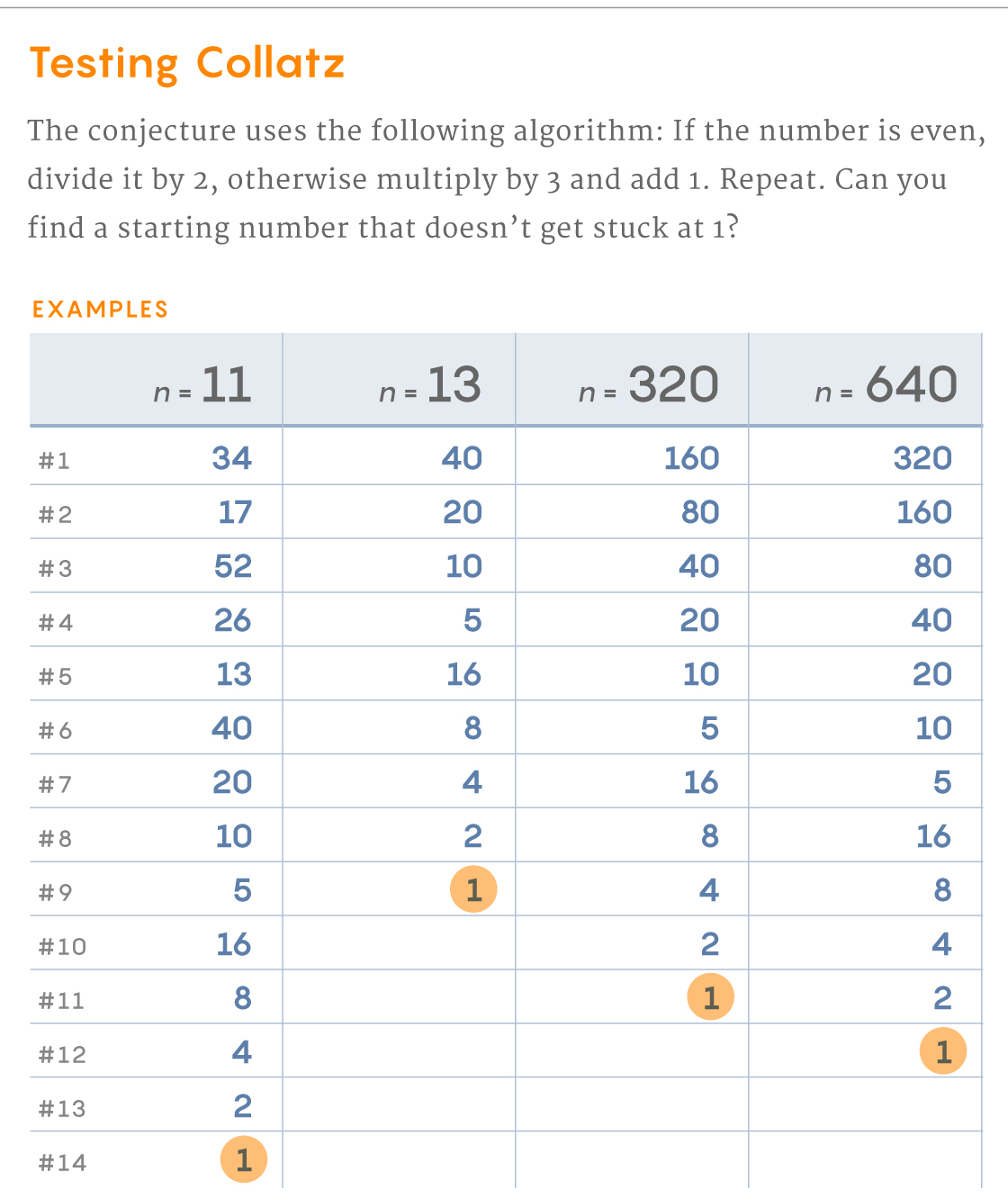
Take any number. If it's odd, multiply it by 3 and add 1. If it's even, divide by 2. As a result, you get a new number. Apply the same rules to it and continue. Can you find a number that doesn't lead to 1? You can try it yourself .
To begin with, Aaronson, a computer scientist, came up with an alternative formulation of the Collatz hypothesis, the so-called. A "substitution rule system" that made it easier for computers to work with.
In a substitution rule system, you work with a set of characters, such as the letters A, B, and C. You use them to form sequences: ACACBACB. You also have rules for converting these sequences. One rule may say that when you meet an AC, you replace it with BC. Others can replace the aircraft with AAA. You can define any number of rules that define any transformations.
Computer scientists generally need to know if a given JV always ends up. That is, regardless of which line to start with and in what order to apply the rules, is it true that the line will eventually turn into a state in which no rules can be applied?
Aaronson came up with an SP with seven symbols and 11 rules, similar to Collatz's hypothesis. If they can prove that his JV always finishes, they will thereby prove that the hypothesis is correct.
To turn Collatz's hypothesis into a SAT-solver problem, Aaronson and Hiyul had to take another step involving matrices, or arrays of numbers. They needed to assign a unique matrix to each symbol in their SP. This approach - a common way of looking for proof that the SP is finishing work - would allow them to reason about number transformations through matrix multiplication. Seven matrices denoting seven symbols with SP had to satisfy a whole set of constraints, reflecting the correspondence of 11 rules to each other.
“First, you try to find matrices that satisfy these constraints,” saidEmre Yolchu , a PhD student at Carnegie Mellon University, working on this problem with Hijul. “If you succeed, you prove that execution stops,” and therefore that Collatz's hypothesis is correct.
The SAT solver can answer the question of the existence of matrices satisfying these constraints. Aaronson and Hijul first ran the SAT solver on small 2x2 matrices. They did not find working options. Then they tried 3x3 matrices. And again to no avail. They continued to increase the size of the matrices in the hope that they could be found.
However, this approach cannot evolve indefinitely, since the complexity of searching for suitable matrices grows exponentially with their size. Hijul suggests that modern computers simply cannot handle matrices larger than 12x12.
“When the matrices get too complex, you can't solve the problem,” he said.
Hijul is still working on optimizing the search, trying to make it more efficient so that the SAT solver can check larger and larger matrices. She and her colleagues are working on an article summarizing their current discoveries, but they are almost out of ideas and will probably have to give up soon - at least for a while.
After all, the attraction of the SAT solver is that if you could only figure out how to check another case, call another nanny, extend the search even for a little while, you could probably find what you were looking for. In this sense, Khiyul's main advantage may not be his experience with SAT solvers, but his love for the pursuit of results.
“I'm just an optimist,” he said. "I often feel like I'm lucky, so I just try and see how far I can get."