Stephen Wolfram: we seem to be close to understanding the fundamental theory of physics, and it is beautiful

In continuation of my post about the computable Universe, I want to present to you my translation of an article by Stephen Wolfram, created as part of his The Wolfram Physics Project .

Unexpected discovery

Over the past few centuries, there has been a real breakthrough in our knowledge of the principles of the world around us. But despite this, we still do not have a fundamental theory of physics, and we still do not have an answer to the question of how exactly our Universe works. I have been dealing with this topic for about 50 years, but only in the last few months have all the pieces of the puzzle finally started to fit together. And the resulting picture turned out to be much more beautiful than anything I could only imagine.



In those days, when I earned my living as theoretical physics, I did not really think about the search for the so-called "theory of everything." I was more concerned with learning something new from the theories we already have. And I thought that even if someday there was a unified fundamental theory of physics, it would inevitably turn out to be very complex and confusing.



But when I began to study the theory of cellular automata in the early 1980s, I realized that systems operating by even very simple rules can have amazingly complex behavior. And this gave me the thought: could the universe be arranged in a similar way? Maybe under all the seeming complexity and versatility of our Universe, there are very simple rules?



In the early 90s, I had some understanding of what these rules might look like, and towards the end of that decade, I began to understand how from these simple rules we can deduce our knowledge of space, time, gravity and all other physical phenomena. I devoted about 100 pages to these ideas of "calculating" the laws of physics in my book A New Kind of Science .



I've always wanted to start a big research project to move further in this direction. I tried to start a project like this in 2004, but got really caught up in the Wolfram Alpha and the Wolfram Language. From time to time I met with my physics friends and we discussed my ideas. These were interesting conversations, but it seemed to me that the search for a fundamental theory of physics was too difficult a task, available only to really enthusiastic fanatics.



There was something that really bothered me about my ideas. The rules of my theory seemed too inflexible and far-fetched to me. As the creator of a language for mathematical computing, I constantly thought about abstract rule systems. And very often I had the feeling that something similar could be in physics. But my reasoning never got me anywhere. Until all of a sudden in the fall of 2018, I had an interesting idea.



In a sense, this idea was simple and obvious, albeit very abstract. But she was also very elegant and minimalistic. It seemed to me that I was very close to understanding how our universe works. Unfortunately, I was terribly busy developing Wolfram Alpha, and could not find time for another project. Everything changed when, at our annual summer school in 2019, I met two young physicists, Jonathan Gorard and Max Piskunov, who inspired me to finally sit down to work out my ideas. Physics has always been my passion, and after my 60th birthday in August 2019, I finally decided to do it.



So, together with two young physicists who inspired me, we started our project in October 2019. And not having time to start our research, we immediately began to come across very interesting finds. We have replicated everything I developed in the 90s, but in a much more elegant way. From small, structureless rules we have deduced space, time, relativity, gravity, and hints of quantum mechanics.



We've run millions of experiments, testing our guesses. Gradually, everything began to clear up, we began to roughly understand how quantum mechanics works. We understood what energy is. We deduced the formulation of quantum theory in terms of path integralsby my late friend and teacher Richard Feynman. We have seen some deep structural connections between relativity and quantum mechanics. Everything fell into place. We began to understand not only how the laws of physics work, but also why.



I could not even dream that our progress would be so rapid. I expected that our research would go much slower, that if we were lucky, we would slowly advance in understanding the laws of physics and what happened to our Universe in the first seconds of its existence, and that we would spend many years on this research. In the end, if we have a complete fundamental theory of physics, we can find a specific single formula for our universe. And even now I don't know how long it will take: a year, a decade, or even a century. Several months ago, I wasn't even sure we were on the right track. But today everything has changed. Too much fell into place. We do not yet know the exact details and how exactly the gears of our world are configured, but I am completely sure that the model we have will one day tell us abouthow the universe works.



The surest sign of the quality of a scientific model is that simple laws explain complex effects. And our theory, like no other, conforms to this rule of thumb. From the simplest formulas we get whole sections of modern physics. And what is most surprising - we have not yet had to enter any additional parameters for this. We are simply looking for an explanation of physical phenomena in the very properties of our model, without adding anything beyond that.



Our model is based on as simple rules as possible. It's funny how these rules can be written in one line in the Wolfram Language. In their raw form, they are not very similar to all the mathematical structures we know. But once we look at the results of the multi-iterative recursive application of these rules, it becomes clear how elegantly they relate to modern mathematics. It's the same with physics. The basic structure of our models looks completely alien to everything that has been done in physics over the past few centuries. But what we got from our models was amazing: we found that many of the theories that physicists have created in recent decades fit perfectly into our model.



I was afraid that I would have to throw out all the existing achievements of science. But it turned out that despite the fact that our model, approach and methods are very different from all existing ones, our theory is based on everything that physicists have been working on for the past decades.



Then we will start physical experiments. If you had asked me a couple of months ago when we get any testable conclusions from our models, I would answer that it will not be soon and definitely before we find the final formula. But now it seems to me that I was wrong. And in fact, we have already received some guesses about the unexplored bizarre phenomena, the existence of which can be experimentally confirmed.



What's next? I'll be happy to say that I think we have found our way to a fundamental theory of physics. We have built a paradigm, framework and computing tools for it. But now we have to finish the job. We have to do the hard work of physics, mathematics and algorithmic calculations and find out if we can finally answer the question of how our universe works for millennia.



I want to share this exciting moment with you. I am looking forward to many people to participate in our project. This project is not only mine and my little team. This is an important project for the whole world. And when we finish it, it will be our greatest achievement. Therefore, I want as many people as possible to participate in it. Yes, there is a lot to do that requires non-trivial knowledge of physics and mathematics, but I want to spread the word about the project as widely as possible so that everyone can contribute and be inspired by what will be the greatest intellectual adventure in history.



We are officially launching our Wolfram Physics Project... Starting today, we will broadcast everything we do and share our discoveries with the world in real time. I publish all our materials and all our software for calculations. We will be posting reports of our progress and various educational materials on a regular basis.



We also publish the Register of Wonderful Universes for public access . It is filled with about a thousand rules. I do not think that even one of them applies to our universe, although I cannot be completely sure of this. But one day, and I hope that one day it will come very soon, a rule will appear in our registry that completely describes our Universe.

General principles

So how does our model work? I wrote a 448-page technical summary of our ideas (yes, I've done a fair amount of work over the previous few months). Another member of our team, Jonathan Gorard, has written two 60-page technical articles . Several more materials on this topic are available on the page of our project. But in this article I am going to give a brief summary of the general provisions of our theory.



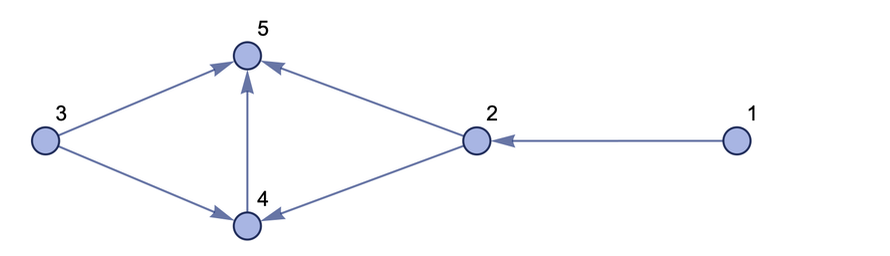
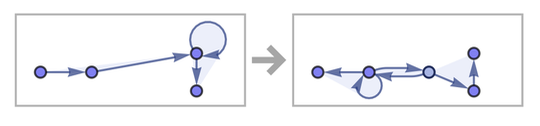
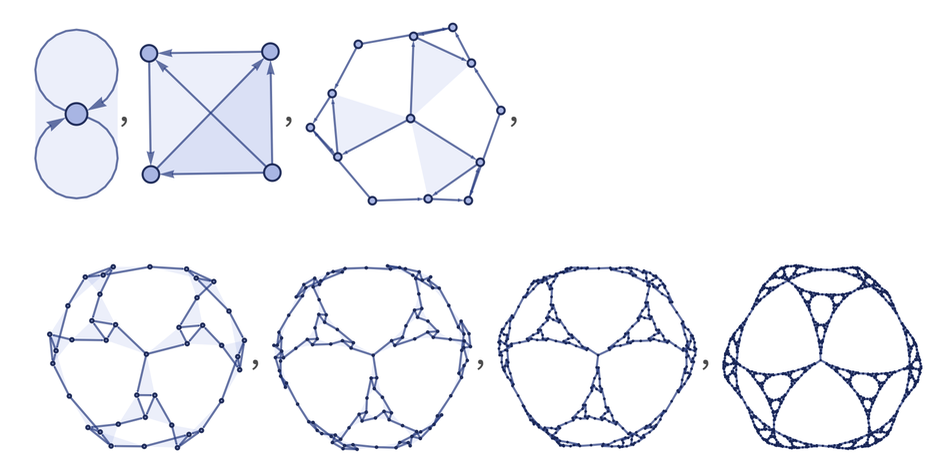
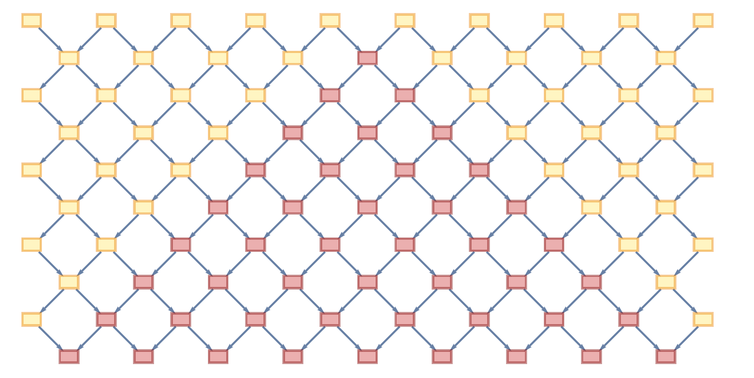
It all starts with the simplest set of abstract relationships between abstract elements, which can also be represented as a graph.



Suppose we have a set of relations:

{{1, 2}, {2, 3}, {3, 4}, {2, 4}}

which in the form of a graph looks like this:





All we define here is relationships between elements (eg {1, 2}). The order in which we declare these relationships is not important, but the order of the elements within each relationship is important. And when sketching a graph, only what is connected with what matters. The actual arrangement of the elements in the picture was chosen only for reasons of beauty and nothing else. It also doesn't matter what the elements are called. I numbered them in the pictures, but I could not have done this.



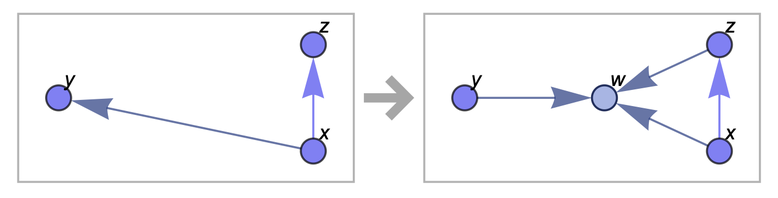
So what are we going to do with these graphs? We will apply a very simple rule to them over and over again. Here's an example of a similar rule:

{{x, y}, {x, z}} → {{x, z}, {x, w}, {y, w}, {z, w}}

This rule says that we should take two relations from the set and check them against the pattern {{x, y}, {x, z}}. If there is a match, then we replace these two relations with the four relations {{x, z}, {x, w}, {y, w}, {z, w}} (where w is a new element of the set).



We can think of this transformation as an operation on graphs:



Now let's apply this rule to our set:

{{1, 2}, {2, 3}, {3, 4}, {2, 4}}

Relations {2,3} and {2,4} match our pattern, so we replace them with four new relationships and get:

{{1, 2}, {3, 4}, {2, 4}, {2, 5}, {3, 5}, {4, 5}}

We can represent the result in the form of a graph (I drew it upside down in relation to the original):



What if we continue to apply this rule to our set recursively? The result will look like this:



Let's do this a couple more times and get a bigger picture:





What happened? We had a very simple rule. But the recursive application of this rule has produced a structure that looks very complex. Common sense tells us that this does not happen. But in reality, this spontaneous inception of complexity is found everywhere when the simplest rules are applied to the simplest structures. My entire book A New Kind of Science is about this phenomenon and why the study of this phenomenon is critical to modern science.



It is from such simple structures and rules that we will derive the principles of our Universe and everything that is in it. Let's take another look at what we have done. We took a simple set of abstract relationships and applied a simple transformation rule to it recursively. But what we received cannot be called simple. And most importantly, a certain shape becomes noticeable in the resulting object. We didn't put any meaning in this form. We just took the simplest rule, and using this rule, we built a graph. When we render this graph, we see that it takes on a certain shape.



If we exclude all matter in the universe, then it turns out that our universe is just a huge chunk of space. But what is space? We've had mathematical abstractions of space for over two thousand years. But what is this space? Does it consist of something, and if so, what exactly?



I think that space looks like the pictures above - it's a whole bunch of abstract points connected to each other. Only in the picture above there are only 6704 points, whereas in the real Universe there are about 10^400or even more.

All possible rules

We do not yet know the exact rule that reflects our universe - and this is definitely not the rule that we just considered. So let's discuss what possible rules are, and what comes out of them.



A characteristic feature of the rule that we considered above was that it works with sets of binary relations containing pairs of elements (for example, {1, 2}). But the same system can work with relationships containing more elements. For example, a set of two ternary relations:

{{1, 2, 3}, {3, 4, 5}}



We cannot represent this set in the form of an ordinary graph, but we can use a hypergraph - a construction in which we generalize the edges of the graph that connect pairs of points into hyper-edges that connect any number of points:



Note that we are dealing with directed hypergraphs, where the order in which the points in the hyper edge are found matters. In this picture, “membranes” simply mean which points are connected to one hyper-edge.



We can set rules for a hypergraph in the same way:

{{x, y, z}} → {{w, w, y}, {w, x, z}}





And this is what happens if we apply this rule to the simplest possible ternary set {{0,0,0}}:





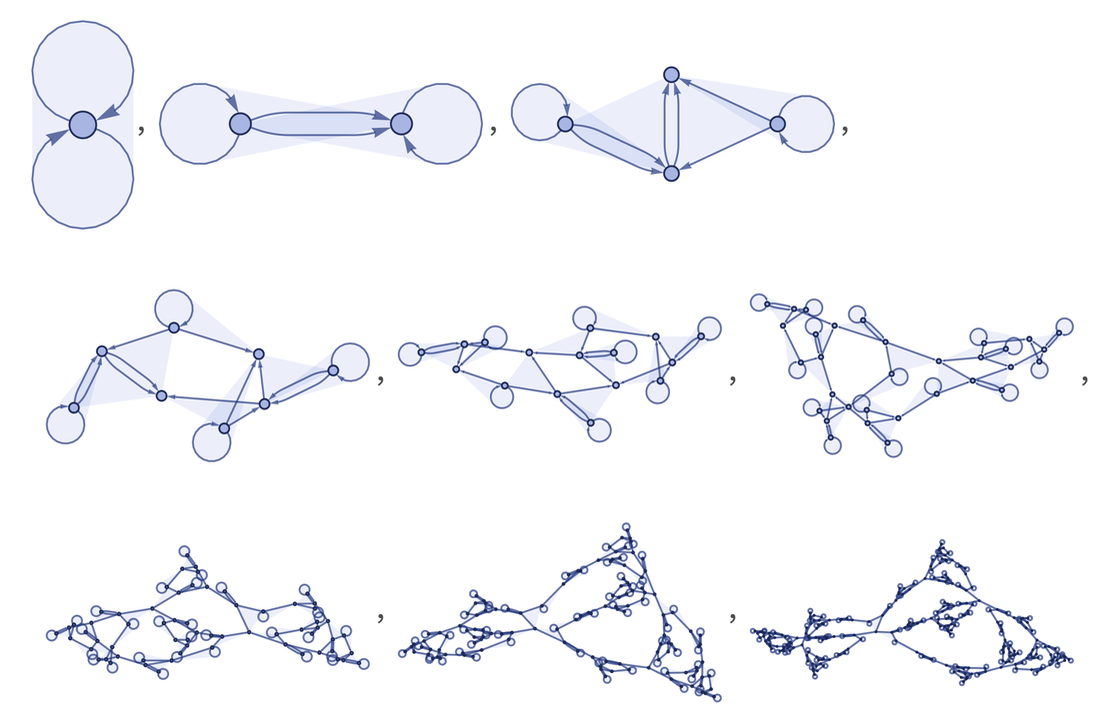
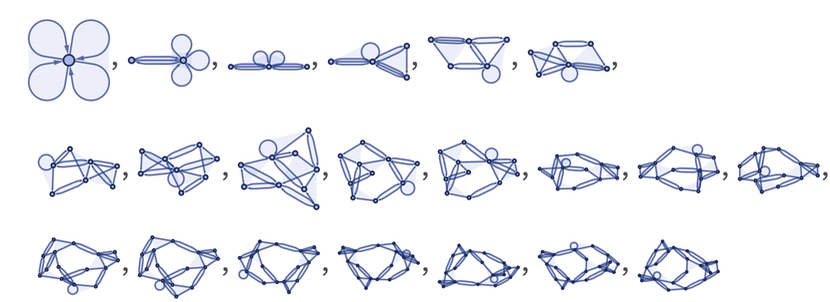
Great! In this case, what happens if we start running different random simple rules? Here are some of the results from these launches:



Don't you think that all these structures look very "alive"? And yes, some of these models can definitely be related not only to fundamental physics, but, for example, to the construction of biological cells. In fact, we see various general forms of behavior here. Some of them are simple, some are not very.



Here are examples of the types of structures that we see:





The main question is: if we run these rules long enough, will they give us a result that reproduces our physical universe? Or, to put it differently, can we find our physical Universe in this mathematical structure computable by simple rules?



And even if our physical Universe is present there, how can we be sure of this? Everything we see in the pictures above is the result of several thousand iterations. In our present Universe, about 10^500iterations have been performed , and maybe even more. Overcoming this difference is not easy. And we must go to the solution of this problem from both sides. On the one hand, we must use all our knowledge about the physics of our Universe, which we have received over the previous several hundred years. On the other hand, we must study these very simple rules for transforming graphs and understand what exactly they do.



And even here there is a potentially fundamental problem: the phenomenon of computational irreducibility. One of the greatest achievements of mathematics happened about three centuries ago: equations and formulas were invented that told how a system behaves without describing every step that the system takes. But many years ago I realized that in a computable universe it is very often impossible to do this. Even if you know the exact rule by which the system works, you cannot understand how the system works without performing each step of the calculation.



You might think that if we know the rule that the system follows, then using all the computing power of our computers and brains, we can always jump ahead and understand how the system will behave. But in reality, this is hampered by an empirical law, which I call the Principle of Computational Equality - in almost any case, when the behavior of the system is not obviously simple, then there is no algorithm for calculating the state of the system after a certain number of iterations with a computational complexity less than the computational complexity of implementing all these iterations ... So we cannot "overtake" the computation, and to understand how the system works, we have to perform an irreducible number of steps.



This could potentially be a big problem for our models. Because we cannot even come close in terms of the number of iterations performed to the number of iterations that our Universe has made since the beginning of its existence. It is also not entirely clear whether we can extract enough information from running our models on the computing power available to us and understand how this information relates to the laws of physics we know.



The biggest surprise for me was that we seem to be lucky. We know that even when our system has computational irreducibility, it also has an infinite number of zones of computational reducibility. And most of these zones correspond to our knowledge of physics.

What is space?

Let's take a look at one simple rule from our huge collection:

{{x, y, y}, {z, x, u}} → {{y, v, y}, {y, z, v}, {u, v, v}}





This is what it generates:



And after a few more iterations you get this:



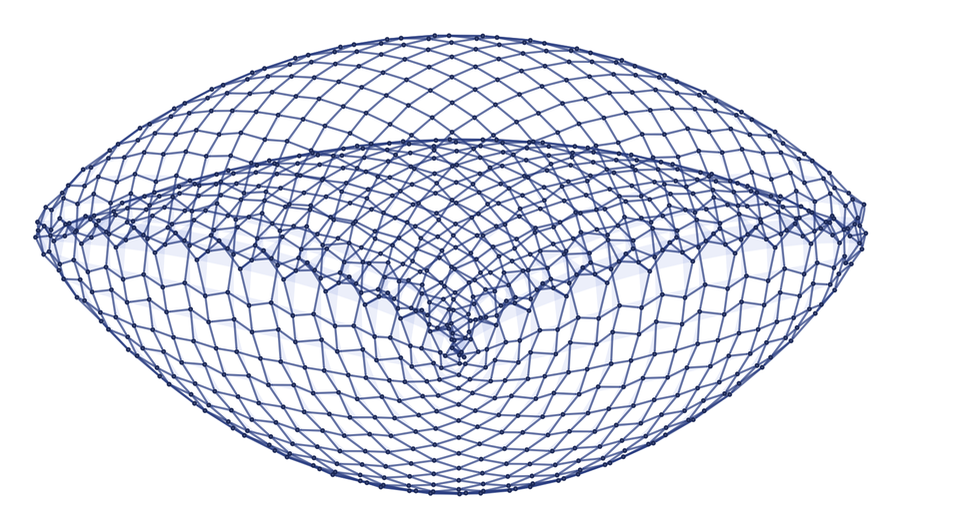
The resulting structure strongly resembles a very simple "piece of space". If we continue to recursively apply our rule further, then this mesh will become thinner and thinner, until it eventually becomes indistinguishable from a solid plane.



Here's another rule:

{{x, x, y}, {z, u, x}} → {{u, u, z}, {v, u, v}, {v, y, x}}







This structure already looks like three-dimensional. And here's another rule:

{{x, y, z}, {u, y, v}} → {{w, z, x}, {z, w, u}, {x, y, w}}







Doesn't that seem strange to you? We have a rule that defines how to rewrite pieces of an abstract hypergraph without any reference to geometry or 3D space. And after a certain number of iterations, this rule generates a hypergraph that looks like a 3D surface.



And despite the fact that in reality there are only connections between points, we can "guess" what shape such a surface can be and render the result in three dimensions:



As we continue, the mesh will gradually get thinner and thinner until it turns into a continuous 3D surface that you could study in a calculus course. Of course, in some way this is not a "real" surface - it is just a hypergraph representing a bunch of abstract relationships, but somehow the pattern of those relationships makes the structure more and more like a surface.



And I think that this is how all space in our Universe is arranged. Basically it's a bunch of discrete, abstract relationships between abstract points. But when viewed from a certain scale, we see that the pattern of these relationships makes this structure similar to the continuous space we are used to. This is similar to our idea of ​​water: in fact, water is a bunch of discrete molecules, but when we look at it from a large scale, it seems to us to be a continuous liquid.



People have been thinking that space can be discrete since antiquity, but no one has succeeded in writing this concept into modern physics. And it is much more convenient to consider space as a continuum so that it is possible to use all the power of the mathematical apparatus we have created. But now it seems to me that the idea that space is discrete will definitely enter into the fundamental theory of physics.

Dimension of space

We perceive space as three-dimensional. How can our rules reproduce this three-dimensionality? The two rules that we just looked at gave rise to two-dimensional surfaces: in the first case, it is flat, in two it has a certain shape. Of course, these are not very honest examples of two-dimensional space - they are just meshes that we recognize as surfaces. With our Universe, things are different, it is much more complicated.



Let's then consider this case:





If we continue to apply the rule that created this picture many more times, will we get something like a space, and if so, how many dimensions will such a space have? To answer this question, we must define a non-objectionable way of defining the number of dimensions. But remember, the pictures I've drawn are just a visualization of a structure that is a bunch of discrete relations or a hypergraph without any information about coordinates, geometry or even topology. Separately, I emphasize that this graph can be drawn in a bunch of different ways:





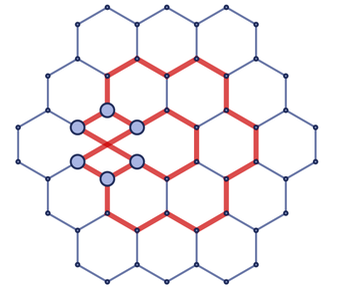
In order to determine the number of measurements, we need to remember that the area of ​​a circle is calculated as πr ^ 2 , and the volume of a sphere as 4/3 π r ^ 3... In general, the "volume" of a d-dimensional analog of a sphere is equal to a constant multiplied by r ^ d . Let's go back to our hypergraph and pick a random starting point. Then we outline the r hyper edges in every possible way. Thus, we have an analogue of a "spherical ball" on a hypergraph. Here are examples of hypergraphs corresponding to 2D and 3D spatial grids:







And if you count the number of points reached by the stroke with "graph radius r", you will find that their number in these two cases grows as r ^ 2 and r ^ 3, respectively. This gives us a way to define the dimension of our hypergraph. We just start at a certain point and see how many points we can reach by drawingr edges:





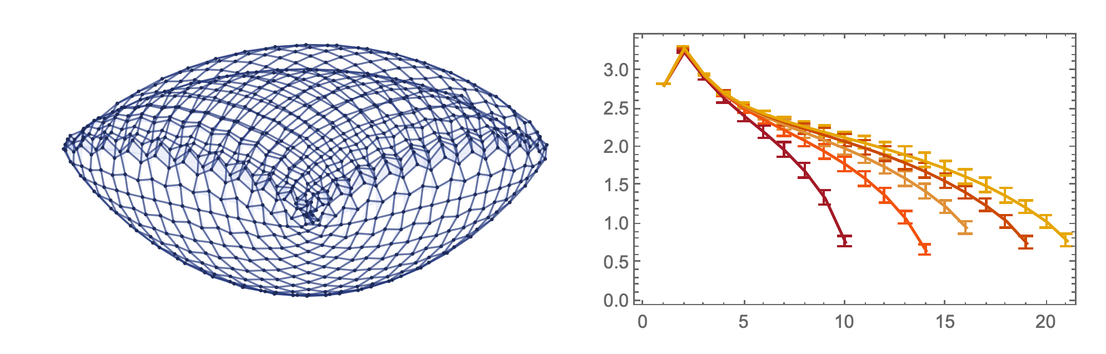
Now, to determine the exact value of the number of measurements, we need to correlate the resulting result with r ^ d . It should be borne in mind that you should not take too small r , at which the structure of the graph can greatly affect the result, or too large r , at which we can run into the edge. We also have to consider how this "space" evolves with each iteration. Given these limitations, we can run a series of calculations to accurately determine the measurements. After calculating for the example we are considering above, we get the number of measurements approximately equal to 2.7:



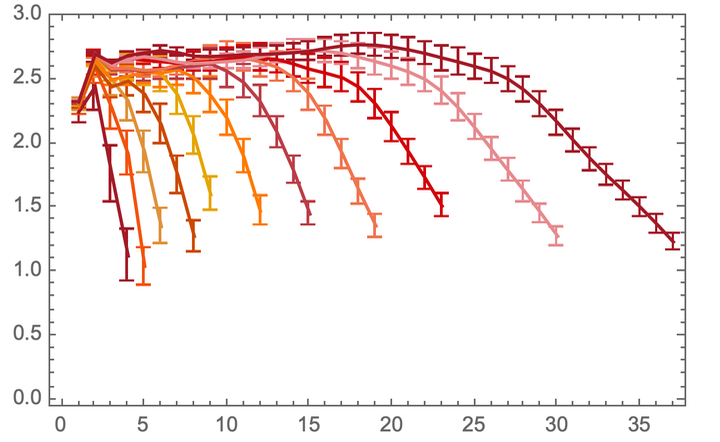
If we do the same for this graph here: The



number of measurements tends to 2, as it should:





But what does the non-integer value of the number of dimensions mean? Let's look at fractals that we can easily create using this rule:

{{x, y, z}} → {{x, u, w}, {y, v, u}, {z, w, v}}





If we measure the number of dimensions for this fractal, we get log2 (3) = 1.58 - an ordinary non-integer measurement for the Sierpinski triangle:



The rule we are considering above does not produce the same even structure like this. In fact, even if the rule itself is completely deterministic, the structure it generates may be completely random in shape. But our measurements suggest that given enough iterations, this rule produces something like 2.7-dimensional space.



Of course, 2.7 is not 3, and apparently this particular rule is not the rule of our Universe (although it is not known how many dimensions this space will get if we run this rule at least 10^100iterations). But quantifying dimensions provides an example of how we can begin to make physical assumptions about the behavior of our rules.



By the way, we talked about the "appearance of space" in our models, but in reality this way not only space appears, but everything else that is in the universe. In modern physics, space is described in a variety of ways and serves, so to speak, as a background for everything else: matter, particles, planets, and so on.



But in our models, in a sense, there is nothing but space: that is, everything in the Universe must "consist" of space. Or, to paraphrase, the same hypergraph that generates space also generates everything else that exists in this space. This means that, for example, a particle like an electron or a photon must correspond to some simple property of a hypergraph. As in this toy example:





According to my estimates, the 10^200hypergraph spends many times more forces on "supporting" the structure of space than on "supporting" all matter existing in the Universe.

Space curvature and Einstein's equations

Here are some simple examples of some of the structures that our rules generate:





They all look like surfaces, but they are obviously different. And the only way to somehow characterize them is by their local curvature. It turns out that in our models, curvature is a concept closely related to the number of dimensions. This fact is critical for understanding, for example, why gravity occurs.



But first, let's talk about how you can measure the curvature of a hypergraph. Usually the area of ​​a circle is equal. πr^2But let's imagine that we have drawn a circle on the surface of a sphere and now we are trying to find its area:



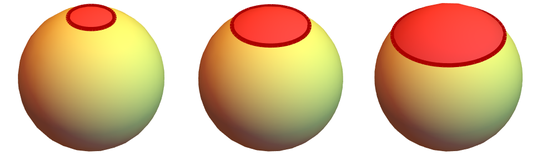
Now the area is not equal πr^2. Instead, it is calculated using a formula πr^2 \* (1 - r^2/12a^2 + r^4/360a^4 - ...)in which aIs the radius of the sphere. In other words, the larger the radius of the drawn circle becomes, the more its area is affected by the fact that it is drawn on the surface of a sphere. Imagine a circle drawn on a globe around the North Pole — the largest possible circle will be at the equator.



If we generalize this formula for d dimensions, we get the following formula for the growth of "volume":, r^d(1-Rr^2/6(d+2)+...)where R is a mathematical object called the scalar Ricci curvature .



This means that if we consider the growth rate of spherical balls in our hypergraph, we can expect two matches: firstly, this speed corresponds r^d, and secondly, the "correction" of this speed due to curvature is equal to r^2.



Here's an example. Instead of estimating the number of measurements (in this case equal to 2), we describe a smoothly descending variable corresponding to the positive (like a sphere) curvature of the surface:





But what is the value of the curvature? First, it has applications in geodesy. A geodetic line is the shortest distance between two points. In flat space, it is a straight line, but in curved space, geodesic lines are also curved:





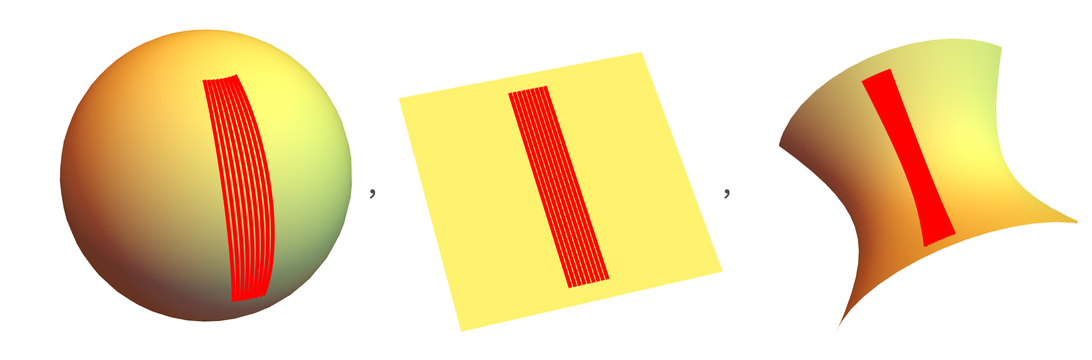
In the case of positive curvature, the bundles of geodesic lines converge, in the case of negative curvature they diverge. Even though geodesic lines were originally defined for continuous space, they can also be present in graphs. For graphs, the definition of a geodesic line is exactly the same - it is the shortest path between two points on the graph.



Here are geodesic lines on a positively curved surface generated by one of our rules:



Here are geodesic lines in a more complex structure:





Why are these geodesic lines so important? The reason is that in Einstein's general theory of relativity, light travels along a path corresponding to geodesic lines. And gravity in this theory is related to the curvature of space. That is, when something deviates from its trajectory around the Sun, it is because the space around the Sun is curved and the geodesic line of this object is also curved.



The description of the curvature of space in general relativity is based on the scalar Ricci curvature R, which we talked about above. But if we want to understand how our models reproduce Einstein's equations for gravity, we must find out that the Ricci curvature obtained from our hypergraphs corresponds to the curvature assumed by the theory of relativity.



Here we have to resort to a little mathematical research (for example, we will consider the curvature of space-time, not just space). In short, within varying limits and under certain assumptions, our models do indeed reproduce Einstein's equations. We first reproduce the equations for a vacuum without matter. Then, when we discuss the nature of matter, we will see that we actually get the complete Einstein equations.



It is a very difficult task to reproduce Einstein's equations. Usually in physics everything starts with these equations, but here they appear from the properties of the model itself.



I think it's worth explaining a little about how this output works. This is something similar to the derivation of the equations of fluid flow from the equations of dynamics of the set of discrete molecules of which this fluid is composed. In our case, we are calculating the structure of space rather than the speed of the fluid. Although for this we need to make a number of very similar mathematical approximations and assumptions. Suppose, for example, that the randomness in the system is good enough for statistics to be well applied to. There are also a bunch of tricky mathematical constraints. For example, the distances should be huge compared to the length of the edge of the hypergraph, but small enough compared to the overall size of the graph, and so on.



Quite often physicists "hammer" on mathematical subtleties. For example, this continued for about a century in the case of deriving fluid flow equations from molecular dynamics. And we can be accused of the same. In other words, there is still a lot of mathematical work to be done in order for our conclusion to be really rigorous and thorough, and we would exactly understand its limits of applicability.



By the way, speaking of mathematics, even the structure we have is interesting. Mathematical analysis was designed to work in simple continuous space (manifolds that are close to Euclidean space). But what we have is different: within an infinitely large hypergraph we have something very similar to continuous space, but ordinary calculus is inapplicable (at least because our hypergraph may have a non-integer indicator of the number of dimensions). So we need to invent some generalization of calculus, which, for example, can deal with the curvature of non-whole-dimensional space. Probably the closest area of ​​modern mathematics to this problem is geometric group theory.



By the way, it should be noted that there are many subtleties in finding a compromise between changing the dimension of space and the presence of curvature in it. And despite the fact that it seems to us that we live in a three-dimensional universe, local deviations are quite possible, and most likely there were huge deviations in the early universe.

Time

In our models, space is defined by the structure of a hypergraph displaying a set of abstract relationships. But what is time?



In the last century, fundamental physics adopted the point of view that time is "like space", and that we should combine time and space into one entity and talk about the space-time continuum. And the theory of relativity points in this direction. But if there was one "wrong turn" in the history of physics in the last century, I think it was the assumption that time and space are related in nature. And despite the fact that in our models this is not the case, as we will see, relativity is perfectly deduced from them.



So what is time then? In fact, it is exactly as we feel it: the inexorable process of the course of events and their influence on the consequences. But in our models it is something much more precise: it is the consistent application of rules that constantly change the abstract structure that defines the contents of the universe.



The time model in our models is, in a sense, very computational. As time goes on, we actually see the results of more and more steps in the calculation. Indeed, the phenomenon of computational irreducibility implies that something definite and irreducible is “achieved” by this process. (And, for example, irreducibility is what I believe to be responsible for "encrypting" the initial conditions and related to the law of increasing entropy and the thermodynamic arrow of time.) It goes without saying that modern computer science did not exist a hundred years ago, when "space -time ", but the history of physics could be completely different.



In our models, time is simply the sequential application of rules. But there is a subtlety in how it works, which at first glance may seem like a trifle, but in fact it turns out to be the key to both the theory of relativity and quantum mechanics.



At the beginning of this article, I talked about the rule:

{{x, y}, {x, z}} → {{x, z}, {x, w}, {y, w}, {z, w}}



and showed the first few steps of applying this rule:





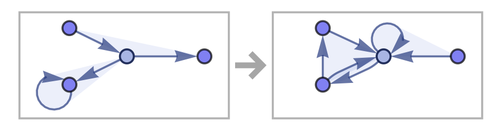
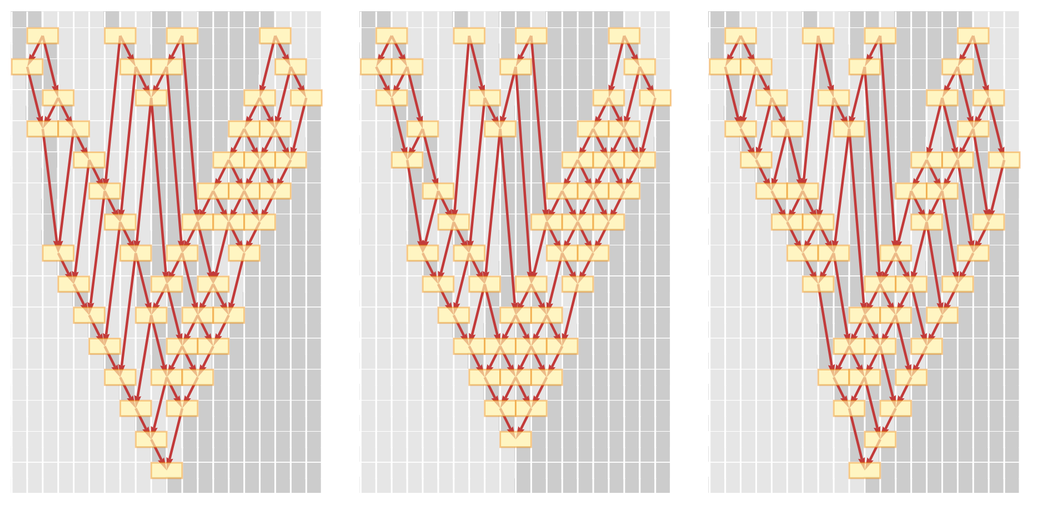
But how exactly was the rule applied? What is “inside” these steps? The rule defines how to take two edges in a hypergraph (which in this case is actually just a graph) and transform them into four new edges, thereby creating a new element. Thus, each "step" we showed earlier actually consists of several separate "update events" (here new added connections are highlighted, and those that are about to be deleted are marked with a dotted line):





This is not the only sequence of update events corresponding to rule. The rule simply says to find two adjacent connections, and if there are multiple possible options, it says nothing about which one is "correct." And the main idea in our model is to simply implement them all.



We can think of this as a graph showing all possible paths:





There are two possibilities for the very first update. Then, for each of these results, there are four additional possibilities. But on the next update, something interesting happens: the two branches are merged. In other words, even if we performed different update sequences, the result is the same.



Things get complicated quickly. Here's the graph after another update:





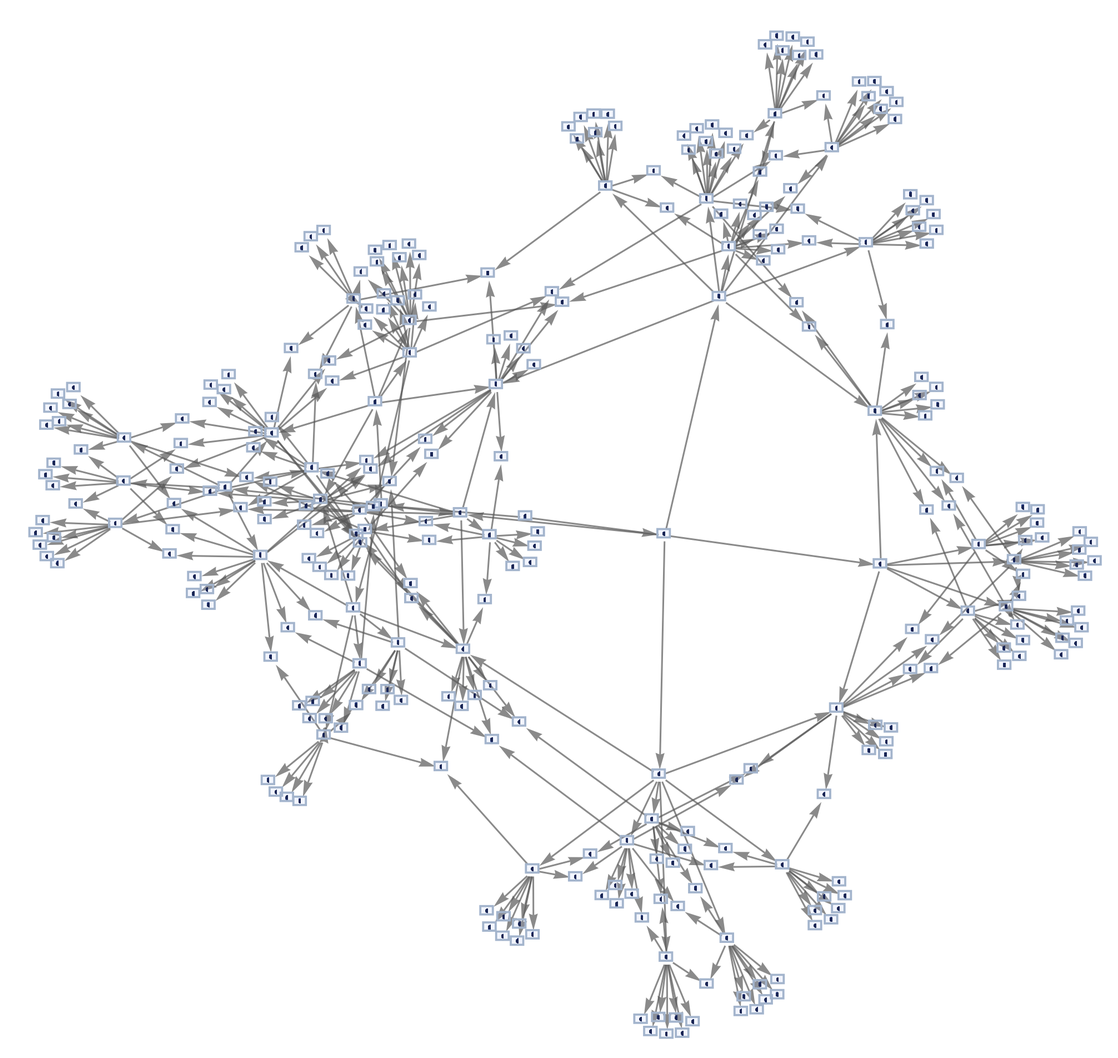
So how does this relate to time? It says that in the basic statement of the model there is not only one path of time, there are many paths and many "stories." But the model - and the rule used - defines them all. And we saw a hint of something else: even if we may think that we are following an "independent" path of history, it may actually merge with another path.



More research and discussion will be required to explain how this all works. But for now, let me say that it turns out that time is a causal relationship between events, and that in fact, even when historical paths are different, these causal relationships can be the same. And in fact, for the observer built into the system, there is only one stream of time.

Causal graph

In the end, everything looks wonderfully elegant. But to get to the point where we can understand the whole big picture, we need to take a closer look at some aspects. (Unsurprisingly, the fundamental theory of physics - inevitably built on very abstract ideas - is somewhat difficult to explain, but it couldn't be otherwise.)



To keep things simple, I won't talk directly about the rules that apply to hypergraphs. Instead, I'm going to talk about the rules that work with character strings.



Let's say we have a rule:

{A → BBB, BB → A}



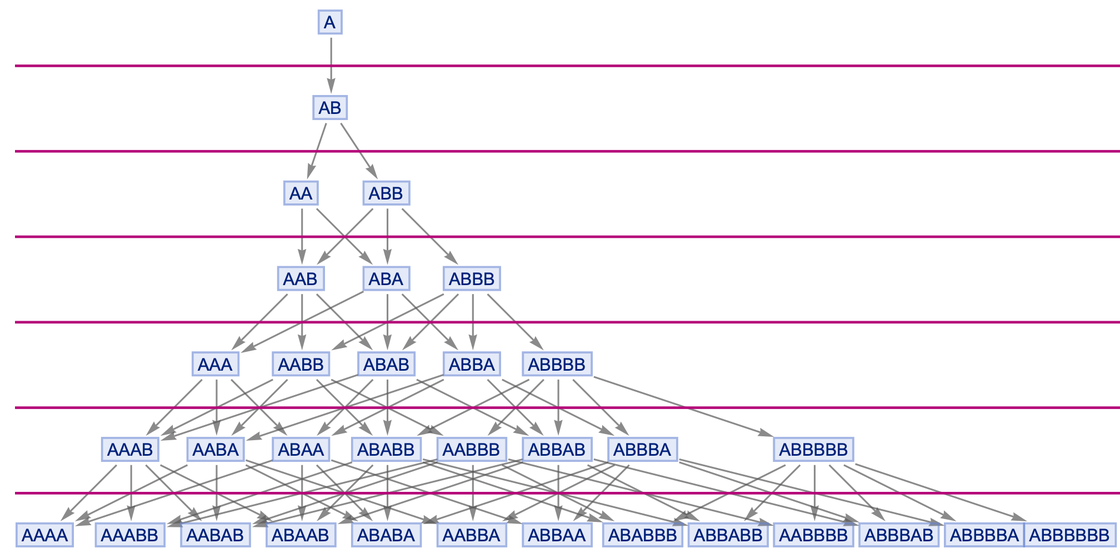
This rule says that wherever we see A we can replace it with BBB, and wherever we see BB we can replace it with A. So now we can generate what we call a branching system for this rule , and draw a "branch graph" that displays everything that can happen:





In the first step, the only option is to use A → BBB to replace A with BBB. But then there are two possibilities: replace either the first BB or the second BB - and these options give different results. However, in the next step, all that can be done is to replace the letter A - in both cases, getting BBBB.



In other words, although in a sense we had two historical paths that diverged in the branching system, it only took one step for them to merge again. And if you follow the picture above, you will find that it always happens with this rule: every pair of branches created is always merged, in this case after one more step.



This balance between branching and merging is what I call causal invariance. And although in this case it may seem like a trifle, in fact it turns out that this property of our models explains why the theory of relativity works, why there is objective reality in quantum mechanics, and many other basic questions of fundamental physics.



Let's explain why I call this property causal invariance. The picture above shows which "state" (that is, which line) leads to which other. But at the risk of complicating the picture (and note that this is incredibly simple compared to the case of a full hypergraph), we can annotate the multipath graph to include update events that lead to each state transition:





Now we can ask the question: what are the causal investigative links between these events? In other words, what event must happen before any other event can happen? Or, in other words, what events had to happen to create the input required for some other event?



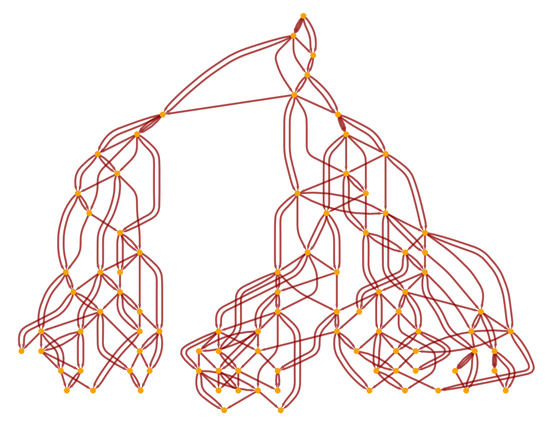
Let's go even further and annotate the graph above, showing all the causal relationships between events: The





orange lines show which event should happen before which other event - or what are all the causal relationships in the branching system. And yes, it looks complicated. But note that this picture shows the entire branching system with all possible historical paths, as well as the entire network of cause-and-effect relationships within and between these paths.



But the most important thing about causal invariance is that it implies that, in fact, the graph of causality is the same, no matter which historical path you take. And that's why I originally called this property causal invariance - because it says that with this rule, the causal properties are invariant with respect to the different variants of the sequence in which the update is performed.



And if you take another look at the figure above (and go through a few more steps), you can find that for each historical path, the cause-and-effect graph showing the cause-and-effect relationships between events will always look like:



or, we can draw it along to another:

The importance of causal invariance

To better understand causal invariance, it is useful to consider an even simpler example: the case of the BA → AB rule. This rule says that whenever there is a B followed by an A on a string, swap those characters. In other words, this rule tries to sort the string alphabetically, two characters at a time.



Let's say we start with BBBAAA. And here is a branch graph showing everything that can happen according to this rule:





There are many different paths you can take, depending on which BA in the line the rule applies to at each step. But what is important is that we see that in the end all the paths merge, and we get the only end result: a sorted string AAABBB. And the fact that we get this single end result is a consequence of the causal invariance of the rule. In such a case, when there is an end result (and not just constant development), cause-and-effect invariance says: it doesn't matter in what order you perform all the updates, the result you get will always be the same.



I introduced causal invariance in the context of trying to find a model of fundamental physics - and realized that it would be crucial for both the theory of relativity and quantum mechanics. But in fact, what amounts to causal invariance has been seen before in various forms of mathematics, mathematical logic, and computer science. (Its most common name is "associativity," although there are some technical differences between this and what I call causal invariance.)



Think of expanding an algebraic expression, for example (x + (1 + x)^2)(x + 2)^2. It doesn't matter in which order you follow the steps, you will always get the same result (in this case4 + 16x + 17x^2 + 7x^3 + x^4). And this independence of orders is in fact a cause-and-effect invariance.



One more example. Imagine you have a recursive definition, say: f[n_]:=f[n-1]+f[n-2](c f[0]=f[1]=1). Now let's try to calculate f[10]. You will receive first f[9]+f[8]. What will you calculate then: f[9]or f[8]? It does not matter. The result will always be 55. And this is another example of cause and effect invariance.



Those who have experience with parallel or asynchronous algorithms know that it is very important whether this algorithm has cause-and-effect invariance. Because it means that you can do something in any order - say, depth, breadth, or whatever - and you always get the same answer. The same thing happens in our little sorting algorithm above.



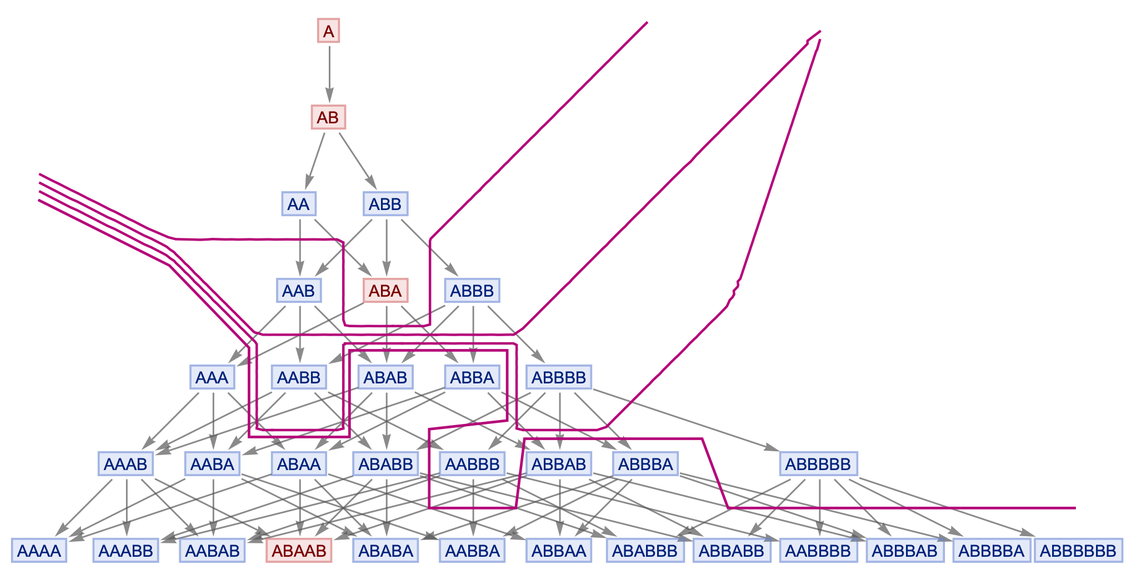
Okay, but now let's get back to causation. Here is the branching system for the sorting process, with annotations of all cause and effect relationships for all paths:





It's a mess. But since there is causal invariance, we know something very important: it's just a lot of copies of the same causal graph - a simple grid:





Incidentally - as you can see from the figure - the cross-links between these copies are non-trivial, and we will see later that they are related to the deep relationship between the theory of relativity and quantum mechanics, which is probably manifested in black hole physics. But we'll come back to this later ...



It is assumed that every other way of applying the sorting rule produces the same causal graph. So, here's one example of how we can apply a rule, starting from a specific starting line:





Now, let's show a graph of causation. And we can see that it's just a grid:





Here are three more possible update sequences:





We now see causal invariance at work: although different updates occur at different times, the graph of causal relationships between update events is always the same. And having seen this - in the context of a very simple example - we are ready to talk about the special theory of relativity.

Conclusion of the special theory of relativity

As a rule, doing science, you imagine how to conduct an experiment on a system, but you - as an "observer" - are outside the system. Of course, if you are thinking about modeling the entire universe and everything that exists in it, this is not a very smart way to think about the system. Because the observer is inevitably part of the universe, and therefore needs to be modeled like everything else.



In our models, this means that the "observer mind", like everything else in the Universe, must be updated through a series of events. There is no absolute way for the observer to know what is happening in the universe. All they have ever experienced is a series of renewal events that can be influenced by renewal events taking place elsewhere in the universe. Or, to put it another way, all that an observer can ever observe is a network of causal relationships between events - or the causal graph that we talked about.



As a toy model, let's look at our BA → AB rule for strings. You can imagine that the line lies in space. But the only thing our observer sees is a cause-and-effect graph, which represents the cause-and-effect relationships between events. And for the BA → AB system, this can be done as follows:





But now let's think about how observers can “sense” this causal graph. The observer itself is updated through some sequence of events. But even though this is “really what is happening,” in order to understand this, we can imagine that our observers create internal “mental” models of what they see. And for observers like us, it's natural enough to simply say, "One set of events happens throughout the universe, then another, and so on." And we can translate that into human by saying that we represent a series of "moments" in time where things happen "simultaneously" throughout the universe - with at least some conventions to define what we mean by simultaneous. (And yes, these ideas are similar to those of Einstein at the time,when he created special relativity.)



Here's a possible way to do it:





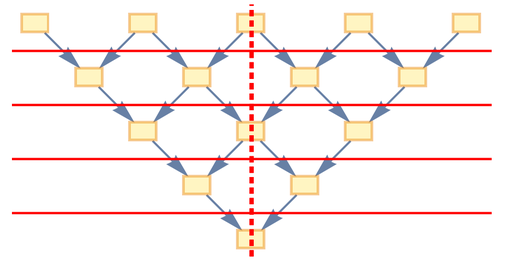
This can be described as "foliation" of the cause-effect graph. We cut the causal graph into slices. And our observers can regard each slice as a "sequential moment in time."



It is important to note that there are some restrictions on the choice of foliation. The causal graph determines what event should happen before what. And if our observers have a chance to make sense of the world, it's best if their view of the passage of time is consistent with what the causal graph says. So, for example, this foliation won't work - because it says that the timing we assign to events is inconsistent with the order in which they should happen:





What is the actual order of updating events implied by the above foliation? Basically, as many events as possible should happen simultaneously (that is, in the same slice of the foliation), like in this picture:





Now, let's link this to physics. The foliation that we had above refers to observers who are somehow "immobile in relation to the Universe" ("cosmological rest system"). One can imagine that over time, the events experienced by a particular observer are placed in a column going vertically down the graph:





But now let's think of an observer who moves uniformly in space. They will have a different sequence of events, like this:





This means that the foliation they build in a natural way will be different. From the outside, we can draw it on the causal graph as follows:





But for the observer, each slice represents a sequential moment in time. And they have no way of knowing how the causal graph was drawn. Thus, they will build their own version with horizontal slices:





Now we see a purely geometric fact: in order to perform this permutation, while maintaining the basic structure (and here and the corners) of the causal graph, each time there are fewer events in the causal graph to select c coefficient sqrt(1 - β^2), where β is the angle that represents the observer's speed.



If you understand something about special relativity, then you will learn a lot from it. What we call foliation corresponds to the "frames of reference" of the theory of relativity. And our foliations representing motion are the standard inertial frames of special relativity.



There is a particularly interesting point here: we can interpret this whole discussion of foliations and frames of reference in terms of the actual rules of evolution of our base frame. So, here is the evolution of our line sorting system in the inertial frame of reference, corresponding to an observer moving at a certain speed:





Because of the cause and effect invariance, it doesn't matter that we are in a different frame of reference - the cause and effect graph for the system (and the way it ultimately sorts the string) is exactly the same.



The main idea of ​​the special theory of relativity is that the laws of physics work the same in all inertial reference frames. But why should this be true? Well, our systems have an answer: it's a consequence of the causal invariance of the ground rules. In other words, we can deduce relativity from the property of causal invariance.



Usually in physics, relativity is introduced by establishing the mathematical structure of space-time. But in our models we do nothing of the kind, and in fact, space and time are not the same thing at all. We now see that, due to causal invariance, relativity appears in our models with all the connections between space and time that it implies.



So, for example, if we look at the image of our row sorting system above, we see relativistic time dilation. In fact, due to the foliation we have chosen, time flows more slowly. Or in other words, in an effort to speed up the sampling of space, our observer experiences a slower system update over time.



Light speed cin our toy system is determined by the maximum speed at which information can propagate, which is determined by the rule, and in the case of this rule, one symbol per step. Thus, we can say that our foliation corresponds to a speed equal to 0.3 of the speed of light. But now we can look at the formula for time dilation for our graph 1 / sqrt(1 - v^2/c^2), and this is exactly the formula that is said in the theory of relativity.



By the way, if we imagine that we are trying to make our observer move "faster than light", we will see that this does not work. Because in our picture there is no way to tilt the foliation more than 45 ° and still maintain the causal relationship.



So from our toy model, we can deduce the special theory of relativity. But here's the thing: this conclusion doesn't just work in the toy model - it applies to any rule that has causal invariance. Thus, even if we are dealing with hypergraphs, and not with strings, and there is a rule that has causal invariance, then (with various reservations, mainly about possible randomness in a causal graph) it will demonstrate relativistic invariance, and physics based on it will follow the special theory of relativity.

Energy and mass

In our model, everything in the Universe - space, matter, etc. - must be represented by the properties of our developing hypergraph. Does this hypergraph have mass and energy?



While this is a widely accepted concept in modern physics, I have never considered energy to be fundamental. It's just an attribute that objects (atoms, photons, whatever) can have. I have never thought of energy and mass as something that can be abstractly identified in the very structure of the universe.



So it came as a big surprise to me that our recent discovery that there is actually something in our model that we can point our fingers at and say "This is energy!" Technical Statement: Energy corresponds to the flow of causal ribs through spatial hypersurfaces. And by the way, the impulse corresponds to the flow of cause-and-effect edges through the temporary hypersurfaces.



What does this all mean? First, what is a spatial hypersurface? This is a standard concept in general relativity, which has a direct analogy in our models. This is what forms the slice in our foliation. We can distinguish two types of directions: spatial and temporal.



Spatial direction involves simple movement in space, and this is the direction in which you can always turn back and return. A temporal direction is a direction that also implies movement in time, where one cannot return. We can mark spatial hypersurfaces with a solid line, and temporal ones with a discontinuous line in the causal graph of our toy model:





(They can be called "surfaces", although "surfaces" are usually considered 2-dimensional, and our 3-dimensional + 1-dimensional universe, these layers of foliation are 3-dimensional: hence the term "hypersurfaces.")



Now let's take another look at the picture. “Causal edges are the causal relationships between events, shown in the figure as lines connecting events. Therefore, when we talk about the flow of causal edges through spatial hypersurfaces, we are talking about the number of edges that pass through horizontal slices in images.



It's easy to see this in a toy model. But here is a much more complex causal graph from another fairly simple model:





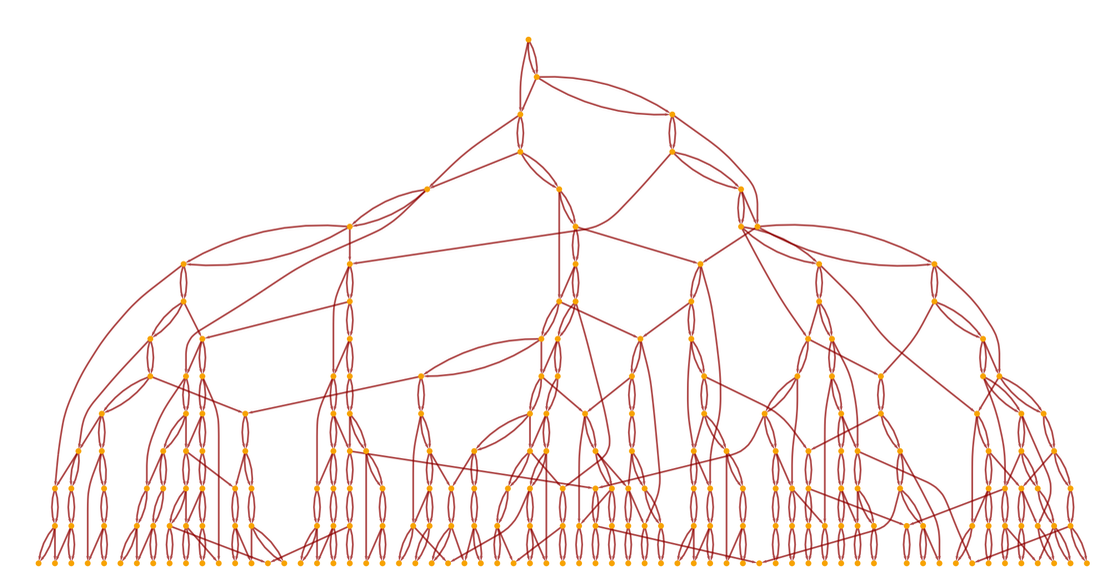
If we draw a foliation on this graph (thereby defining our frame of reference), we can start counting the number of causal edges going down through successive spatial slices:





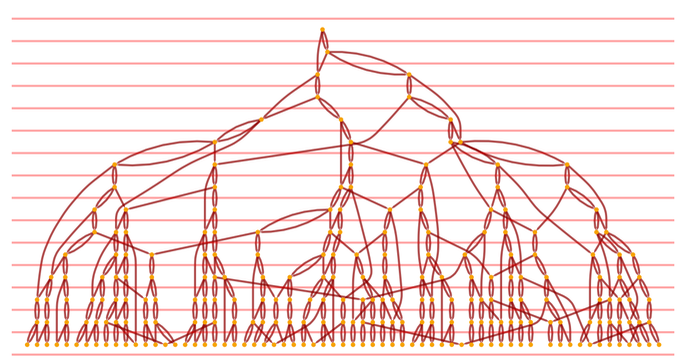
We can also look at how many causal ribs pass "sideways" through temporary hypersurfaces:





Why do we think these rib flows correspond to energy and momentum? Imagine what happens if we change the foliation, say, tilt it to match the motion at some speed, as we did in the previous section. We find out that our streams of cause and effect edges relate to speed in the same way as distance and time in the previous section.



Relativistic mechanics says that energy should correlate with velocity in the same way as time with velocity, and momentum with distance. We now know the reason. This is a fundamental consequence of our entire system and cause and effect invariance. In traditional physics, it is often said that position in space is a variable coupled to momentum, and energy is coupled to time. And this is specified in the mathematical structure of the theory. But here we are not just stating it as an axiom. This consequence follows naturally from our model.



This means that we can learn much more. For example, we may wonder what “zero energy” is. After all, if we look at one of our causal graphs, many of the causal edges actually just go to "maintain the structure of space." So, if in some sense the space is homogeneous, a homogeneous “background flow” of cause-and-effect edges is inevitably associated with it. And what we consider to be energy corresponds to the fluctuations of this flux around its background value.



By the way, it is worth mentioning what the flow of cause and effect edges corresponds to. Each causal edge is a link between events, which is "carried" by some element in the spatial hypergraph. Thus, the flow of causal edges is, in fact, the transfer of activity (that is, events) either in time (that is, through spatial hypersurfaces) or in space (that is, through temporal hypersurfaces). And we can say that energy is associated with activity in the hypergraph, which propagates information in time, while impulse is associated with activity that propagates information in space.



There is one fundamental feature of our causal graphs that we have not yet mentioned, and that is the dissemination of information. Start at any point (any event) in the causal graph. Then trace the causal relationship of this event. You will end up with something like a cone (here only in 2D):





It corresponds to such a concept of physics as a light cone . Suppose we have drawn our graph so that events are somehow located in space, then the light cone will show how information (transmitted by light) can propagate in space over time.



As the causal graph becomes more complex, the light cones become more complex. We will discuss the connection of this phenomenon with black holes later. For now, we can simply say that there are cones in our causal graph, and, in fact, the angle of these cones represents the maximum speed of information propagation in the system, which we can identify with the physical speed of light.



In fact, not only can we see light cones in our causal graph: in a sense, we can think of our entire causal graph as a large number of “elementary light cones” tied together. And, as we have already mentioned, most of the constructed structure is necessarily used to “maintain the structure of space”.



But let's take a closer look at our light cones. There are causal edges on their boundaries that do correspond to propagation at the speed of light — and which, from the perspective of the underlying hypergraph, correspond to events that “reach” and “capture” new elements as quickly as possible. But what about vertical causal ribs? These edges are associated with events that, in a sense, reuse elements in the hypergraph without involving new ones.



And it seems that these causal ribs have an important interpretation: they are associated with mass (or, more accurately, rest mass). So, the total flow of causal edges through spatial hypersurfaces corresponds to energy. And the flow of cause-and-effect relationships in the temporal direction corresponds to the rest mass. We can see what happens if we tilt our frame of reference a little, which corresponds to speed. v ≪ cIt is fairly easy to derive formulas for momentum (p) and energy (E). The speed of light c is included in the formulas because it determines the ratio of "horizontal" (that is, spatial) to "vertical" (that is, time) lines on the causal graph. And for v small enough in comparison with c we get:



p = mv + ...

E = mc^2 + 1/2 m\*v^2 + ...



So, from these formulas, we can see that by simply examining causal graphs (and, yes, given causal invariance and a whole host of detailed mathematical constraints that we are not discussing here), we were able to derive the basic (and well-known) fact about the ratio of energy and mass:



E = mc^2



In standard theories of physics, this ratio looks more like an axiom than something that can be deduced. But this is not the case in our model.

General relativity and gravity

Earlier we talked about how space curvature occurs in our models. But then we were just talking about "empty space". Now we can go back and talk about how curvature interacts with mass and energy in space.



Above, we talked about constructing spherical balls, starting from some point of the hypergraph, and then following all possible sequences of r edges. But now we can do something directly similar in the graph of cause and effect: start from a certain point and trace the possible sequences of t connections. We get "volumes of light cones".



If the space is d-dimensional, then this volume will approximately grow ast^(d+1)... But, as in the case of space, there is a correction term, this time proportional to the so-called Ricci tensor Ruv. (The actual expression is roughly t^(d+1)\*(1 - 1/6t(i)t(j)R(ij))where t (i) corresponds to time vectors, etc.)



We also know a little more about what is inside the light cones: there are not only 'background connections' that support the structure of space, but also' additional "cause-and-effect relationships associated with energy, momentum and mass. And we can identify their density with the so-called energy-momentum tensor T (uv). Thus, we end up with two contributions to the "volumes" of our light cones: one from "pure curvature" and one from energy-momentum.



Again, we need a little math here.... But the main thing is to think about the limit when we look at a very large causal graph. Which equation must be true to have d-dimensional space, rather than something more unusual? The following equation must be fulfilled:



R(uv) - 1/2 Rg(uv) = sigma T(uv)



This is exactly the Einstein equation for the curvature of space, in which matter with a certain energy and momentum is present. We are missing out on many details here. But still, in my opinion, this is quite impressive: based on the basic structure of our very simple models, we can get a fundamental result: an equation that has passed all the tests in describing gravity for over a hundred years.



I would like to emphasize that in the equation just given there is no so-called cosmological term. And this is connected with the question of what is zero energy and which properties of the hypergraph are directly related to the "maintenance of space", and which - to matter in this space.



In modern physics, it is expected that even in a vacuum there actually exists a formally infinite density of pairs of virtual particles. In fact, pairs of particles and antiparticles are constantly being born, which quickly annihilate, but which together create a huge energy density. We will discuss how this relates to quantum mechanics later. But for now, just recall that particles (for example, electrons) in our models correspond to local stable structures in the hypergraph.



How is space "maintained"? Basically, this happens through all sorts of seemingly random update events in the hypergraph. But in modern physics (or in particular in quantum field theory) we have to describe everything in terms of (virtual) particles. So if we try to do this with all these random update events, it's no surprise that we end up saying there are an infinite number of events going on. (Yes, it can be done much more accurately; I'm just giving a general outline here.)



But then the immediate problem arises: we say that there is a formally infinite - or at least enormous - energy density that must exist throughout the universe. If we then look at Einstein's equation, we conclude that such density must produce enough curvature to fold the universe into a tiny ball.



One way to find a way out of this paradox is to introduce the so-called cosmological term, and then postulate that this term has such a value that it could be taken for zero energy density from virtual particles. This is definitely not the best solution.



Everything is different in our models. What in our model corresponds to virtual particles actually "creates space" and maintains its structure. Of course, all the details depend on a particular ground rule. But there is no longer a big mystery as to why "vacuum energy" basically does not destroy our universe - this is because it creates our universe.

Black holes and the singularity

One of the main predictions of general relativity is the existence of black holes. Do they exist in our models? Of course! The defining feature of a black hole is the presence of an event horizon: a boundary that light signals cannot cross, and where causation is actually broken.



In our models, we can see how this happens in the causal graph. Here's an example:





In the beginning, everything is causally connected. But at some point, the causal graph splits and an event horizon appears. Events occurring in one part of the graph cannot affect others. This is how a region of the universe can "causally break away" to form something like a black hole.



But in fact, in our models, the "gap" can be even more extreme. Not only a causal graph can split - a spatial hypergraph can discard separate parts, each of which, in fact, forms a whole "separate universe":





By the way, it is interesting to see what happens to the layers that observers see when the event horizon exists. Causal invariance says that diverging paths in a causal graph must always merge over time. But if the paths go to different unconnected parts of the causal graph, this will never happen. How does this affect observers? Well, basically, they have to "stop time." They must have a lamination in which successive time slices simply accumulate and never enter the disconnected parts.



This is similar to what happens in general relativity. To an observer far from the black hole, it will seem that it takes an infinite time for something to fall into it. So far, this is just a phenomenon associated with the structure of space. But we will see later that it is also a direct analogue of something completely different: the measurement process in quantum mechanics.



Coming back to gravity: we can ask questions not only about the event horizon, but also about singularities in space-time. In our models, these are the places where many paths in the causal graph converge at one point. In our models, we can immediately examine questions such as whether the event horizon is always associated with a singularity ("the cosmic censorship hypothesis").



We can think of other strange phenomena from general relativity. For example, there are closed time curves that are sometimes seen as allowing time travel. In our models, closed time curves are incompatible with causal invariance. But we can of course invent the rules that generate them. Here's an example:





In this branching system, we start with one "initial" state. But as we move forward, we may enter a cycle in which we visit the same state repeatedly. And this cycle is also visible in the cause and effect graph. We think we are "going forward in time." But in reality, we are just looping, repeatedly returning to the same state. And if we tried to find a foliation in which we could describe time as always going, we simply could not do it.

Cosmology

In our model, the universe could start with a tiny hypergraph - perhaps with a single loop. But then - as the transformation rule is applied - it gradually expands. Under some particularly simple rules, the overall size of a hypergraph should simply increase uniformly; under others, it can fluctuate.



But even if the size of the hypergraph is constantly increasing, we may not notice it. It can happen that practically everything we see also expands - so in reality the granularity of space is getting thinner and thinner. This would be an interesting resolution to the age-old debate over whether the universe is discrete or continuous. Yes, it is structurally discrete, but the scale of discreteness in relation to our scale is constantly getting smaller and smaller. And if it happens fast enough, we can never "see discreteness" because every time we try to measure it, the universe actually splits up before we even get a result. (This would somehow be like the ultimate proof of the epsilon-delta calculus: you are challenging the universe with the epsilon delta.and before you can get a result, the universe shrinks the delta.)



There are other possibilities as well. The entire hypergraph of the Universe can be constantly expanding, but the pieces are constantly “breaking off”, forming black holes of different sizes and allowing the “main component” of the Universe to change in size.



But regardless of how such expansion works in our Universe today, it is clear that if the Universe started with a single loop, it would have to expand strongly, at least initially. And there is an interesting possibility here that has to do with understanding cosmology.



Our present universe is three-dimensional space, but there is no reason in our models that the early universe was necessarily the same. All kinds of things can happen in our models:





In the first example, different parts of the space are divided into non-communicating branches. In the second example, we have something like an ordinary two-dimensional space. And in the third example, space is in a sense very strongly connected. If you calculate the volume of a spherical ball, it will not grow like r^d, it will grow exponentially with increasing r (for example, how 2^r).



If we look at the causal graph, we can see that you can “travel all over the place in space” or very quickly influence every event. As if the speed of light is infinite. But in reality, this is because space is actually infinite-dimensional.



In modern cosmology, there is an acute question of how different parts of the early Universe managed to "communicate" with each other in order to smooth out disturbances. The answer becomes obvious if we assume that the Universe was actually infinite-dimensional at the beginning and only later "relaxed" to a finite-dimensional one.



What in the universe today is a reflection of events that occurred at the earliest stage of its history? The fact that our models are fairly chaotic means that most of the characteristics of the initial conditions or very early stages of the Universe will be quickly “encrypted” and cannot be reconstructed.



But it's entirely possible that something like the symmetry breaking associated with the first few hypergraphs might somehow survive. And this suggests the possibility that something like the angular structure of the cosmic microwave background or a very large-scale distribution of galaxies could reflect the discrete structure of the very early universe. Or, in other words, it is quite possible that the basic rule of our universe is drawn across the sky. I consider this possibility extremely unlikely, but it would certainly be great if the universe "self-documents" in this way.

Elementary particles - old and new

We have spoken several times about particles such as electrons. In modern physical theories, it is assumed that various truly elementary particles - quarks, leptons (electron, muon, neutrino, etc.), gauge bosons, Higgs bosons - are essentially point-like particles of zero size. This is not how it works in our models. In essence, particles are “little pieces of space” with various special properties.



I am guessing that the exact list of existing particles depends on the specific basic transformation rule. In cellular automata, for example, we can see complex sets of possible localized structures emerge:





In our hypergraphs, the picture will inevitably be somewhat different. The main property of each particle will be some locally stable structure in a hypergraph (a simple analogy is a piece of "nonplanarity" in a planar graph). And then a lot of cause-and-effect edges will be associated with the particle, determining its specific energy and momentum.



However, the basic characteristic of particles will presumably determine things like their charge, quantum numbers, and possibly spin - and the fact that these things are observed in discrete units may reflect the fact that only a small chunk the hypergraph is involved in their definition.



It is rather difficult to understand what is the real scale of space discreteness in our models. But a possible (albeit potentially unreliable) estimate is such that the "elementary length" is about10^–93meters. (Note that this is very small compared to the Planck length of ~ 10^–35meters, which is essentially the result of a dimensional analysis.) And with this elementary length, the radius of an electron could be 10^–81meters. Tiny, but not null. (Note that current experiments only tell us that the size of an electron is less than 10^–22meters.)



Also, our models assume the existence of a "mass quantum" - a discrete quantity of which all masses, such as particles, are multiples. In our estimate of the elementary length, this quantum of mass would be small, perhaps, in 10^–30, or in 10^36times less than the mass of an electron.



And here an intriguing hypothesis arises. Perhaps particles such as electrons that we currently know about are "big". (We estimate that there should be hypergraph elements in the electron.) And there are possibly much smaller and much lighter particles. Compared to the particles we currently know, there would be few hypergraph elements in such particles, so I call them "oligons" (from the Greek word ὀλιγος, meaning "several").



What properties will these oligones have? They probably very, very weakly interact with other particles in the universe. Most likely, many oligons were produced in the very early universe, but due to their very weak interaction, they very soon "fell out of thermal equilibrium" and remained in large numbers in the form of relics - with energies that will gradually decrease as they grow.



So where are the oligons now? Even if their other interactions are likely to be extremely weak, they will still be subject to gravity. And if their energy turns out to be low enough, they will collect in gravitational wells throughout the universe, that is, in and around galaxies.



And this is especially interesting in light of the fact that there is now a great mystery about the amount of observed mass in galaxies. It seems that there is a lot of "dark matter" that we cannot see, but which has gravitational effects. Well, maybe they are oligons. Maybe even many different kinds of oligons: a whole world of shadows made of much lighter particles.

Quantum mechanics

"But how do you get quantum mechanics?" - physicists always asked me this when I described earlier versions of my models to them. In many ways, quantum mechanics is the pinnacle of existing physics. However, there was always a certain "you are not expected to understand this" in it, combined with "just believe the mathematical formulas." And yes, mathematical formulas allow us to make calculations. These calculations are often very complex - so complex that they made me start using computers for mathematical calculations 45 years ago.



Our usual impression of the world is that certain things happen. Prior to quantum mechanics, classical physics usually fixed this in laws - usually equations - that told exactly what the system would do. But quantum mechanics assumes that any given system does a lot of different things "in parallel", and we just observe the likely cases of these possibilities.



For a model that has certain rules, it can be assumed that it can never reproduce quantum mechanics. But in fact, in our models, quantum mechanics is not only possible, it is absolutely inevitable. And, as we will see later, it is amazingly beautiful that quantum mechanics is in its essence very close to the theory of relativity.



So how does it all work? Let's go back to what we discussed when we first talked about time. Our models have a specific rule for updates to be made to our hypergraphs, for example:





But if we have such a hypergraph:



there are usually many places where this rule can be applied. So which update should we apply first? The model doesn't tell us anything about it. But let's just imagine all the possibilities. The rule tells us what they all are - and we can think of them (as we discussed above) as a branching system - here this is illustrated using the simpler case of strings rather than hypergraphs:





Each node on this graph represents the complete state of our system (a hypergraph in our real world models). And each node is connected by arrows with state or states that can be obtained by applying one update to it.



If our model worked like classical physics, we would expect it to progress in time from one state to another, let's say:





But the structure of our models leaves us no choice but to consider branch systems. The form of the entire branching system is completely determined by the rules. But in a way that already closely resembles the standard mathematical apparatus of quantum mechanics, the branching system defines many different possible paths of history.



If there are always all these different possible paths of history, how do certain things happen in the world? This has been the main mystery of quantum mechanics for over a century. It turns out that if you just use quantum mechanics to compute, the answer doesn't really matter. But if anyone wants to truly understand what's going on in quantum mechanics, it definitely matters.



Most interestingly, our models have an obvious solution. It is based on the same phenomenon — causal invariance that is the cause of relativity.



Here's how it works... The key is to think that the observer, who is himself part of the branching system, will infer about the world. Yes, there are different possible paths of history. But - as in our discussion of the theory of relativity - the only aspect of them that an observer ever realizes is the cause-and-effect relationship between events. The point is that even if the paths look different from the outside, causal invariance implies that the network of relationships between events (which is all that matters when a person is inside the system) will always be exactly the same.



In other words, as in the case of relativity, even though many possible "threads of time" may appear from outside the system, from within the causal invariance of the system implies that ultimately there is only one thread of time, or, in fact, one objective reality.



How does all of this compare with the detailed standard mathematical apparatus of quantum mechanics? These are quite complex calculations, but let me make at least a few notes on this here. (There are some details in my whitepaper; Jonathan Gorard gave even more in his work.)



The states in the branching system can be considered as possible states of the quantum system. But how can we characterize how observers perceive them? In particular, what states does the observer know about and when? As with relativity, the observer can, in a sense, choose how they define time. One of the possibilities might be to stratify the branching system, for example:





In terms of quantum mechanics, we can say that each time the observer experiences a superposition of the possible states of the system. In direct analogy with the case of relativity, there are many different possible choices that an observer can make about how to determine time - and each of them corresponds to a different foliation of the graph.



Again, by analogy with the theory of relativity, we can view these options as different "frames of reference for quantum observation." Cause-and-effect invariance implies that as long as they respect the cause and effect relationships in the graph, these frames of reference can be customized the way we want. Speaking of relativity, it was useful to have simply "oblique parallel lines" ("inertial frames of reference") representing observers who move uniformly through space.



Other frames of reference can also be used when talking about quantum mechanics. In particular, in the standard terms of quantum mechanics, it is customary to speak of "quantum measurement": in essence, it is the act of taking a quantum system and determining from it a certain (essentially classical) result. Well, in our model, the quantum measurement basically corresponds to a specific quantum observation system.



Here's an example:





Consecutive pink lines represent what the observer considers consecutive points in time. So when all the lines are grouped below the ABBABB state, it means that the observer is actually "freezing time" for that state. In other words, the observer says, "I believe this is a state of the system, and I stick to it." Even though all kinds of other "quantum mechanical" evolution of states occur in the complete graph, the observer has tuned his quantum observation system so that he receives only a concrete, definite, classical state as a result.



Can observers do this constantly? Well, it depends on the structure of the graph, which depends on the underlying rule. In the example above, we have created a foliation (ie, a quantum observation system) that best fulfills this rule during "freeze time" for the ABBABB state. But how long can this “reality distortion field” be maintained?



The only way to maintain the integrity of the foliation in the above graph is to gradually expand it over time. In other words, in order for time to remain frozen, more and more quantum states must be drawn into the “reality distortion field,” and therefore there is less and less coherence in the system.



The picture above refers to a very trivial rule. Here is the corresponding image for a more realistic case:





And here we see that even in this still incredibly simplified case, the structure of the multilateral system will force the observer to construct more and more complex foliation if he wants to successfully freeze time. Measurement in quantum mechanics has always been accompanied by a somewhat awkward mathematical idealization - and now this gives us an idea of ​​what is really going on. (The situation is ultimately very similar to the problem of decoding "encrypted" thermodynamic initial conditions, which I mentioned above.)



The quantum dimension is what the observer perceives. But if you, for example, are trying to build a quantum computer, the question is not only that the qubit is perceived as being maintained in a certain state, it really needs to be kept in that state. And for this to happen, we need to stop time for this qubit. Here is a very simplified example of how this can happen in a branch graph:





All this talk of "freezing time" may seem strange and not like everything that is usually talked about in physics. But in fact, there is a connection: the freezing of time, which we are talking about here, can be considered as happening, because in the space of quantum branching we have an analogue of a black hole in physical space.



We have a place where things go and get stuck there forever. But that's not all. If you are an observer far from a black hole, you will never see anything fall into a black hole in a finite time (which is why black holes are sometimes called "frozen stars"). And the reason for this is precisely because (according to mathematics) time is frozen on the event horizon of a black hole. In other words, to successfully create a qubit, you must isolate it in quantum space in the same way that particles are isolated in physical space due to the event horizon of a black hole.

General relativity and quantum mechanics are the same essence!

General relativity and quantum mechanics are two of the great fundamental theories of modern physics. In the past, we often could not put them together. One of the great results of our project was the realization that, at some deep level, general relativity and quantum mechanics are actually the same idea. This is only clear in the context of our models. Both theories are consequences of cause-and-effect invariance, simply applied in different situations.



Think back to our discussion of causal graphs in the context of relativity. We drew foliations and said that if we look at a certain slice, it will tell us about the position of the system in space at what we consider to be a certain moment in time. So now let's take a look at branch graphs. In the previous section, we saw that in quantum mechanics we are interested in their foliations. But if we look at a specific slice of one of these foliations, what is it? There are several states in foliation. And it turns out that we can think of them as located in an abstract form of space, which we call "the space of ramifications."



To understand this space, we must have a way of saying what is next to what. The branch graph allows us to do this. Take a look:





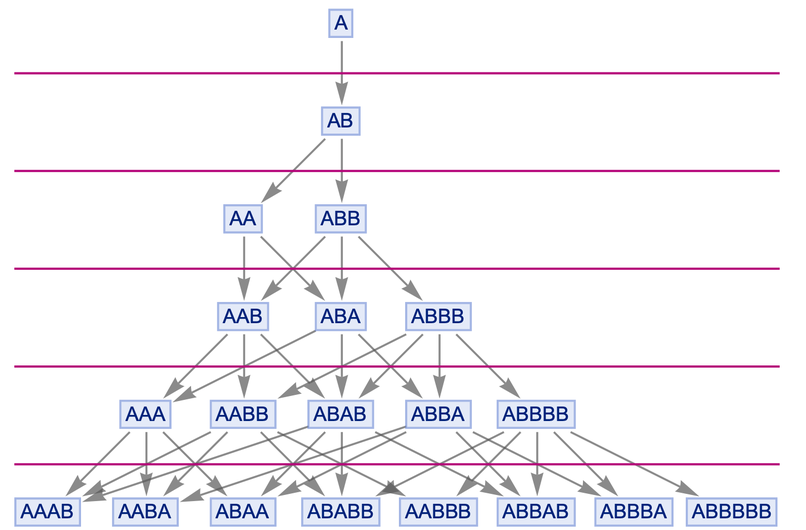
On each slice of the foliation, draw a graph in which we connect two states whenever they are both part of the same "branch pair", so that, like AA and ABB here, they both come from the same state on the slice ... Here's what we get when doing this for successive slices:





We call these graphs "branch graphs". We can think of them as correlations - or entanglements - of quantum states. Two adjacent states on the graph are highly entangled; those further away are smaller. And we can imagine that as our system evolves, we will get larger and larger branching graphs, until eventually, as in the case of our original hypergraphs, we can not think of these graphs as something like continuous space.



What does this space look like? For our original hypergraphs, we imagined that we would get something like ordinary physical space (say, close to three-dimensional Euclidean space). But branch space is something more abstract and much more unusual. And it is not even finite-dimensional. It's kind of like a Hilbert space. But we can still think of it mathematically as some kind of space.



At this point, things get very complicated. But let me try to give you at least an idea of ​​how things work. Here's an example of a wonderful correspondence: the curvature of physical space is like the uncertainty principle of quantum mechanics. Why are they somehow related to each other?



The Uncertainty Principle says that if you measure, say, the position of something and then its momentum, you will not get the same answer as if you did it in reverse. But now think about what happens when you try to create a rectangle in physical space, moving first in the x direction, then in the y direction, and then you do it in reverse. In flat space, you will be taken to the same place. But in curved space this is not the case:





Essentially, the uncertainty principle is that you do exactly this, but in the space of ramifications, not in the physical. And precisely because the branch space is unusual - and, in fact, very curved - you get the uncertainty principle.



Well, the following question may arise: what is the analogue of Einstein's equations in the branch space? And again, an amazing thing is revealed: this is the path integral - the fundamental mathematical construction of modern quantum mechanics and quantum field theory.



Let me try to explain. In the same way that we discussed geodesic lines as describing paths traversed through physical space over time, we can discuss geodesic lines as describing paths traversed through ramification space over time. In both cases, these geodesic lines are determined by the curvature in the corresponding space. In the case of physical space, we have argued that the presence of redundant causal edges corresponding to energy will result in what is equivalent to the curvature of the spatial hypergraph, as described by Einstein's equations.



What about branch space? As with the spatial hypergraph, we can think of the causal relationships between update events that define the branch graph. And we can again imagine the flow of cause-and-effect edges - now not through spatial hypersurfaces, but through hypersurfaces like branches of states - as corresponding energies. And - as in the case of the spatial hypergraph - the excess of these causal edges will lead to the fact that it will create a curvature in the space of ramifications (or, more precisely, in the "time-ramification" - an analogue of space-time). But this curvature will then affect the geodesic lines crossing the branch space.



In general relativity, the presence of mass (or energy) causes space to bend, causing the paths of the geodesic lines to rotate, which is usually interpreted as the action of gravity. There is an analogue in quantum mechanics in our branch space. The presence of energy causes a curvature in the branch space which causes the geodesic paths through the branch space to rotate.



What does the turn correspond to? In fact, this is exactly what the path integral says. The path integral (a standard term in quantum mechanics) is given in complex numbers. But you can just as well consider it as a turn by an angle. This is exactly what happens to our geodesic lines in the branch space. The path integral contains a quantity called action, which is a kind of relativistic analogue of energy. Our streams of causal edges correspond to action, and it is they that determine the speed of rotation of geodesic lines.



It all goes well together. In physical space, we have Einstein's equations - the core of general relativity. And in the space of ramifications, we have an integral over the Feynman trajectories - the core of modern quantum mechanics. And in the context of our models, they are just different facets of the same idea. This is an amazing combination that I did not expect at all. It arose as an inevitable consequence of our simple models of applying rules to relation sets or hypergraphs.

Branch movement and the horizon of entanglement

We can think of motion in physical space as a process of exploring new elements in a spatial hypergraph, potentially subject to their influence. But now, when we talk about the space of ramifications, it is reasonable to ask if there is something like motion in it. And the answer is yes. Instead of exploring new elements in the spatial hypergraph, we explore new elements in the branch graph and become potentially influenced by them.



There is a way to say this in the standard language of quantum mechanics: as we move through the branching space, we actually "get entangled" in more and more quantum states.



Let's continue the analogy. In physical space there is a maximum speed of movement - the speed of light c... So what about branch space? Well, in our models we see that there should also be a maximum speed of movement in the branch space. Or, in other words, there is a maximum speed at which we can communicate with new quantum states.



In physical space, we talk about light cones as regions that can be causally influenced by an event at a specific location in space. In the same way, we can talk about entanglement cones that define regions in the branch space that can be influenced by events at some position in the branch space. And just as there is a causal graph that ties together elementary light cones, there is something similar that ties together entanglement cones.



This is somewhat similar to a branching causal graph: a graph that represents the causal relationship between all events that can occur anywhere in the branching system. Here is an example of such a causal graph for just a few steps of a very simple string substitution system:





In a manner. a causal graph is the most comprehensive description of anything that can affect the experience of observers. Some of the causal relationships described are spatial relationships; some are branched links. But they are all there. So, in a sense, a branching causal graph is where relativity and quantum mechanics meet. Cut to one side and you see relationships in physical space; take a shortcut and you will see the branch space relationships between quantum states.



To understand how this works, here's a toy version of a causal branch graph:





Each point is an event that occurs in some hypergraph on some branch of the system. And now the graph shows the causal relationship of this event with others. In this toy example, there is a purely temporary relationship (indicated by down arrows), in which basically some element of the hypergraph influences his future self. But there are both spatial and branching relationships when an event affects elements that are either "spatially" separated in the hypergraph, or "branched" separated in the branching system.



But with all this complexity, something wonderful is happening. If the basic rule of the model has cause-and-effect invariance, then this implies all kinds of regularities in the cause-and-effect branching graph. For example, all those causal graphs that we get by taking different time-branching slices are actually the same when we project them into space-time - and this leads to the theory of relativity.



But causal invariance has other consequences as well. One of them is that there must be an analogue of the special theory of relativity, applicable not to space-time, but to time-branching. The frames of reference for special relativity are now our quantum observation systems. And the analogue of speed in physical space is the speed of entanglement of new quantum states.



So what about the phenomenon of relativistic time dilation? Is there an analogue of this for motion in branch space? Actually, yes, there is. And this turns out to be what is sometimes called the quantum Zeno effect: if you repeatedly measure a quantum system fast enough, it will not change. This phenomenon is implied by the additions to the standard apparatus of quantum mechanics that describe measurements. But in our models this comes directly from the analogy between physical space and branch space.



Making new measurements is equivalent to entangling in new quantum states or moving around in branch space. In direct analogy to what happens in special relativity, when you get close to moving at maximum speed, you inevitably slow down your sampling in time - and therefore you get time dilation, which means your "quantum evolution" is slowing down.



So, there are relativistic phenomena in physical space and quantum analogs in branching space. But in our models, these are essentially aspects of one thing: the causal branch graph. So are there situations in which two types of phenomena can mix? Usually not: relativistic phenomena cover large physical scales; quantum phenomena tend to involve small ones.



But one example of an extreme situation where they can mix is ​​black holes. I have mentioned several times that the formation of the event horizon around a black hole is associated with a break in the cause-effect graph. But that's not all. In fact, this separation exists not only in the causal space-time graph, but also in the complete causal ramification graph. This means that there is not only the usual causal horizon of events - in physical space - but also a "horizon of entanglement" in the space of ramifications. And just as part of a spatial hypergraph can "fall off" in a black hole, so can part of a branch graph detach.



What does it mean? There are many consequences. One is that quantum information can be trapped within the entanglement horizon, even if it has not crossed the causal event horizon - so in reality the black hole freezes quantum information “on its surface” (at least on its surface in the space of ramifications). This is a strange phenomenon implied by our models, but perhaps what is particularly interesting about it is that it is in many ways consistent with the conclusions about black holes made in some of the latest work in physics on the so-called holographic principle in quantum field theory and general theory relativity.



Here is another related phenomenon. If you cross the causal horizon of a black hole, you will end up physically lengthening infinitely (or "spaghettized") by tidal forces. Well, something similar happens if you cross the horizon of confusion, but now you will be elongated in the space of ramifications, not in the physical. And in our models, this ultimately means that you cannot make a quantum measurement - so in a sense, as an observer, you cannot “form a classical picture of the world,” or, in other words, go beyond entanglement. On the horizon, you can never “come to a final conclusion,” such as whether something fell into a black hole or not.



Light speed c- a fundamental physical constant that connects distance in physical space with time. A new fundamental physical constant has appeared in our models: the maximum cohesion speed, which links the distance in the space of branches with time. I call this maximum speed of entanglement ζ (zeta) ( ζ is a bit like "entangled c "). I'm not sure what its exact meaning is, but in my estimate it corresponds to the entanglement of about 10^102new quantum states per second. And in a sense, the very fact that it is so large allows us to "form a classical picture of the world."



Because of the relationship between branched causal edges and energy, it is possible to convert ζ to units of energy per second, and our estimate assumes that ζ is about 10^5solar masses per second. It's a big deal - it probably has something to do with galactic black hole mergers. (This would mean that it would take perhaps six months for the mind to be able to "quantum grasp" our galaxy.)

Finding the primary rule

I am sincerely amazed at how much we were able to figure out just from the general structure of our models. But to get a definitive fundamental theory of physics, we still need to find a specific rule. A rule that gives us 3 (or so) dimensions of space, a specific expansion rate of the Universe, specific masses and properties of elementary particles, and so on. But how do we start looking for this rule?



And in fact, even before that, we need to ask: if we had the right rule, would we understand it? As I mentioned earlier, this is potentially a big problem with computational irreducibility. Because, whatever the basic rule, our real Universe has applied it, perhaps more than 10^500once.



And if computational irreducibility exists (and it does), then there will be no way to drastically reduce the amount of computational effort required to determine the outcome of all these rule applications.



But we must hope that somehow - even though the overall evolution of the universe is not computable - there are still enough “tunnels of computational reducibility” for us to figure out the data we need to compare with what we know about physics without having to do all this computational work. And I must say that our recent success in drawing conclusions only from the general structure of our models gives me optimism about this possibility.



What rules should we consider? The traditional approach in natural science (at least for the last several centuries) has generally boiled down to this: start with what you know about any system you study, and then try to "reverse engineer" its rules. But there is too much empirical evidence in our models for this to work. Take a look at this:





Given the general shape of this structure, you would never have guessed that it could be created with a simple rule:

{{x, y, y}, {y, z, u}} → {{u, z, z}, {u, x, v}, {y, u, v}}





I have explored computational universes for about forty years, and I must say that even now, it is amazing how often I am amazed at the ability of extremely simple rules to induce behavior that I did not even expect. And this is especially true for the completely structureless models that we use. In the end, the only real way to know what might happen in these models is to simply list the possible rules and then run them and see what happens.



But now another question arises. If we start listing very simple rules, how far will we have to go before we find our universe? Or, in other words, how simple is the rule for our universe?



Perhaps, in a sense, the rule for the universe will have a special case for every element of the universe — every particle, every position in space, and so on. Scientific laws suggest that the rule does not have this level of complexity. But how simple will it be? We do not know. And I have to say that I don't think our recent discoveries shed any particular light on that - because they basically say that many things in physics are general and independent of the specifics of a basic rule, no matter how simple or complex. it was not.

Why this particular universe?

Well, okay, let's say we find that our universe can be described by some definite rule. Then the obvious next question arises: why is this a rule, and not some other? The history of science since Copernicus has shown us over and over again evidence that we are "not special." But if the rule that describes our Universe is simple, wouldn't this simplicity be a sign of a "singularity"?



I've been thinking about this for a long time. Could it be, for example, that the rule is simple only because of how we, as entities existing in our particular universe, choose our own ways of describing reality? And that in some other universe, with some other rule, the beings that exist there will establish their ways of describing reality so that the rule of their universe is simple for them, although it can be very difficult for us?



Or it could be that, in some fundamental sense, it doesn't matter what the rules for the universe are: for observers embedded in the universe, operating by the same rules as this universe, the inferences about how the universe works will always be the same ?



Or maybe this is a question outside the scope of science?



Much to my surprise, the paradigm that has emerged from our recent discoveries potentially seems to offer a definite - albeit seemingly strange - scientific answer.



In what we have discussed so far, we imagine that there is a special, unique rule for our universe that applies over and over again, effectively in every way possible. But what if there wasn't a single rule that could be used? What if every conceivable rule could be used? What if every update event could just use every possible rule? (Note that only a finite number of rules can apply in a finite universe.)



At first, it may seem that such a model will never lead to anything definite. But imagine building a branch graph of absolutely everything that can happen, including all events for all possible rules. This is a large complex object. But it is far from being structureless, it is full of all kinds of structures.



And there is one important detail in this: basically cause and effect invariance is guaranteed (mainly because if there is a rule that does something, there is always another rule that can override it).



So, now we can create a causal graph that will show an analogue of the theory of relativity in the space of rules. And this means that in the branch graph of the "rule space" we can expect the creation of different foliations, but they will all give consistent results.



This is a wonderful conceptual union. We have a physical space, a branch space, and now what we can call a rule space. And the same general ideas and principles apply to all of them. And just as we have defined frames of reference in physical space and space of ramifications, we can also define frames of reference in space of rules.



But what frames of reference can observers establish in the rule space? Typically, we can think of different frames of reference in the space of rules as corresponding to different languages ​​of description in which an observer can describe his experience of the universe.



In the abstract, it is a familiar idea that with any particular description language, we can always explicitly program any general-purpose computer to translate it into another description language. But here we are talking about the fact that in the space of rules it is enough to choose another frame of reference so that in our representation of the Universe a different language of description is used.



And the approximate reason this works is that different rule space foliations correspond to different choices of rule sequences in the rule space branch graph, which can in fact be configured to "compute" the output that would be obtained with any given language description ... That this might work ultimately depends on the fact that our rule sequences can support universal computation - simply “choose a different frame of reference in the rule space”, “run a different program” and get a different description of the observed behavior of the universe. ...



A strange but rather interesting picture. The universe uses every possible rule. But as beings embedded in the universe, we choose a particular foliation (or sequence of frames of reference) to understand what's going on. And this choice of foliation is consistent with a description language that gives us a specific way to describe the universe.



But what can be said for sure about the universe - regardless of foliation? There is one important circumstance: the universe, no matter what foliation is used to describe it, is just a universal computer and nothing more. And such hypercomputing is impossible in the universe.



Given the structure of our models, that's not all. In the same way as there is maximum speed in physical space (speed of light c) and the maximum speed in the space of ramifications (the maximum speed of entanglement ζ ), so there should also be the maximum speed in the space of rules, which we can call ρ - this is actually another fundamental constant of nature. (The constancy of ρ is in fact a reflection of the computational equivalence principle.)



But what does movement in the space of rules correspond to? In essence, this is a rule change. And to say that this can only happen at a finite speed is to say that there is computational irreducibility: one rule cannot imitate another infinitely fast. And given this final "emulation speed" there are "emulation cones", which are analogous to light cones and determine how far one can advance in the rule space in a certain time.



What units does ρ? Basically, it is the length of the program divided by the time. But while it is generally assumed in computation theory that the length of a program can be scaled almost arbitrarily by various computation models, here it is a measure of the length of a program that is somehow fundamentally tied to the structure of the branch system of the rule space and the physical space. (By the way, the analogue of curvature and Einstein's equations will also be in the space of rules - and this probably corresponds to the geometrization of the theory of computational complexity and questions such as P? = NP.)



More can be said about the structure of the rule space. For example, let's say we are trying to create a foliation in which we freeze time somewhere in the rule space. This would be consistent with trying to describe the universe using some kind of computationally reducible model - and it will get harder and harder to do this over time, as emulation cones provide more and more computational irreducibility.



So what does this all mean for our original goal of finding a rule to describe our universe? Basically, this says that any (universal computation) rule will do - as long as we are ready to create an appropriate description language. But the point is that we have basically already defined at least some elements of our language of description: these are the things that our senses discover, our measuring devices measure, and our existing physics describes. So, now our task is to find a rule that successfully describes our universe within this concept.



For me, this is a very satisfying solution to the mystery of why a particular rule was chosen for our universe. The answer is that ultimately there is no particular rule — any rule capable of universal computation will do. It's just that with some specific way of describing that we choose to use, there will be some specific rule that describes our universe. And in a sense, whatever feature is in this rule, it is simply a reflection of the specifics of our way of describing. In fact, the only thing that is special for us in the Universe is ourselves.



And this gives an unambiguous answer to another long-standing question: could there be other universes? The answer in our model is mostly negative. We cannot just "choose a different rule and get a different universe." Because in a sense, our universe already contains all the possible rules. (There may be other universes that do different levels of hypercomputing.)



But something weirder is also possible. While we look at our universe - and at reality - through our particular type of descriptive language, there are an infinite number of other possible descriptive languages ​​that can lead to descriptions of reality that seem coherent (and even, in some appropriate definition, “meaningful”) within themselves. themselves, but which will seem to us to correspond to completely incoherent and meaningless aspects of our universe.



I have always assumed that any entity that exists in our universe should at least "experience the same physics as we do." But now I understand that it is not so. In fact, there is an almost infinite variety of different ways of describing and perceiving our universe, or, in fact, an almost infinite variety of different "planes of existence" for entities in the universe - corresponding to different possible frames of reference in the space of rules, ultimately interconnected through general-purpose computing and rule space relativity.

The language of the universe

What does it mean to create a model of the universe? If we just want to know what the universe is doing, then we have the universe and we can just watch what it does. But when we talk about creating a model, what we really mean is that we want to have an idea of ​​the universe that somehow connects it to what we (humans) can understand. When computational irreducibility is taken into account, we do not expect the model to "predict" in advance the behavior of the universe down to every detail. But we really want to be able to point to a model - the structure of which we understand - and then be able to say that this model corresponds to our universe.



In the previous section, we said that we want to find a rule that we could in some sense relate to the description language that we use for the Universe. But what should be the language for describing the rule itself? There is inevitably a large computational distance between the basic rule and the features of the universe that we are used to describing. So, as I have said several times here in various ways, we cannot expect to use the usual concepts with which we describe the world (or physics) directly in constructing the rule.



I have spent most of my life as a language designer, mostly building what is now a fully fledged computational language, the Wolfram Language. And now I see the attempt to find a fundamental theory of physics as, in many ways, just another problem in language design - perhaps even the most important of such problems.



In developing a computational language, we are trying to create a bridge between two domains: the abstract world of computing and the "mental" world of what people understand and are interested in. There are all sorts of computational processes that can be devised (say, running randomly selected rules of a cellular automaton), but the main goal of language design is to figure out which ones are of concern to people at a given stage in human history, and then let people describe them.



Ok, let's talk about creating a model of the universe. Perhaps the most important idea in my attempts to find a fundamental theory of physics is that the theory should be based on a general computational paradigm (and not, for example, specifically on mathematics). So when we talk about a language for describing our model of the universe, we see that it must connect three different areas. It should be a language that people can understand. It must be a language capable of expressing computational ideas. And it should be a language that can truly represent the basic structure of physics.



So what should this language be? What primitives should it contain? The story that led me to what I am describing here is largely the story of my attempts to formulate the appropriate language. Are these cubic graphs? Are they ordered graphs? Are these rules applicable to abstract relationships?



In many ways, we are inevitably at the edge of the capabilities of the human mind. Perhaps one day we will develop familiar ways of talking about the concepts involved. But we don't have them yet. What has made this project feasible now is that we've come so far in developing ways to express computational ideas - and that, thanks to the Wolfram Language, these forms of expression are familiar, at least to me.



In an effort to serve human needs, the Wolfram Language first accepts input, evaluates it through computation, and then generates output. But that's not what the universe is doing. The universe, in a sense, contributed at the very beginning, but now it is just making an estimate - and with all our notions of foliations in mind, we select certain aspects of this current estimate.



This is a computation, but it is a computation performed in a way that is not familiar to us. For a language designer like me, this is interesting on its own, with all its scientific and technological side effects. It may take many more ideas before we can finish the job of finding a way to represent the basic rule of fundamental physics.



But I am optimistic: we already have almost all the ideas we need. We also have a good methodology: we can conduct research using computer experiments. If we were all to rely on the traditional methodology of mathematics, we could only explore what we already know. But by doing computer experiments, we are actually sampling the raw computational universe of possibilities, not limited to our existing understanding.



Of course, as with physics experiments, it is important how we think about our experiments and what language of description we use. It certainly helps that I have been doing computer experiments for over forty years, during which time I have been able to gradually improve my art and the science behind it.



This is similar to how we learn from our own experience in the physical world. By observing the results of many experiments, we gradually develop intuition, which, in turn, allows us to begin to create a conceptual framework, which is then used in developing our language to describe reality. But experiments must be carried out constantly. In a sense, computational irreducibility means that we will constantly receive surprises, which I find in practice in this project.



Can we combine physics, computation, and human understanding to create what we can regard as the ultimate fundamental theory of physics? It's hard to say how difficult it will be. But I am extremely optimistic and think that we are finally on the right track and have even solved the fascinating problem of language design needed to solve the mysteries of the universe.

In search of a fundamental theory!

With all this in mind, what needs to be done to find a fundamental theory of physics? Most importantly, we are finally on the right track. Of course, not surprisingly, the task is still technically extremely difficult. Part of this difficulty stems directly from computational irreducibility and from the difficulty of developing the consequences of the ground rules. But part of the difficulty is also related to the success and complexity of existing physics.



Ultimately, our goal should be to build a bridge that connects our models to existing knowledge of physics. And hard work lies ahead on both sides. Try to formulate the consequences of our models in terms consistent with existing physics, and try to formulate the mathematical structures of existing physics in terms that are consistent with our models.



For me, one of the most enjoyable aspects of our discoveries over the past couple of months has been the extent to which they eventually resonated in the vast range of existing - sometimes still seemingly 'purely mathematical' - directions that have moved from mathematics to physics in recent years. ... It seems that the creators of all modern theories were right from the beginning, and you just need to add some new substrate to see how they all fit together. Our models have hints of string theory, holographic principles, causal set theory, loop quantum gravity, twistor theory, and more. There are also modern mathematical ideas - geometric group theory, higher order category theory, non-commutative geometry, geometric complexity theory, etc.- which seem to fit so well with our models that one might think they had to be built specifically to analyze them.



I must say I did not expect this. The ideas and methods on which our models are based are very different from those that have ever been seriously applied in physics or even mathematics. But somehow - and I think this is a good sign - what has been found fits perfectly with a lot of recent work in physics and mathematics. The foundations and motivating ideas are different, but the methods (and sometimes even the results) often seem immediately applicable.



There is something else that I did not expect, but which is very important. When I studied cellular automata in the computational universe of simple programs, I usually found that computational irreducibility - and things like undecidability - are everywhere. You try complex mathematical methods and they almost always fail.



But because our models of fundamental physics are so minimalistic and structureless, even before facing the problem of irreducibility, we can see an amazing wealth of properties in our models. Hence many of our recent discoveries. And this is where the existing methods of physics and mathematics can make a great contribution. We can understand a lot before we face computational irreducibility. (Which, by the way, is probably the reason why we are even able to form a coherent representation of physical reality.)



So how will trying to find a fundamental theory of physics work in practice? We are planning a centralized effort to promote the project, using essentially the same research and development methods that we have developed at Wolfram Research over the past three decades and that have successfully brought us so many discoveries. We plan to do everything completely openly. We have already published the full suite of software tools we have developed , as well as nearly a thousand archived work records from the 1990s and over 400 hours of video from recent work sessions.



We want to allow people to participate directly in our centralized efforts or separately from us. We will broadcastwhat we do and maximize engagement. We will be running many educational programs . We also plan to conduct (live) working sessions with other people and groups, as well as provide channels for computerized publication of results and intermediate conclusions.



I must say that working on this project both now and in the past years has brought a lot of pleasure. And I hope that other people will be able to share these feelings as our project progresses. I think we have finally found a way to a fundamental theory of physics. And now let's go down this path. Let's try to finally figure out how our universe works!