Your squares are wrong

The other day there was an article devoted to the difference between a square with rounded edges and a "square circle" - an intermediate figure between a circle and a square, obtained from the superellipse formula . Readers' opinions were divided - not everyone saw the difference, and who saw - not everyone preferred the "correct" option. And I suspect why: those squares of yours are not real!

Alternative solution

My solution (in polar coordinates) turned out like this:

$$

$$\rho =\sqrt{\frac{2}{1+\sqrt{1+\left(\frac{1}{k^4}-\frac{2}{k^2}\right) \sin ^2(2 \phi )}}}$$

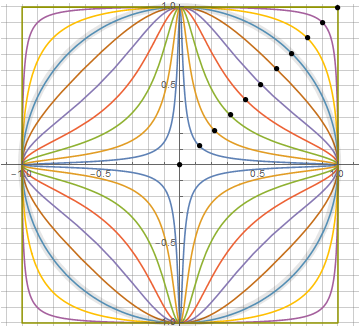
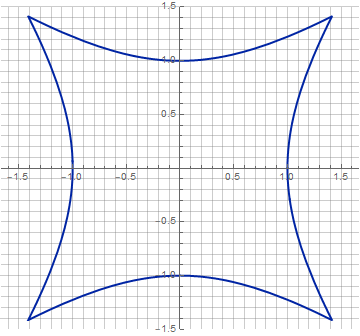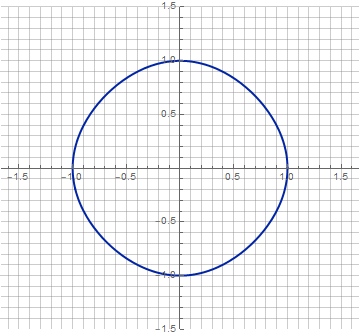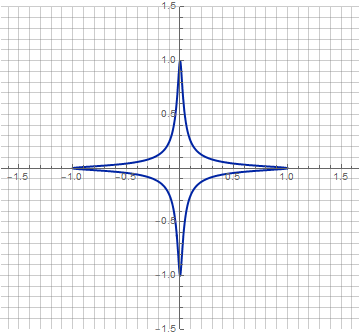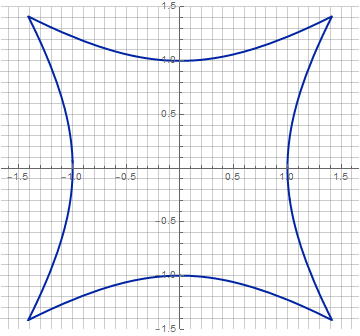
in which parameter $$$k$from 0 to 1 sets the degree of "squaring", and linearly - defining the point of intersection ( k , k ) of the figure with the diagonal. This means that we can uniquely define our square circle through 3 points. And yes, with$$$k = 1$we have a real square, with straight sides and sharp corners. Well, the circle, respectively, is obtained when$$$k = \frac{1}{\sqrt{2}}$(cosine 45 °). Variants of the resulting figures are reflected on the KDPV.



You can also note that this formula does not have such tricks as modulus functions, sign / discard, and so on - as is required for a superellipse. Everything is fair, only standard mathematical functions, with which there will be no difficulty in differentiating or integrating. By the way, about integration - if you wish, you can also find the area of ​​these figures (via elliptic integrals):

$$

$$\frac{4 k^4 E\left(\frac{2 k^2-1}{k^4}\right)-4 \left(k^2-1\right)^2 K\left(\frac{2 k^2-1}{k^4}\right)}{2 k^2-1}$$

Development

You can add more variation to the resulting shapes. For example, like this:

$$

$$\rho =\sqrt{\frac{1+\sqrt{\frac{(z-2)^2}{z^2}}}{1+\sqrt{1+\left(\frac{1}{k^4}-\frac{2}{k^2}\right) \sin^2(2\phi)+\left(\frac{4(1-z)}{z^2}\right)\cos^2(2 \phi)}}}$$

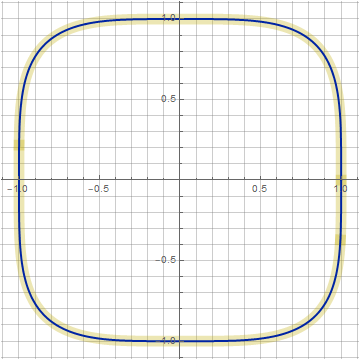
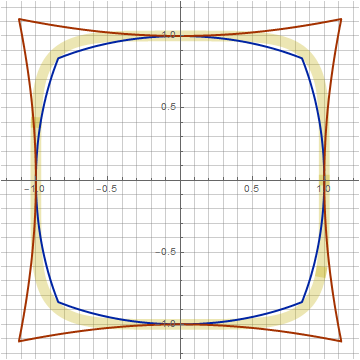
Here we have one more parameter z , which allows us to distort the figure without violating the ideology of construction. With its help, you can bring our figure closer to the superellipse (shown in yellow on the graphs). For example, for n = 4 ( k = 0.266, z = 0.1), the match is almost perfect:







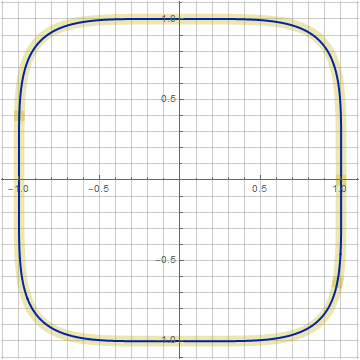
at higher n, the difference is already more noticeable ( n = 5, k = 0.6, z = 0.48):







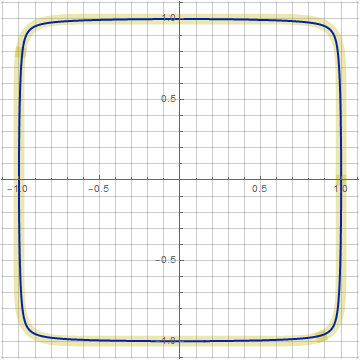
n = 10, k = 0.942, z = 1.02:





And yes, you can go in a completely radical way! This icon design certainly cannot be confused with anything:







Well, you can also dream up a little with animation:

Conclusion

If a certain designer of a certain company with (optionally) a fruit logo wants to get a unique design, even if it does not differ fundamentally from existing solutions, perhaps it is worth trying to look for and patent a really new formula, and not attract a long-known solution by hanging tons of marketing bullets on it ... Especially if it can be done just for fun by a simple person from the provinces without special education.



PS Sources of the article are here .



PPS Through the equation of the curve in Cartesian coordinates, the original formula will look like

$$

$$0=-2+\left(x^2+y^2\right) \left(1+\sqrt{1+\frac{\left(4-8 k^2\right) x^2 y^2}{k^4 \left(x^2+y^2\right)^2}}\right)$$