2nd order circular curves

As you know , Bezier curves cannot construct an arc of a circle or an ellipse. This article discusses curves that do not have this disadvantage.

Bezier Curves

The logic behind the construction of Bezier curves is well understood from the following animation:







To get the formula directly from the graphical representation, it is enough to define an auxiliary function for linear interpolation between two points, at which, when the parameter t changes from 0 to 1, it returns intermediate values ​​from a to b :

$$

$$mix(a,b,t) =a (1-t)+b t$$

With its help, you can consistently find the necessary points - first find

$$

$$ac = mix(a, c, t)$$

and

$$

$$cb = mix(, b, t)$$

and then through them find

$$

$$d = mix(ac, cb, t)$$

If you wish, you can substitute the functions into each other and shorten - although this will not particularly simplify the calculations, it will allow you to generalize the curves to an arbitrary number of control points (via Bernstein polynomials). In our case, we get

$$

$$d = a (1-t)^2+b t^2+2 c t (1-t)$$

Increasing the order of the curves is achieved trivially - the initial points are not set constant, but as a result of interpolation between n + 1 other control points:

Circular curves

Arc of a circle

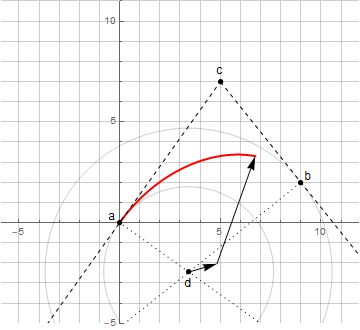
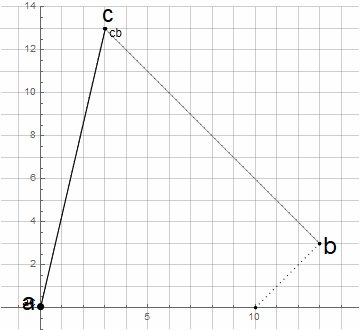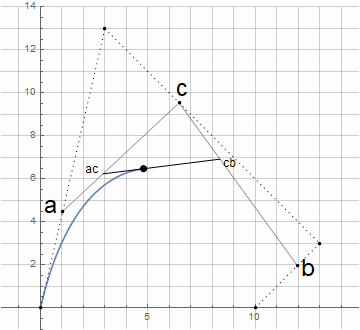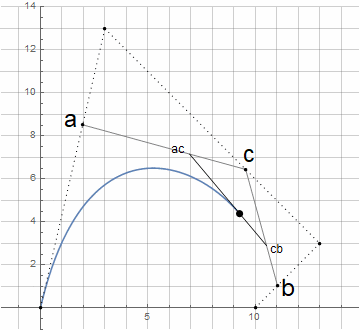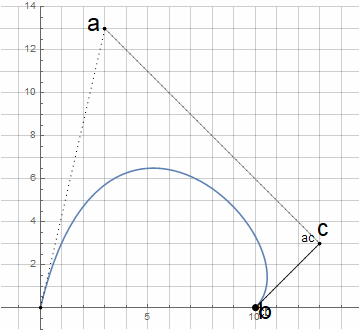
To build an arc of a circle in a similar way, it is necessary to determine the appropriate construction logic - by analogy with drawing a circle with a compass.





Initially, we do not know the center of the circle d - it is found through the intersection of the perpendiculars to the tangents at points a and b (hereinafter nodal); the tangents themselves are specified using point c (hereinafter referred to as the guideline). To create an arbitrary circular arc (less than 180 °), it is sufficient that the distances from the direction point to the nodal points are the same.

Ellipse arc

Constructing an ellipse arc is already more difficult - you need two vectors rotating in different directions ( more details here )





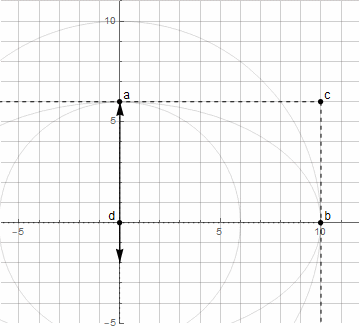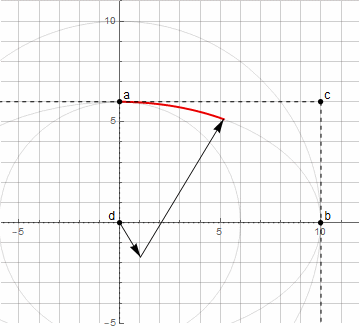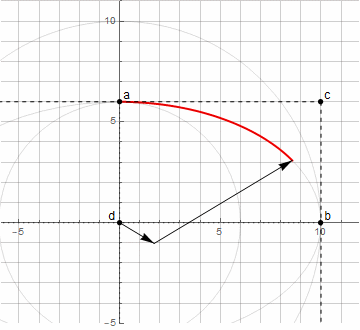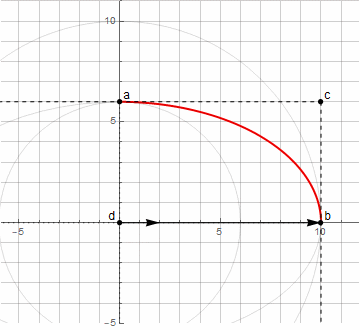
Using the above method of finding the point d , we can no longer build an arbitrary arc of an ellipse - only from 0 ° to 90 ° (including rotated by a certain angle).

Arc hypotrochoid

Setting the condition that at the beginning and end of the drawing the vectors must lie on one straight line, we get the arc of the hypotrochoid in all other cases. This condition is not accidental and (besides the unique definition of the curve) guarantees the coincidence of the tangents at the nodal points. As a consequence, the angular paths that both vectors travel will be different, but still add up to 180 °.





How the shape of the curve changes depending on the position of the guide point can be seen in the following animation:

Algorithm

Since here we have rotations on a two-dimensional plane, it is convenient to describe the mathematics of constructing these curves in terms of complex numbers.



1) find the point of intersection of the normals of the tangents drawn from the direction point to the nodal points:

$$

$$d=\frac{(2 a-c) (c-b) a^*+ (2 b-c) (a-c) b^*-c (a-b) c^*}{(c-b)a^*+(a-c) b^*-(a-b) c^*}$$

(here the asterisk means complex conjugation).



2) knowing d , we find the lengths of the normals

$$

$$r_{\text{ad}}=\left| a-d\right|$$

$$

$$r_{\text{bd}}=\left| b-d\right|$$

and their sum and difference

$$

$$r_m=\frac{1}{2} \left(r_{\text{ad}}+r_{\text{bd}}\right)$$

$$

$$r_s=\frac{1}{2} \left(r_{\text{ad}}-r_{\text{bd}}\right)$$

3) find the unit vector from which the construction begins

$$

$$v=\frac{a-d}{\left| a-d\right| }$$

4) find the angular paths that each of the vectors must pass

$$

$$\phi _m=\arg \left(\frac{a-d}{b-d}\right)$$

$$

$$\phi _s=\arg \left(-\frac{a-d}{b-d}\right)$$

5) successively changing t from 0 to 1 with some step, we find the point belonging to the curve by the formula

$$

$$d+v \left(r_m e^{-i t \phi _m}+r_s e^{-i t \phi _s}\right)$$

Circular splines

Just like Bézier curves, these curves can be combined to create piecewise continuous splines. To ensure smoothness at the anchor points (docking), the anchor point must be in line with two adjacent direction points. To do this, you can specify anchor points not explicitly, but through the interpolation of the direction points. They can also not be specified at all, calculating completely automatically - for example, as the average between the guide points:







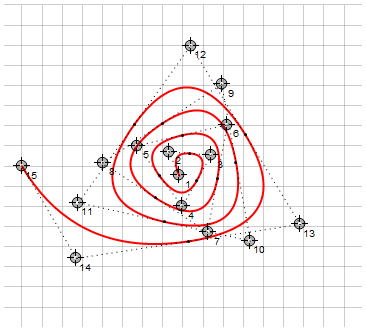
On the right, for comparison, the same approach was used with 2nd order Bezier curves.

Notes and nuances

Unlike Bezier curves, here the curve does not always lie within the shape of the lines connecting the control points, for example





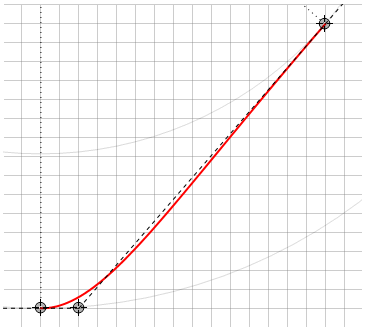
In addition, there is a degenerate case that needs to be handled separately - when the direction point lies on the same line with the anchor points. In this case, the curve degenerates into a straight line, and when trying to calculate the point d , division by zero occurs.



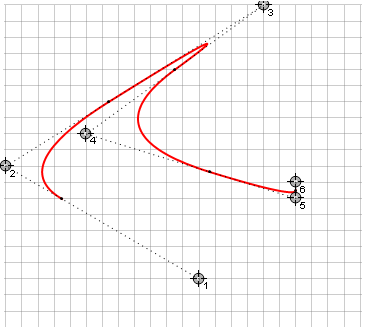
These curves also have restrictions on the curvature of the line, because the algorithm chooses the smallest path to follow and the curve cannot go around more than 180 °. This leads to the fact that with piecewise continuous interpolation, sharp corners can occur at a certain position of the direction points (on the right - the same points for Bezier):

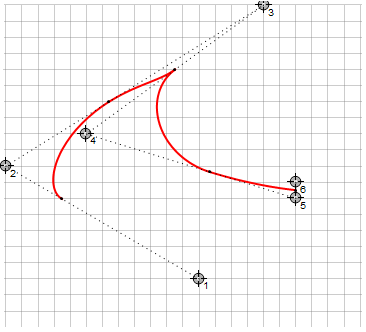
Conclusion

Further development of the considered method of constructing curves is an increase in the number of vectors involved in the construction of the curve and, accordingly, an increase in the number of direction points. However, unlike Bezier curves, the increase in order is not obvious here and requires a separate thoughtful reflection. Various methods of combining them with Bezier curves are also possible - in particular, interpolation of the center of the circle of drawing vectors.



The considered method of constructing curves is also not the only one, a particular case of which are arcs of a circle and an ellipse - at least an ellipse can be constructed through the intersection of straight lines in a parallelogram(however, the author failed in this version). It is possible that there are other solutions, including options described in the article - write in the comments if you know something on this topic.



The source code for the article can be downloaded from GitHub .