Let's see what solutions this problem has.
Distribution of objects "by capacity"
In order not to delve into uninteresting abstractions, we will consider it using the example of a specific task - monitoring . I am sure that you will be able to relate the proposed methods to your specific tasks yourself.
"Equivalent" monitoring objects
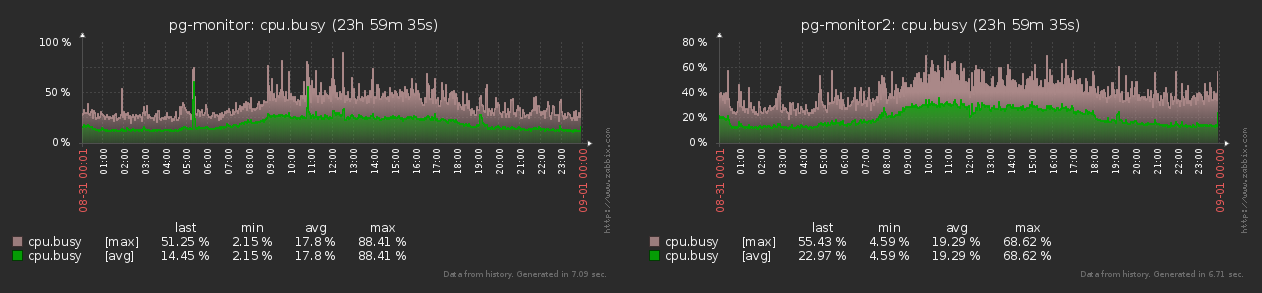
An example is our metric collectors for Zabbix , which historically share a common architecture with PostgreSQL log collectors. Indeed
, each monitoring object (host) generates for zabbix almost stably the same set of metrics with the same frequency all the time:
As you can see in the graph, the difference between the min-max values of the number of generated metrics does not exceed 15% . Therefore, we can consider all objects to be equal in the same "parrots" .
Strong "imbalance" between objects
Unlike the previous model, the monitored hosts are far from homogeneous for the log collectors .
For example, one host can generate a million plans per day in the log, another tens of thousands, and some - even just a few. And the plans themselves are very different in terms of volume and complexity and in terms of distribution over the time of day. So it turns out that the load "shakes" strongly , at times:

Well, since the load can change so much, then you need to learn how to manage it ...
Coordinator
We immediately understand that we obviously need to scale the collector system, since one separate node with the entire load will someday cease to cope. And for this we need a coordinator - someone who will manage the entire zoo.
It turns out something like this:

Each worker his load "in parrots" and as a percentage of the CPU periodically resets the master, those - to the collector. And he, on the basis of these data, can issue a command such as "put a new host on an unloaded worker # 4" or "hostA must be transferred to worker # 3" .
Here you also need to remember that, unlike monitoring objects, the collectors themselves do not have equal "power" at all - for example, on one you may have 8 CPU cores, and on the other - only 4, and even a lower frequency. And if you load them with tasks "equally", then the second will start to "shut up", and the first will be idle. Hence it follows ...
Coordinator's tasks
In fact, there is only one task - to ensure the most even distribution of the entire load (in% cpu) among all available workers. If we can solve it perfectly, then the uniformity of the% cpu-load distribution over the collectors will be obtained automatically.
It is clear that even if each object generates the same load, over time, some of them may "die off", and some new ones appear. Therefore, you need to be able to manage the entire situation dynamically and maintain a balance constantly .
Dynamic balancing
We can solve a simple problem (zabbix) quite trivially:
- we calculate the relative capacity of each collector "in tasks"
- divide all tasks between them proportionally
- we distribute evenly between workers

But what to do in case of "strongly unequal" objects, like for a log collector? ..
Uniformity assessment
Above, we used the term " maximally uniform distribution " all the time , but how can you formally compare two distributions, which one is "more uniform"?
For evaluating uniformity in mathematics, there has long been such a thing as the standard deviation . Who is lazy to read:
S[X] = sqrt( sum[ ( x - avg[X] ) ^ 2 of X ] / count[X] )Since the number of workers on each of the collectors can also differ for us, the load spread should be normalized not only between them, but also between the collectors as a whole .
That is, the distribution of the load over the workers of the two collectors
[ (10%, 10%, 10%, 10%, 10%, 10%) ; (20%) ]is also not very good, since the first one turns out to be 10% , and the second - 20% , which, as it were, is twice as much in relative terms.
Therefore, we introduce a single metric-distance for a general estimate of "uniformity":
d([%wrk], [%col]) = sqrt( S[%wrk] ^ 2 + S[%col] ^ 2 )Modeling
If we had a few objects, then we could brute-force "decompose" them between workers so that the metric was minimal . But we have thousands of objects, so this method will not work. But we know that the collector can "move" an object from one worker to another - let's model this option using the gradient descent method .
It is clear that we may not find the “ideal” minimum of the metric, but the local one is for sure. And the load itself can vary so much over time that there is absolutely no need to look for an "ideal" for an infinite time .
That is, we just need to determine which object and to which worker is most efficient to "move". And let's make it a trivial exhaustive modeling:
- ( host, worker)
- host worker' «»
«» . - « »
- d «»
We line up all pairs in ascending order of the metric . Ideally, we should always implement the transfer of the first pair , as it gives the minimum target metric. Unfortunately, in reality, the transfer process itself "costs resources", so you should not run it for the same object more often than a certain "cooling" interval .
In this case, we can take the second, third, ... pair by rank - if only the target metric would decrease relative to the current value.
If there is nowhere to decrease - here it is a local minimum!
Example in the picture:

It is not at all necessary to start iterations "all the way". For example, you can do an averaged load analysis over a 1 minute interval, and upon completion, do a single transfer.
Micro-optimizations
It is clear that an algorithm with complexity
T() x W()is not very good. But in it you should not forget to apply some more or less obvious optimizations that can speed it up at times.
Zero "parrots"
If an object / task / host has generated a load of "0 pieces" on the measured interval , then it is not something that can be moved somewhere - it does not even need to be considered and analyzed.
Self-transfer
When generating pairs, there is no need to evaluate the efficiency of transferring an object to the same worker , where it is already located. After all, it will already be
T x (W - 1)- a trifle, but nice!
Indiscernible load
Since we are modeling the transfer of the load, and the object is just a tool, there is no point in trying to transfer the "identical"% cpu - the values of the metrics will remain exactly the same, albeit for a different distribution of objects.
That is, it is enough to evaluate a single model for the tuple (wrkSrc, wrkDst,% cpu) . Well, and you can consider “equal”, for example,% cpu values that match up to 1 decimal place.
JavaScript example implementation
var col = {
'c1' : {
'wrk' : {
'w1' : {
'hst' : {
'h1' : 5
, 'h2' : 1
, 'h3' : 1
}
, 'cpu' : 80.0
}
, 'w2' : {
'hst' : {
'h4' : 1
, 'h5' : 1
, 'h6' : 1
}
, 'cpu' : 20.0
}
}
}
, 'c2' : {
'wrk' : {
'w1' : {
'hst' : {
'h7' : 1
, 'h8' : 2
}
, 'cpu' : 100.0
}
, 'w2' : {
'hst' : {
'h9' : 1
, 'hA' : 1
, 'hB' : 1
}
, 'cpu' : 50.0
}
}
}
};
// ""
let $iv = (obj, fn) => Object.values(obj).forEach(fn);
let $mv = (obj, fn) => Object.values(obj).map(fn);
// initial reparse
for (const [cid, c] of Object.entries(col)) {
$iv(c.wrk, w => {
w.hst = Object.keys(w.hst).reduce((rv, hid) => {
if (typeof w.hst[hid] == 'object') {
rv[hid] = w.hst[hid];
return rv;
}
// ,
if (w.hst[hid]) {
rv[hid] = {'qty' : w.hst[hid]};
}
return rv;
}, {});
});
c.wrk = Object.keys(c.wrk).reduce((rv, wid) => {
// ID -
rv[cid + ':' + wid] = c.wrk[wid];
return rv;
}, {});
}
//
let S = col => {
let wsum = 0
, wavg = 0
, wqty = 0
, csum = 0
, cavg = 0
, cqty = 0;
$iv(col, c => {
$iv(c.wrk, w => {
wsum += w.cpu;
wqty++;
});
csum += c.cpu;
cqty++;
});
wavg = wsum/wqty;
wsum = 0;
cavg = csum/cqty;
csum = 0;
$iv(col, c => {
$iv(c.wrk, w => {
wsum += (w.cpu - wavg) ** 2;
});
csum += (c.cpu - cavg) ** 2;
});
return [Math.sqrt(wsum/wqty), Math.sqrt(csum/cqty)];
};
// -
let distS = S => Math.sqrt(S[0] ** 2 + S[1] ** 2);
//
let iterReOrder = col => {
let qty = 0
, max = 0;
$iv(col, c => {
c.qty = 0;
c.cpu = 0;
$iv(c.wrk, w => {
w.qty = 0;
$iv(w.hst, h => {
w.qty += h.qty;
});
w.max = w.qty * (100/w.cpu);
c.qty += w.qty;
c.cpu += w.cpu;
});
c.cpu = c.cpu/Object.keys(c.wrk).length;
c.max = c.qty * (100/c.cpu);
qty += c.qty;
max += c.max;
});
$iv(col, c => {
c.nrm = c.max/max;
$iv(c.wrk, w => {
$iv(w.hst, h => {
h.cpu = h.qty/w.qty * w.cpu;
h.nrm = h.cpu * c.nrm;
});
});
});
// ""
console.log(S(col), distS(S(col)));
//
let wrk = {};
let hst = {};
for (const [cid, c] of Object.entries(col)) {
for (const [wid, w] of Object.entries(c.wrk)) {
wrk[wid] = {
wid
, cid
, 'wrk' : w
, 'col' : c
};
for (const [hid, h] of Object.entries(w.hst)) {
hst[hid] = {
hid
, wid
, cid
, 'hst' : h
, 'wrk' : w
, 'col' : c
};
}
}
}
// worker
let move = (col, hid, wid) => {
let w = wrk[wid]
, h = hst[hid];
let wsrc = col[h.cid].wrk[h.wid]
, wdst = col[w.cid].wrk[w.wid];
wsrc.cpu -= h.hst.cpu;
wsrc.qty -= h.hst.qty;
wdst.qty += h.hst.qty;
// "" CPU
if (h.cid != w.cid) {
let csrc = col[h.cid]
, cdst = col[w.cid];
csrc.qty -= h.hst.qty;
csrc.cpu -= h.hst.cpu/Object.keys(csrc.wrk).length;
wsrc.hst[hid].cpu = h.hst.cpu * csrc.nrm/cdst.nrm;
cdst.qty += h.hst.qty;
cdst.cpu += h.hst.cpu/Object.keys(cdst.wrk).length;
}
wdst.cpu += wsrc.hst[hid].cpu;
wdst.hst[hid] = wsrc.hst[hid];
delete wsrc.hst[hid];
};
// (host, worker)
let moveCheck = (orig, hid, wid) => {
let w = wrk[wid]
, h = hst[hid];
// -
if (h.wid == w.wid) {
return;
}
let col = JSON.parse(JSON.stringify(orig));
move(col, hid, wid);
return S(col);
};
// (hsrc,hdst,%cpu)
let checked = {};
// ( -> )
let moveRanker = col => {
let currS = S(col);
let order = [];
for (hid in hst) {
for (wid in wrk) {
// ( 0.1%) ""
let widsrc = hst[hid].wid;
let idx = widsrc + '|' + wid + '|' + hst[hid].hst.cpu.toFixed(1);
if (idx in checked) {
continue;
}
let _S = moveCheck(col, hid, wid);
if (_S === undefined) {
_S = currS;
}
checked[idx] = {
hid
, wid
, S : _S
};
order.push(checked[idx]);
}
}
order.sort((x, y) => distS(x.S) - distS(y.S));
return order;
};
let currS = S(col);
let order = moveRanker(col);
let opt = order[0];
console.log('best move', opt);
//
if (distS(opt.S) < distS(currS)) {
console.log('move!', opt.hid, opt.wid);
move(col, opt.hid, opt.wid);
console.log('after move', JSON.parse(JSON.stringify(col)));
return true;
}
else {
console.log('none!');
}
return false;
};
// -
while(iterReOrder(col));As a result, the load on our reservoirs is distributed almost the same at each moment of time, promptly leveling the emerging peaks: