By translating Keller's hypothesis into a computer-understandable graph search language, the researchers finally solved the problem of covering spaces with tiles

A team of mathematicians have finally figured out Keller's hypothesis - but not on their own. Instead, they trained a whole fleet of computers, and they solved it.
Keller's hypothesis, put forward 90 years ago by Ott-Heinrich Keller, is related to the task of covering spaces with identical tiles. She argues that if you pave a two-dimensional space with two-dimensional square tiles, then at least two of them will have to touch sides completely, and not partially. The hypothesis makes the same prediction for any dimensions - that is, when filling a 12-dimensional space with 12-dimensional "squares", at least two of them must have a common edge.
For years, mathematicians fought over this hypothesis, proving its truth for some dimensions and false for others. And by last autumn the question remained unresolved only for seven-dimensional space.
But new computer-generated evidence solved that problem too. The proof , published last October, is one of the newest examples of the combination of human genius and sheer computing power to answer the most exciting questions in mathematics.
The authors of the new work, Joshua Breukensik of Stanford, Marin Hijul and John Mackey of Carnegie Mellon University, and David Narvaez of the Rochester Institute of Technology, solved this problem using 40 computers. In just 30 minutes, the machines gave a monosyllabic answer: yes, in seven dimensions, the hypothesis is correct. And we don't even have to take this conclusion on faith.
Attached to the answer is a long piece of evidence explaining its truth. The proof is too long for a human to understand, but another computer program can verify it.
In other words, even if we don't know exactly what computers did to prove Keller's hypothesis, we can at least make sure they did it right.
The mysterious seventh dimension
It is easy to see that Keller's conjecture is true in two dimensions. Take a piece of paper and try covering it with equal squares without gaps or overlap. Pretty soon you will realize that you can do this only if at least two squares have the same side. If you have cubes at hand, it will be easy for you to verify that the hypothesis is true for the third dimension. In 1930, Keller suggested that this relationship works for all dimensions and their corresponding tiles.
Early results supported Keller's prediction. In 1940, Oscar Perron proved that the hypothesis was correct for measurements one through six. However, more than 50 years later, a new generation of mathematicians found the first counterexample to this hypothesis: in 1992, Jeffrey Lagarias and Peter Shoreproved that the hypothesis does not work in the 10th dimension.

Keller's hypothesis predicts that when filling a space in any dimension, at least two tiles must completely touch sides.
When filling a two-dimensional space, many tiles have common sides (blue lines).
When filling 3D space, many cubes have common faces (blue).
It is easy to show that if a hypothesis fails in some dimension, it does not hold in all higher ones. Therefore, after the work of Lagarias and Shor, it remains only to resolve the issue for the seventh, eighth and ninth dimensions. In 2002, Mackey proved that Keller's hypothesis was false for dimension eight (and therefore nine).
Only the seventh dimension remained open - it was either the largest dimension for which this hypothesis is true, or the smallest in which the hypothesis is incorrect.
“Nobody knows exactly what is going on there,” said Khiyul.
Connect the dots
While mathematicians struggled with this problem for several decades, their methods gradually changed. Perron worked on the first six dimensions using only pencil and paper, but by the 1990s, researchers had figured out how to translate Keller's hypothesis into a completely different form - allowing them to use computers to solve it.
The original formulation of the Keller conjecture concerns smooth continuous space. In such a space, there are an infinite number of ways to place an infinite number of tiles. But computers are not good at solving problems with an infinite number of options - to cope with them, they need discrete and finite objects.

Marin Hijul of Carnegie Mellon University
In 1990 Kereszteli Korradi and Sandor Shabo came up with a suitable discrete object. They showed that questions that are equivalent to Keller's hypothesis can be asked about this object. And if you prove something related to these objects, then the Keller hypothesis will be proved. This reduced the question of infinity to a less complex arithmetic problem with multiple numbers.
Here's how it works.
Let's say you want to deal with the Keller hypothesis in two dimensions. Corradi and Shabo came up with a method for this, using the construction of a structure, which they called the Keller graph.
To begin with, imagine that there are 16 dice on the table, and all of them have an upper edge with two dots (two dots denote a two-dimensional space, and why there are 16 cubes - we will see a little later). All cubes are rotated in the same way, so that the two points are located the same for everyone. Color each dot with any of four colors: red, green, white, or black.
The points on one cube do not change places - let one of them denote the x coordinate, and the other - y. Having colored the cubes, we begin to draw lines, or edges, between pairs of cubes if two conditions are met: the points in the same place for a pair of cubes have different colors, and in the other they are different and paired, and pairs are considered red with green, or black with white.
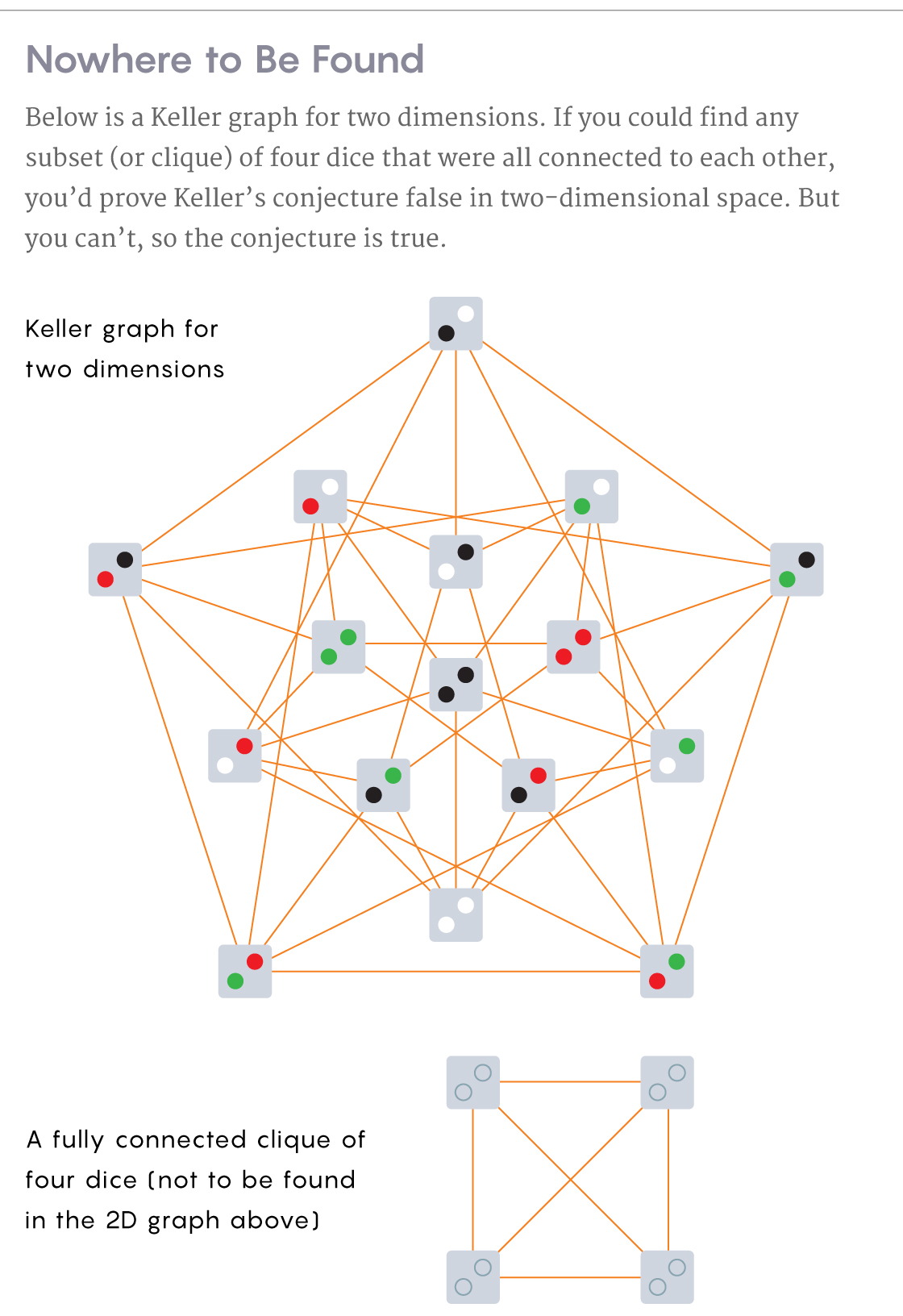
Keller graph for two dimensions. Finding a subset of four cubes in which each is connected to all the others, you will disprove Keller's hypothesis for two-dimensional space. However, there is no such subset, and the hypothesis is correct.
Below is an example of a fully merged clique of four dice that is not in the graph.
That is, for example, if one cube has two red dots, and the other has two black dots, they are not connected by an edge. Their points at the same positions have different colors, but they do not satisfy the requirement of pairing colors. If one cube has red and black dots, and the other has two green dots, they are connected by an edge, because in one position they have paired colors (red and green), and in the other they are simply different (black and green).
There are 16 ways to color two points with four colors (so we have 16 cubes). Lay out all these 16 possibilities in front of you. Connect all pairs of cubes that satisfy the requirements. Are there four cubes in your scheme, each of which is combined with three others?
Such a fully connected subset of cubes is called a clique. If you can find one, you will disprove the Keller hypothesis in two dimensions. However, you cannot - it simply does not exist. And the absence of such a clique of four cubes means that Keller's hypothesis is true for two dimensions.
These cubes are not literally the same tiles as Keller's hypothesis, however, you can assume that each cube represents a tile. Consider the colors assigned to the points as the coordinates that place the cube in space. And the existence of an edge is a description of how two cubes are positioned relative to each other.
If the colors of the cubes are the same, they represent tiles that are equally spaced in space. If they do not have common colors and color pairs (one has black and white, the other has green and red), they indicate partially overlapping tiles - which is not allowed in filling the space. If two cubes have one set of matching colors and one set of the same color (one red-black, the other green-black), they represent tiles with a common side.
Finally, and most importantly, if they have one set of paired colors and another set of different colors - that is, if they are connected by an edge - then the cubes represent tiles that are in contact with each other, but slightly shifted, due to which their edges do not completely coincide ... It is this condition that we need to study. Cubes connected by an edge denote adjoining tiles that do not have a common side - this is the arrangement needed to refute Keller's hypothesis.
“They should touch, but not completely,” said Khiyul.

Same coloring - same arrangement.
Different colors, no pairs - overlapping.
Two paired colors and a pair of the same are the common side.
Two paired colors and two different - partial contact by the sides.
Scaling
Thirty years ago, Corradi and Schabo proved that mathematicians could use a similar procedure to work with Keller's hypothesis in any dimension, tweaking the parameters of the experiment. To prove the Keller hypothesis in three dimensions, you can use 216 cubes with three points on the edge, and possibly three pairs of colors (however, there is some flexibility here). Then you need to look for eight cubes (2 3 ), completely connected to each other, according to the same conditions that we gave above.
In general, to prove Keller's conjecture in n dimensions, you need to use cubes with n points and try to find a clique of size 2 n among them . It can be assumed that it represents a kind of super-tile (consisting of 2 nsmaller tiles) capable of covering the entire n-dimensional space.
If you can find this super-tile (which does not have tiles with a common side), you can use copies of it to cover the entire space with tiles without a common side, which will disprove Keller's hypothesis.
“If successful, you can cover the entire space with transference. A block without common tile sides will extend to the entire floor, ”said Lagarias, now at the University of Michigan.
Mackey refuted Keller's hypothesis in the 8th dimension, finding a clique of 256 cubes (2 8 ), so it remained to deal with the hypothesis in the 7th dimension, finding a clique of 128 cubes (2 7). Finding this clique will disprove the Keller hypothesis in the seventh dimension. Prove that it doesn't exist and you will prove the hypothesis is true.
Unfortunately, finding a clique of 128 cubes is an especially difficult task. In previous works, researchers took advantage of the fact that dimensions 8 and 10 can, in a sense, be "decomposed" into spaces of lower dimension, with which it is easier to work. And here this did not work.
“The seventh dimension is inconvenient because 7 is a prime number and you can't break it down into dimensions of a smaller order,” Lagarias said. “Therefore, there was no way out but to deal with the full-fledged combinatorics of these graphs.”
Finding a 128-cube clique can be challenging for the unaided brain - but these are the kinds of questions that computers are good at answering, especially with a little help.
The language of logic
To turn search for clicks into a task that a computer can handle, you need to formulate it in terms of propositional logic . This is a logical reasoning that includes a set of restrictions.
Let's say you three are planning a party with friends. You are trying to create a guest list, but there are conflicts of interest. Let's say you want to either invite Alexei or exclude Kolya. One of your friends wants to invite Kolya, or Vlad, or both. Another friend does not want to call either Alexei or Vlad. With such restrictions, is it possible to create a guest list that will satisfy all three?
In computer science terms, this problem is called the acceptability problem. It can be solved by describing the condition in the propositional formula. In this case, it looks like this, and A, K and B denote potential guests: (A OR NOT K) AND (K OR B) AND (NOT A OR NOT B).
The computer calculates it by substituting 0 or 1 in each variable. 0 is the value of the variable "false" or off, and 1 is "true" or on. Substituting 0 instead of A, we say that Alexei was not invited, and 1 that he was invited. In this simple formula, 0 and 1 can be substituted (by making a guest list) in many ways, and it is possible that after going through them all the computer will conclude that it is impossible to satisfy all interests. However, in this case, there are two ways to substitute 1 and 0 so as to please everyone: A = 1, K = 1, B = 0 (invite Alexey and Kolya) and A = 0, K = 0, B = 1 (invite one Vlad ).
The computer program that solves such statements is called the SAT solver, where SAT is short for satisfiability. It examines all combinations of variables and gives a monosyllabic answer - either YES, there is a way to satisfy the requirements of the formula, or NO, it is not.

John Mackie of Carnegie Mellon University
"You are just looking to see if you can assign true and false values to all variables so that the whole formula is true, and if yes, then it is satisfactory, and if not, then no," said Thomas Hales of University of Pittsburgh.
The question of finding a clique of 128 cubes is a similar problem. It can also be rewritten as a propositional formula and given to the SAT solver. Start with lots of dice with 7 dots each and 6 possible colors. Is it possible to color the dots so that 128 cubes are connected to each other according to certain rules? In other words, is it possible to assign colors so that the click appears?
The propositional formula for the clicked question is quite long and contains 39,000 variables. Each can be assigned one of two values, 0 or 1. As a result, the number of possible options for arranging values, or ways of assigning colors, was 2,39,000 - which is very, very much.
To find the answer to the question about the Keller hypothesis in seven dimensions, the computer would have to check all these combinations - and either exclude them all (which would mean that the clique of size 128 does not exist, and the Keller hypothesis in the seventh dimension is correct), or find at least would be one working option (disproving Keller's hypothesis).
“If you do a simple iteration of all the possibilities, you come across a 324-digit number,” Mackey said. The fastest computer in the world would work until the end of time, going through all the possibilities.
However, the authors of the new work figured out how a computer can give a definite answer without checking all the possibilities. The key to this is efficiency.
Hidden efficiency
Mackey recalls the day when, from his point of view, the project actually started working. He was standing in front of a blackboard in his office at Carnegie Mellon University, discussing an issue with two coauthors, Hijul and Breikensik, when Hijul proposed a way to structure the search so that it could be completed in a reasonable amount of time.
“There was a real human genius working in my office that day,” Mackey said. - I was like watching Wayne Gretzky, or LeBron James in the NBA Finals. I have goosebumps from just the memory of it. "
You can tailor searches for a specific Keller graph in different ways. Imagine you have a lot of cubes on your table and you are trying to solve 128 of them, following the rules of Count Keller. Let's say you have selected 12 correctly, but you can't figure out how to add the next one. At this point, you can discard any configuration of 128 dice that includes this non-working configuration of 12.
“If you know that your first five assignments don't match, you don't have to look for other variables, and this usually cuts down on the search field a lot,” said Shore, now at MIT.
Another type of efficiency is associated with symmetry. Symmetrical objects are somewhat the same. Identity allows us to understand the whole object as a whole, studying only a part of it - looking at half of a person's face, you can restore it in its entirety.
Similarly, you can cut corners in the case of Keller graphs. Imagine again that you are trying to line up the cubes on the table. Let's say you start at the center of the table and build your hand on the left. You lay out four dice and you come to a dead end. You have now eliminated one starting combination and all combinations based on it. However, you can exclude the mirroring of this initial combination - the configuration of the cubes that you get if you place them in the same way, only on the right.
“If you came up with a way to solve satisfactory problems that cleverly takes into account symmetry, you have greatly simplified the task,” said Hales.
Four colleagues took advantage of the efficiencies of this search in a new way - in particular, they automated the consideration of symmetric cases, while mathematicians previously processed them almost manually.
As a result, they improved their search for cliques of size 128 so much that instead of checking 2,39,000 configurations, their program had to check only about a billion ( 2,30 ). This made a search that could take forever into a task for one morning. Finally, after only half an hour of calculations, they received an answer.
“The computers said no, so we know the hypothesis works,” Hiyul said. It is impossible to color the 128 cubes so that they all merge with each other, so Keller's hypothesis for the seventh dimension is confirmed. For any placement of tiles covering a space, there will inevitably be at least a pair of completely touching edges.
The computer gave not just a monosyllabic answer. He attached to it a long 200 GB proof supporting this conclusion.
The proof is not just a computation of all the sets of variables that have been verified by a computer. This is a logical argument proving that the necessary clique cannot exist. The researchers fed the evidence into a program that tests formal evidence by tracing the logic of the argument and validated it.
“We didn't just go through all the options and didn't find anything. We went through all the options and were able to write down proof that such a thing does not exist, ”Mackey said. "We were able to record the evidence of dissatisfaction."