
, , . , , , . , , .
, ,
, , , 17. , ?
, 1 N , .
« » , . , , , , 34, "x2" 17. «»: 17. , - . , 17 34, "x1" "x2" — , , , .
- ? , , . , 30 . «30» — ? , 1000 , 999 30 , — 17. , 30- , 17- — ? , , , , , , , , - .
, , , .
, ,
, .
: , , , . , , , , , . , : . ?
, :
- .
- , , .
- , , . «1» «2», , «3», «4», «5» «6» — .
- , . , «», , «» — .
1) , . , , , 1). , , , 1) , .
, 2) «», , , , .
, . , , , 1/3, , , — 2/3. , 3) — , . , . , , , 1000 , , , , , . , 3), , .
, : , , 50%. , , , . , . 4) , , .
, , . , , , , 4. , , - .
«»
, , : , - , , , . , , , , . , , .
: « , ?»
« » , "x1" "x2".
, . , . , .
"x1" . , , , . : , , , . 50%, — . , "x1" () , .
, "x2". , , . , , , , . , , , . 4- , — . , "x2", , () 3/4 , .
, , , , , , , . , . , , 0 π, . .
, , . . , . , , , , , . , , , .
, "x1" - 50%, "x2" — 75% , , .
- . , , , , , , — , .
, , — , . , , . , , , . , «» , , .
, ,
. , ( ), . , : . , , , . , , , , , «». , ,
.
, .
, , — () , — . , , ? , , — , — .
, , . , : ( 1)
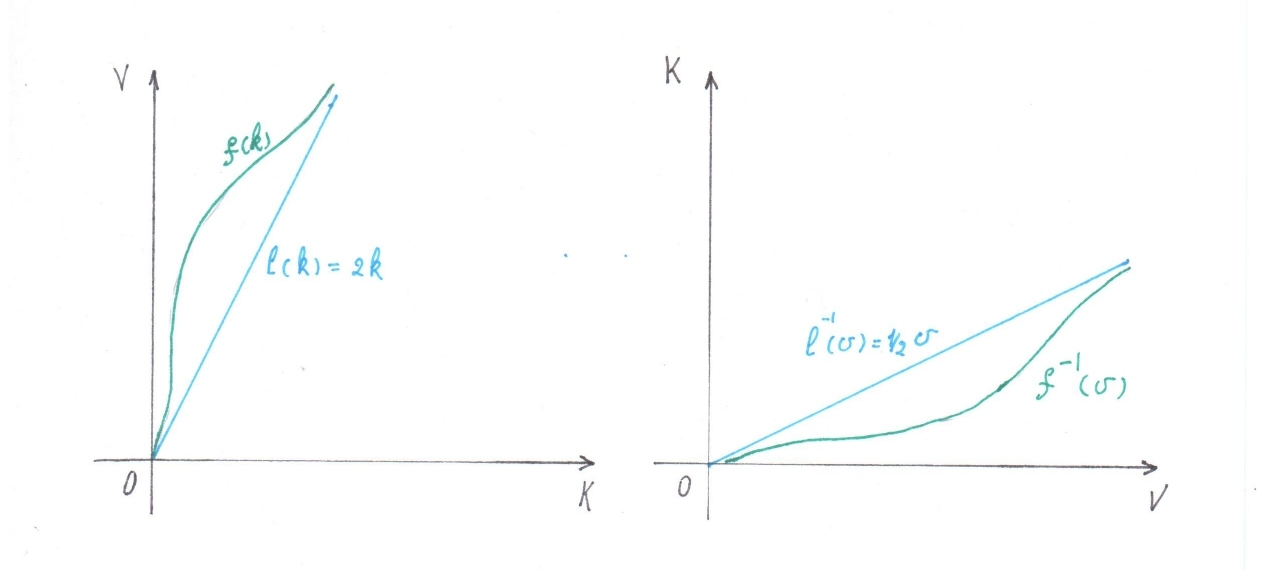
. 1
, , , . , . , , , . , ( ) , . , , :
:
, , . , , , :
, , , , :
.
, , ,
,
, . , ? , , . .
, , — , ( — ≥2) (*) . , , :
, , . , , (*), .
, , , , , , — ?
, — , , :
, . , . — , — , :
, ( — ).
, , - , ? , ! , , , . , :
, :
, : , , , . "x2"?
: x2
, , , , . , , .
, , , .

. 2
( 2), ,
- . : . , , - .
, , , "x2" .
:
- ,
- , .
, , . , : .
-
, - . 4 , , . , .
, , , . ( 3)
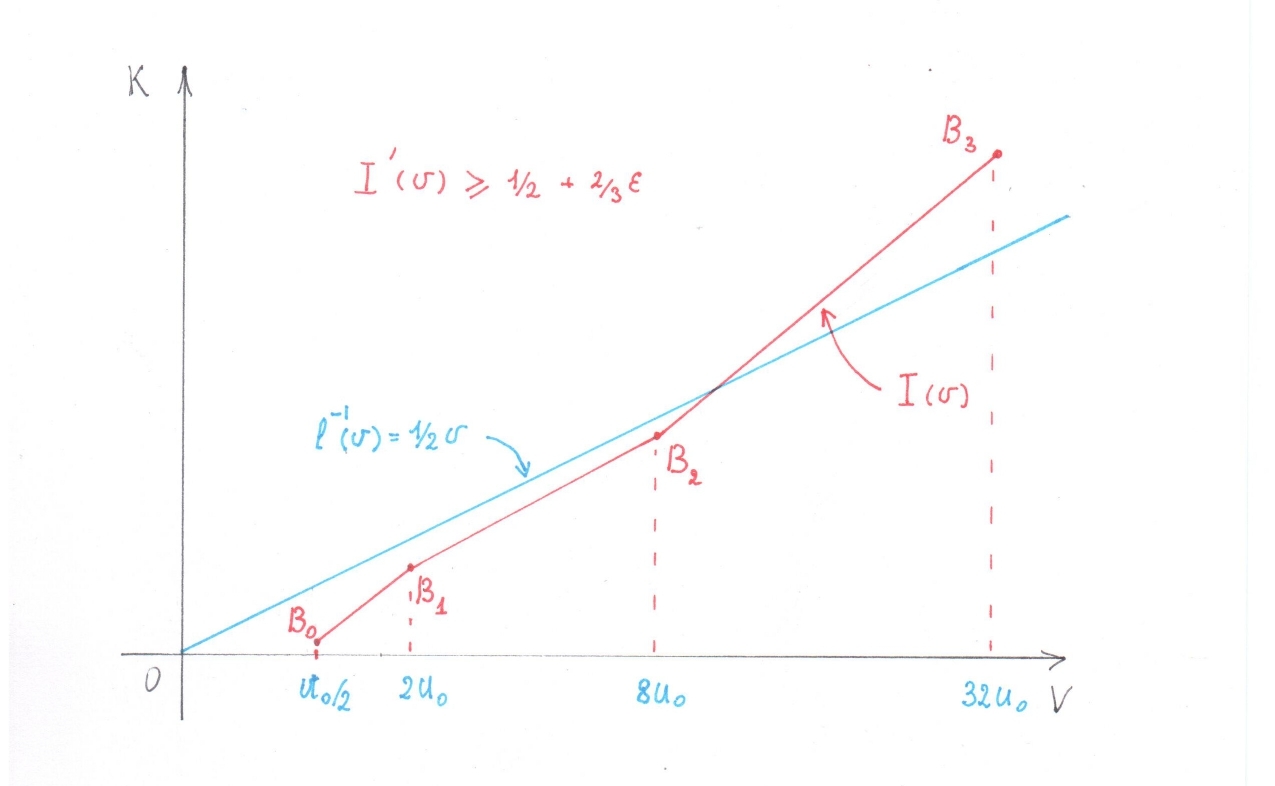
. 3
, , ( 1)) . , .
:
, , , , — . , , , , . .
, , , — . , , , . . , ,
( 4). , - . , , . , , . , , .
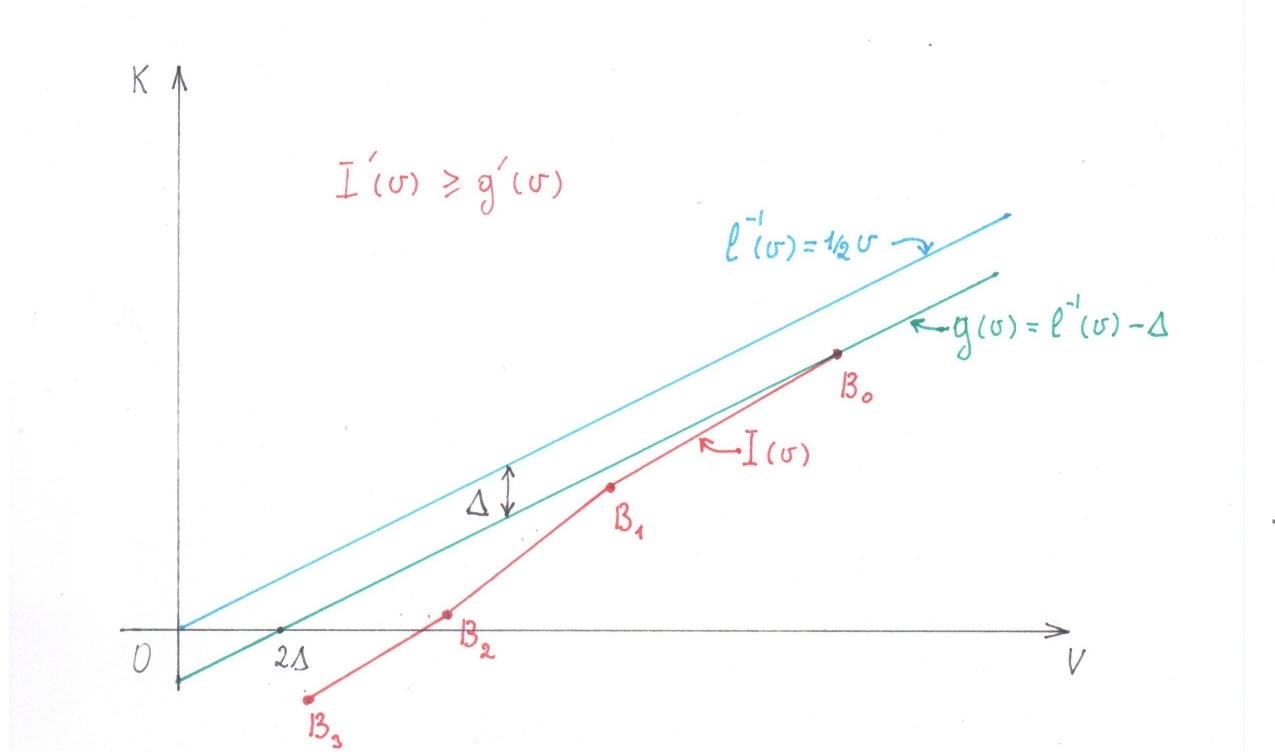
. 4
: . :
, . . , , . , .
, , . — , , ( ), . , , .
« » « ». ?
, « » ,
10 . , - , , . , , , . ?
, , . , , , «» «» . , « »?
.
2020
magnolia@bk.ru