Python and set theory

Python has a very useful datatype for working with sets - set . This data type, examples of use, and a small excerpt from set theory will be discussed later.

A reservation should be made right away that this article in no way pretends to any mathematical rigor and completeness, rather, it is an attempt to demonstrate in an accessible way examples of using sets in the Python programming language.

– , , , - , . :

– .

? , , .

, . , , .

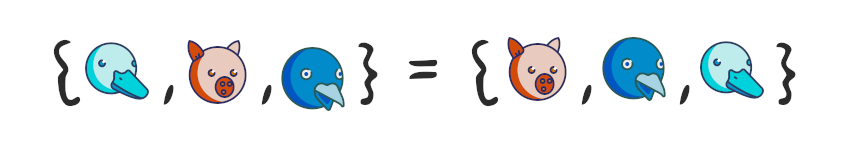
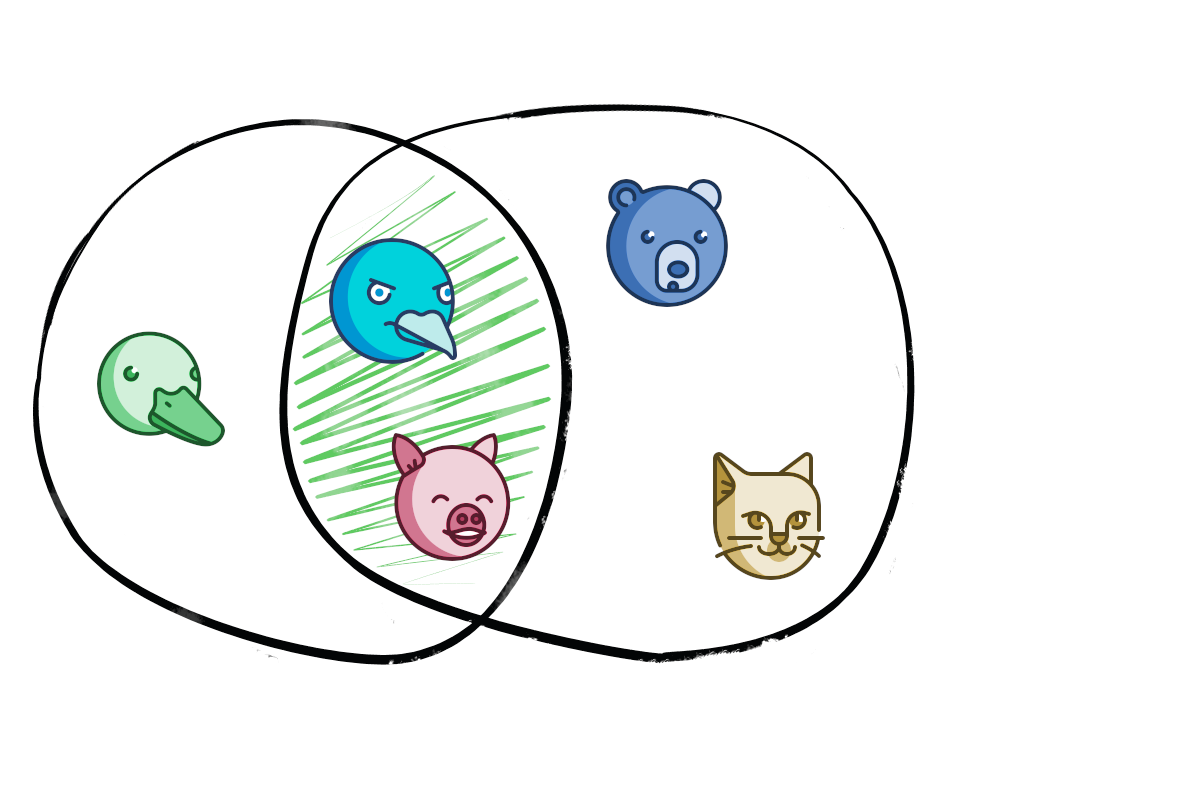
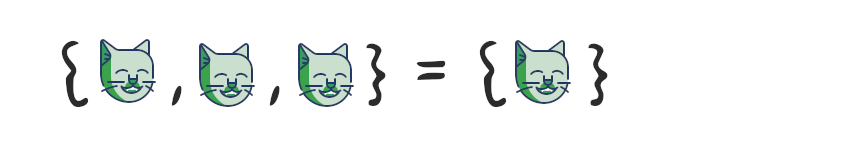
, , , – . , , . Python, .

Python

Python . – :

fruits = {"banana", "apple", "orange"}

, . :

wrong_empty_set = {}
print(type(wrong_empty_set))

# 
<class "dict">

set():

correct_empty_set = set()
print(type(correct_empty_set))

# 
<class "set">

set() - , (Iterable):

color_list = ["red", "green", "green", "blue", "purple", "purple"]
color_set = set(color_list)
print(color_set)

#  (   ):
{"red", "purple", "blue", "green"}

– set comprehension. , list comprehension ( ).

numbers = [1, 2, 2, 2, 3, 3, 4, 4, 5, 6]

#      - 
#     
even_numbers = {
    number for number in numbers
    if number % 2 == 0
}
print(even_numbers)

#  (   ):
{2, 4, 6}

, ( ) Python (Hashable) . , set -. , – , . Python (int, float, str, bool, ..) – . , tuple, , .

#   (tuple)
records = {
    ("", 17_200_000), 
    ("-", 5_400_000), 
    ("", 1_600_000),
    ("", 17_200_000),
}

for city, population in records:
    print(city)

#  (   ):


-

. - , , .. "" .

class City:
    def __init__(self, name: str):
        self.name = name

    def __repr__(self) -> str:
        """   __repr__    
        """
        return f'City("{self.name}")'

print(City("Moscow") == City("Moscow"))

# :
False

cities = {City("Moscow"), City("Moscow")}
print(cities)

# 
{City("Moscow"), City("Moscow")}

, City("Moscow") , cities .

, City:

class City:
    def __init__(self, name: str):
        #  name   ,   
        #       
        self._name = name

    def __hash__(self) -> int:
        """   
        """
        return hash((self._name, self.__class__))

    def __eq__(self, other) -> bool:
        """    ( ==)
        """
        if not isinstance(other, self.__class__):
            return False
        return self._name == other._name

    def __repr__(self) -> str:
        """   __repr__    
        """
        return f'City("{self._name}")'

, :

moscow = City("Moscow")
moscow_again = City("Moscow")

print(moscow == moscow_again and hash(moscow) == hash(moscow_again))
# :
True

#        
cities = {City("Moscow"), City("Kazan"), City("Moscow")}
print(cities)

#  (   ):
{City("Kazan"), City("Moscow")}

set Python Collection ( ), :

iterable-

- in. . O(1) , -.

tremendously_huge_set = {"red", "green", "blue"}

if "green" in tremendously_huge_set:
    print("Green is there!")
else:
    print("Unfortunately, there is no green...")

# :
Green is there!

if "purple" in tremendously_huge_set:
    print("Purple is there!")
else:
    print("Unfortunately, there is no purple...")

# :
Unfortunately, there is no purple...

– , . .

even_numbers = {i for i in range(100) if i % 2 == 0}

#  
cardinality = len(even_numbers)
print(cardinality)

# :
50

, , , iterable-.

colors = {"red", "green", "blue"}

#        for
for color in colors:
    print(color)

#  (   ):
red
green
blue

#    ,   iterable-
color_counter = dict.fromkeys(colors, 1)
print(color_counter)

#  (   ):
{"green": 1, "red": 1, "blue": 1}

, . .

– , . , .

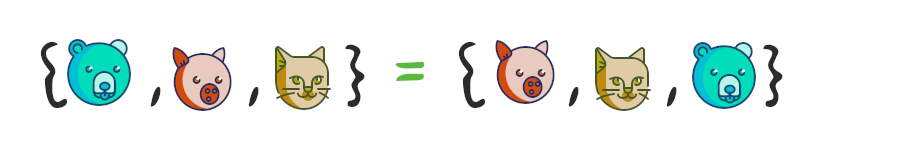
my_fruits = {"banana", "apple", "orange", "orange"}
your_fruits = {"apple", "apple", "banana", "orange", "orange"}
print(my_fruits == your_fruits)

# :
True

, , . , .

even_numbers = {i for i in range(10) if i % 2 == 0}
odd_numbers = {i for i in range(10) if i % 2 == 1}

# ,        
if even_numbers.isdisjoint(odd_numbers):
    print("  !")

# :
  !

S – , S. S .

#     100
fibonacci_numbers = {0, 1, 2, 3, 34, 5, 8, 13, 21, 55, 89}

#     100
natural_numbers = set(range(100))

#       
#  
if fibonacci_numbers.issubset(natural_numbers):
    print("!")

# :
!

#       
#    
if natural_numbers.issuperset(fibonacci_numbers):
    print("!")

# :
!

empty = set()

#  issubset  issuperset    iterable-
print(
    empty.issubset(range(100))
    and empty.issubset(["red", "green", "blue"])
    and empty.issubset(set())
)

# :
True

natural_numbers = set(range(100))

if natural_numbers.issubset(natural_numbers):
    print("!")

# :
!

, .

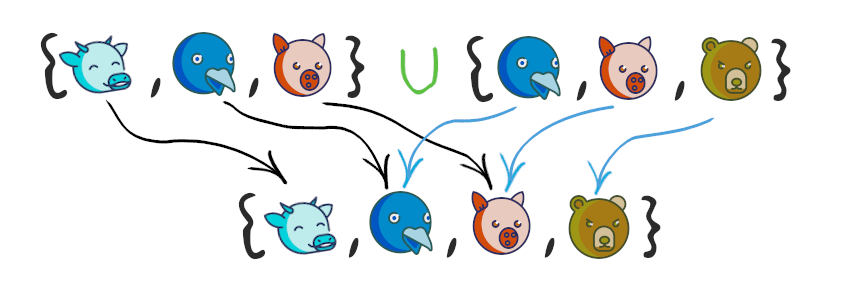
– , . Python , .

my_fruits = {"apple", "orange"}
your_fruits = {"orange", "banana", "pear"}

#       `|`,
#       set
our_fruits = my_fruits | your_fruits
print(our_fruits)

#  (   ):
{"apple", "banana", "orange", "pear"}

#     union.
#    ,   union   
#   set,   iterable-
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)

#  (   ):
{"apple", "banana", "orange", "pear"}

, , . O(1).

colors = {"red", "green", "blue"}

#  add     
colors.add("purple")
#  ,     ,  
#  
colors.add("red")
print(colors)

#  (   ):
{"red", "green", "blue", "purple"}

#  update  iterable- (, ,   ..)
#      
numbers = {1, 2, 3}
numbers.update(i**2 for i in [1, 2, 3])
print(numbers)

#  (   ):
{1, 2, 3, 4, 9}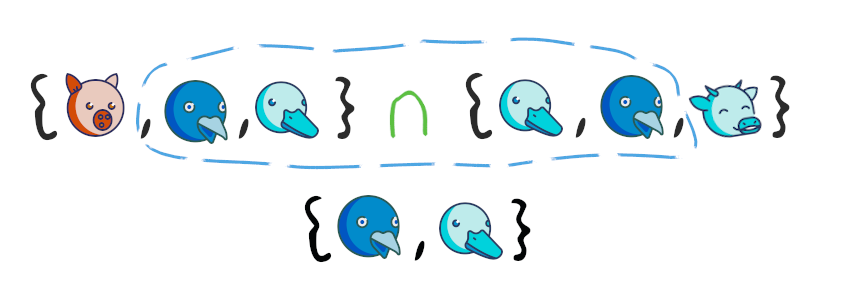

– , , .

def is_prime(number: int) -> bool:
    """  True,  number -   
    """
    assert number > 1
    return all(number % i for i in range(2, int(number**0.5) + 1))

def is_fibonacci(number: int) -> bool:
    """  True,  number -   
    """
    assert number > 1
    a, b = 0, 1
    while a + b < number:
        a, b = b, a + b
    return a + b == number

#     100
primes = set(filter(is_prime, range(2, 101)))

#     100
fibonacci = set(filter(is_fibonacci, range(2, 101)))

#     100,   
#  
prime_fibonacci = primes.intersection(fibonacci)

#    `&`,    
prime_fibonacci = fibonacci & primes

print(prime_fibonacci)

#  (   ):
{2, 3, 5, 13, 89}

& , set. intersection, , iterable-. , , intersection_update, intersection, -.

– , , .

i_know: set = {"Python", "Go", "Java"}
you_know: dict = {
    "Go": 0.4, 
    "C++": 0.6, 
    "Rust": 0.2, 
    "Java": 0.9
}

#  ,   `-`  
#    set
you_know_but_i_dont = set(you_know) - i_know
print(you_know_but_i_dont)

#  (   ):
{"Rust", "C++"}

#  difference     iterable-,
#   dict, 
i_know_but_you_dont = i_know.difference(you_know)
print(i_know_but_you_dont)

# :
{"Python"}

, – . , , , . O(1).

fruits = {"apple", "orange", "banana"}

#    .   
#   ,    
fruits.discard("orange")
fruits.discard("pineapple")
print(fruits)

#  (   ):
{"apple", "banana"}

#  remove   discard,   ,
#      
fruits.remove("pineapple")  # KeyError: "pineapple"

differene_update, iterable- iterable-. difference, , .

numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
even_numbers_under_100 = (i for i in range(1, 101) if i % 2 == 0)
numbers.difference_update(even_numbers_under_100)
print(numbers)

#  (   ):
{1, 3, 5, 7, 9}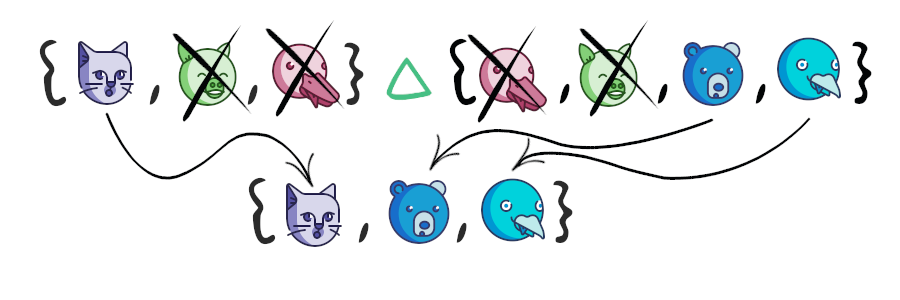

– , , . .

non_positive = {-3, -2, -1, 0}
non_negative = {0, 1, 2, 3}

#  ,   `^`  
#     set
non_zero = non_positive ^ non_negative
print(non_zero)

#  (   ):
{-1, -2, -3, 1, 2, 3}

, 0 , . , ^, – symmetric_difference symmetric_difference_update. iterable- , , symmetric_difference -, symmetric_difference_update .

non_positive = {-3, -2, -1, 0}
non_negative = range(4)

non_zero = non_positive.symmetric_difference(non_negative)
print(non_zero)

#  (   ):
{-1, -2, -3, 1, 2, 3}

#  symmetric_difference_update   
colors = {"red", "green", "blue"}
colors.symmetric_difference_update(["green", "blue", "yellow"])
print(colors)

#  (   ):
{"red", "yellow"}

Conclusion

I hope I've been able to show that Python has very nice built-in tools for working with sets. In practice, this often allows you to reduce the amount of code, make it more expressive and easier to understand, and therefore more maintainable. I will be glad if you have any constructive comments and additions.

useful links

Sets (Wikipedia article)

Type documentation for set

Iterables (Python Glossary)

Hashable objects (Python Glossary)

Sets in Python

Set Theory: the Method To Database Madness

Python and set theory

Python and set theory

Python

Conclusion

useful links

More articles: