
"Blade Runner", "Air Prison", "Heavy Rain" - what do these representatives of mass culture have in common? In all, to one degree or another, there is an ancient Japanese art of paper folding - origami. In movies, games and in real life, origami is often used as a symbol of certain feelings, some kind of memories or a kind of message. It is rather an emotional component of origami, but from the point of view of science, many interesting aspects from a variety of directions are hidden in paper figures: geometry, mathematics and even mechanics. Today we take a look at a study in which scientists from the American Institute of Physics created a data storage device by folding / unfolding origami figures. How exactly does a paper memory card work,what principles are implemented in it and how much data can such a device store? We will find answers to these questions in the report of scientists. Go.
It is difficult to say exactly when origami appeared. But we know for sure that no earlier than 105 A.D. It was in this year in China that Tsai Lun invented paper. Of course, up to this point, paper already existed, but it was not made of wood, but of bamboo or silk. The first option was not easy, and the second was extremely expensive. Tsai Long was commissioned to come up with a new recipe for paper that would be light, cheap, and easy to make. Not an easy task, but Tsai Lun turned to the most popular source of inspiration - nature. For a long time he observed wasps, whose dwellings were made of wood and plant fibers. Tsai Lun conducted many experiments in which he used a variety of materials for future paper (tree bark, ash and even fishing nets) mixed with water.The resulting mass was laid out in a special form and dried in the sun. The result of this colossal work was a prosaic subject for a modern person - paper.

In 2001, a park named after Tsai Lun was opened in Leiyang, China.
The spread of paper to other countries did not happen instantly, only at the beginning of the 7th century its recipe reached Korea and Japan, and paper reached Europe only in the 11th-12th century.
The most obvious uses for paper are, of course, in both manuscripts and printing. However, the Japanese found a more elegant application for it - origami, i.e. folding paper figures.
A short excursion into the world of origami and engineering.
There are a great many origami options, as well as the techniques for making them: simple origami, kusudama (modular), wet folding, pattern origami, kirigami, etc. (The Essential Guide to Origami )
From the point of view of the science, origami is a mechanical metamaterial whose properties are determined by its geometry, not the properties of the material from which it is made. It has been demonstrated for quite some time that versatile 3D deployable structures with unique properties can be created using repetitive origami patterns.
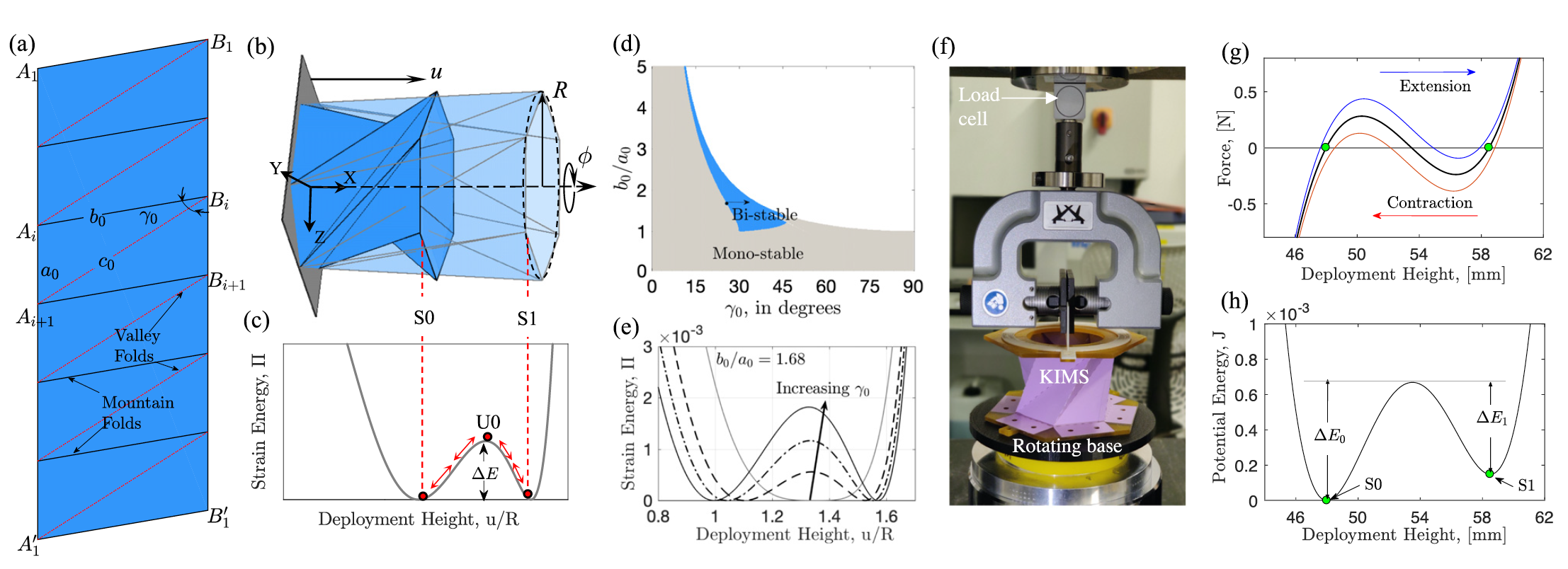
Image No. 1
In image 1ban example of such a structure is shown - a deployable bellows, built from one sheet of paper according to the scheme in 1a . From the available origami options, scientists have identified an option that implements a mosaic of identical triangular panels arranged in a cyclic symmetry, known as the origami of Cresling.
It is important to note that origami-based structures are of two types: rigid and non-rigid.
Rigid origami are three-dimensional structures in which only the folds between the panels are deformed during unfolding.
A prime example of hard origami is Miura-ori, used to create mechanical metamaterials with negative Poisson's ratio. This material has a wide range of applications: space exploration, deformable electronics, artificial muscles and, of course, reprogrammed mechanical metamaterials.
Non-rigid origami are three-dimensional structures that exhibit non-rigid elastic deformation of panels between folds during deployment.
An example of such an origami variation is the previously mentioned Cresling pattern, which has been used successfully to create structures with customizable multistability, stiffness, deformation, softening / hardening, and / or nearly zero stiffness.
Research results
Inspired by the ancient art, scientists decided to use Kresling's origami to develop a cluster of mechanical binary switches that can be forced to switch between two different static states using a single controlled input in the form of harmonic excitation applied to the base of the switch.
As seen in 1b , the bellows is secured at one end and is subjected to an external load in the x direction at the other free end. Due to this, it undergoes simultaneous deflection and rotation along and around the x-axis. The energy accumulated during the deformation of the bellows is released when the external load is removed, causing the bellows to return to its original shape.
Simply put, we see a torsional torsion spring, the restoring ability of which depends on the shape of the function of the potential energy of the bellows. This, in turn, depends on the geometric parameters (a 0 , b 0 , γ 0 ) of the composite triangle used to build the bellows, as well as the total number (n) of these triangles ( 1a ).
For a certain combination of geometric parameters of the structure, the potential energy function of the bellows has a single minimum corresponding to one stable equilibrium point. For other combinations, the potential energy function has two minima, corresponding to two stable static bellows configurations, each associated with a different equilibrium height or, alternatively, spring deflection ( 1c ). This type of spring is often called bistable (video below).
Image 1d shows the geometric parameters leading to the formation of a bistable spring and the parameters leading to the formation of a monostable spring for n = 12.
The bistable spring can stop in one of its equilibrium positions in the absence of external loads and can be activated to switch between them when the proper amount of energy is available. It is this property that is the basis of this study, which explores the creation of Kresling-inspired mechanical switches (KIMS ) with two binary states.
In particular, as shown in 1c, the switch can be activated to transition between its two states by supplying enough energy to overcome the potential barrier (∆E). Energy can be supplied as a slow quasi-static actuation or by applying a harmonic signal to the base of the switch with an excitation frequency close to the local resonance frequency of the switch in its various equilibrium states. In this study, it was decided to use the second option, since the harmonic resonant response in some parameters is superior to the quasi-static one.
First, resonant actuation requires less switching effort and is generally faster. Second, resonant switching is insensitive to external disturbances that do not resonate with the switch in its local states. Third, since the potential switch function is usually asymmetric about the unstable equilibrium point U0, the harmonic excitation characteristics required to switch from S0 to S1 are usually different from those required to switch from S1 to S0, resulting in the possibility of excitation-selective binary switching. ...
This KIMS configuration is ideal for creating a multi-bit mechanical memory board using multiple binary switches with different characteristics on the same harmonically excited platform. The creation of such a device is due to the sensitivity of the form of the function of the potential energy of the switch to changes in the geometric parameters of the main panels ( 1e ).
Consequently, several KIMS with different design characteristics can be placed on the same platform and excited to transition from one state to another, individually or in combination using different sets of excitation parameters.
During the practical test, a switch was created from paper with a density of 180 g / m 2.with geometric parameters: γ 0 = 26.5 °; b 0 / a 0 = 1.68; a 0 = 40 mm and n = 12. It is these parameters, judging by the calculations ( 1d ), and lead to the fact that the resulting spring will be bistable. The calculations were carried out using a simplified model of the axial truss (structure of rods) of the bellows.
Using a laser, perforated lines ( 1a ) were made on a sheet of paper , which are the folding places. Then folds were made along the edges b 0 (outward curved) and γ 0 (inward curved), and the distal ends were tightly connected. The top and bottom surfaces of the switch have been reinforced with acrylic polygons.
The restoring force curve of the switch was obtained experimentally through compression and tension tests carried out on a universal testing machine with a special setup that allows the base to be rotated during tests ( 1f ).
The ends of the acrylic switch polygon were rigidly fixed, and a controlled displacement was applied to the top polygon at a predetermined rate of 0.1 mm / s. Tensile and compressive displacements were applied cyclically and limited to 13 mm. Immediately prior to the actual testing of the device, the breaker is configured by performing ten such load cycles before the restoring force is recorded by the 50N load cell. At 1gshows the curve of the restoring force of the switch obtained experimentally.
Then, by integrating the average restoring force of the switch over the operating range, the potential energy function ( 1h ) was calculated . The minima in the potential energy function are static equilibria associated with two switch states (S0 and S1). For this particular configuration, S0 and S1 occur at deployment heights u = 48 mm and 58.5 mm, respectively. The potential energy function is clearly asymmetric with different energy barriers ∆E 0 at point S0 and ∆E 1 at point S1.
The switches were placed on an electrodynamic shaker that provides controlled excitation of the base in the axial direction. In response to the excitation, the top surface of the switch oscillates vertically. The position of the upper surface of the switch relative to the base was measured with a laser vibrometer ( 2a ).
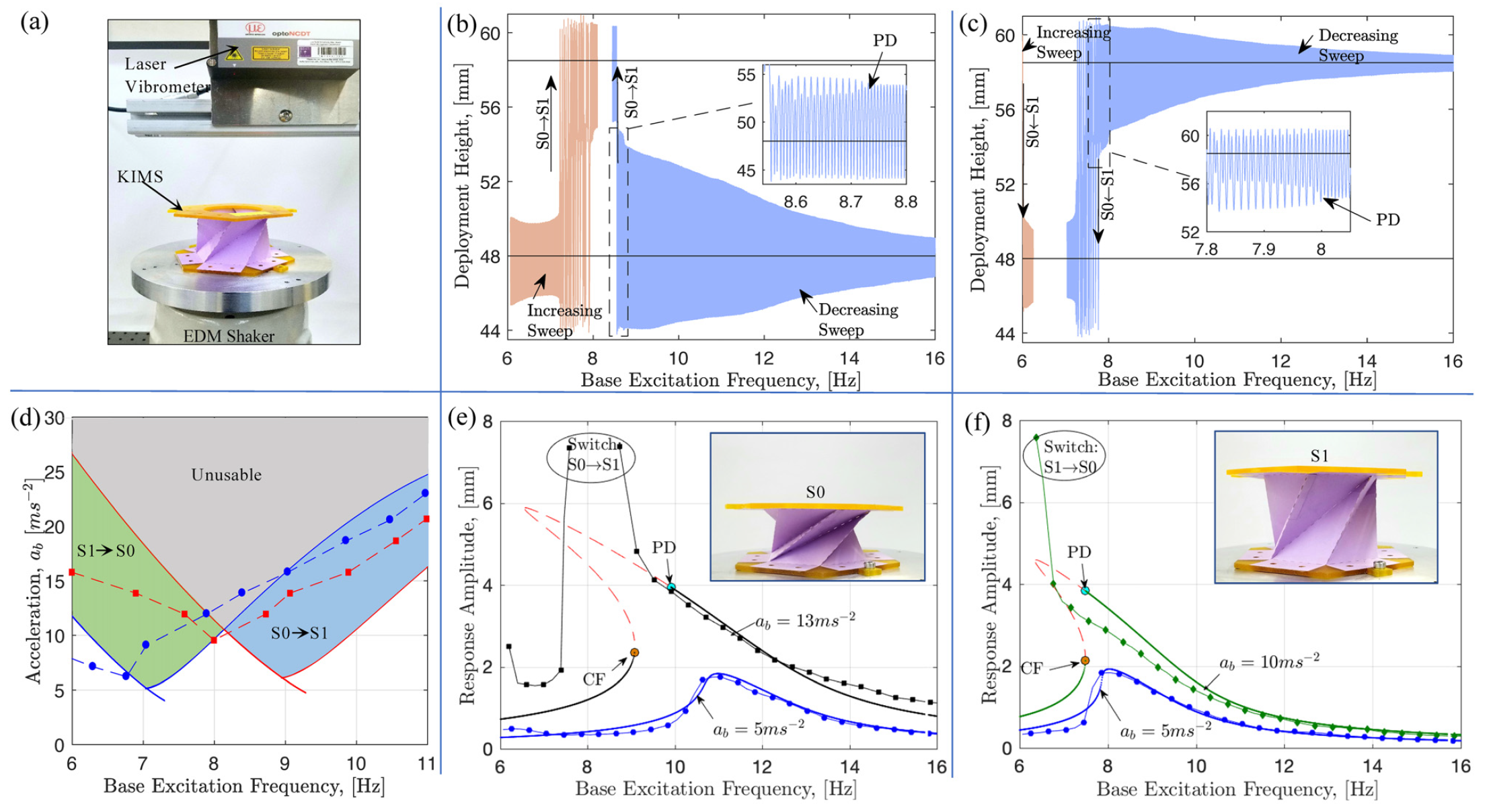
Image # 2
It was found that the local resonant frequency of the switch for its two states is 11.8 Hz for S0 and 9.7 Hz for S1. To initiate the transition between the two states, that is, exit from the potential well * , a very slow (0.05 Hz / s) bidirectional linear frequency sweep was carried out around the identified frequencies with a base acceleration of 13 ms -2... Specifically, KIMS was initially located at S0, and the incremental frequency sweep was initiated at 6 Hz.
Potential well * - an area where there is a local minimum of the potential energy of a particle.As can be seen in 2b , when the drive frequency reaches about 7.8 Hz, the switch exits the S0 potential well and enters the S1 potential well. The switch continued to remain at S1 as the frequency increased further.
The switch was then set to S0 again, but this time a downward sweep was initiated at 16 Hz. In this case, when the frequency approaches 8.8 Hz, the switch exits S0 and enters and remains in potential well S1.
The S0 state has an activation band of 1 Hz [7.8, 8.8] with an acceleration of 13 ms -2 , and S1 - 6 ... 7.7 Hz ( 2s ). It follows from this that KIMS can selectively switch between the two states due to harmonic excitation of the base of the same magnitude, but different frequency.
The KIMS switching bandwidth has a complex dependence on the shape of its potential energy function, damping characteristics and harmonic excitation parameters (frequency and magnitude). In addition, due to the softening non-linear behavior of the switch, the activation bandwidth does not necessarily include the linear resonant frequency. Thus, it is important that a switch activation map is created for each KIMS individually. This map is used to characterize the frequency and magnitude of the excitation, which results in switching from one state to another and vice versa.
Such a map can be created experimentally by frequency sweeping at different levels of excitation, but this process is very laborious. Therefore, the scientists decided at this stage to proceed to modeling the switch using the potential energy function determined during the experiments ( 1h ).
The model assumes that the dynamic behavior of the switch can be well approximated by the dynamics of an asymmetric bistable Helmholtz – Duffing oscillator, the equation of motion of which can be expressed as follows:
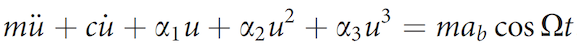
where u is the deviation of the moving edge of the acrylic polygon relative to the fixed one; m is the effective mass of the switch; c - coefficient of viscous damping, determined experimentally; ai s - bistable coefficients of the restoring force; a b and Ω - base value and acceleration frequency.
The main task of modeling is to use this formula to establish combinations of a b and Ω, which allow switching between two different states.
Scientists note that the critical excitation frequencies at which a bistable oscillator transitions from one state to another can be approximated by two bifurcation frequencies * : period doubling bifurcation (PD) and cyclic fold bifurcation (CF).
Bifurcation * - a qualitative change in the system by changing the parameters on which it depends.Using the approximation, the frequency response curves of the KIMS were plotted in two of its states. Graph 2e shows the frequency response curves of the switch at S0 for two different baseline acceleration levels.
At a baseline acceleration of 5ms -2 , the AFC curve shows slight softening, but no instability or bifurcations. Thus, the switch remains in the S0 state, no matter how the frequency changes.
However, when the base acceleration is increased to 13 ms -2 , the stability decreases due to the PD bifurcation as the drive frequency decreases.
In the same way, the frequency response curves of the switch in S1 ( 2f ) were obtained . At 5ms acceleration-2 the observed picture remains the same. However, as the base acceleration increases to 10 ms -2 , PD and CF bifurcations appear. Excitation of the switch at any frequency between these two bifurcations results in a switch from S1 to S0.
Simulation data suggests that there are vast areas in the activation map in which each state can be activated in a unique way. This allows selective switching between the two states depending on the frequency and magnitude of the trigger. You can also see that there is an area where both states can toggle at the same time.

Image No. 3
A combination of several KIMS can be used to create a mechanical memory of several bits. By varying the geometry of the switch so that the shape of the potential energy function of any two switches is sufficiently different, the activation bandwidth of the switches can be designed so that they do not overlap. As a result, each switch will have unique drive parameters.
To demonstrate this technique, a 2-bit board was created on the basis of two switches with different potential characteristics ( 3a ): bit 1 - γ 0 = 28 °; b 0 / a 0 = 1.5; a 0 = 40 mm and n = 12; bit 2 - γ 0 = 27 °; b 0 / a 0= 1.7; a 0 = 40 mm and n = 12.
Since each bit has two states, a total of four different states S00, S01, S10 and S11 ( 3b ) can be achieved . The numbers after S indicate the value of the left (bit 1) and right (bit 2) switches.
The behavior of a 2-bit switch is shown in the video below:
On the basis of this device, you can also create a cluster of switches, which can be the basis of multi-bit mechanical memory cards.
For a more detailed acquaintance with the nuances of the study, I recommend that you look into the report of scientists and additional materials to it.
Epilogue
Hardly any of the creators of origami could have imagined how their creation would be used in the modern world. On the one hand, this speaks of a large number of complex elements hidden in ordinary paper figures; on the other, that modern science is able to use these elements to create something completely new.
In this work, scientists were able to use the geometry of Cresling's origami to create a simple mechanical switch capable of being in two different states, depending on the input parameters. This can be compared to 0 and 1, which are the classic units of information.
The resulting devices were combined into a mechanical memory system capable of storing 2 bits. Knowing that one letter occupies 8 bits (1 byte), the question arises - how many similar origami will be needed to write "War and Peace", for example.
Scientists are well aware of the skepticism that their development can generate. However, according to their own words, this research is an exploration in the field of mechanical memory. In addition, the origami used in the experiments should not be large; their dimensions can be significantly reduced without deteriorating their properties.
Be that as it may, this work cannot be called ordinary, trivial or boring. Science is not always used to develop something specific, and scientists do not always initially know what they are creating. After all, most inventions and discoveries were the result of a simple question - what if?
Thanks for your attention, stay curious and have a great weekend, guys! :)
A bit of advertising
Thank you for staying with us. Do you like our articles? Want to see more interesting content? Support us by placing an order or recommending to friends, cloud VPS for developers from $ 4.99 , a unique analogue of entry-level servers that we have invented for you: The Whole Truth About VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps from $ 19 or how to divide the server correctly? (options available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).
Is Dell R730xd 2x cheaper in Equinix Tier IV data center in Amsterdam? Only we have 2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 TV from $ 199 in the Netherlands!Dell R420 - 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB - From $ 99! Read about How to build the infrastructure of bldg. class with Dell R730xd E5-2650 v4 servers at a cost of 9000 euros for a penny?