Physicists have found the algebraic structure underlying the intricate mathematics of particle collisions. Some hope it will lead us to a more elegant theory of the physical world.
When particle physicists try to model experiments, they are confronted with impossible calculations due to an infinitely large equation that is beyond the reach of modern mathematics.
Fortunately, they can make generally accurate predictions without working through all this cryptic mathematics to the end. Shortening the calculations, scientists at the Large Hadron Collider at CERN, Europe, make predictions that coincide with the events they then observe in collisions of subatomic particles sweeping at a tremendous speed along a 26-kilometer track.
Unfortunately, the era of agreement between prediction and observation may be coming to an end. The more accurate measurements become, the more difficult it is for the approximate computation schemes used by theorists to keep up.
“We are already close to exhausting the funds we have,” said Claude Dar , a particle physicist at CERN.
However, three recent works by Pierpaolo Mastrolia of the University of Padua in Italy and Sebastian Mizerafrom the Princeton Institute for Advanced Study in New Jersey discovered the mathematical structure underlying these equations. It provides a new way of collapsing an infinite number of members to a dozen required components. Their method can help take prediction accuracy to the next level that theorists need to go beyond the leading but incomplete model of particle physics.
“They have shown many results proving the viability of this promising technique,” said Dar.
However, the benefits can be far greater than simply improving predictions. The new method bypasses the traditional dreary math by directly calculating "intersection numbers", which some believe may ultimately give us a more elegant description of the subatomic world.
“It's not just mathematics,” said Simon Caron-Hewot of McGill University, a quantum theorist who studies the implications of Mastrolius and Mizera's work. "It's all very deeply intertwined with quantum field theory."
Infinite loop
When simulating particle collisions, physicists use Feynman diagrams , a simple notation invented by Richard Feynman in the 1940s.
To understand how this recording works, consider a simple event: two quarks approach each other, exchange one gluon in the process of "collision," and then bounce off each other along different trajectories.
In the Feynman diagram, quark paths are indicated by “legs”, which form “tops” at the junction during particle interaction. Feynman developed rules for turning such a picture into equations that calculate the probability of this event occurring. You write a specific function for each leg and vertex - usually a fraction using the particle's mass and momentum - and multiply it all. For simple options like ours, the calculations might fit on a napkin.
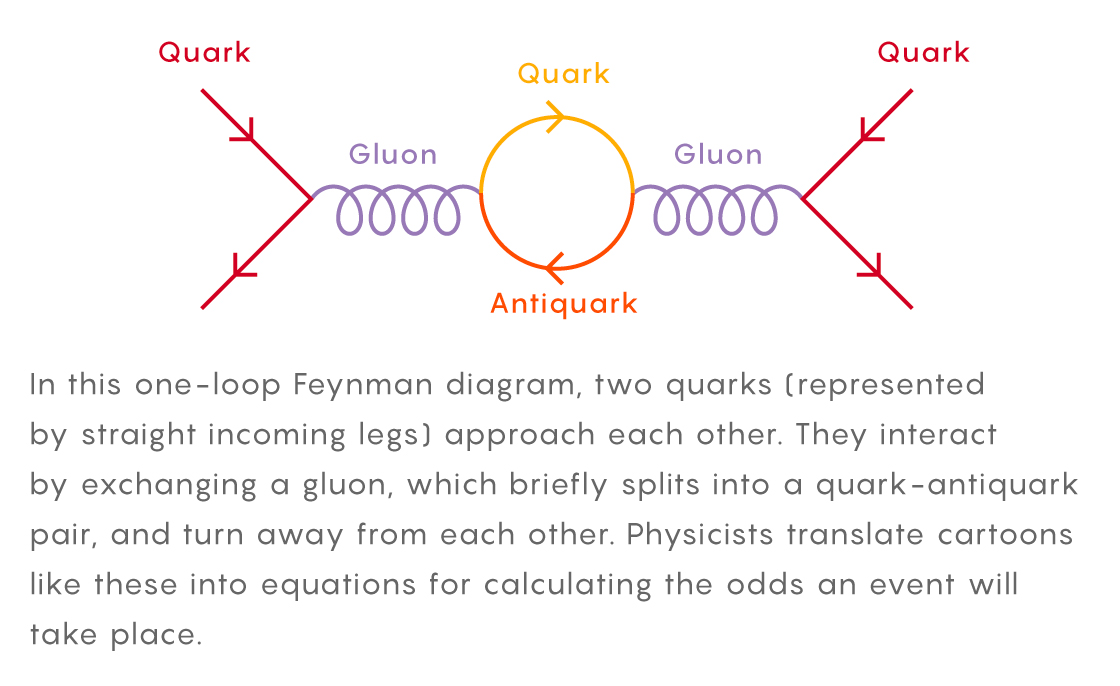
In this diagram, two quarks (indicated by straight legs with arrows pointing inward) approach one loop. They interact, exchanging gluons, which for a short period of time splits into a quark-antiquark pair, and then fly apart. Physicists translate these patterns into equations that calculate the probability of this event occurring.
However, the golden rule of quantum theory is to consider all possibilities, and the exchange of a simple gluon is just one of the vast variety of scenarios that can unfold when two quarks collide. The gluon that the particles exchange can split into a quark-antiquark pair for a short period of time, and then turn back into a gluon. Two quarks meet and two quarks diverge, but a lot can happen in between. To fully account for what is happening, giving an ideal prediction, you will need to draw an infinite number of diagrams. Nobody expects perfect results, but the key to improving the accuracy of calculations is to go as far as possible along the endless chain of events.
And this is where physicists get stuck.
To study this hidden center in more detail, you need to turn to virtual particles - quantum fluctuations that gradually affect the result of each interaction. The short-term existence of the pair of quarks mentioned above, like many virtual events, is indicated on the Feynman diagram by a closed loop. Loops baffle physicists - they are black boxes that add extra layers to endless scenarios. In order to somehow calculate the possibilities implied by the loop, theorists need to take integrals. These integrals reach monstrous proportions in Feynman diagrams with many loops that appear as researchers move further down the chain of events and account for increasingly complex virtual interactions.
Physicists have algorithms for calculating the probabilities of scenarios without loops or with one loop, but already collisions with two loops bring computers to their knees. This is the ceiling for predictive accuracy - and for physicists to understand the implications of quantum theory.
However, all this has one positive side: physicists do not need to calculate absolutely all the integrals of a complex Feynman diagram, since most of them can be collected into one.
Thousands of integrals can be reduced to several dozen "basic" ones, which can be weighted and added. But what integrals can be collected into separate basic ones is a difficult computational question. Researchers use computers that essentially make guesses based on millions of interactions and have difficulty deriving meaningful combinations of integrals.
However, thanks to the intersection numbers, physicists may have found a way to elegantly select important information from sprawling calculations of Feynman integrals.
Geometric fingerprint
The work of Mastrolia and Mizera grows out of such an offshoot of mathematics as algebraic topology , which classifies forms and spaces. Help in this theories of " cohomology ", allowing you to calculate algebraic "fingerprints" from complex geometric spaces.
"It's kind of like a synopsis, an algebraic device that captures the essence of the space you're exploring," said Clement Dupont, a mathematician at the University of Montpellier in France.
Feynman diagrams can be translated into geometric spaces, which can then be analyzed using cohomology. Each point in such space can represent one of the many scenarios that unfold when particles collide.
We might hope that by taking the cohomology of this space — finding its algebraic structure — you could calculate the weights for the fundamental integrals. However, the geometric space that characterizes most Feynman diagrams is so curved that it resists a lot of cohomological computations.
In 2017, Mizera was trying to analyze object collisions in string theory when he stumbled upon the instruments first invented by Israel Gelfand and Katsuhiko Aomoto in the 1970s and 1980s when they were working on cohomology called twisted cohomology. Later that same year, Mizera met Mastrolia, who realized that these techniques could work on the Feynman diagram as well. Last year, they published three papers that used cohomology theory to speed up computations of simple particle collisions.
Their method takes a family of interconnected physical scenarios, presents it as geometric space, and calculates its twisted cohomology. “And this twisted cohomology tells everything about the integrals of interest to us,” said Mizera.
In particular, the twisted cohomology tells how many basic integrals are required and what their weights should be. These weights appear as values that they call "intersection numbers." As a result, thousands of integrals dry up to a weighted sum of several dozen basic ones.
It is possible that cohomology theories that produce these intersection numbers can do more than make the computation easier — they can point us to the physical significance of the most important quantities in computation.
For example, when a virtual gluon decays into two virtual quarks, their lifetimes can be different. In the geometrical space associated with them, each point can denote a different quark lifetime. When calculating the weights, the researchers see that scenarios with the longest-lived virtual particles - that is, those cases in which the particles become almost real - influence the result more than others.
“That's what's amazing about this method,” said Karon-Hewot. "He recreates everything from these rare, special events."
Last week Mizera, Mastrolia and their colleagues published another preprint, where it is shown that this technique has evolved enough to work with real diagrams with two loops. In the next work, Karon-Hewot will develop this method even further, possibly taming even three-loop diagrams.
If successful, this technique could help open up a new generation of theoretical predictions. And, as some researchers suspect, it may even show us a new perspective on reality.