Book “Programming Quantum Computers. Basic algorithms and code examples "

Hello Habitants! Quantum computers have sparked a new computer revolution, and you have a great chance to join the technological breakthrough right now. Developers, computer graphics specialists, and aspiring IT pros will find practical information on quantum computing that programmers need in this book. Instead of studying theory and formulas, you will immediately focus on specific problems that demonstrate the unique capabilities of quantum technology.



Eric Johnston, Nick Harrigan and Mercedes Gimeno-Segovia help develop the necessary skills and intuition, as well as master the tools needed to create quantum applications. You will understand what quantum computers are capable of and how to apply it in real life. The book consists of three parts: - Programming QPU: basic concepts of programming quantum processors, performing operations with qubits and quantum teleportation. - QPU primitives: algorithmic primitives and methods, amplitude amplification, quantum Fourier transform and phase estimation. - Practice QPU: solving specific problems using QPU primitives, quantum search methods and Shor's decomposition algorithm.

Real data

Complete QPU applications are built to work with real, non-training data. The real data is not always limited to the basic integers that we have gotten around to so far. Therefore, the question of how to represent more complex data in QPU is worth the effort, and good data structures can be just as important as good algorithms. In this chapter, we will try to answer two questions that have previously been bypassed:

1. How to represent complex data types in the QPU register? A positive integer can be represented in simple binary encoding. But what about irrational numbers, or even composite data types like vectors or matrices? This question takes on new depth when we consider that superposition and relative phase can provide new quantum coding options for these data types.
2. , QPU? , WRITE . , QPU . , , , QPU , .

Let's start with the first question. When describing QPU representations for data types of increasing complexity, we will come to the introduction of full-fledged quantum data structures and the concept of quantum random access memory (QRAM). Quantum RAM is a critical resource for many practical QPU applications.



The material in subsequent chapters will be highly dependent on the data structures presented in this chapter. For example, the so-called complex amplitude coding that will be described for vector data is central to all quantum machine learning applications introduced in Chapter 13.

Inappropriate data

How to encode non-integer numeric data in QPU register? The two standard ways to represent such values ​​in binary are fixed-point and floating-point representations. Although the floating point representation is more flexible (and adaptable to the range of values ​​that need to be represented with a certain number of bits), because of the high value of the qubits and our desire for simplicity, the fixed point representation is a better place to get started.



Fixed-point numbers are often described in Q-notation (unfortunately, Q in this case does not mean "quantum"). This helps to remove the ambiguity about where the fractional bits end and the integer bits begin. The Qn.m notation denotes an n-bit register, the m bits of which are for the fractional part (and therefore, the remaining (n - m) contain the integer part). Of course, you can use the same notation to specify how the QPU register should be used to encode a fixed point number. For example, in Fig. 9.1 shows an eight-qubit QPU register, which encodes the value 3.640625 in fixed-point representation Q8.6.



In the example given, the selected number can be accurately encoded in fixed point representation, because 3.640625 =Of course, such luck is not always found. Increasing the number of bits in the integer portion of a fixed-point register expands the range of integer values ​​that can be represented by it, while increasing the number of bits in the fractional portion improves the precision of the fractional portion of a number. The more qubits in the fractional part, the more likely it is that some combination 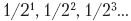can accurately represent a given number.





Although we will briefly mention the use of fixed-point representation in the following chapters, it plays an extremely important role in experimenting with real data in small QPU registers. When working with different encoding methods, you need to carefully monitor what specific encoding was used for data in a particular QPU register in order to correctly interpret the state of its qubits.

QRAM

QPU registers can store representations of different numeric values, but how do you store these values ​​in them? Hand-initialized data becomes outdated very quickly. What we really need is the ability to read values ​​from memory, fetching stored values ​​at a binary address. The programmer works with traditional random access memory using two registers: one is initialized with a memory address, and the other remains uninitialized. Random access memory writes to the second register the binary data stored at the address specified by the first register, as shown in Fig. 9.2.





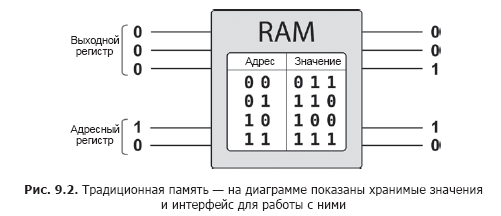
Can traditional memory be used to store the values ​​intended to initialize the QPU registers? Of course, the idea looks attractive.



If you want to initialize the QPU register with just one traditional value (two's complement, fixed-point, or simple binary encoding), then RAM is fine. The desired value is simply stored in memory, and write () and read () are used to write or read from the QPU register. It is this limited mechanism that has been used by the QCEngine JavaScript code to interact with QPU registers so far.



For example, the sample code in Listing 9.1, which receives an array a and implements the operation a [2] + = 1;, implicitly fetches this array of values ​​from RAM to initialize the QPU register. The circuit is shown in Fig. 9.3.

Sample code

This example can be done online at http://oreilly-qc.github.io?p=9-1.

Listing 9.1. Using QPU to increase the number in memory

var a = [4, 3, 5, 1];

qc.reset(3);
var qreg = qint.new(3, 'qreg');

qc.print(a);
increment(2, qreg);
qc.print(a);

function increment(index, qreg)
{
      qreg.write(a[index]);
      qreg.add(1);
      a[index] = qreg.read();
}

It is worth noting that in this simple case, not only the traditional RAM is used to store the integer, but also the traditional processor indexes the array to select and transmit the QPU of the desired value.



Although this use of RAM allows the QPU registers to be initialized to simple binary values, it has serious limitations. What if you need to initialize the QPU register with the superposition of stored values? For example, suppose that in RAM, the value 3 (110) is stored at address 0x01, and the value 5 (111) is stored at address 0x11. How do I prepare the input register in a superposition of these two values?



With traditional RAM and the clunky traditional write () operation, this will not work. Quantum processors, just like their tube ancestors once did, will need fundamentally new memory equipment - quantum in nature. Meet Quantum Random Access Memory (QRAM) lets you read and write data at the quantum level. There are already a few ideas on how to physically build QRAM, but it's worth noting that history may well repeat itself, and incredibly powerful quantum processors may appear long before there is any workable quantum memory hardware.



It is worth explaining a little more precisely what QRAM does. Like traditional memory, QRAM receives two registers as input: the QPU address register for the memory address and the QPU output register, which returns the value stored at the given address. For QRAM, both registers are composed of qubits. This means that in the address register it is possible to set a superposition of memory cells and, as a consequence, obtain a superposition of the corresponding values ​​in the output register (Fig. 9.4).





So QRAM actually allows you to read the stored values ​​in superposition. The exact complex amplitudes of the superposition to be obtained in the output register are determined by the superposition provided in the address register. In fig. Figure 9.2 shows the differences when performing the same increment operation in Listing 9.1 (Figure 9.5), but using QRAM to access the data instead of QPU read / write operations. The letter "A" denotes the register in which the QRAM address (or superposition) is transmitted. The letter "D" denotes the register in which QRAM returns the corresponding superposition of stored values ​​(data).

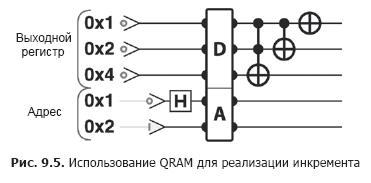
Sample code

This example can be done online at oreilly-qc.github.io?p=9-2 .

Listing 9.2. Using QPU to increment a number from QRAM - the address register can contain superposition, which will cause the output register to contain a superposition of stored values

var a = [4, 3, 5, 1];
var reg_qubits = 3;
qc.reset(2 + reg_qubits + qram_qubits());
var qreg = qint.new(3, 'qreg');
var addr = qint.new(2, 'addr');
var qram = qram_initialize(a, reg_qubits);

qreg.write(0);
addr.write(2);
addr.hadamard(0x1);

qram_load(addr, qreg);
qreg.add(1);

This description of QRAM may seem too vague - what is quantum memory hardware? In this book, we will not give a description of how to build QRAM in practice (as, say, most books on C ++ do not provide a detailed description of how traditional memory works). Code examples like the one in Listing 9.2 are executed using a simplified model that mimics the behavior of QRAM. Nevertheless, prototypes of QRAM technologies exist.



While quantum memory will be a critical component of any serious QPU, implementation details are likely to change, as with any quantum computing device. What is important to us is the very idea of ​​a fundamental resource that behaves as shown in Fig. 9.4, and the powerful applications that can be built on top of it.

With quantum memory at your disposal, you can move on to building complex quantum data structures. Of particular interest are structures that allow you to represent vector and matrix data.

Vector encoding

Let's say you want to initialize the QPU register to represent a simple vector like Equation 9.1.



Formula 9.1. An example of a vector for initializing the QPU register.





Data in this form is often found in quantum machine learning applications.

Perhaps the most obvious method for encoding vector data is to represent each component as a separate QPU register with a suitable binary representation. We'll call this (probably the most obvious) method state encoding for vectors. The vector from the above example can be encoded in four two-qubit registers, as shown in Fig. 9.6.





One of the problems with naive state coding is that it wastes qubits - the most precious resource of a QPU. However, one of the pluses of traditional state-coded vectors is that they do not require quantum memory. The vector components can simply be stored in standard memory and their separate values ​​can be used to control the preparation of each individual QPU register. But this advantage also underlies the most serious flaw in vector state encoding: storing vector data in this traditional way prevents us from using the non-traditional capabilities of QPUs. To use the power of QPU, you need to be able to manipulate the relative phases of superpositions, and this is not easy to do,if every component of a vector actually treats your quantum processor as a collection of traditional binary registers!



Instead, you need to descend to the quantum level. Suppose the vector components are stored in the superposition of the amplitudes of one QPU register. Since a QPU register of n qubits can exist in a superposition with 2n amplitudes (and therefore, for experiments with circular recording, there will be 2n circles), it is possible to represent the encoding of a vector with n components in a QPU register with ceil (log (n)) qubits.



For the vector example from Formula 9.1, this approach would require a two-qubit register - the idea is to find a suitable quantum scheme to encode the vector data in Figure 1. 9.7.





Let's call this unique quantum vector data coding complex amplitude coding. It is important to appreciate the differences between complex amplitude coding and more conventional state coding. Table 9.1 compares the two coding methods for different vector data. The last state encoding example will require four 7-kbit registers, each of which uses a fixed-point representation of Q7.7.



Table 9.1. Differences between vector data coding methods (complex amplitude coding and state coding)





To obtain vectors with complex amplitude coding in QCEngine, you can use the convenient amplitude_encode () function. The program in Listing 9.3 takes a vector of values ​​and a reference to a QPU register (which must be large enough) and prepares that register by performing complex amplitude coding on the vector.

Sample code

This example can be done online at oreilly-qc.github.io?p=9-3 .



Listing 9.3. Preparing vectors with complex amplitude coding in QCEngine

//     ,    
//   2
var vector = [-1.0, 1.0, 1.0, 5.0, 5.0, 6.0, 6.0, 6.0];

//        
//  
var num_qubits = Math.log2(vector.length);
qc.reset(num_qubits);
var amp_enc_reg = qint.new(num_qubits, 'amp_enc_reg');

//      amp_enc_reg
amplitude_encode(vector, amp_enc_reg);

In this example, the vector is simply passed as a JavaScript array stored in traditional memory - even though we have indicated that complex amplitude coding depends on QRAM. How does QCEngine perform complex amplitude coding when only your computer's RAM is available to the program? While it is possible to generate a complex amplitude coding scheme without QRAM, it certainly cannot be done efficiently. QCEngine provides a slow but workable model of what can be achieved with QRAM access.

Limitations of complex amplitude coding

The idea behind complex amplitude coding looks great at first - it uses fewer qubits and provides quantum tools for working with vector data. In any application that uses this mechanism, there are two important factors to consider.

Problem 1: quantum results

You may have already noticed the first of these restrictions: Quantum superpositions generally cannot be read by READ. Our main enemy again! If you distribute the vector components over the quantum superposition, they cannot be read again. Naturally, this does not create any special problems when transferring vector data to the input of another QPU program from memory. But very often, QPU applications that receive complex AM-encoded vector data at the input will also generate complex AM-encoded vector data at the output.



Thus, the use of complex amplitude coding severely restricts our ability to read application output with a READ operation. Fortunately, it is often possible to extract useful information from complex amplitude coding results. As you will see in the following chapters, although you cannot recognize the individual components, you can find out the global properties of vectors encoded in this way. However, complex amplitude coding is not a panacea, and its successful application requires attention and ingenuity.

Problem 2: the requirement to normalize vectors

The second problem associated with complex amplitude coding is hidden in table. 9.1. Take a closer look at the complex amplitude coding of the first two vectors in the table: [0,1,2,3] and [6,1,1,4]. Can the complex amplitudes of a two-qubit QPU register take on the values ​​[0,1,2,3] or the values ​​[6,1,1,4]? Unfortunately not. In previous chapters, we have usually bypassed the discussion of amplitudes and relative phases in favor of a more intuitive circular notation. While this approach was more intuitive, it shielded you from one important numerical rule about complex amplitudes: the squares of the complex amplitudes of a register must add up to 1. This requirement, called normalization, seems logical when you remember that the squares of the amplitudes in the register correspond to the probabilities of reading. different results.Since one result must be obtained, these probabilities (and, consequently, the squares of all complex amplitudes) should add up to 1. When using a convenient circular notation, it is easy to forget about normalization, but it imposes an important constraint on which vector complex amplitude coding can be applied to the data. The laws of physics do not allow creating a register that is in superposition with complex amplitudes [0,1,2,3] or [6,1,1,4].being in superposition with complex amplitudes [0,1,2,3] or [6,1,1,4].which is in superposition with complex amplitudes [0,1,2,3] or [6,1,1,4].



To apply complex amplitude coding to two problem vectors from Table. 9.1, you first need to normalize them by dividing each component by the sum of the squares of all components. For example, in complex amplitude encoding of the vector [0,1,2,3], you first need to divide all components by 3.74 to obtain a normalized vector [0.00, 0.27, 0.53, 0.80], which is now suitable for encoding in complex superposition amplitudes.



Does normalizing vector data have any unwanted effects? It looks like the data has completely changed! In fact, normalization leaves most of the important information unchanged (in geometric representation, it just scales the length of the vector, leaving the direction unchanged). Can we assume that the normalized data completely replace the original data? It depends on the needs of the particular QPU application in which you intend to use them. Remember that you can store the numeric value of the normalization factor in a different register if necessary.

Complex amplitude coding and circular recording

As you begin to think more specifically about the numerical values ​​of the complex amplitudes of the registers, it can be helpful to remind yourself of how complex amplitudes are represented in circular notation, and to notice a possible pitfall. The filled areas in circular notation represent the squares of the amplitudes of the complex amplitudes of the quantum state. In situations such as complex amplitude coding, where the complex amplitudes must represent the components of a vector with real values, this means that the filled areas are determined by the square of the corresponding component of the vector, and not by the component itself. In fig. 9.8 shows how to correctly interpret the representation of the vector [0,1,2,3] after normalization in circular notation.





You now know enough about complex amplitude-coded vectors to understand the QPU applications that will be presented in the book. But for many applications, especially in the field of quantum machine learning, it is necessary to go one step further and use QPU to manipulate not only vectors, but also entire data matrices. How do you encode two-dimensional arrays of numbers?



»More details about the book can be found on the website of the publishing house

» Table of Contents

» Excerpt



For Habitants a 25% discount on coupon - Programming



Upon payment for the paper version of the book, an e-book is sent to e-mail.