Stabilizing video from a moving camera, or how to translate everything into a fixed coordinate system

Computer Vision (CV) capabilities are now completely reshaping the Public Safety solutions market landscape. While it is no longer easy to surprise anyone with traditional video surveillance systems, and it is strange not to find it in any public place, the use of AI in this area is still a novelty.

We are investigating the application of CV to various public safety business tasks. In this post, we offer an option to translate video from a moving camera into a fixed coordinate system for further analysis.

The entire project is on GitHub .

---

Let's say we have some kind of video and we want to build a fixed coordinate system for it in order to evaluate the location of objects relative to each other.

Why is this needed? Very often, in public surveillance tasks, the video that needs to be analyzed is filmed with a moving camera. Because of this, several problems arise in determining the position of objects relative to each other:

• It is not clear what caused the change in the coordinates of the object: the camera or the object itself is moving;
• When changing the scene due to the rotation of the camera, different objects can get the same coordinates, even if the objects were static.

Figure 1 - Identical objects have different coordinates due to camera movement

In order to build a fixed coordinate system, you must:

1. Determine the origin of coordinates;
2. Compare two consecutive frames with each other;
3. , , (, , ..).

2 —

:

1. .
2. : , . . . SIFT, SURF ORB. , . , , , .

3 — matching visualization

1. , .

:

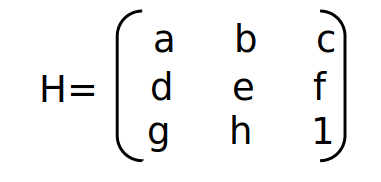
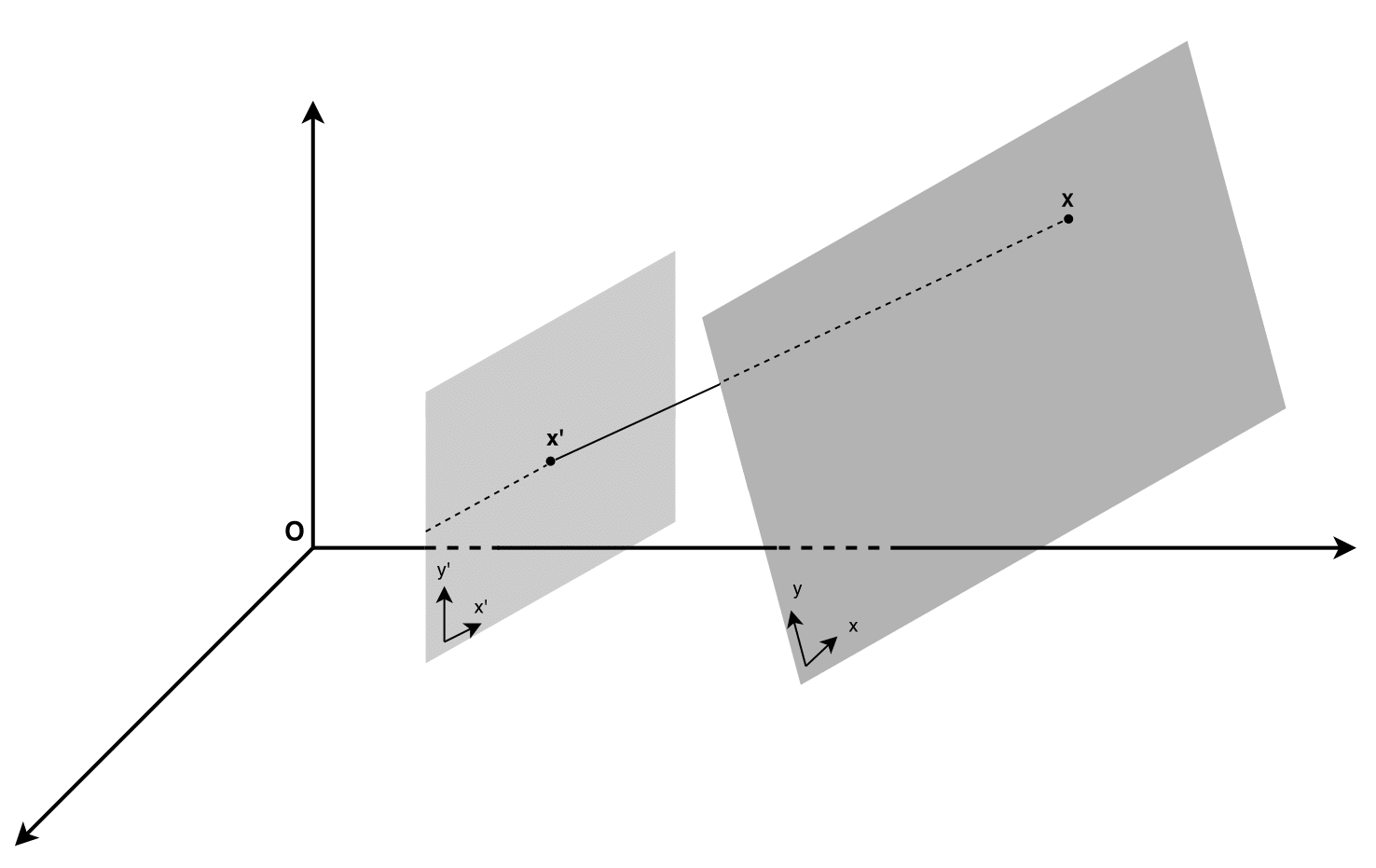
• a, e — x y ;
• b, d — ( a e );
• c, f — ;
• g, h — .

, , . (x,y) (x',y') :

:

$$

$$t\cdot(x',y',1)=H\cdot(x,y,1)(1)$$

:

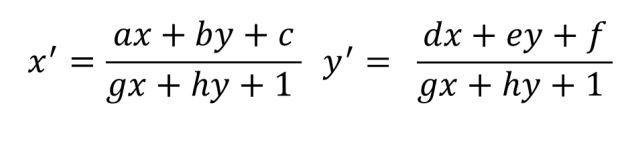
k- .

N — (f₁,..., f_N). . matching points , f_k f_k-1.

:

— ;

(X_k, Y_k)=((x¹_k, y¹_k),…, (xⁿ_k, yⁿ_k)) – n matching points;

(X'_k, Y'_k) =((x'¹_k, y'¹_k),…, (x'ⁿ_k, y'ⁿ_k)) – n matching points ;

(X''_k, Y''_k) =((x''¹_k, y''¹_k),…, (x''ⁿ_k, y''ⁿ_k)) – k — n matching points , f_k-1.

H_k – , f_k-1 f_k.

, .

(X_k, Y_k) (X'_k, Y'_k). f₁ f_k , .. . H_k.

, (H₁,…, H_k-1). H_k (X_k-1, Y_k-1) (X_k, Y_k), , .

3:

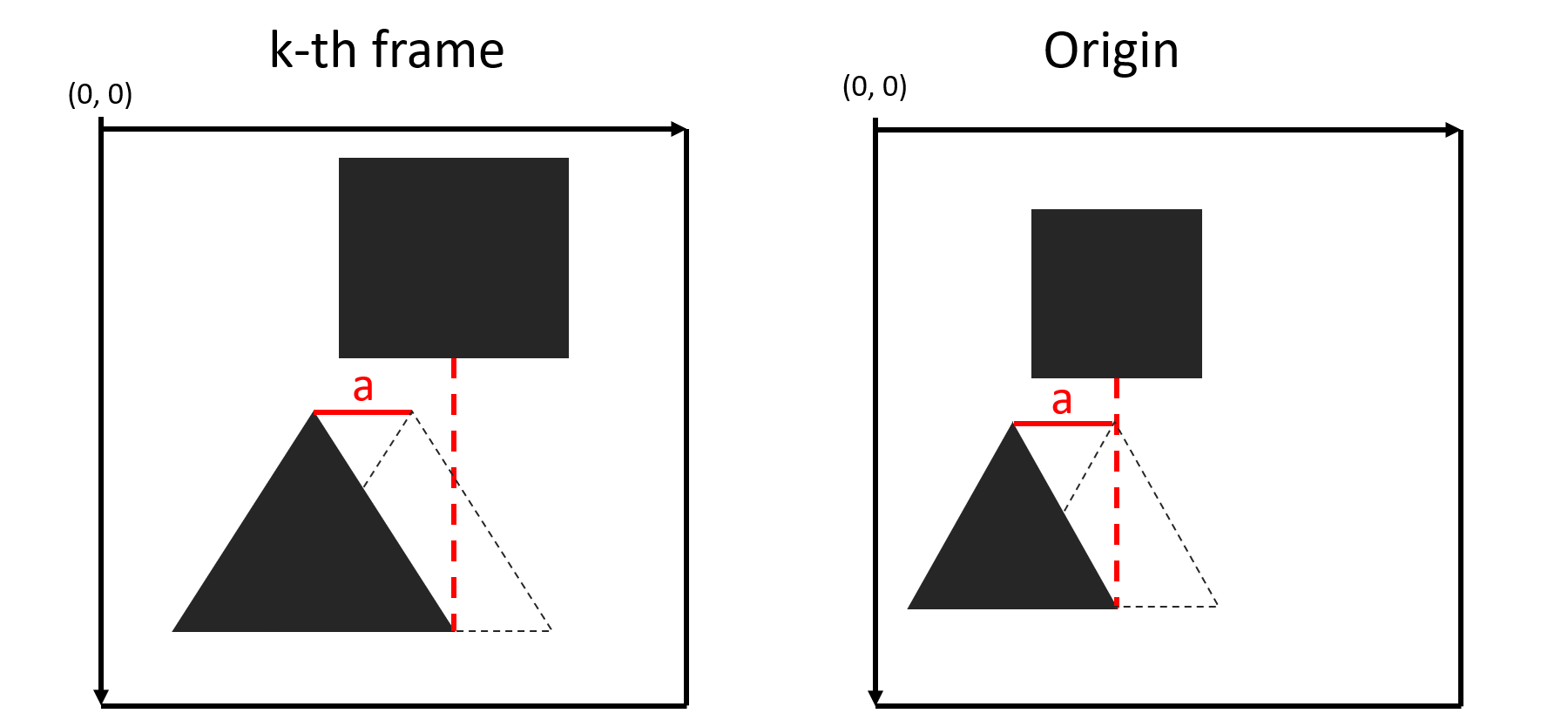
3 — ,



, . a :

x¹_k= x¹_k-1 — a, , a : x'¹_k = x¹_k — a, 3. , , .

?

(H₁,…, H_k-1). , 1 k-1 mathcing points f_k-1 . (1), , — .

$$

$$H_{sup}=H_1\cdot(H_2\cdot(H_3...))(2)$$

, , , f_k-1 f_k, : (X_k-1, Y_k-1) (X_k, Y_k) ( (2)), (X'_k-1, Y'_k-1) (X''_k, Y''_k) H_k. , , (x¹_k, y¹_k) (x'¹_k, y'¹_k).

$$

$$t(x',y',1)=H_{sup} \cdot(x,y,1) (3)$$

: , ( , , .. ), - , . .

:

• "" matching points ((x¹_k, y¹_k),… ,(x'ⁿ_k, y'ⁿ_k)),
• H, k- k-1 .
• ((x'¹_k, y'¹_k),… ,(x'ⁿ_k, y'ⁿ_k))
• :
  
  
  • , ;
  • . , ;
  • - ( LENGTH_ACCOUNTED_POINTS len(matching points)), , , , .

, . .

"" , . , , , , . T , . , motion video segmentation.

.

GitHub , .

• evenvizion_component.py
• evenvizion_visualization.py
• compare_evenvizion_with_original_video.py

evenvizion_component.py

, evenvizion_component.py. , json , f_k-1 f_k. , json , . , , .

- , json --path_to_original_coordinate recalculated_coordinates.json , .

json :

{"frame_no": [{"x1": x coordinate, "y1": y coordinate}, ...], ...}

evenvizion_component.py , 3 ( matching and heatmap --show_matches --visualize_fixed_coordinate_system ).

evenvizion_visualization.py compare_evenvizion_with_original_video.py .

README.

, .

:

matching points — matching visualization:

5 — matching visualization

.

, , (heatmap visualization):

6 — heatmap visualization

20 , , . , . : r=sqrt(x²+y²), heatmap_constant , : 0 — , 1 — .

7 — fixed_coordinate_system_visualization

json , , fixed_coordinate_system_visualization ( 7).

evenvizion_visualization.py compare_evenvizion_with_original_video.py , ( ). 8 9 .

8 — visualize_camera_stabilization

9 — original_video_with_EvenVizion

Known issues

N/a . matching points , , 90 , . video motion segmentation, , , static points motion points. — .

. 4 matching points, , 4 , =None. : none_H_processing True, : H_k=H_k-1. False, H — , . .

. . . :

• . , , (, ).
• findHomography() opencv. .

Thus, we get a component that allows us to estimate the real position of objects relative to each other, to translate the coordinates of the object into a stationary system relative to the frame. Because In this solution, the main thing is to evaluate the transformation of planes using key points, then, as shown above, the problem can be solved even in poor shooting conditions (sharp camera movement, difficult weather conditions, shooting at night, etc.).