Experience in optimizing computations through dynamic JVM bytecode generation

In my small project on simulating random variables, I ran into the problem of low performance in calculating mathematical expressions entered by the user, and for a long time I was looking for different ways to solve it: I tried to write an interpreter in C ++ in the hope that it would be fast, I wrote my own bytecode. The most successful idea turned out to be generating JVM classes and loading them at runtime.



After learning about KMath , I decided to generalize this optimization to a variety of mathematical structures and operators defined on them.



KMath is a library for mathematics and computer algebra that makes extensive use of context-oriented programming in Kotlin. KMath separates mathematical entities (numbers, vectors, matrices) and operations on them - they are supplied as a separate object, an algebra corresponding to the type of operands, Algebra <T> .

import scientifik.kmath.operations.*

ComplexField {
   (i pow 2) + Complex(1.0, 3.0)
}

Thus, after writing a bytecode generator, taking into account JVM optimizations, you can get fast calculations for any mathematical object - it is enough to define operations on them in Kotlin.

API

To begin with, it was necessary to develop an API of expressions and only then proceed to the grammar of the language and the syntax tree. It also came up with the clever idea of ​​defining algebra over the expressions themselves to present a more intuitive interface.



The base of the entire expression API is the Expression <T> interface , and the easiest way to implement it is to directly define the invoke method from the given parameters or, for example, nested expressions. A similar implementation was integrated into the root module as a reference, albeit the slowest.

interface Expression<T> {
   operator fun invoke(arguments: Map<String, T>): T
}

More advanced implementations are already based on MST. These include:

• MST interpreter,
• MST class generator.

An API for parsing expressions from a string to MST is already available on the KMath dev branch, as is the more or less final JVM code generator.



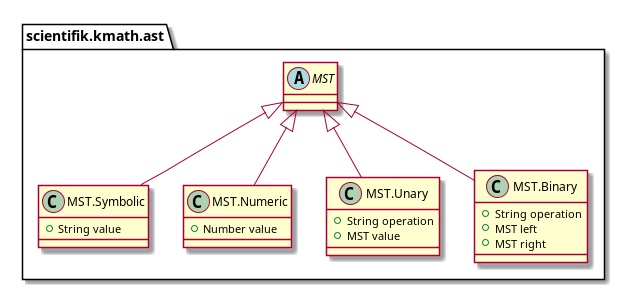
Let's move on to MST. There are currently four kinds of nodes in MST:

• terminal:
  
  
  • symbols (i.e. variables)
  • numbers;
• unary operations;
• binary operations.

The first thing you can do with it is bypass and calculate the result from the available data. By passing in the target algebra the ID of the operation, for example "+", and the arguments, for example 1.0 and 1.0 , we can hope for the result if this operation is defined. Otherwise, when evaluated, the expression will fail with an exception.







To work with MST, in addition to the expression language, there is also algebra - for example, MstField:

import scientifik.kmath.ast.*
import scientifik.kmath.operations.*
import scientifik.kmath.expressions.*

RealField.mstInField { number(1.0) + number(1.0) }() // 2.0

The result of the above method is an implementation of Expression <T> that, when called, causes a traversal of the tree obtained by evaluating the function passed to mstInField .

Generating code

But that's not all: when traversing, we can use the tree parameters as we like and not worry about the order of actions and the arity of operations. This is what is used to generate bytecode.



Code generation in kmath-ast is a parameterized assembly of the JVM class. Input is MST and target algebra, output is Expression <T> instance .



The corresponding class, AsmBuilder , and a few other extensions provide methods for imperatively building bytecode on top of ObjectWeb ASM. They make MST traversal and class assembly look clean and take less than 40 lines of code.



Consider the generated class for the expression "2 * x" , the decompiled Java source code from bytecode is shown:

package scientifik.kmath.asm.generated;

import java.util.Map;
import scientifik.kmath.asm.internal.MapIntrinsics;
import scientifik.kmath.expressions.Expression;
import scientifik.kmath.operations.RealField;

public final class AsmCompiledExpression_1073786867_0 implements Expression<Double> {
   private final RealField algebra;

   public final Double invoke(Map<String, ? extends Double> arguments) {
       return (Double)this.algebra.add(((Double)MapIntrinsics.getOrFail(arguments, "x")).doubleValue(), 2.0D);
   }

   public AsmCompiledExpression_1073786867_0(RealField algebra) {
       this.algebra = algebra;
   }
}

First, the invoke method was generated here , in which the operands were sequentially arranged (since they are deeper in the tree), then the add call . After invoke , the corresponding bridge method was recorded. Next, the algebra field and constructor were written . In some cases, when constants cannot be simply put into the pool of class constants , the constants field , the java.lang.Object array , is also written .



However, due to the many edge cases and optimizations, the generator implementation is rather complicated.

Optimizing calls to Algebra

To call an operation from algebra, you need to pass its ID and arguments:

RealField { binaryOperation("+", 1.0, 1.0) } // 2.0

However, such a call is expensive in terms of performance: in order to choose which method to call, RealField will execute a relatively expensive tableswitch statement , and you also need to remember about boxing. Therefore, although all MST operations can be represented in this form, it is better to call directly:

RealField { add(1.0, 1.0) } // 2.0

There is no special convention on mapping operation IDs to methods in Algebra <T> implementations , so we had to insert a crutch in which it was manually written that "+" , for example, corresponds to the add method. There is also support for favorable situations when you can find a method for an operation ID with the same name, the required number of arguments and their types.

private val methodNameAdapters: Map<Pair<String, Int>, String> by lazy {
    hashMapOf(
        "+" to 2 to "add",
        "*" to 2 to "multiply",
        "/" to 2 to "divide",
...

private fun <T> AsmBuilder<T>.findSpecific(context: Algebra<T>, name: String, parameterTypes: Array<MstType>): Method? =
    context.javaClass.methods.find { method ->
...
        nameValid && arityValid && notBridgeInPrimitive && paramsValid
    }

Another major problem is boxing. If we look at the Java method signatures that are obtained after compiling the same RealField, we will see two methods:

public Double add(double a, double b)

// $FF: synthetic method
// $FF: bridge method
public Object add(Object var1, Object var2)

Of course, it's easier not to bother with boxing and unboxing and call the bridge method: it appeared here because of type erasure, in order to correctly implement the add (T, T): T method , the type T in the descriptor of which was actually erased to java.lang .Object .



A direct call to add from two doubles is also not ideal, because the return value is bauxite (there is a discussion on this in YouTrack Kotlin ( KT-29460 ), but it is better to call it in order to save two casts of input objects to java.lang at best .Number and their unboxing to double .



It took the longest to solve this problem. The difficulty here lies not in creating calls to the primitive method, but in the fact that you need to combine both primitive types (like double) and their wrappers ( java.lang.Double , for example) on the stack , and insert boxing in the right places (for example, java.lang.Double.valueOf ) and unboxing ( doubleValue ) - there was absolutely no work with instruction types in the bytecode.



I had ideas to hang my typed abstraction on top of the bytecode. To do this, I had to dig deeper into the ObjectWeb ASM API. I ended up turning to the Kotlin / JVM backend, examined the StackValue class in detail(a typed fragment of bytecode, which ultimately leads to the receipt of some value on the operand stack), figured out the Type utility , which allows you to conveniently operate with the types available in the bytecode (primitives, objects, arrays), and rewrote the generator with its use. The problem of whether to box or unbox the value on the stack was solved by itself by adding an ArrayDeque holding the types expected by the next call.

  internal fun loadNumeric(value: Number) {
        if (expectationStack.peek() == NUMBER_TYPE) {
            loadNumberConstant(value, true)
            expectationStack.pop()
            typeStack.push(NUMBER_TYPE)
        } else ...?.number(value)?.let { loadTConstant(it) }
            ?: error(...)
    }

conclusions

In the end, I was able to make a code generator using ObjectWeb ASM to evaluate MST expressions in KMath. The performance gain over a simple MST traversal depends on the number of nodes, since the bytecode is linear and does not waste time on node selection and recursion. For example, for an expression with 10 nodes, the time difference between the evaluation with the generated class and the interpreter is 19 to 30%.



After examining the problems I encountered, I made the following conclusions:

• you need to immediately study the capabilities and utilities of ASM - they greatly simplify development and make the code readable ( Type , InstructionAdapter , GeneratorAdapter );
• MaxStack , , — ClassWriter COMPUTE_MAXS COMPUTE_FRAMES;
• ;
• , , , ;
• , — , , ByteBuddy cglib.

Thanks for reading.



Authors of the article:



Yaroslav Sergeevich Postovalov , MBOU “Lyceum № 130 named after Academician Lavrentyev ”, a member of the laboratory of mathematical modeling under the leadership of Voytishek Anton Vatslavovich



Tatyana Abramova , researcher of the laboratory of methods of nuclear physics experiments at JetBrains Research .