
The human body can, without exaggeration, be ranked among the most complex biological systems on the planet. Our body is made up of billions of cells, many organs and systems. But all this splendor and diversity arose due to the fusion of only two cells - a sperm and an egg. I think that there is no need to explain how fertilization takes place and what is required for this (hint - storks and cabbage have nothing to do with it). But here are some aspects of the life of sperm for many years remained unclear. Scientists from the University of Bristol, using modern techniques of three-dimensional microscopy, were able to see the movements of the sperm in a way that was not possible before. How and by what means the sperm moves, we learn from the report of scientists. Go.
Research basis
Despite the fact that sperm were involved in the creation of life long before the advent of the scientific method, their path in the scientific literature began quite recently - in 1677. Medical student Johann Gam shared his observations with colleague and friend Anthony van Leeuwenhoek (1632 - 1723), who, in turn, examined and described in detail the "seminal animals" (as he called spermatozoa).
Anthony van Leeuwenhoek / Lazzaro Spallanzani / Carl Ernst von Baer
Leeuwenhoek suggested that these unusual cells are involved in fertilization, but his theory, although true, was rejected by the scientific community. For a long time it was believed that sperm are parasites, and only seminal fluid is involved in fertilization.
Only almost a hundred years later, in 1786, the fact of the participation of sperm in fertilization was proved by Lazzaro Spallanzani (1729 - 1799) in his work Experiencias Para Servir a La Historia de La Generación De Animales y Plantas. However, his explanations for the process itself were rather vague: he believed that the egg is already the beginning of a new organism, and sperm is needed only to activate the growth process.
The very same term "sperm" was introduced at the beginning of the 19th century by Karl Ernst von Baer (1792 - 1876).
Whatever scientists thought several centuries ago, spermatozoa have a very clear function, the implementation of which is provided by a number of specialized tools. The main task of the human sperm is to pass through the female genital tract, find the egg and transfer the male genetic material to her.

The structure of the sperm The
male reproductive cell cannot boast of dimensions, because it is the smallest in the human body (excluding the tail): the dimensions of the head are 5.0x3.5x2.5 microns (length x width x height), the length of the middle part is 4.5 microns, and tail length - 45 microns.
At the same time, the small size is not a disadvantage, but a thoughtful aspect of increasing its speed. In the process of maturation of the sperm, its nucleus (carries a single set of chromosomes) becomes denser, most of the cytoplasm is discarded, and only the most important organelles remain in the cell.
The flagellum can be called the second most important element of the sperm after the nucleus, i.e. his tail. For it is thanks to him that the movement of this cell along the genital tract of a woman is carried out. It is also funny that the vaginal environment is extremely destructive for male germ cells, but the semen partially reduces the negative effect on sperm. The pH level inside the female genital tract allows sperm to move towards the uterus, where a much more favorable environment awaits them.
Previously, it was believed that the sperm moves forward due to the symmetrical movement of its flagellum from side to side.
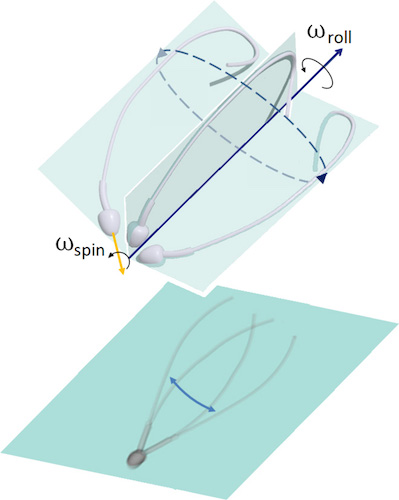
Image # 1: asymmetry of flagellar movement in 3D (top); planar projection of the flagellum movement, creating an optical illusion of bilateral symmetry in 2D microscopy (from below).
This statement was expressed even in the days of Levenguk. It also led to a symmetrical idealization of the waveform in three dimensions, often perceived as a conical spiral, similar to an expanding corkscrew.
Due to two-dimensional microscopy, many observations have been interpreted inaccurately, and sometimes completely wrong. The statements regarding the symmetry of the flagellum flaps contradict many observations showing the structural asymmetry within the framework of the flagellum itself.
If the flapping of the sperm flagellum during movement is still asymmetric, then how is the symmetry of the flagellum movement from side to side and the movement of the cell in the forward direction achieved? It is this question that is the main one in this study.
To get an answer to this, the scientists compared molecular and microscopic observations that showed that the human sperm uses both asymmetric and anisotropic control to regulate flagellar flapping. In other words, symmetry is realized due to asymmetry: the effect of a "precessing top" occurs when the head rotates ("drilling fluid", the words of the authors) simultaneously and regardless of how the sperm flagellum rotates around the axis of motion.
Research results
The rapid movement of human sperm flagella has been recorded with high spatial and temporal resolution in 3D. Two groups of free-floating spermatozoa in a low-viscosity fluid were examined: spermatozoa that float next to the coverslip (lies on top of the specimen during microscopy) and away from it.
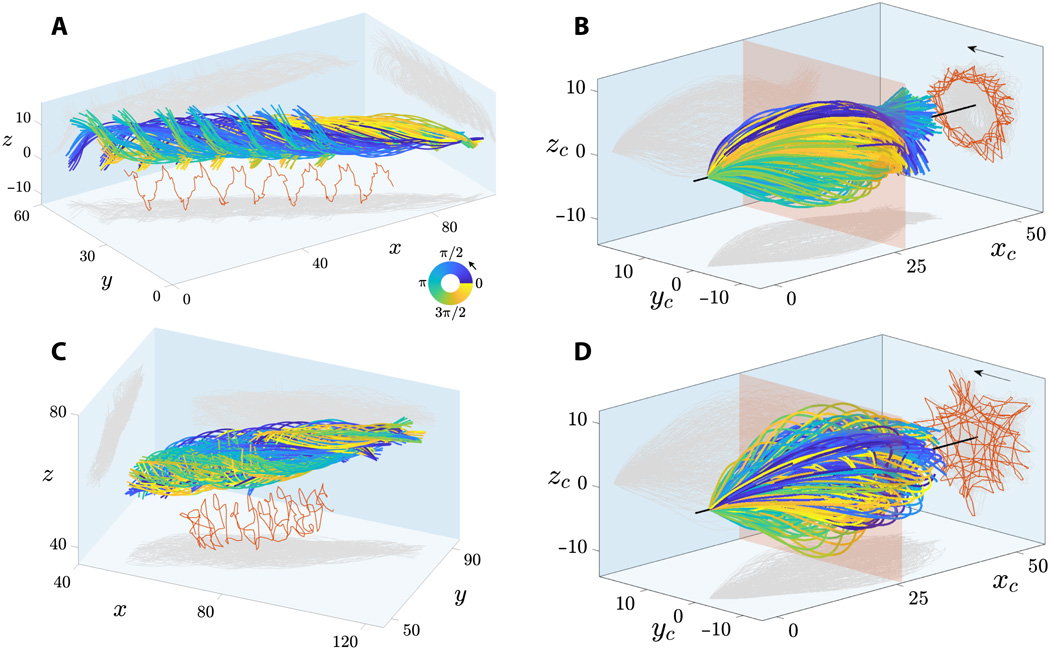
Image №2
On 2A and 2C show sweeps sperm flagella floating near and far from the coverslip. Flagellum flaps are characterized by a characteristic rolling motion around the direction of movement of the sperm.
The combined rotation and translational movement of the sperm flagellum leads to spiral trajectories of the midpoint of the flagellum with preserved chirality (marked in red at 2Aand 2C ). Spermatozoa show bi-directional rotation around their axis: all freely floating cells (28 pieces) rotated counterclockwise when viewed from the front end (arrows on 2B and 2D ) and only 2 cells rotated clockwise (they did not move forward due to obstacles on their way).
Microscopy of spermatozoa floating next to the coverslip (corresponds to 2A ).
All spermatozoa (30 cells) moved similarly to a precessing spinning top, in which the rotation of the head around the longitudinal axis of the sperm cell (ω spin ) occurs simultaneously and regardless of how the flagellum rotates relative to the axis of motion (ω roll ).
At 2B and 2D shows flapping flagellum terms of concomitant * coordinate system , i.e. a viewing point, moves together with the sperm, but not rotary motion around its axis. This shows that flagellar strokes are extremely symmetric both in the planar ( xy ) and out-of-plane (z ) directions, which corresponds to observations in 3D.
The accompanying frame of reference * is a frame of reference associated with the body in question at a certain specific moment. The body inside this system is motionless. For example, a freely falling elevator is an accompanying frame of reference for a body freely falling in it, but the Earth is not such a system in relation to the body in an elevator.The projection of the trajectory of the middle of the flagellum (red lines in 2B and 2D ) reveals an incredible array of geometric patterns, from rotating stars to triangles, squares, and loop patterns with polar symmetry. The irregular flagellar pattern shown in 2D for spermatozoa floating off the coverslip is also observed for sperm floating next to the coverslip. This variability in patterns can be caused by a mismatch in the phase lag between the in-plane and out-of-plane components of the flapping for each cell, which increases in the rolling motion timeline. Consequently, flagellar patterns are not a distinguishing feature of cells floating near and far from the coverslip.
Microscopy and modeling of the flagellum showing rotation of the head and flagellum around the axis of motion.
The amplitude of the 3D wave is characterized by a symmetrical bullet-shaped envelope curve, as opposed to the conical spiral (similar to an expanding corkscrew), which is often described in the literature. Spermatozoa that float away from the coverslip had a more symmetrical waveform than cells floating next to the glass. Thus, the adjacent coverslip is a weak source of asymmetry for flagellar flapping.
Spermatozoa floating next to the coverslip had a preserved angle of attack * -7 °, with an average orientation of the sperm flagellum directed towards the coverslip.
* — ( ) , .

Image # 3
The image above shows a comparison of flagellar strokes in the companion frame (top row) and the accompanying rolling frame (bottom row).
Figure 3E shows the true nature of the flagellar beat as seen from the sperm perspective, without any floating or rolling movement.
The accompanying rolling reference frame ( 3E ) shows that the flagellar flaps are anisotropic, i.e. wave characteristics in each transverse direction (perpendicular to the flapping plane), labeled “ b plane” (blue plane) and “ z plane” (red plane), are markedly different.
If we compare the light gray areas on the blue and red planes at 3E, then it can be seen that the flapping is strongly asymmetric in the b plane and is characterized by a broken left-right symmetry, reminiscent of a C-shape.
This observation is in strong contrast to the symmetric patterns observed in the comoving reference frame at 3A .
Flagellar waveform relative to a laboratory fixed frame of reference (x, y, z).
Principal component analysis (PCA) of a three-dimensional waveform has allowed scientists to decompose the flagellar wave into several "basic shape modes," referred to here as PCA modes. The 3D waveform can be reconstructed with good accuracy with only two waveform modes, as seen with 3B and 3F .
In 3C, it can be seen that the first two PCA modes are identical in shape, up to a 90 ° rotation, thus capturing the streamlined spiral shape caused by the rolling of the sperm.
On 3G , however, the internal asymmetric C-shape is fully detected only by the first PCA mode. Second PCA mode on 3G(highlighted in orange) introduces small deviations perpendicular to the first PCA mode (highlighted in blue), indicating that the waveform can be decomposed into two independent transverse waving directions that are anisotropic in nature.
Fourier analysis of the sweeps made it possible to reconstruct the movement of the flagellum using only two Fourier modes on 3D and 3H . In short, each common sweep signal can be approximated by a simple sum of two functions:
f r (s, t) ≈ f 0 (s) + | f 1 (s) | sin (ωt + φ (s))The first function f 0 (s) does not depend on time, it is called the "static mode", and it fixes the averaged signal asymmetry along the length of the flagellum arc (s).
The second function is a sinusoidal traveling wave, called "dynamic mode," oscillating at the frequency captured by the first peak of the signal's power spectrum.
The amplitude and phase modulation of a traveling wave along the flagellum are equal, respectively, | f 1 (s) | and φ (s) = arg (f 1 (s)).
Thus, the phase carries information about the characteristics of the traveling wave. For example, if the phase φ (s) does not change along s, then the signal is not a traveling wave, but rather a standing wave.
Hence, static mode captures any waveform mismatch. In this case, the black straight line in 3D reflects the symmetry of the sweep in the xy and xz planes in the comoving frame. In contrast, in the accompanying rolling reference frame ( 3H ), the static mode (black curve) is characterized by a large asymmetric amplitude, reminiscent of an inverted C.
Flagellum waveform relative to the accompanying frame of reference.
Waveform of the flagellum relative to the accompanying rolling reference frame.
The dynamic mode in the companion frame (red curves) in 3D has a large amplitude and is highly symmetric in the xy and xz planes due to the rolling of the sperm.
But the dynamic mode in the accompanying rolling reference frame (red curves) at 3H has a reduced waveform amplitude and a preferred direction of travel.
The Fourier reconstruction of the waveform was performed by summing the static and dynamic modes (graphs in the center on 3D and 3H ), which is in good agreement with the original observations (graphs on the right in 3Dand 3H ).
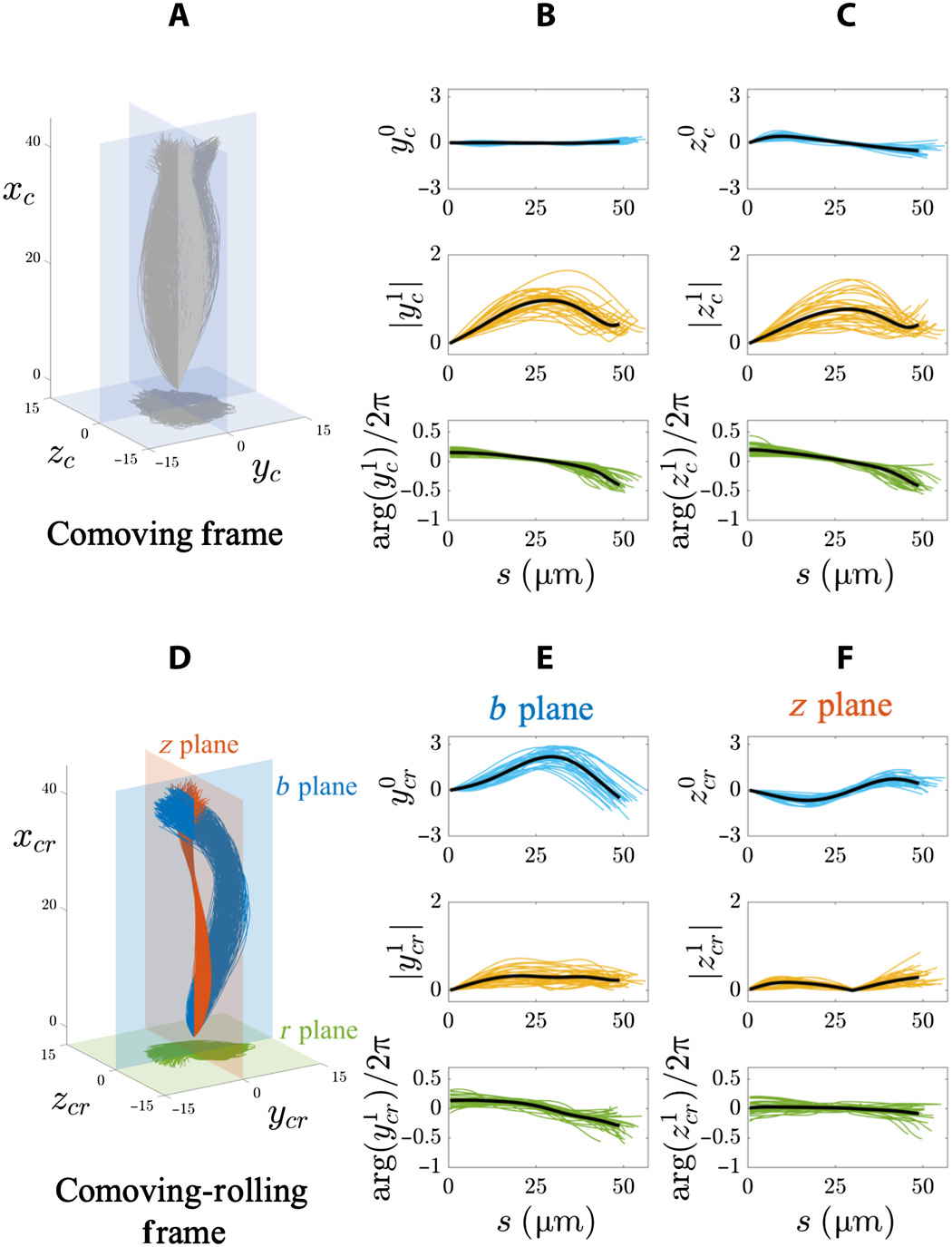
Image # 4 The
graphs above show the results of a Fourier analysis of a 3D flagellar flap in a free-floating sperm population (20 cells next to the coverslip and 8 cells away from the glass). In the accompanying frame of reference ( 4A - 4C ), the amplitudes of the static mode in both directions (y c and z c ) are very small (top row of graphs at 4B and 4C ) due to the symmetry of the sweeps.
In addition, the amplitude (middle row) and phase (bottom row) of dynamic modes (y c and z c ) at 4B and 4Cfixes transverse symmetry and exceeds isotropy in this frame of reference due to the fact that the spermatozoon rotates around the axis of motion.
The characteristics of the traveling wave for both coordinates (y c and z c ) are the same for all freely floating cells: frequency 4 Hz, wavelength 100 μm, and wave speed 400 μm / s.
In the accompanying rolling reference system ( 4D - 4F ), distinct static regimes in the b and z planes show that the swings still have anisotropy in a free floating cell population ( 4E and 4F ).
Static mode b plane (y cr) is strongly asymmetric and biased towards positive values (top row of graphs by 4E ). But for the z plane (z cr ), it oscillates symmetrically along the length of the arc in a sinusoidal manner (top row at 4F ).
The amplitude of the dynamic regime in the b plane (y 1 cr ) increases until reaching a plateau (middle row at 4E ), while the dynamic regime in the z plane (z 1 cr ) is nonmonotonic along the arc length (middle row at 4F ). Traveling wave characteristics y cr ( bplane) were: frequency 8 Hz, wavelength 145 μm and wave speed 1120 μm / s. Characteristics of a traveling wave z cr ( z plane): frequency 6 Hz, wavelength 1526 μm, and speed 5174 μm / s.
Small changes in phase at large distances along the entire length of the flagellum require very high wave propagation velocities. Consequently, the oscillations of the z plane actually behave like a standing wave pulsating in time.
Microscopy of non-propelling and rolling spermatozoa.
The totality of the above data suggests that flagella flapping uses two coactive anisotropic transverse controls, which are not too different from traveling electromagnetic waves. However, each shear wave (y cr , z cr ) is the sum of static and dynamic modes: an asymmetric traveling wave along the b plane (blue at 4D ) and a symmetric standing wave in the z plane (red at 4D ).
It is curious (but not surprising) that the presence of a cover glass near the trajectory of the sperm cell also has its effect on the amplitude of wave propagation.

Image No. 5
Glass reduces the amplitude of wave propagation due to hydrodynamic interactions between the flagellum and the hard surface of the cover glass.
In the companion frame ( 5A and 5B ), the amplitude of both dynamic modes (y c , z c ) decreases towards the end of the sperm flagellum near the coverslip (graphs in the center), while the static modes remain unchanged (graphs top).
The dynamic mode z c is only slightly less than y c (blue curves) in the center plots 5A and 5B . This contrasts with the symmetrical, unchanging profiles of both (yc , z c ) dynamic modes for spermatozoa detected away from glass (red curves in the graphs in the center 5A and 5B ).
If we pay attention to the accompanying rolling reference system, then the nature of the glass effect is quite anisotropic, since it affects only one rolling plane, i.e. on the b plane ( 5C ).
The cover slip affects both static and dynamic y cr modes (graph above and in center at 5C ). But the z plane (z cr ) remains unchanged (graph at the top and center at 5D ).
The shape of the static mode in the companion rolling reference system is the same among all spermatozoa and defines an off-center right-handed spiral indicated by h (s) and shown by the black curve at 5E . The projection of the spiral onto the rolling plane (green plane) is a counterclockwise spiral that has no polar symmetry, i.e. offset to one side (gray projection at 5E ).
The static mode spirals strongly resemble the logarithmic spirals that are often found in nature. However, in this case, the radius of the spiral changes non-monotonically, increasing / decreasing at a faster rate than that of logarithmic spirals elsewhere in nature.
Right-hand logarithmic spiral h (s) at 5Ecan be expressed in terms of its radius and pitch ( 5G ), which decays exponentially along the length of the flagellum. Any change in sign in h y or h z causes the spiral to switch to clockwise rotation, thus creating a left-handed spiral. All free floating spermatozoa generated counterclockwise spirals. Only two spermatozoa had clockwise spirals, albeit with a shape identical to 5E . It was these two cells that could not swim forward because of some obstacles in their path, but they could continue to rotate around their own torsion axis.
In all cases, the rotation of the helix correlates with the direction of sperm rolling as follows: a counterclockwise helix for clockwise rotation (as viewed from the rear end) and a clockwise helix for counterclockwise rotation.
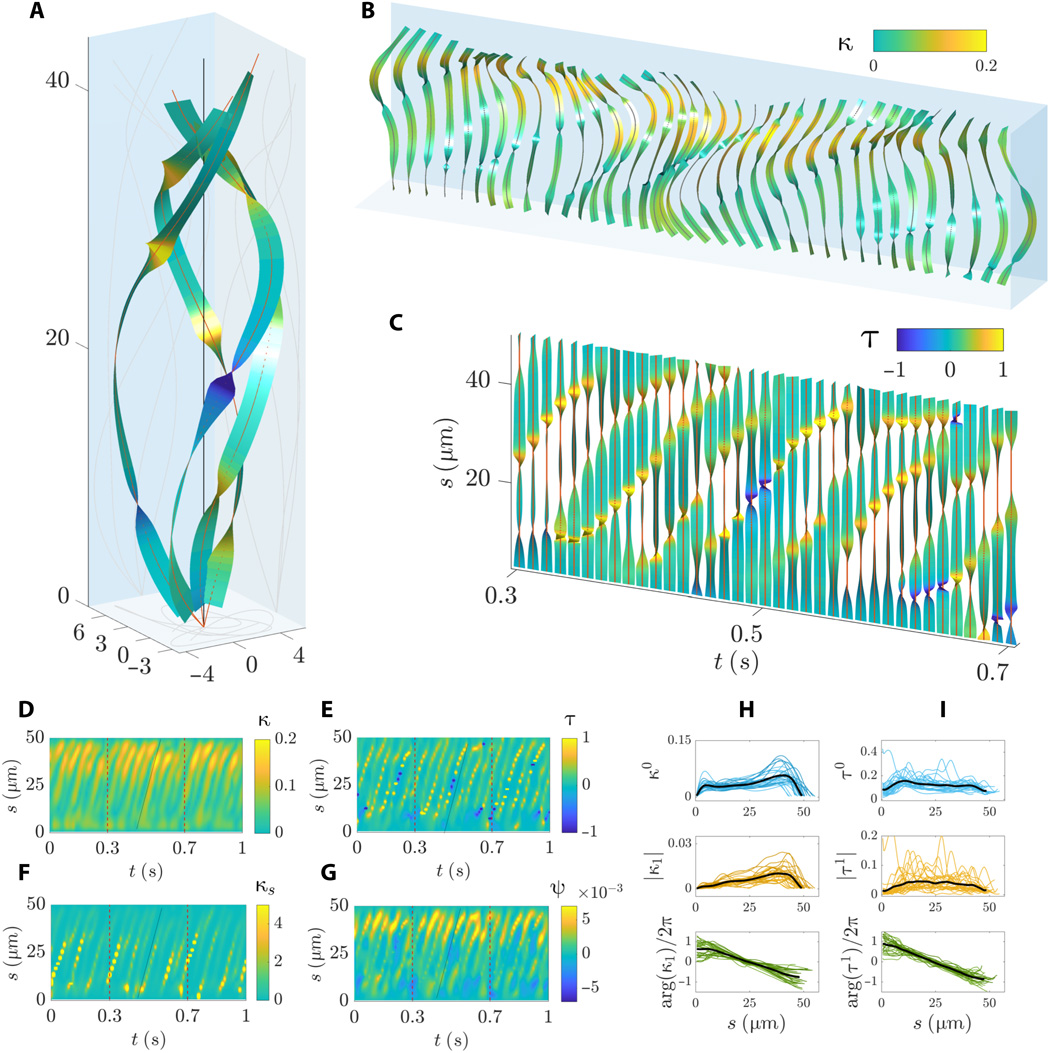
Image # 6
Graphs 6A and 6B show a complex sequence of traveling waves as the flagellum rotates around its rolling axis. Flexural waves propagate linearly along the flagellum with a non-monotonic amplitude along the arc length, characterized by a sharp increase in the middle and distal regions.
The twisting of the waveform is characterized by sharp bends along the arc length ( 6B and 6C) with simultaneous positive and negative turns. The spiral shape of the central line of the flagellum undergoes a phenomenon whereby regions of opposite chirality along the flagellum coexist. However, portions of the flagellum with opposite chirality move during flapping ( 6C and 6E ). Traveling torsion waves propagate at the same speed as the curvature wave.
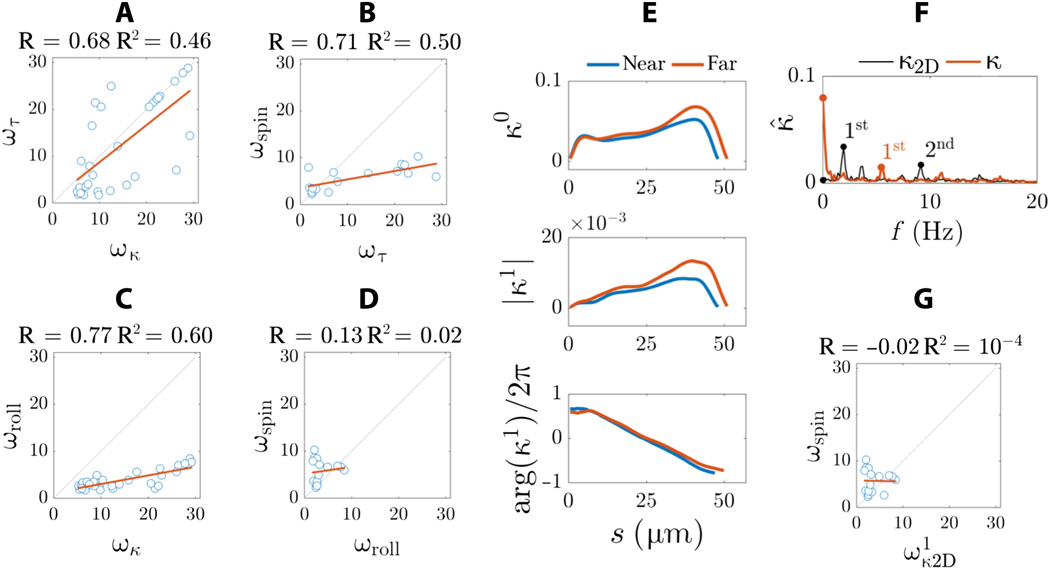
Image # 7
To better understand the difference between the 3D microscopy results obtained in this study and the 2D microscopy results that are often described in the literature, scientists created a 2D projection from a 3D waveform.
The static regime of two-dimensional curvature is very insignificant ( 7F). In 2D, the intrinsic asymmetry of the waveform cannot be detected. Instead, the frequency spectrum is characterized by two frequency peaks (black markers at 7F ) rather than one major frequency peak seen for three-dimensional curvature (red curve at 7F ).
For a more detailed acquaintance with the nuances of the study, I recommend that you look into the report of scientists and additional materials to it.
Epilogue
In this work, scientists were able to show in practice that due to three-dimensional microscopy it is possible to find out what two-dimensional microscopy will not give - for example, to see changes in the direction of the spiral (changes in chirality) during the oscillation of the flagella.
At first glance, it may seem that the sperm are simply floating forward, wagging their tails. However, a detailed examination of the kinematics of these cells showed that this process is much more complicated. The flapping and swaying of the flagella, the rotation of the cell itself - all this together allows the sperm to move forward.
Some of this information was previously available, but not all of the details have been detailed due to the limitations of 2D microscopy. Understanding how sperm move can help a lot in the field of reproductive medicine, scientists say. In particular, the new data will expand the range of parameters by which unhealthy sex cells of men are determined, which is the cause of infertility in about half of the couples.
In any case, the better we understand certain phenomena and processes, especially those taking place in our own body, the more likely it is to improve the quality of our life.
Thanks for your attention, stay curious and have a good work week, guys. :)
A bit of advertising
Thank you for staying with us. Do you like our articles? Want to see more interesting content? Support us by placing an order or recommending to friends, cloud VPS for developers from $ 4.99 , a unique analogue of entry-level servers that we have invented for you: The Whole Truth About VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps from $ 19 or how to divide the server correctly? (options available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).
Is Dell R730xd 2x cheaper in Equinix Tier IV data center in Amsterdam? Only we have 2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 TV from $ 199 in the Netherlands!Dell R420 - 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB - From $ 99! Read about How to build the infrastructure of bldg. class with Dell R730xd E5-2650 v4 servers at a cost of 9000 euros for a penny?