Symplectic geometry is a relatively new field of study, influencing much of modern mathematics. And that's what it is.

In the early 19th century, William Rowan Hamilton discovered a new geometric space with almost magical properties. It encoded motion and mathematics into a single beautiful geometric object.
From this phenomenon a field of knowledge has grown called symplectic geometry . Over the past few decades, it has grown from a few collections of ideas to a dynamic field of research with deep connections to more topics in mathematics and physics that Hamilton could hardly have imagined.
Symplectic geometry, in fact, is the study of geometric spaces of symplectic structure. However, it should be clarified what it means that space has a structure - not to mention any particular structure.
Geometric spaces can be flexible like a tarp or rigid like a tent. “A tarp is a flexible thing, but if you take a bunch of sticks and arrange a frame for it, you get a more stable structure,” said Amy Murphy of Northwestern University.
Less structured spaces are just a bunch of connected dots (like a tarp). The straight line is an example of a one-dimensional space of this kind. The surface of a ball is a two-dimensional example. Since there is no structure in these spaces, it is easy to deform them without changing at a fundamental level. Curve a straight line; inflate, crumple, twist the ball - from the point of view of topology, studying unstructured spaces, they will not change.
“From the point of view of topologists, starting with the surface of a ball, you can stretch it as you like, and until you break it, that space does not change for them,” said Isa Keating of the University of Cambridge. "They are interested in the general characteristics of the figure."
Naturally, when mathematicians talk about the deformation of space, they do not mean changing it manually. They change spaces using functions: the function includes the coordinates of a point, and the coordinates of a new point come out. Such transformations translate any point in space into a new one. This is the mathematical equivalent of shaking a tarp.
You can add structure to the space. This structure reinforces the information contained in the space, while limiting the possibilities for its deformation.

Unstructured space: the surface of the ball is two-dimensional space. The absence of a structure gives ample opportunities for its deformation without changing its topological properties.

Adding structures: By adding a metric structure to the space - let's say, like the lines of latitude and longitude on a globe - we can measure distances between points. But then there will be only a small set of options for object deformation that do not violate these distances.
You can, for example, add a metric structure to the surface of a sphere, like the lines of latitude and longitude on a globe. This structure will allow us to measure the distances between points. But after its application, it will no longer be possible to inflate or crumple the ball without breaking the original structure - after all, then we will change the distances between the points. If we inflate the balloon, the distance between New York and London, for example, will increase.
We can add another kind of structure - symplectic. It gives us the ability to measure areas in space, and allows us to change the shape of space so that these areas do not change.
The first example of such a space was found by Hamilton while studying physical systems- for example, planetary movements. When a planet moves in space, its location is determined by three coordinates that determine its position along the x, y and z axes. The points representing all possible planetary locations form three-dimensional space.
Hamilton discovered that each point in this three-dimensional space can be assigned three additional coordinates, denoting the magnitude of the planet's momentum along the three axes. Let's call them x m , y m and z m . We now have six coordinates: three for location and three for momentum. These six coordinates define a point in the new six-dimensional space.

We have six coordinates: three for location and three for momentum. These six coordinates define a point in the new six-dimensional space.
This six-dimensional space is an example of a space with a symplectic structure, since it has the ability to measure areas. And here's how it works.
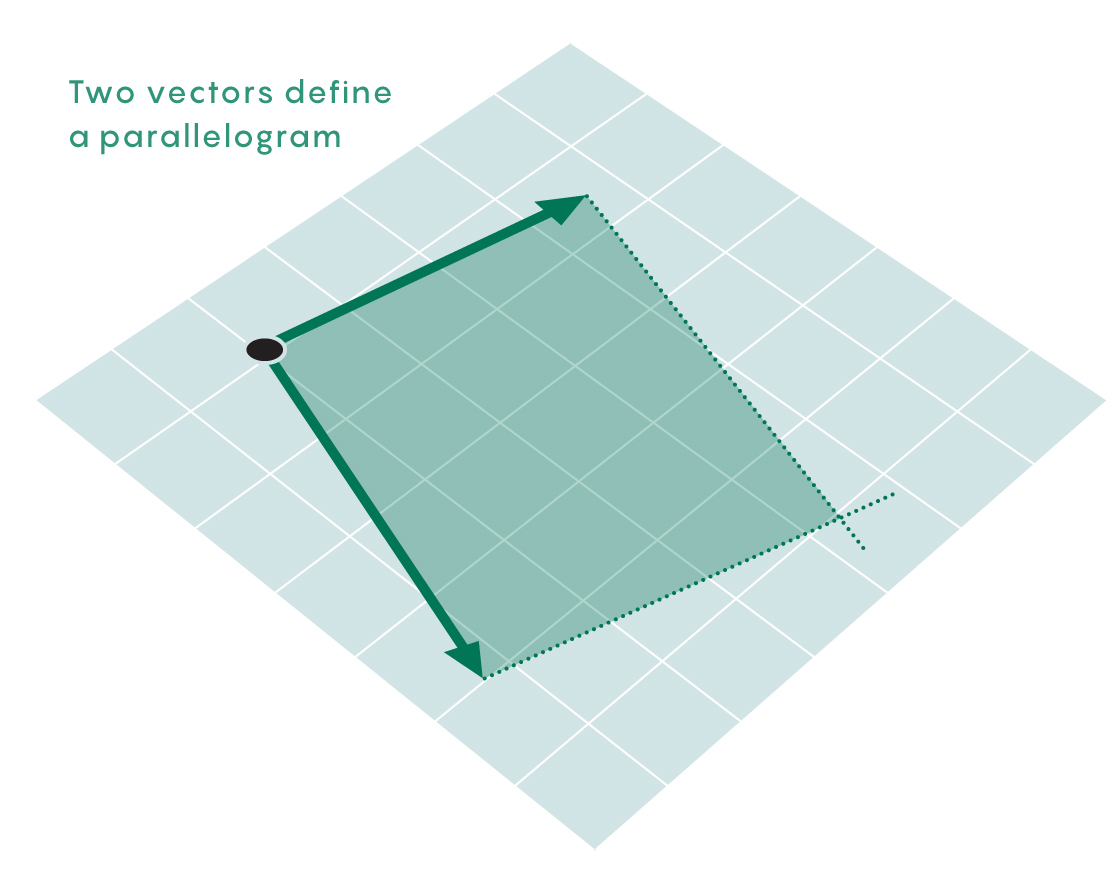
At each point in space, you can draw six vectors (directional arrows) corresponding to the direction of motion or momentum of the planet along the dimension where the vector points. Since two vectors form a parallelogram - a two-dimensional space with non-zero area - you can take two vectors and measure that area.
To ensure that the value is non-zero, you need to take certain pairs of vectors - denoting the direction of movement and momentum along the same axis. Mismatched vectors, for example, the z-axis directional vector together with the y-axis momentum vector give a parallelogram with zero area.
Such pairs of vectors also reflect another important property of symplectic space - their relationship with complex numbers. These numbers have i, the square root of -1, and are of the form a + bi, where a is real and b is imaginary. One way to define a six-dimensional symplectic space is to define three complex numbers, two parts of each giving one coordinate. These two parts also correspond to the two vectors that we combine to measure the area.
So for each point, for example, the vectors of direction of motion and momentum plotted along the x-axis not only provide a way to measure area, but also make up one of the three complex numbers that define space. This relationship is reflected in the name, because "symplectic" comes from the Greek word sumplektikós, which means the same as the Latin complex - "entwined together." The name reflects the intertwining of symplectic structure and complex numbers.
It is also one of the main reasons why symplectic space captures the imagination of mathematicians. “Mathematicians were already interested in complex numbers and planetary motions,” Murphy said. "So if you tell a mathematician about the existence of geometry, which shows why these two things are different manifestations of the same basic structure, he will certainly be interested in this issue."
Symplectic geometry studies transformations of spaces that preserve their symplectic structure and do not change the size of the areas. This restriction does not give very much leeway for the allowed transformations. As a result, symplectic geometry occupies an intermediate position between flexible tarpaulin topology and rigid tent geometry. Transformations that preserve the symplectic structure are called, after the discoverer, Hamiltonian diffeomorphisms .
However, Hamilton discovered only the first example of a symplectic space, and there was no reason to dwell on this. Soon, mathematicians began to think about what symplectic phenomena might look like in geometric spaces unrelated to the physical world.
"Mathematicians always strive for generalizations, we want to ask: what would classical mechanics look like if we lived not in three-dimensional, but in eight-dimensional space?" Murphy said.

Vladimir Igorevich Arnold put forward several basic hypotheses in the field of symplectic geometry
In the 1960s, Vladimir Igorevich Arnoldput forward several influential hypotheses describing certain properties of symplectic space that make them more rigid than ordinary topological ones. One of them, Arnold's conjecture on fixed points of symplectomorphisms, predicts that Hamiltonian diffeomorphisms have an unexpectedly large number of “fixed” points that do not change their location during transformations. Studying them, we can say for sure what distinguishes symplectic space from other types of geometric spaces.
In the late 1980s, German mathematician Andreas Floerdeveloped Floer homology, a powerful platform that mathematicians use today to study symplectic phenomena. She uses the so-called. pseudoholomorphic curves, which indirectly allow mathematicians to count the number of fixed points, determining a certain minimum number of them that a symplectic space should have.
“Floer homology shows that you can't just drop fixed points,” Keating said. "It allows you to prove that these points must be there."
As the theory of symplectic geometry developed, links were found to an ever-growing range of topics in mathematics and physics, from string theory to low-dimensional topology and the study of a confusing mathematical duality called mirror symmetry. One recent example of the application of symplectic geometry is the solution of the topological square peg problem .
For many mathematicians, however, the appeal of symplectic geometry has little to do with its intersections with physics or other areas of mathematics. They consider her very existence a miracle. “We begin to find beauty in the structure itself, regardless of its relationship to anything else,” said Murphy.