The purpose of this article is to talk about linear regression, namely, to collect and show the formulations and interpretations of the regression problem in terms of mathematical analysis, statistics, linear algebra and probability theory. Although the textbooks set out this topic strictly and exhaustively, another popular science article will not hurt.
! Watch out for traffic! The article contains a noticeable number of images for illustrations, some in gif format.
Content
- Introduction
- Least square method
- Mathematical analysis
- Statistics
- Probability theory
- Multilinear regression
- Linear algebra
- Arbitrary basis
- Concluding remarks
- Dimension selection problem
- Numerical methods
- Advertising and conclusion
Introduction
There are three similar concepts, three sisters: interpolation, approximation and regression.
They have a common goal: from a family of functions, choose the one that has a certain property.
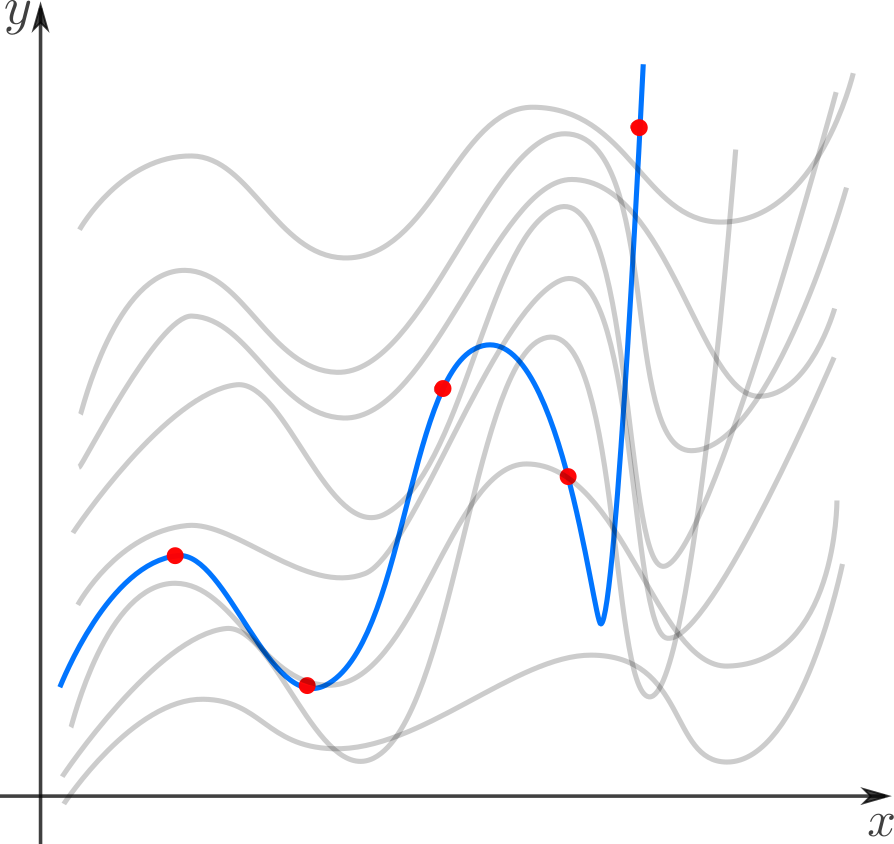
Interpolation- a way to select from a family of functions the one that passes through the given points. The function is then usually used to calculate at intermediate points. For example, we manually set the color to several points and want the colors of the remaining points to form smooth transitions between the given ones. Or we set keyframes for the animation and want smooth transitions between them. Classic examples: Lagrange polynomial interpolation, spline interpolation, multidimensional interpolation (bilinear, trilinear, nearest neighbor, etc.). There is also a related concept of extrapolation - predicting the behavior of a function outside of an interval. For example, predicting the dollar rate based on previous fluctuations is extrapolation.
 Approximation- a way to choose from a family of "simple" functions an approximation for a "complex" function on a segment, while the error should not exceed a certain limit. Approximation is used when you need to get a function similar to a given one, but more convenient for calculations and manipulations (differentiation, integration, etc.). When optimizing critical sections of the code, an approximation is often used: if the value of a function is calculated many times per second and absolute accuracy is not needed, then a simpler approximant with a lower "cost" of calculation can be dispensed with. Classic examples include Taylor series on a segment, orthogonal polynomial approximation, Padé approximation, Bhaskar sine approximation, etc.
Approximation- a way to choose from a family of "simple" functions an approximation for a "complex" function on a segment, while the error should not exceed a certain limit. Approximation is used when you need to get a function similar to a given one, but more convenient for calculations and manipulations (differentiation, integration, etc.). When optimizing critical sections of the code, an approximation is often used: if the value of a function is calculated many times per second and absolute accuracy is not needed, then a simpler approximant with a lower "cost" of calculation can be dispensed with. Classic examples include Taylor series on a segment, orthogonal polynomial approximation, Padé approximation, Bhaskar sine approximation, etc.
 Regression- a way to choose from a family of functions the one that minimizes the loss function. The latter characterizes how much the trial function deviates from the values at the given points. If points are obtained in an experiment, they inevitably contain measurement error, noise, so it is more reasonable to require that the function convey the general trend, and not exactly pass through all the points. In a sense, regression is an “interpolating fit”: we want to draw the curve as close to the points as possible and still keep it as simple as possible to capture the overall trend. The loss function (in the English literature “loss function” or “cost function”) is responsible for the balance between these conflicting desires.
Regression- a way to choose from a family of functions the one that minimizes the loss function. The latter characterizes how much the trial function deviates from the values at the given points. If points are obtained in an experiment, they inevitably contain measurement error, noise, so it is more reasonable to require that the function convey the general trend, and not exactly pass through all the points. In a sense, regression is an “interpolating fit”: we want to draw the curve as close to the points as possible and still keep it as simple as possible to capture the overall trend. The loss function (in the English literature “loss function” or “cost function”) is responsible for the balance between these conflicting desires.
In this article, we'll look at linear regression. This means that the family of functions from which we choose is a linear combination of predetermined basis functionsf i
f = ∑ i w i f i .
Regression has been with us for a long time: the method was first published by Legendre in 1805, although Gauss came to it earlier and used it successfully to predict the orbit of the "comet" (actually a dwarf planet) Ceres. There are many variations and generalizations of linear regression: LAD, Least Squares, Ridge Regression, Lasso Regression, ElasticNet, and many others.

GoogleColab.
GitHub
Least square method
Let's start with the simplest two-dimensional case. Let us be given points on the plane{ ( x 1 , y 1 ) , ⋯ , ( x N , y N ) } and we are looking for such an affine function
f ( x ) = a + b ⋅ x ,
 so that its graph is closest to the points. Thus, our basis consists of a constant function and a linear( 1 , x ) .
so that its graph is closest to the points. Thus, our basis consists of a constant function and a linear( 1 , x ) .
As you can see from the illustration, the distance from a point to a straight line can be understood in different ways, for example, geometrically - it is the length of a perpendicular. However, in the context of our task, we need a functional distance, not a geometric one. We are interested in the difference between experimental value and model prediction for eachx i , so you need to measure along the axisy .
The first thing that comes to mind is to try an expression that depends on the absolute values of the differences as a loss function| f ( x i ) - y i | ... The simplest option is the sum of the deviation modules∑ i | f ( x i ) - y i | results in Least Absolute Distance (LAD) regression.
However, the more popular loss function is the sum of the squares of the deviations of the regressant from the model. In English literature, it is called Sum of Squared Errors (SSE)
SSE(a,b)=SSres[iduals]=N∑i=1i2=N∑i=1(yi−f(xi))2=N∑i=1(yi−a−b⋅xi)2,

This choice is primarily convenient: the derivative of a quadratic function is a linear function, and linear equations are easily solved. However, further I will indicate other considerations in favor ofSSE ( a , b ) .

GoogleColab.
GitHub
Mathematical analysis
The simplest way to find argmin a , bSSE ( a , b ) - calculate partial derivatives with respect toa andb , equate them to zero and solve the system of linear equations
∂∂ a SSE(a,b)= - 2 N ∑ i = 1 ( y i - a - b x i ) , ∂∂ b SSE(a,b)= - 2 N ∑ i = 1 ( y i - a - b x i ) x i .
0= - 2 N Σ i = 1 ( y i - a - b x i ) , 0= - 2 N Σ i = 1 ( y i - a - b x i ) x i ,
a= ∑ i y iN - b ΣixiN , b= ∑ i x i y iN -∑ixi∑iyiN 2∑ i x 2 iN -( ∑ i x 2 iN )2.
Statistics
The resulting formulas can be compactly written using statistical estimators: mean ⟨ ⋅ ⟩ , variationsσ ⋅ (standard deviation), covarianceσ ( ⋅ , ⋅ ) and correlationsρ ( ⋅ , ⋅ )
a= ⟨ Y ⟩ - b ⟨ x ⟩ , b=⟨xy⟩-⟨x⟩⟨y⟩⟨x2⟩-⟨x⟩2...
ˆb=σ(x,y)σ2x,
ρ(x,y)=σ(x,y)σxσy
ˆb=ρ(x,y)σyσx...

y-⟨y⟩=ρ(x,y)σyσx(x-⟨x⟩)...
- the straight line passes through the center of mass (⟨x⟩,⟨y⟩);
- if along the axis x per unit of length choose σx, and along the axis y - σy, then the slope of the straight line will be from -45∘ before 45∘... This is due to the fact that-1≤ρ(x,y)≤1...
Secondly, now it becomes clear why the regression method is called that way. In units of standard deviationy deviates from its mean by less than x, because |ρ(x,y)|≤1... This is called regression (from the Latin regressus - "return") in relation to the mean. This phenomenon was described by Sir Francis Galton in the late 19th century in his article "Regression to Mediocrity in the Inheritance of Growth." The article shows that traits (such as height) that deviate greatly from the mean are rarely inherited. The characteristics of the offspring seem to tend to the average - nature rests on the children of geniuses.
By squaring the correlation coefficient, we obtain the coefficient of determinationR=ρ2... The square of this statistical measure shows how well the regression model fits the data.R2equal to 1, means that the function fits perfectly to all points - the data is perfectly correlated. It can be proved thatR2shows how much of the variance in the data is due to the best linear model. To understand what this means, we introduce the definitions
Vardata=1N∑i(yi-⟨y⟩)2,Varres=1N∑i(yi-model(xi))2,Varreg=1N∑i(model(xi)-⟨y⟩)2...
Varres - variation of residuals, that is, variation of deviations from the regression model - from yi you need to subtract the model's prediction and find the variation.
Varreg - variation of regression, i.e. variation of the predictions of the regression model at points xi (note that the mean of the model predictions is the same as ⟨y⟩).

Vardata=Varres+Varreg...
σ2data=σ2res+σ2reg...

We strive to get rid of the variability associated with noise and leave only the variability that is explained by the model - we want to separate the wheat from the chaff. The extent to which the best of the linear models succeeded is evidenced byR2equal to one minus the fraction of error variation in the total variation
R2=Vardata-VarresVardata=1-VarresVardata
R2=VarregVardata...
Probability theory
Earlier we came to the loss function SSE(a,b)for reasons of convenience, but it can also be reached using the theory of probability and the method of maximum likelihood (MLM). Let me briefly recall its essence. Suppose we haveNindependent identically distributed random variables (in our case, measurement results). We know the form of the distribution function (for example, the normal distribution), but we want to determine the parameters that are included in it (for exampleμ and σ). To do this, you need to calculate the probability of gettingNdatapoints under the assumption of constant, yet unknown parameters. Due to the independence of the measurements, we get the product of the probabilities of each measurement. If we think of the resulting value as a function of parameters (likelihood function) and find its maximum, we get an estimate of the parameters. Often, instead of the likelihood function, they use its logarithm - it is easier to differentiate it, but the result is the same.
Let's go back to the simple regression problem. Let's say that the valuesx we know exactly, but in measurement ythere is random noise ( weak exogenous property ). Moreover, we assume that all deviations from the straight line ( linearity property ) are caused by noise with a constant distribution ( constant distribution ). Then
y=a+bx+ϵ,
ϵ∼N(0,σ2),p(ϵ)=1√2πσ2e-ϵ22σ2...

Based on the assumptions above, we write down the likelihood function
L(a,b|y)=P(y|a,b)=∏iP(yi|a,b)=∏ip(yi-a-bx|a,b)==∏i1√2πσ2e-(yi-a-bx)22σ2=1√2πσ2e-∑i(yi-a-bx)22σ2==1√2πσ2e-SSE(a,b)2σ2
l(a,b|y)=logL(a,b|y)=-SSE(a,b)+const...
(ˆa,ˆb)=argmaxa,bl(a,b|y)=argmina,bSSE(a,b),
ϵ∼Laplace(0,α),pL(ϵ;μ,α)=α2e-α|ϵ-μ|
ELAD(a,b)=∑i|yi-a-bxi|,
The approach we have used in this section is one possible one. It is possible to achieve the same result using more general properties. In particular, the property of constancy of distribution can be weakened by replacing it with the properties of independence, constancy of variation (homoscedasticity) and absence of multicollinearity. Also, instead of MMP estimation, you can use other methods, for example, linear MMSE estimation.
Multilinear regression
So far, we have considered the regression problem for one scalar feature x, however usually the regressor is n-dimensional vector x... In other words, for each dimension, we registernfeatures, combining them into a vector. In this case, it is logical to accept the model withn+1 independent basis functions of the vector argument - n degrees of freedom correspond n features and one more - regressant y... The simplest choice is linear basis functions(1,x1,⋯,xn)... Whenn=1 we get the already familiar basis (1,x)...
So, we want to find such a vector (set of coefficients)w, what
n∑j=0wjx(i)j=w⊤x(i)≃yi,i=1...N...
ˆw=argminwN∑i=1(yi-w⊤x(i))2
X=(-x(1)⊤-⋯⋯⋯-x(N)⊤-)=(|||x0x1⋯xn|||)=(1x(1)1⋯x(1)n⋯⋯⋯⋯1x(N)1⋯x(N)n)...
Xw≃y...
SSE(w)=‖y-Xw‖2,w∈Rn+1;y∈RN,
ˆw=argminwSSE(w)=argminw(y-Xw)⊤(y-Xw)==argminw(y⊤y-2w⊤X⊤y+w⊤X⊤Xw)...
∂SSE(w)∂w=-2X⊤y+2X⊤Xw,
X⊤Xˆw=X⊤y...
ˆw=(X⊤X)-1X⊤y=X+y,
X+=(X⊤X)-1X⊤
pseudo-inverse to X... The concept of a pseudoinverse matrix was introduced in 1903 by Fredholm, and it played an important role in the works of Moore and Penrose.
Let me remind you what to turnX⊤X and find X+ only possible if the columns Xare linearly independent. However, if the columnsX close to linear dependence, calculation (X⊤X)-1is already becoming numerically unstable. The degree of linear dependence of features inXor, as they say, the multicollinearity of the matrixX⊤X, can be measured by the conditionality number - the ratio of the maximum eigenvalue to the minimum. The bigger it is, the closerX⊤X to degenerate and unstable computation of the pseudoinverse.
Linear algebra
The solution to the problem of multilinear regression can be reached quite naturally with the help of linear algebra and geometry, because even the fact that the norm of the error vector appears in the loss function already hints that the problem has a geometric side. We have seen that an attempt to find a linear model describing the experimental points leads to the equation
Xw≃y...
(|||x0x1⋯xn|||)w=w0x0+w1x1+⋯wnxn...
If in addition to vectorsC(X) we consider all vectors perpendicular to them, then we get one more subspace and we can any vector from RNdecompose into two components, each of which lives in its own subspace. The second, perpendicular space can be characterized as follows (we will need this later). Let it gov∈RNthen
X⊤v=(-x⊤0-⋯⋯⋯-x⊤n-)v=(x⊤0⋅v⋯x⊤n⋅v)

Where ker(X⊤)={v|X⊤v=0}... Each of the subspaces can be reached using the corresponding projection operator, but more on that below.

y=yproj+y⊥,yproj∈C(X),y⊥∈ker(X⊤)...

argminw||y-Xw||=argminw||y⊥+yproj-Xw||=argminw√||y⊥||2+||yproj-Xw||2,
Xˆw=yproj,

X⊤Xw=X⊤yproj=X⊤yproj+X⊤y⊥=X⊤y,
w=(X⊤X)-1X⊤y=X+y,
yproj=Xw=XX+y=ProjXy,
Let's find out the geometric meaning of the coefficient of determination.

y-ˆy⋅1=y-ˉy+ˆy-ˉy⋅1...
‖y-ˆy⋅1‖2=‖y-ˉy‖2+‖ˆy-ˉy⋅1‖2...
Vardata=Varres+Varreg...
R2=VarregVardata,
R=cosθ...
Arbitrary basis
As we know, regression is performed on basis functions fi and its result is the model
f=∑iwifi,
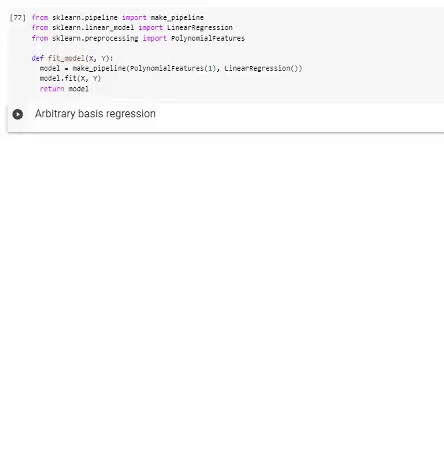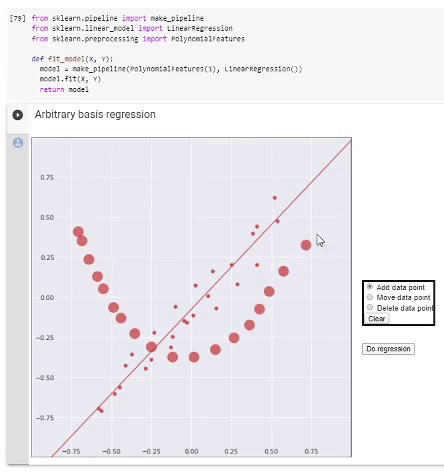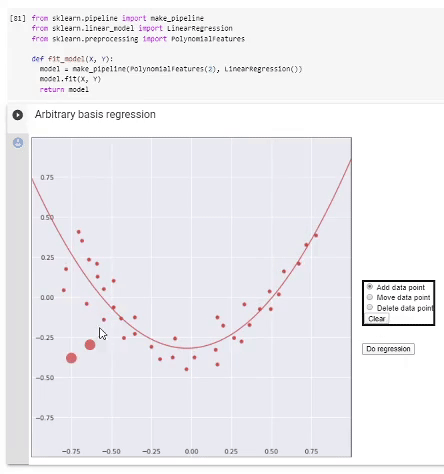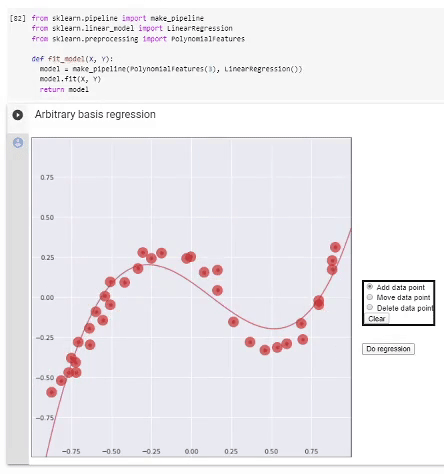
GoogleColab.
GitHub
If we have decided on the basis, then we proceed as follows. We form a matrix of information
Φ=(-f(1)⊤-⋯⋯⋯-f(N)⊤-)=(f0(x(1))f1(x(1))⋯fn(x(1))⋯⋯⋯⋯f0(x(N))f1(x(N))⋯fn(x(N))),
E(w)=‖ϵ(w)‖2=‖y-Φw‖2
ˆw=argminwE(w)=(Φ⊤Φ)-1Φ⊤y=Φ+y
Concluding remarks
Dimension selection problem
In practice, it is often necessary to independently build a model of the phenomenon, that is, to determine how many and which basic functions should be taken. The first impulse to "get more" can play a cruel joke: the model will be too sensitive to noise in the data (overfitting). On the other hand, if you overly restrict the model, it will be too rough (underfitting).
There are two ways to get out of the situation. The first is to consistently increase the number of basic functions, check the quality of the regression and stop in time. Or the second: choose a loss function that will determine the number of degrees of freedom automatically. As a criterion for the success of the regression, you can use the coefficient of determination, which was already mentioned above, however, the problem is thatR2grows monotonically with increasing dimension of the basis. Therefore, the adjusted coefficient is introduced
ˉR2=1-(1-R2)[N-1N-(n+1)],
The second group of approaches is regularization, the most famous of which is Ridge (L2/ ridge / Tikhonov regularization), Lasso (L1regularization) and Elastic Net (Ridge + Lasso). The main idea of these methods is to modify the loss function with additional terms that will not allow the vector of coefficientsw grow indefinitely and thus prevent retraining
ERidge(w)=SSE(w)+α∑i|wi|2=SSE(w)+α‖w‖2L2,ELasso(w)=SSE(w)+β∑i|wi|=SSE(w)+β‖w‖L1,ERU(w)=SSE(w)+α‖w‖2L2+β‖w‖L1,
y=a+bx+ϵ,ϵ∼N(0,σ2),{b∼N(0,τ2)←Ridge,b∼Laplace(0,α)←Lasso...

Numerical methods
Let me say a few words about how to minimize the loss function in practice. SSE is an ordinary quadratic function that is parameterized by the input data, so in principle it can be minimized by the steepest descent method or other optimization methods. Of course, the best results are shown by algorithms that take into account the form of the SSE function, for example, the stochastic gradient descent method. Lasso's implementation of regression in scikit-learn uses the coordinate descent method.
You can also solve normal equations using numerical linear algebra methods. An efficient method that scikit-learn uses for OLS is to find the pseudoinverse using singular value decomposition. The fields of this article are too narrow to touch on this topic, for details I advise you to refer to the course of lectures by K.V. Vorontsov.
Advertising and conclusion
This article is an abridged retelling of one of the chapters of a course on classical machine learning at the Kiev Academic University (successor to the Kiev branch of the Moscow Institute of Physics and Technology, KO MIPT). The author of the article helped create this course. The course is technically done on the Google Colab platform, which allows you to combine LaTeX formatted formulas, Python executable code, and interactive demonstrations in Python + JavaScript, so that students can work with the course materials and run the code from any computer that has a browser. The home page contains links to abstracts, practice workbooks, and additional resources. The course is based on the following principles:
- all materials must be available to students from the first pair;
- the lecture is needed for understanding, not for taking notes (notes are already ready, there is no point in writing them if you don't want to);
- a lecture is more than a lecture (there is more material in the notes than was announced at the lecture, in fact, the notes are a full-fledged textbook);
- visibility and interactivity (illustrations, photos, demos, gifs, code, videos from youtube).
If you want to see the result, take a look at the course page on GitHub .
I hope you were interested, thank you for your attention.