General relativity. Energy as an additional dimension in the Schwarzschild solution

Habritants ! This article describes how to obtain a general metric that includes the Friedman and Schwarzschild metrics as special cases.



To understand the material, you need the concept of derivatives.



Let's imagine that space has a fourth dimension. As if the movement in it took some amount of movement from the object, or vice versa. As if gravity is a purely geometric effect of creating a sub-dimensional vortex around any object with energy.



You have probably stumbled upon a similar visualization of gravity if you are interested in the question:







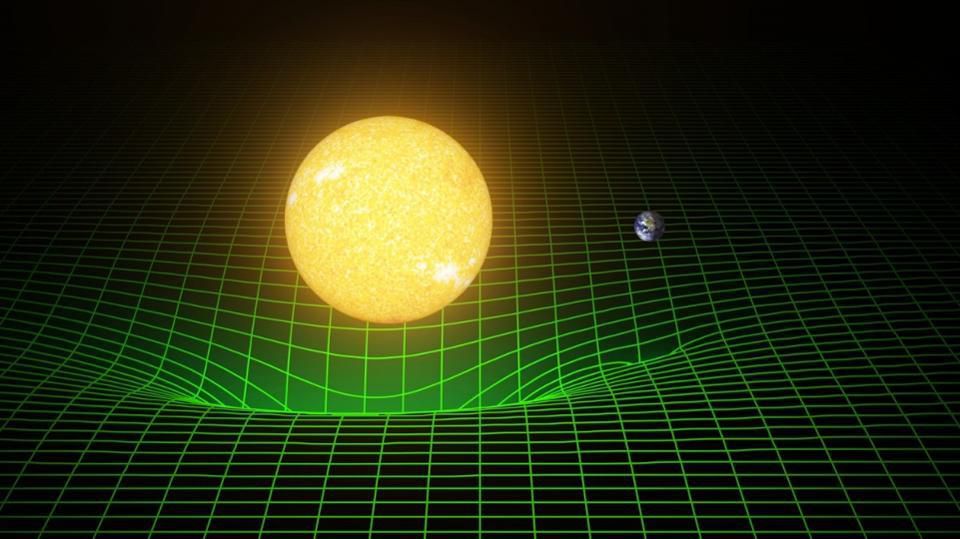
In order to estimate the depth of such a funnel and the mechanism of interaction of objects, we will formulate the expression for the signature interval (1-4).

3-spherical coordinates

Imagine 4-dimensional space $$$\psi (w,x,y,z) = \mathbb{R}^4$ , and define in it the spherical coordinates$$$(r, \theta, \phi, \eta)$ :

$$

$$] \, {w = r\sin\theta\sin\phi\cos\eta; \\ x = r\sin\theta\sin\phi\sin\eta; \\ y = r\sin\theta\cos\phi; \\ z = r\cos\theta } \\$$

To do this, we write down the transition matrix:

$$

$$\vec{r} = \left( \matrix{w \\ x \\ y \\ z} \right) = \left( \matrix{r\sin\theta\sin\phi\cos\eta \\ r\sin\theta\sin\phi\sin\eta \\ r\sin\theta\cos\phi \\ r\cos\theta } \right)$$

Let's calculate the conversion factors:

$$

$$g_r = \left| \frac{\partial\vec{r}}{\partial r} \right| = \sqrt{ \left( \frac{\partial w}{\partial r} \hat{h} + \frac{\partial x}{\partial r} \hat{i} + \frac{\partial y}{\partial r} \hat{j} + \frac{\partial z}{\partial r} \hat{k} \right)^2 } = \\ = \sqrt{sin^2\theta\sin^2\phi\cos^2\eta + \sin^2\theta\sin^2\phi\sin^2\eta + sin^2\theta\cos^2\phi + \cos^2\theta} = 1 \\ g_\theta = \left| \frac{\partial\vec{r}}{\partial \theta} \right| = \sqrt{r^2cos^2\theta\sin^2\phi\cos^2\eta+r^2\cos^2\theta\sin^2\phi\sin^2\eta+r^2\cos^2\theta\cos^2\phi+r^2sin^2\theta} = \\ = \sqrt{r^2(sin^2\theta + \cos^2\theta (cos^2\phi + sin^2\phi (cos^2\eta+sin^2\eta)))} = r \\ g_\phi = \left| \frac{\partial\vec{r}}{\partial \phi} \right| = \sqrt{r^2sin^2\theta\cos^2\phi\cos^2\eta + r^2sin^2\theta\cos^2\phi\sin^2\eta + r^2sin^2\theta\sin^2\phi + 0} = \\ = \sqrt{r^2sin^2\theta} = r\sin\theta \\ g_\eta = \left| \frac{\partial\vec{r}}{\partial \eta} \right| = \sqrt{r^2\sin^2\theta\sin^2\phi\sin^2\eta+r^2\sin^2\theta\sin^2\phi\cos^2\eta} = r\sin\theta\sin\phi$$

And present the corresponding $$$\psi$ interval:

$$

$$ds^2 = \color{red}{(-1)\cdot dt^2} + (dw^2 + \color{green}{ dx^2 + dy^2 + dz^2}) \\ ds^2 = (-1)\cdot dt^2 + (g_r^2 dr^2 + g_\theta^2 d\theta^2 + g_\phi^2 d\phi^2 + g_\eta^2 d\eta^2) \\ ds^2 = (-1)\cdot dt^2 + 1 \cdot dr^2 + r^2 \cdot d\theta^2 + r^2 \cdot \sin^2\theta \cdot d\phi^2 + r^2 \cdot \sin^2\theta \cdot \sin^2\phi \cdot d\eta^2 \\ ds^2 = \color{red}{(-1)\cdot dt^2} + \color{magenta}{1 \cdot dr^2} + \color{green}{r^2 \left( d\theta^2 + \sin^2\theta \cdot d\phi^2 + \sin^2\theta \cdot \sin^2\phi \cdot d\eta^2 \right)}$$

Red - temporal component, presented similarly to the FLRW metric.

Green - the spatial component, represented similarly to the FLRW metric, and representing the surface of a 3-sphere.



Magenta turned out to be a link suspended between time and space - the differential of the multiplier change of the spatial part.

General view of the interval

Continuing the development of the ideas outlined in the previous article , we put the change in the fourth dimension as a measure related to the relative amount of energy of objects, therefore, we supplement the metric of the component$$$\color{orange}{-dr^2}$due to consideration of an energetically closed system, which will be assumed to be true both for the Universe as a whole (Friedmann's solution) and for a spherically symmetric massive body (Schwarzschild's solution). The reader who disagrees with this interpretation may simply consider it a mathematical trick:

$$

$$ds^2 = \color{red}{(-1)\cdot dt^2 \left( 1 - \color{magenta}{\frac{dr^2}{dt^2}} \right)} + \color{green}{r^2 \left( d\theta^2 + \sin^2\theta \cdot d\phi^2 + \sin^2\theta \cdot \sin^2\phi \cdot d\eta^2 - \color{orange}{\frac{dr^2}{r^2}} \right)}$$

Magenta in the temporal part is clear:

$$

$$\color{magenta}{ \frac{dr^2}{dt^2} = \dot{r}^2 }$$

Work on bugs. Unfortunately, present$$$\psi'(\theta, \phi, \eta) = \mathbb{R}^3 \in \psi$flat through coordinate transformation is not possible. If you bring it to mind$$$r^2 \cdot (dx^2 + dy^2 + dz^2)$the basis vectors are no longer orthogonal to each other.

Further considerations can be valid only for the case of approximation$$$\sin^2 \theta = \rho^2$ acceptable for large values $$$r$...

Reform the green one to show that the space $$$\psi'(\theta, \phi, \eta) = \mathbb{R}^3 \in \psi$ can be represented in angular coordinates $$$(x_1, y_1, z_1)$ like the FLRW metric:

$$

$$\color{green}{r^2 \left( d\theta^2 + \sin^2\theta \cdot d\phi^2 + \sin^2\theta \cdot \sin^2\phi \cdot d\eta^2 - \color{orange}{\frac{dr^2}{r^2}} \right) = \\ = r^2 \cdot dx_1^2 + r^2 \cdot \sin^2\theta \cdot \frac{d\phi^2}{d\theta^2} \cdot dy_1^2 + r^2 \cdot \sin^2\theta \cdot \sin^2\phi \cdot \frac{d\eta^2}{d\theta^2} \cdot dz_1^2 - \color{orange}{dr^2} =} \quad \rightarrow (1)$$

In this case, the transition coefficients are equal:

$$

$$dx_1^2 = d\theta^2; \\ dy_1^2 = \sin^2 \theta \cdot d\phi^2 = \sin^2 \theta \cdot \frac{d\phi^2}{d\theta^2} \cdot d\theta^2 = \sin^2 \theta \cdot \left( \frac{d\phi}{d\vec{r}} \cdot \frac{d\vec{r}}{d\theta} \right)^2 \cdot d\theta^2 = \\ = \sin^2\theta \cdot \left( \frac{g_\theta}{g_\phi} \right)^2 \cdot d\theta^2 = \frac{\sin^2\theta}{\sin^2\theta} \cdot d\theta^2 = d\theta^2; \\ \frac{d\eta^2}{d\theta^2} = \frac{g_\theta^2}{g_\eta^2} = \frac{1}{\sin^2\theta \cdot \sin^2\phi };$$

Therefore, taking into account the basis vectors:

$$

$$(1) \rightarrow \quad \color{green}{= r^2 \cdot dx_1^2 \cdot \vec{e_{\theta}}^2 + r^2 \cdot dy_1^2 \cdot \vec{e_{\phi}}^2 + r^2 \cdot dz_1^2 \cdot \vec{e_{\eta}}^2 - \color{orange}{dr^2 \cdot \vec{e_r}^2} = } \quad \rightarrow \ (2)$$

what is 3-space $$$\psi'_1(x_1, y_1, z_1)$ with linear $$$d\theta$ basis vectors, scale factor $$$r$ and instantaneous length $$$dl^2 = dx_1^2 + dy_1^2 + dz_1^2$, in our case, collectively reduced by the value $$$dr^2/r^2$:

$$

$$(2) \rightarrow \quad \color{green}{ = r^2 \cdot \left( dx_1^2 \cdot \vec{e_\theta}^2 + dy_1^2 \cdot \vec{e_\phi}^2 + dz_1^2 \cdot \vec{e_\eta}^2 - \color{orange}{\frac{dr^2}{r^2} \cdot \vec{e_r}^2} \right) = } \quad \rightarrow \ (3)$$

Without the orange component, we got the spatial part of the interval of the standard cosmological model for “flat” space with a possible degradation of the spatial scale factor $$$r$in time, as in FLRW.



"Pack" extra$$$dr^2$ will be more practical again in spherical, only now usual for a three-dimensional sphere $$$(x_1, y_1, z_1) \rightarrow(\rho, \varphi, \zeta)$... To distinguish between coordinates for 3-spherical and 2-spherical systems, the latter are denoted$$$(\rho, \varphi, \zeta)$:

$$

$$(3) \rightarrow \quad \color{green}{ r^2 \cdot \left( dx_1^2 + dy_1^2 +dz_1^2 - \color{orange}{\frac{dr^2}{r^2}} \right) = r^2 \cdot \left( d\rho^2 - \color{orange}{\frac{dr^2}{r^2}} + \rho^2 \cdot d\varphi^2 + \rho^2 \cdot \sin^2 \varphi \cdot d\zeta^2 \right) = \\ = r^2 \cdot \left( \left(1 - \color{orange}{\frac{d(\ln r)^2}{d\rho^2}} \right) d\rho^2 + \rho^2 \cdot ( d\varphi^2 + \sin^2 \varphi \cdot d\zeta^2) \right) }$$

where the order of magnitude ratio $$$dr = r d\rho \ \Rightarrow r = e^\rho$, and $$$\varphi, \zeta$ by the tangent theorem:

$$

$${ d\varphi = \frac{r}{\rho} \cdot d\phi; \\ d\zeta = \frac{r \cdot \sin \phi}{\rho \cdot \sin\varphi} \cdot d\eta. }$$

Then the full interval will be:

$$

$$ds^2 = \color{red}{(-1)\cdot dt^2 \left( 1 - \color{magenta}{\frac{dr^2}{dt^2}} \right)} + \color{green}{ r^2 \cdot \left( \left(1 - \color{orange}{\frac{d(\ln r)^2}{d\rho^2}} \right) d\rho^2 + \rho^2 \cdot ( d\varphi^2 + \sin^2 \varphi \cdot d\zeta^2) \right)} \qquad (A)$$

The result is a combined interval, as if "cobbled together" from the form of an interval of the FLRW metric and the Schwarzschild metric, each of which represents a particular case of physical interactions. Now let's see how from$$$(A)$ corresponding solutions are obtained.

Interval view for the Friedman metric

Purely mathematically, an interval of the form $$$(A)$ becomes the FLRW metric of the standard cosmological model by simply excluding the energy component $$$dr = 0$:

$$

$$ds^2 = \color{red}{(-1)\cdot dt^2} + \color{green}{ r^2 \cdot \left( d\rho^2 + \rho^2 \cdot ( d\varphi^2 + \sin^2 \varphi \cdot d\zeta^2) \right)}$$

Which, as shown above, can also be rewritten like this:

$$

$$ds^2 = \color{red}{(-1)\cdot dt^2} + \color{green}{ r^2 \cdot \left( dx^2 + dy^2 + dz^2 \right)}$$

The solution of the equations of general relativity for such an interval gives the dependence $$$r \propto t^{2/3}$...



However, the empirical QCS data for objects$$$z>0.3$show the consolidated deviation from this relationship.



Possibly a solution for an interval like$$$(A)$ will give a more accurate relationship, but I haven't found it yet.

General relativity solution in terms of the Schwarzschild metric

Let us compare the resulting interval with the Schwarzschild metric :

$$

$$ds^2 = -\color{red}{(1-\frac{\rho_s}{\rho})} \cdot dt^2 + \color{orange}{\frac{1}{1 - \frac{\rho_s}{\rho}}} \cdot d\rho^2 + \rho^2 \cdot d\phi^2 + \rho^2 \sin^2 \phi \cdot d\zeta^2$$

If we imagine a system of interacting objects on a low-energy scale $$$(dr/r \rightarrow \infty)$then $$$r$ can be taken to be equal to one without losing mathematical connectivity, the space will then become pseudo-Euclidean, and the interval $$$(A)$ can be rewritten as follows:

$$

$$ds^2 = (-1)\cdot \color{red}{ \left( 1 - \frac{dr^2}{dt^2} \right) } \cdot dt^2 + \color{orange}{ \left(1 - \frac{dr^2}{d\rho^2} \right) } \cdot d\rho^2 + \rho^2 \cdot ( d\varphi^2 + \sin^2 \varphi \cdot d\zeta^2)$$

Mathematically, this is exactly the same as if we performed a trick $$$\pm dr^2$ for empty 3-space in spherical coordinates $$$(\rho, \varphi, \zeta)$...



That is, for the flat vacuum case, the interval$$$(A)$will have a solution similar to the solution of the Schwarzschild metric, provided that the factors highlighted in red and orange are equivalent. We get the system:

$$

$$1-\frac{\rho_s}{\rho} = 1 - \frac{dr^2}{dt^2}; \\ \frac{1}{1 - \frac{\rho_s}{\rho}} = 1 - \frac{dr^2}{d\rho^2}.$$

Where $$$t, r, \rho$- in order: time, curvature (energy), radius (distance) in a spherically symmetric gravitational field along the zero total curvature of space.

Using simple mathematical transformations, we get a very laconic solution:

$$

$$-dt^2 + dr^2 - d\rho^2 = 0,$$

which confirms that:

1. The fourth coordinate is linear to the radial coordinate.
2. The fourth coordinate is the imaginary axis coordinate.

The first, in my opinion, is very important because it shows that the energy presented as an additional axis is almost isotropic to the observables. Second, it allows you to understand why she manifests herself differently. And "unobservable".



In addition, I would like to note that the very setting in the energy interval with a negative sign with respect to space and positive with respect to time allows us to formulate their relationship as follows: space is energy-time, it is overcome in energy-time.

Summary

It seems to me that the continuation of the course on the geometrization of physics shows itself to be a very promising direction. The imaginary energy axis in cosmology could serve as a springboard to Maxwell's equations.

Marginal notes. Looking ahead, I will allow myself to assume that one imaginary measurement for organizing the mechanisms of charge and mass will not be enough. Plus electro-magnetic dualism as an argument in favor of at least two dimensions. And some symmetry in the form: time dimension + two energetic = three space.

When going to micro-scale I will try to move in the direction of "splitting"$$$r$:

$$

$$ds^2 = - dt^2 - dv^2 - dw^2 + dx^2 + dy^2 + dz^2$$

Remark 08/23/2020:

Additional axis imaginary $$$r$ was originally given by the sign with which $$$\pm dr^2$were divided into temporal and spatial components. That is, if we imagine the gravitational field not as a funnel, but as a hill, then the fourth dimension will turn out to be co-directed to space:

$$

$$dt^2 + dr^2 + d\rho^2 = 0$$

Such indifference of the properties shown in (1,3) from the direction of the fifth axis, apparently, is a sign of its closed form.