Inventing a bicycle or writing a perceptron in C ++. Part 3

Let's implement training a multilayer perceptron in C ++ using the backpropagation method.

Foreword

Hello everyone!) Before we get down to the basis of this article, I would like to say a few words about the previous parts. The implementation I proposed is a mockery of the computer's RAM, tk. the three-dimensional vector rapes memory with an abundance of empty cells, for which memory is also reserved. Therefore, the method is far from the best, but I hope it will help beginner programmers in this area understand what is “under the hood” of the simplest neural networks. This time. In describing the activation function in the first part, I made a mistake - the activation function does not have to be limited in the range of values. It all depends on the goals of the programmer. The only condition is that the function must be defined on the entire number axis. It is two

Introduction

-, . backpropagation — . , !

: habr.com/ru/post/514372

backpropagation — .

, , , .

:

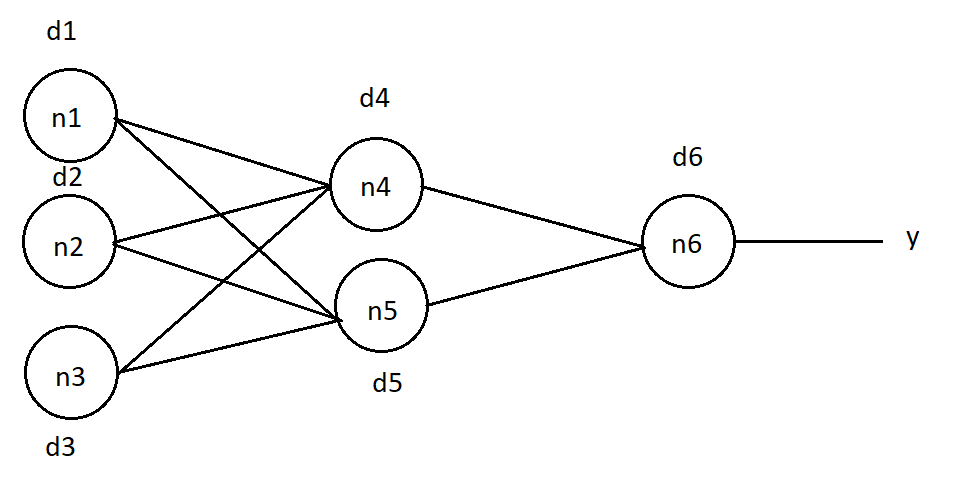
, , . , , . , , . : $$$d j ​ =f(net j ​ )(1−f(net j ​ )) k ∑ ​ d k ​ w kj ​$ (1), j — , , k — , , .. .

, . "O". n6 d6 = (O — y)*( f(in) )*(1 — f(in) ) (2), in —

n6, f(in) — .

(1), . n4 :

d4 = d6 * w46 *( f(in4) ) * (1 — f(in4)), w46 — n4 n6, in4 — n4.

d5 = d6 * w56 *( f(in5) ) * (1 — f(in5)), n5.

d1 = (d4 * w14 + d5 * w15) *( f(in1) ) * (1 — f(in1)), n1, , — .

n2 n3 :

d2 = (d4 * w24 + d5 * w25) *( f(in2) ) * (1 — f(in2))

d3 = (d4 * w34 + d5 * w35) *( f(in3) ) * (1 — f(in3))

, , :

Δw46 = d6 * A * f(in4), w46 — n4 n6 , f(in4) — n4, A — , — , .

Δw56 = d6 * A * f(in5), n5 n6.

:

Δw14 = d4 * A * f(in1)

Δw24 = d4 * A * f(in2)

Δw34 = d4 * A * f(in3)

Δw15 = d4 * A * f(in1)

Δw25 = d4 * A * f(in2)

Δw35 = d4 * A * f(in3)

? . .

void NeuralNet::learnBackpropagation(double* data, double* ans, double acs, double k) {  //data -   , ans -     , k -   , acs-  

, - :

for (uint32_t e = 0; e < k; e++) {
		double* errors = new double[neuronsInLayers[numLayers - 1]]; //      
                // "Do_it"    "Forward"
		Forward(neuronsInLayers[0], data);//    
		getResult(neuronsInLayers[numLayers - 1], errors);//     

:

for (uint16_t n = 0; n < neuronsInLayers[numLayers - 1]; n++) {
			neurons[n][2][numLayers - 1] = (ans[n] - neurons[n][1][numLayers - 1]) * (neurons[n][1][numLayers - 1]) * (1 - neurons[n][1][numLayers - 1]);
		}

, :

for (uint8_t L = numLayers - 2; L > 0; L--) {
			for (uint16_t neu = 0; neu < neuronsInLayers[L]; neu++) {
				for (uint16_t lastN = 0; lastN < neuronsInLayers[L + 1]; lastN++) {
					neurons[neu][2][L] += neurons[lastN][2][L + 1] * weights[neu][lastN][L] * neurons[neu][1][L] * (1 - neurons[neu][1][L]);
					weights[neu][lastN][L] += neurons[neu][1][L] * neurons[lastN][2][L + 1] * acs;
				}
			}
		}

:

void NeuralNet::learnBackpropagation(double* data, double* ans, double acs, double k) {  //k -    acs-  
	for (uint32_t e = 0; e < k; e++) {
		double* errors = new double[neuronsInLayers[numLayers - 1]];
		Forward(neuronsInLayers[0], data);
		getResult(neuronsInLayers[numLayers - 1], errors);
		for (uint16_t n = 0; n < neuronsInLayers[numLayers - 1]; n++) {
			neurons[n][2][numLayers - 1] = (ans[n] - neurons[n][1][numLayers - 1]) * (neurons[n][1][numLayers - 1]) * (1 - neurons[n][1][numLayers - 1]);
		}
		for (uint8_t L = numLayers - 2; L > 0; L--) {
			for (uint16_t neu = 0; neu < neuronsInLayers[L]; neu++) {
				for (uint16_t lastN = 0; lastN < neuronsInLayers[L + 1]; lastN++) {
					neurons[neu][2][L] += neurons[lastN][2][L + 1] * weights[neu][lastN][L] * neurons[neu][1][L] * (1 - neurons[neu][1][L]);
					weights[neu][lastN][L] += neurons[neu][1][L] * neurons[lastN][2][L + 1] * acs;
				}
			}
		}
	}
}

. :

#include <stdio.h>
#include "neuro.h"
int main()
{
    
    uint16_t neurons[3] = {16, 32, 10}; //        , -       
/*        ""  
        
*/
    NeuralNet net(3, neurons);
    double teach[4 * 4] = {//  ""  "4"  , - : 4*4 = 16
        1,0,1,0,
        1,1,1,0,
        0,0,1,0,
        0,0,1,0,
    };
    double test[4 * 4] = {//  "4",  -
        1,0,0,1,
        1,1,1,1,
        0,0,0,1,
        0,0,0,1,
    };
    double ans[10] = {0, 0, 0, 0, 1, 0, 0, 0, 0, 0,};//       , "1"    ,       "4"
    double output[10] = { 0 };//      
    net.Forward(4*4, teach); //    
    net.getResult(10, output); 
    for (uint8_t i = 0; i < 10; i++) printf("%d: %f \n", i, output[i]*100); //  
    net.learnBackpropagation(teach, ans, 0.50, 1000); //    "test",  : 0.5
    printf("\n");
    net.Forward(4 * 4, test);//     
    net.getResult(10, output);
    for (uint8_t i = 0; i < 10; i++) printf("%d: %f \n", i, output[i]*100);
    return 0;
}

:

( ), , 0 9. . , «4»

, , - , . . . , , .

...

. , .

Thank you for the attention paid to this article and for the comments on the previous publication. I will duplicate the link to the library files .

Leave your comments, suggestions. See you later!