Hello, Habr.
In this article, I would like to touch upon the topic of the application of information technology in the Earth Sciences, namely, in Hydrology and Cartography. Below the cut is a description of the stream ranking algorithm and the plug-in we have implemented for the open geographic information system QGIS.
Introduction
Currently, an important aspect of hydrological research is not only field observations, but also office work with hydrological data, including using GIS (geographic information systems). However, studying the spatial structure of hydrological systems can be difficult due to the large amount of data. In such cases, you cannot do without the use of additional tools that allow a specialist to automate the process.
An important role in working with digital data in general and hydrological data in particular is played by visualization - the correct and visual presentation of the analysis results. To display watercourses in classical cartography, the following method is adopted: rivers are depicted by a solid line with a gradual (depending on the number of tributaries flowing into the river) thickening from the source to the mouth. In addition, for the segments of the river network, some ranking is often necessary according to the degree of distance from the source. Information of this kind is important not only from the point of view of visualization, but also suitable for a more complete perception of the data structure, their spatial distribution, and correct subsequent processing.
The task of ranking watercourses can be illustrated as follows (Fig. 1):

Figure 1. The task of ranking watercourses, numbers indicate the attribute of the total number of inflowing tributaries assigned to each segment of the river network
Thus, each segment of the river needs to be associated with a value that would show how many segments collectively flow into the given section.
, ArcGIS open-source QGIS, . , , , , . , - . , , , (OpenStreetMap, Natural Earth, ).
, , , .
— . QGIS — "Lines Ranking". QGIS, GitHub.
For the plugin to work, the QGIS version> = 3.14 is required, as well as the following dependencies: Python programming language libraries - networkx and pandas.
, (Line, MultiLine). , .
- “fid”. GRASS — v.clean — , .
(Start Point Coordinates), . , , , QGIS. , ( ).
: , , .
: . — , . , , . , , . . .
— , , .
, . / , .. , .. (. 2), , ..
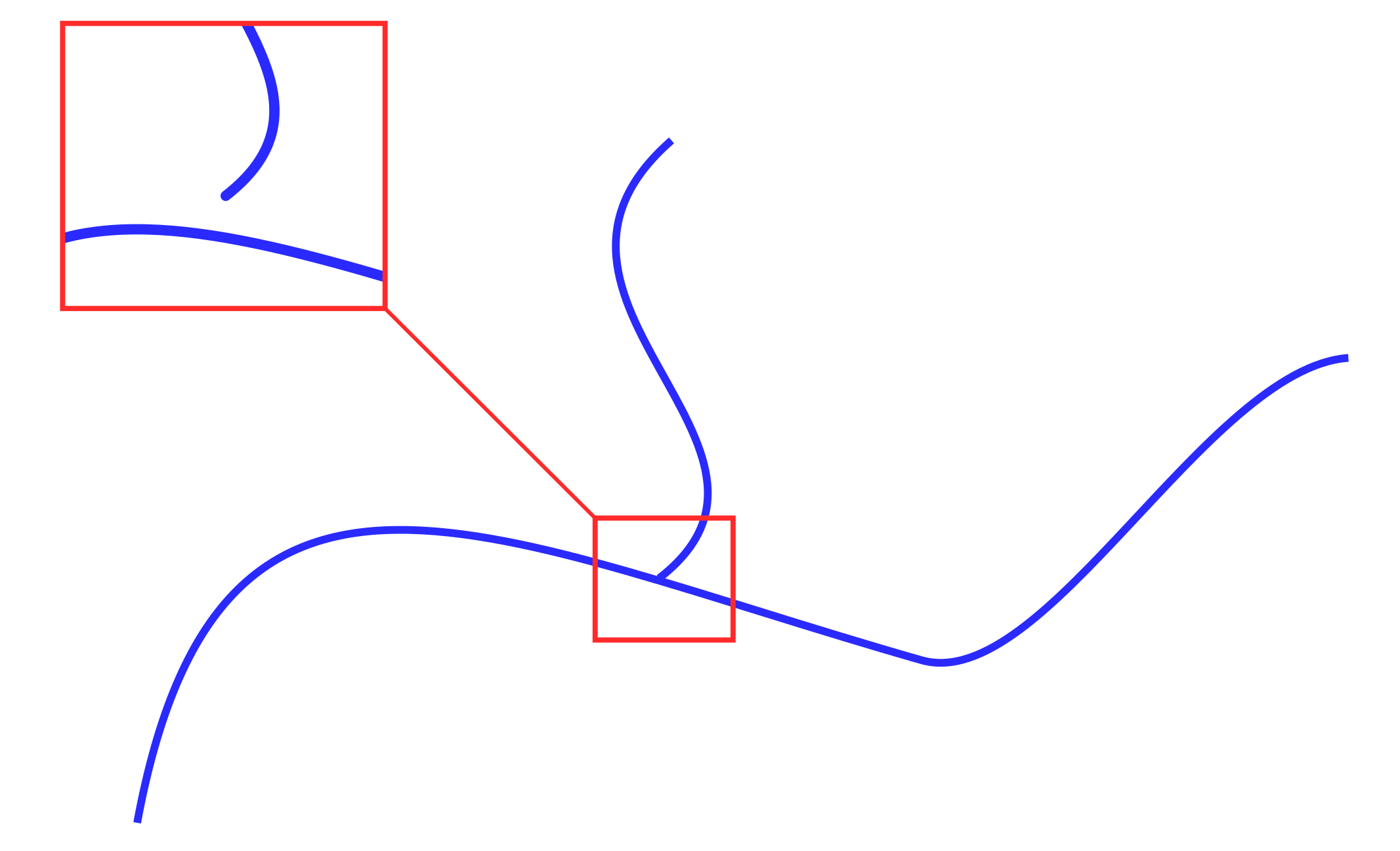
2.
: ““ , . QGIS – “ ” (fixgeometries — ) v.clean ( GRASS).
, . (. 3).

3.
, QGIS " " (splitwithlines — ) .
QGIS (. 4). ( -> -> -> ).

4.
" " (lineintersections — ) , . .
(. 5).

5.
Python networkx. , — , ( ), .
, , , ( ). , , "" (). :
- "rank" ( ) "offspring" ( );
- "value" "distance" ( ).
, , .
"rank" "offspring"
— . , "rank" . , , , , . ( )

? , , .
: - ( ), . (. 6).

6.
, 1 , — .
— ? — , , , — ( , , , ). A* (A-star), , . ( ).
1) . . . (. 7)

7.
, "length", . , .
Input:
- G —
- start — ,
- dataframe — pandas , 2 : id_field ( /) 'length' ( )
- id_field — dataframe,
- main_id — , ( = None)
Output:
- , 1, : 2 3, 'length' 1 — 10, 2 — 15, 3 — 20. : (1, 2) (2, 1) — 15; (1, 3) (3, 1) — 20 ..
- last_vertex — ( )
# Function for assigning weights to graph edges
def distance_attr(G, start, dataframe, id_field, main_id = None):
# List of all vertexes that can be reached from the start vertex using BFS
vert_list = list(nx.bfs_successors(G, source=start))
# One of the most remote vertices in the graph (this will be necessary for A*)
last_vertex = vert_list[-1][-1][0]
for component in vert_list:
vertex = component[0] # The vertex where we are at this iteration
neighbors = component[1] # Vertices that are neighboring (which we haven't visited yet)
dist_vertex = int(dataframe['length'][dataframe[id_field] == vertex])
# Assign the segment length value as a vertex attribute
attrs = {vertex: {'component' : 1, 'size' : dist_vertex}}
nx.set_node_attributes(G, attrs)
for n in neighbors:
# If the main index value is not set
if main_id == None:
# Assign weights to the edges of the graph
# The length of the section in meters (int)
dist_n = int(dataframe['length'][dataframe[id_field] == n])
# Otherwise we are dealing with a complex composite index
else:
# If the vertex we are at is part of the main river
if vertex.split(':')[0] == main_id:
# And at the same time, the vertex that we "look" at from the vertex "vertex" also, then
if n.split(':')[0] == main_id:
# The weight value must be zero
dist_n = 0
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
attrs = {(vertex, n): {'weight': dist_n},
(n, vertex): {'weight': dist_n}}
nx.set_edge_attributes(G, attrs)
# Assign attributes to the nodes of the graph
attrs = {n: {'component' : 1, 'size' : dist_n}}
nx.set_node_attributes(G, attrs)
# Look at the surroundings of the vertex where we are located
offspring = list(nx.bfs_successors(G, source = vertex, depth_limit = 1))
offspring = offspring[0][1]
# If the weight value was not assigned, we assign it
for n in offspring:
if len(G.get_edge_data(vertex, n)) == 0:
##############################
# Assigning weights to edges #
##############################
if main_id == None:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
if vertex.split(':')[0] == main_id:
if n.split(':')[0] == main_id:
dist_n = 0
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
attrs = {(vertex, n): {'weight': dist_n},
(n, vertex): {'weight': dist_n}}
nx.set_edge_attributes(G, attrs)
##############################
# Assigning weights to edges #
##############################
elif len(G.get_edge_data(n, vertex)) == 0:
##############################
# Assigning weights to edges #
##############################
if main_id == None:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
if vertex.split(':')[0] == main_id:
if n.split(':')[0] == main_id:
dist_n = 0
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
attrs = {(vertex, n): {'weight': dist_n},
(n, vertex): {'weight': dist_n}}
nx.set_edge_attributes(G, attrs)
##############################
# Assigning weights to edges #
##############################
for vertex in list(G.nodes()):
# If the graph is incompletely connected, then we delete the elements that we can't get to
if G.nodes[vertex].get('component') == None:
G.remove_node(vertex)
else:
pass
return(last_vertex)
# The application of the algorithm
last_vertex = distance_attr(G, '7126:23', dataframe, id_field = 'id', main_id = '7126')2) A* (-star) ( ). "";
3) . , , 1, — 2, — 3 ..
4) . , , , .
Input:
- G —
- start — ,
- last_vertex —
Output:
- . 1 , . 2 , 1. 3 , 2 .. , 'rank', 'offspring'. 'offspring' ' , '.
# Function for assigning 'rank' and 'offspring' attributes to graph vertices
def rank_set(G, start, last_vertex):
# Traversing a graph with attribute assignment
# G --- graph as a networkx object
# vertex --- vertex from which the graph search begins
# kernel_path --- list of vertexes that are part of the main path that the search is being built from
def bfs_attributes(G, vertex, kernel_path):
# Creating a copy of the graph
G_copy = G.copy()
# Deleting all edges that are associated with the reference vertexes
for kernel_vertex in kernel_path:
# Leaving the reference vertex from which we start the crawl
if kernel_vertex == vertex:
pass
else:
# For all other vertexes, we delete edges
kernel_n = list(nx.bfs_successors(G_copy, source = kernel_vertex, depth_limit = 1))
kernel_n = kernel_n[0][1]
for i in kernel_n:
try:
G_copy.remove_edge(i, kernel_vertex)
except Exception:
pass
# The obtained subgraph is isolated from all reference vertices, except the one
# from which the search begins at this iteration
# Breadth-first search
all_neighbors = list(nx.bfs_successors(G_copy, source = vertex))
# Attention!
# Labels are not assigned on an isolated subgraph, but on the source graph
for component in all_neighbors:
v = component[0] # The vertex where we are at this iteration
neighbors = component[1] # Vertices that are neighboring (which we haven't visited yet)
# Value of the 'rank' attribute in the considering vertex
att = G.nodes[v].get('rank')
if att != None:
# The value of the attribute to be assigned to neighboring vertices
att_number = att + 1
# We look at all the closest first offspring
first_n = list(nx.bfs_successors(G, source = v, depth_limit = 1))
first_n = first_n[0][1]
# Assigning ranks to vertices
for i in first_n:
# If the neighboring vertex is the main node in this iteration, then skip it
# vertex - the reference point from which we started the search
if i == vertex:
pass
else:
current_i_rank = G.nodes[i].get('rank')
# If the rank value has not yet been assigned, then assign it
if current_i_rank == None:
attrs = {i: {'rank': att_number}}
nx.set_node_attributes(G, attrs)
# If the rank in this node is already assigned
else:
# The algorithm either "looks back" at vertices that it has already visited
# In this case we don't do anything
# Either the algorithm "came up" to the main path (kernel path) in the graph
if any(i == bearing_v for bearing_v in kernel_path):
G.remove_edge(v, i)
else:
pass
# Additional "search"
for neighbor in neighbors:
# We look at all the closest first offspring
first_n = list(nx.bfs_successors(G, source = neighbor, depth_limit = 1))
first_n = first_n[0][1]
for i in first_n:
# If the neighboring vertex is the main node in this iteration, then skip it
# vertex - the reference point from which we started the search
if i == vertex:
pass
else:
# The algorithm either "looks back" at vertices that it has already visited
# In this case we don't do anything
# Either the algorithm "came up" to the main path (kernel path) in the graph
if any(i == bearing_v for bearing_v in kernel_path):
G.remove_edge(neighbor, i)
else:
pass
# Finding the shortest path A* - building a route around which we will build the next searchs
a_path = list(nx.astar_path(G, source = start, target = last_vertex, weight = 'weight'))
##############################
# Route validation block #
##############################
true_a_path = []
for index, V in enumerate(a_path):
if index == 0:
true_a_path.append(V)
elif index == (len(a_path) - 1):
true_a_path.append(V)
else:
# Previous and next vertices for the reference path (a_path)
V_prev = a_path[index - 1]
V_next = a_path[index + 1]
# Which vertexes are adjacent to this one
V_prev_neighborhood = list(nx.bfs_successors(G, source = V_prev, depth_limit = 1))
V_prev_neighborhood = V_prev_neighborhood[0][1]
V_next_neighborhood = list(nx.bfs_successors(G, source = V_next, depth_limit = 1))
V_next_neighborhood = V_next_neighborhood[0][1]
# If the next and previous vertices are connected to each other without an intermediary
# in the form of vertex V, then vertex V is excluded from the reference path
if any(V_next == VPREV for VPREV in V_prev_neighborhood):
if any(V_prev == VNEXT for VNEXT in V_next_neighborhood):
pass
else:
true_a_path.append(V)
else:
true_a_path.append(V)
##############################
# Route validation block #
##############################
# Verification completed
a_path = true_a_path
RANK = 1
for v in a_path:
# Assign the attribute rank value - 1 to the starting vertex. The further away, the greater the value
attrs = {v: {'rank' : RANK}}
nx.set_node_attributes(G, attrs)
RANK += 1
# The main route is ready, then we will iteratively move from each node
for index, vertex in enumerate(a_path):
# Starting vertex
if index == 0:
next_vertex = a_path[index + 1]
# Disconnect vertices
G.remove_edge(vertex, next_vertex)
# Subgraph BFS block
bfs_attributes(G, vertex = vertex, kernel_path = a_path)
# Connect vertices back
G.add_edge(vertex, next_vertex)
# Finishing vertex
elif index == (len(a_path) - 1):
prev_vertex = a_path[index - 1]
# Disconnect vertices
G.remove_edge(prev_vertex, vertex)
# Subgraph BFS block
bfs_attributes(G, vertex = vertex, kernel_path = a_path)
# Connect vertices back
G.add_edge(prev_vertex, vertex)
# Vertices that are not the first or last in the reference path
else:
prev_vertex = a_path[index - 1]
next_vertex = a_path[index + 1]
# Disconnect vertices
# Previous with current vertex
try:
G.remove_edge(prev_vertex, vertex)
except Exception:
pass
# Current with next vertex
try:
G.remove_edge(vertex, next_vertex)
except Exception:
pass
# Subgraph BFS block
bfs_attributes(G, vertex = vertex, kernel_path = a_path)
# Connect vertices back
try:
G.add_edge(prev_vertex, vertex)
G.add_edge(vertex, next_vertex)
except Exception:
pass
# Attribute assignment block - number of descendants
vert_list = list(nx.bfs_successors(G, source = start))
for component in vert_list:
vertex = component[0] # The vertex where we are at this iteration
neighbors = component[1] # Vertices that are neighboring (which we haven't visited yet)
# Adding an attribute - the number of descendants of this vertex
n_offspring = len(neighbors)
attrs = {vertex: {'offspring' : n_offspring}}
nx.set_node_attributes(G, attrs):

, , . .
, "" , , , , , .
"value" "distance"
, "rank" "offspring". .
, , , , "value" — 1. , , "value", 1, "value" ( 1 , ) "value". , , .
, .
Input:
- G — 'rank' 'offspring'
- start — ,
Output:
- G 'value'. ' '. 'distance', , , .
# Function for determining the order of river segments similar to the Shreve method
# In addition, the "distance" attribute is assigned
def set_values(G, start, considering_rank, vert_list):
# For each vertex in the list
for vertex in vert_list:
# If value has already been assigned, then skip it
if G.nodes[vertex].get('value') == 1:
pass
else:
# Defining descendants
offspring = list(nx.bfs_successors(G, source = vertex, depth_limit = 1))
# We use only the nearest neighbors to this vertex (first descendants)
offspring = offspring[0][1]
# The cycle of determining the values at the vertices of a descendant
last_values = []
for child in offspring:
# We only need descendants whose rank value is greater than that of the vertex
if G.nodes[child].get('rank') > considering_rank:
if G.nodes[child].get('value') != None:
last_values.append(G.nodes[child].get('value'))
else:
pass
else:
pass
last_values = np.array(last_values)
sum_values = np.sum(last_values)
# If the amount is not equal to 0, the attribute is assigned
if sum_values != 0:
attrs = {vertex: {'value' : sum_values}}
nx.set_node_attributes(G, attrs)
else:
pass
# Function for iteratively assigning the value attribute
def iter_set_values(G, start):
# Vertices and corresponding attribute values
ranks_list = []
vertices_list = []
offspring_list = []
for vertex in list(G.nodes()):
ranks_list.append(G.nodes[vertex].get('rank'))
vertices_list.append(vertex)
att_offspring = G.nodes[vertex].get('offspring')
if att_offspring == None:
offspring_list.append(0)
else:
offspring_list.append(att_offspring)
# Largest rank value in a graph
max_rank = max(ranks_list)
# Creating pandas dataframe
df = pd.DataFrame({'ranks': ranks_list,
'vertices': vertices_list,
'offspring': offspring_list})
# We assign value = 1 to all vertices of the graph that have no offspring
value_1_list = list(df['vertices'][df['offspring'] == 0])
for vertex in value_1_list:
attrs = {vertex: {'value' : 1}}
nx.set_node_attributes(G, attrs)
# For each rank, we begin to assign attributes
for considering_rank in range(max_rank, 0, -1):
# List of vertices of suitable rank
vert_list = list(df['vertices'][df['ranks'] == considering_rank])
set_values(G, start, considering_rank, vert_list)
# Assigning the "distance" attribute to the graph vertices
# List of all vertexes that can be reached from the start vertex using BFS
vert_list = list(nx.bfs_successors(G, source = start))
for component in vert_list:
vertex = component[0] # The vertex where we are at this iteration
neighbors = component[1] # Vertices that are neighboring (which we haven't visited yet)
# If we are at the closing vertex
if vertex == start:
# Length of this segment
att_vertex_size = G.nodes[vertex].get('size')
# Adding the value of the distance attribute
attrs = {vertex: {'distance' : att_vertex_size}}
nx.set_node_attributes(G, attrs)
else:
pass
vertex_distance = G.nodes[vertex].get('distance')
# For each neighbor, we assign an attribute
for i in neighbors:
# Adding the value of the distance attribute
i_size = G.nodes[i].get('size')
attrs = {i: {'distance' : (vertex_distance + i_size)}}
nx.set_node_attributes(G, attrs) 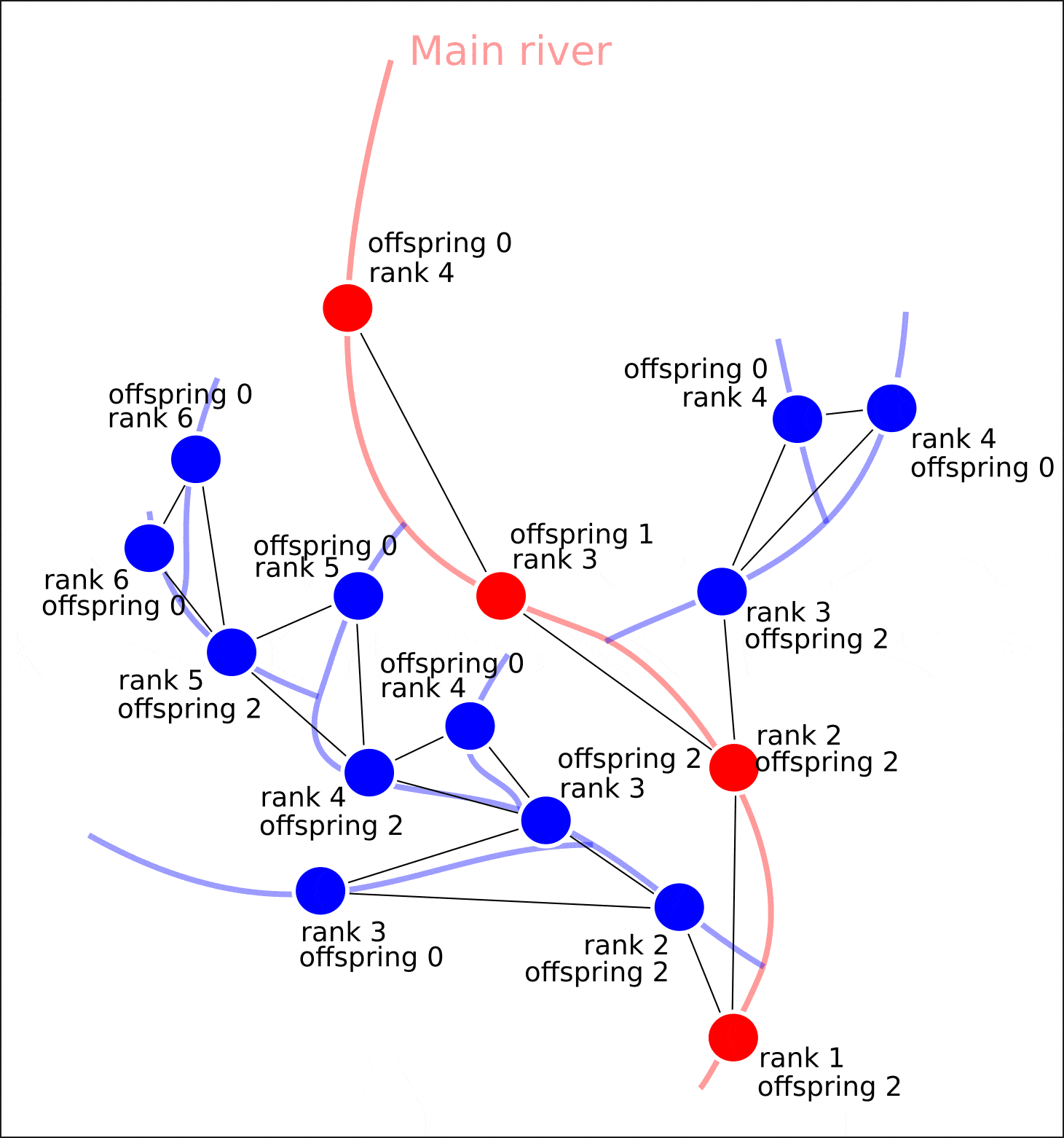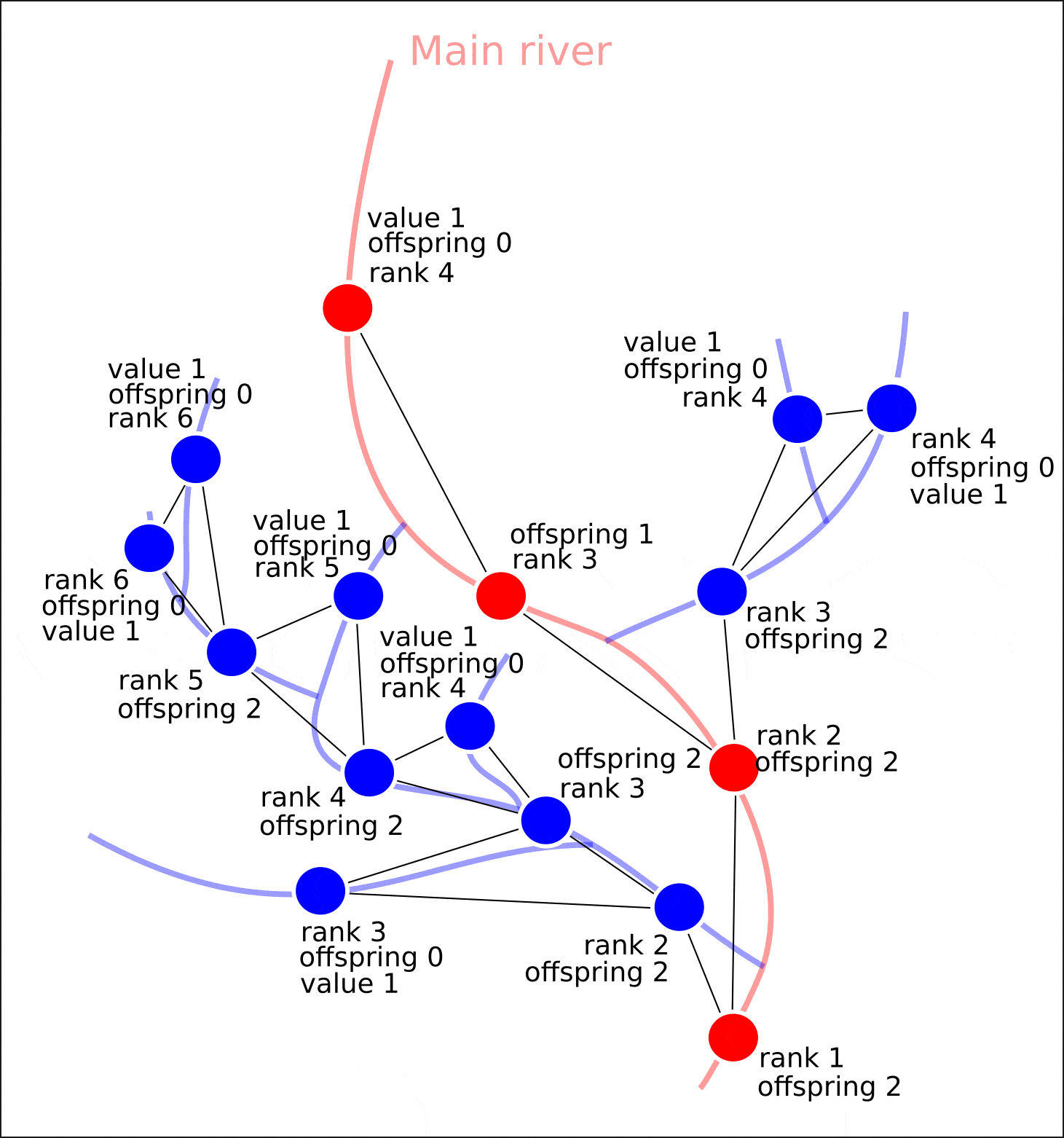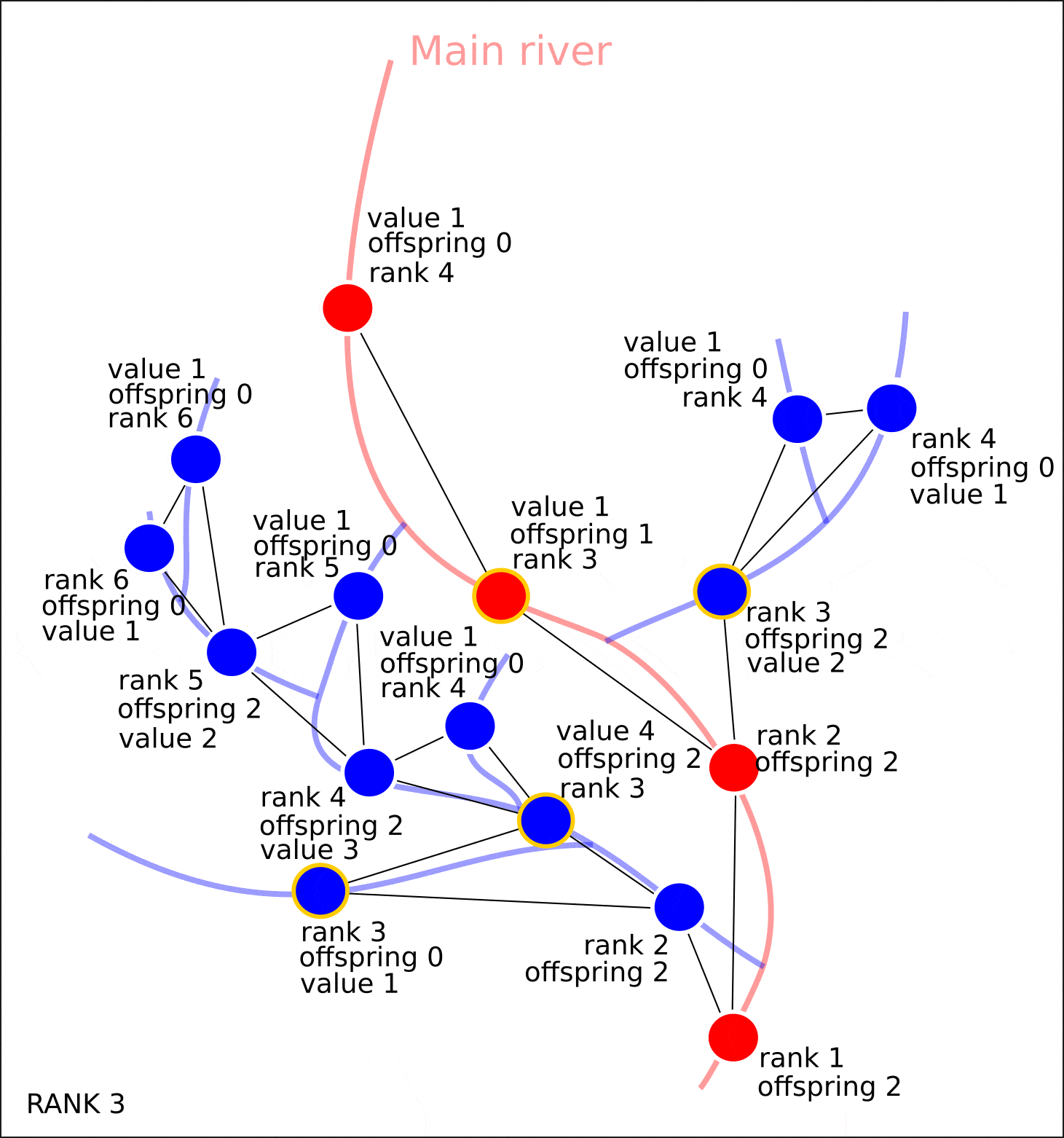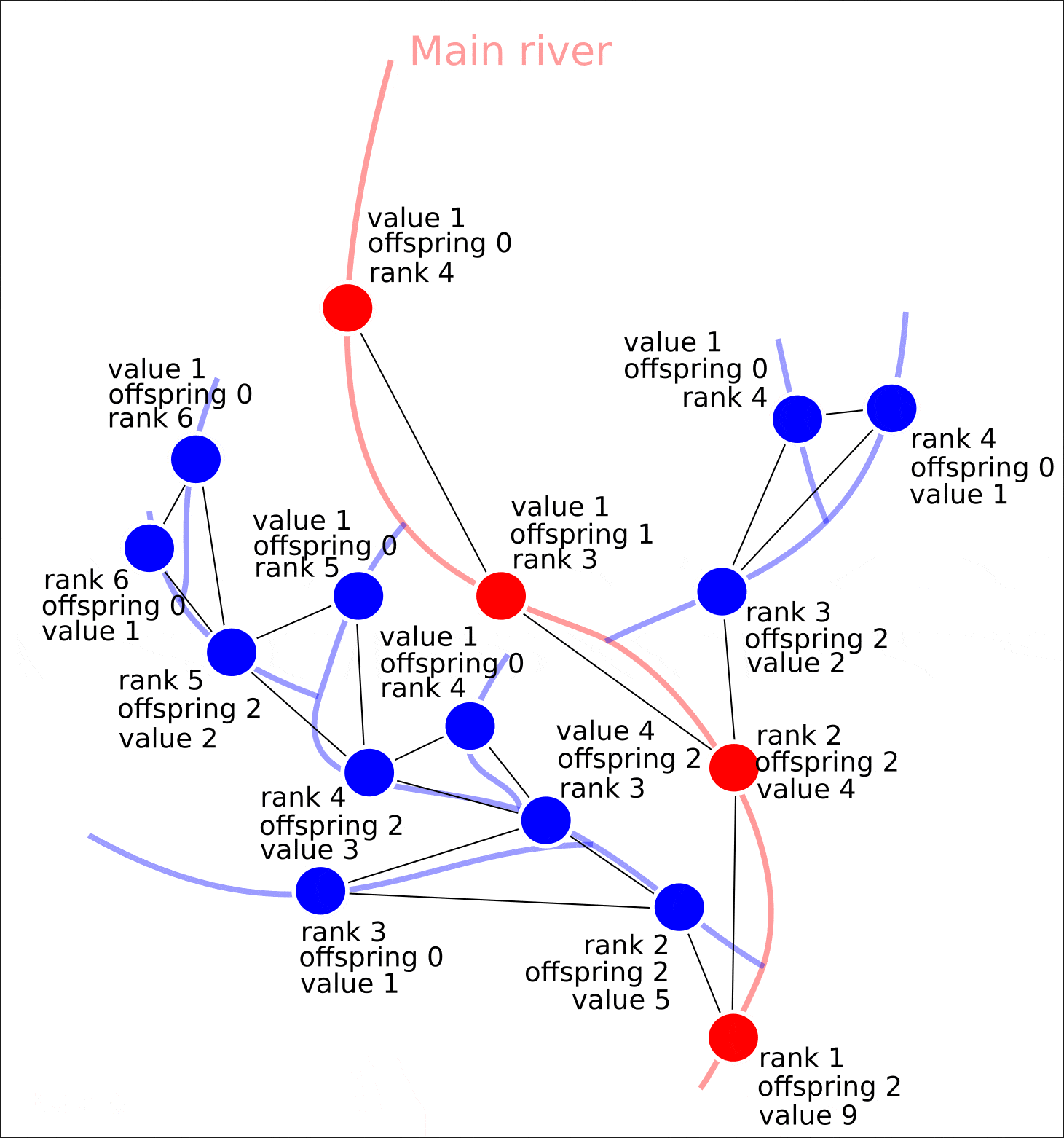
"value", "distance", , , , , , .
8. "rank" "value".

8. ( OpenStreetMap, "rank", - "value")
, . ( ), .
, , .
Python, QGIS . , .
.
Source code repository:
- https://github.com/ChrisLisbon/QGIS_LinesRankingPlugin
Mikhail Sarafanov and Yulia Borisova worked on the algorithm and article .