
Here is a table (20x20) with an integer from 0 to 99 in each of the cells.
The task is to find 4 adjacent numbers without breaking the chain, one after the other, having the largest product. Different variants of 4 adjacent numbers are highlighted in color (two numbers are considered adjacent if they are located no more than 1 cell from each other).
Today we will implement the search algorithm in C #.
First, let's create a 20x20 two-dimensional array and write it to a file:
static void CreateArrayFile()
{
Random random = new Random();
string file = "";
for (int i = 0; i < 20; i++)
{
string line = "";
for (int j = 0; j < 20; j++)
{
line += random.Next(0, 99) + ",";
}
line = line + Environment.NewLine;
file += line;
}
using (FileStream fstream = new FileStream($"array.txt", FileMode.OpenOrCreate))
{
byte[] array = System.Text.Encoding.Default.GetBytes(file);
fstream.Write(array, 0, array.Length);
Console.WriteLine(" ");
}
}

Now we can write the numbers from the file into a two-dimensional array.
string[] lines = arrayFile.Split(Environment.NewLine);
for (int i = 0; i < 20; i++)
{
string[] items = lines[i].Split(',');
for (int j = 0; j < 20; j++)
{
table[i, j] = Convert.ToInt32(items[j]);
}
}
Let's create an Element class to represent the coordinates and value of a number:
public class Element
{
public int Line { get; set; }
public int Column { get; set; }
public int Value { get; set; }
}
According to the conditions of the problem, it is required to find a combination of works. Let's implement the Multiplication class to represent a combination containing an array of numbers and the value of the product of the numbers in the combination.
public class Multiplication
{
public Multiplication()
{
Elements = new Element[4];
}
public Element[] Elements { get; set; }
public int Value
{
get
{
Multiply();
return value;
}
}
int value;
void Multiply()
{
if(Elements[0] != null && Elements[1] != null && Elements[2] != null && Elements[3] != null)
{
value = Elements[0].Value * Elements[1].Value * Elements[2].Value * Elements[3].Value;
}
}
}
The first thing to do is find the nearest neighbors of the number. For example, for the number 40 in our case, the following neighbors:
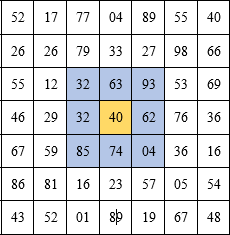
And the number 48 in the lower right corner has only 3 neighbors. It is not difficult to understand that the neighbors of any number are:
table[i-1][j-1]
table[i-1][j]
table[i-1][j+1]
table[i][j-1]
table[i][j+1]
table[i+1][j-1]
table[i+1][j]
table[i+1][j+1]
After making sure that the index is not out of bounds, we get the FindNeighbors method that returns a collection of all the nearest neighbors of a particular number.
According to the problem statement, we need to find a combination of 4 adjacent numbers. To do this, we need a method to find all possible combinations of 4 numbers:
static List<Multiplication> GetFactorCombinations(int line, int column)
{
List<Multiplication> combinations = new List<Multiplication>();
if (table[line, column] != 0)
{
List<Element> firstLevelNeighbors = FindNeighbors(line, column);
foreach (var firstLevelNeighbor in firstLevelNeighbors)
{
Element[] elements = new Element[4];
elements[0] = new Element
{
Line = line,
Column = column,
Value = table[line, column]
};
elements[1] = firstLevelNeighbor;
List<Element> secondLevelNeighbors = FindNeighbors(firstLevelNeighbor.Line, firstLevelNeighbor.Column);
foreach (var secondLevelNeighbor in secondLevelNeighbors)
{
if (!elements[0].Equals(secondLevelNeighbor) && !elements[1].Equals(secondLevelNeighbor))
{
elements[2] = secondLevelNeighbor;
}
if (elements[2] != null)
{
List<Element> thirdLevelNeighbors = FindNeighbors(secondLevelNeighbor.Line, secondLevelNeighbor.Column);
foreach (var thirdLevelNeighbor in thirdLevelNeighbors)
{
if (!elements[0].Equals(thirdLevelNeighbor) && !elements[1].Equals(thirdLevelNeighbor) && !elements[2].Equals(thirdLevelNeighbor))
{
elements[3] = thirdLevelNeighbor;
Multiplication multiplication = new Multiplication
{
Elements = elements
};
if (combinations.Where(p=>p.Elements[0].Value==elements[0].Value&& p.Elements[1].Value == elements[1].Value && p.Elements[2].Value == elements[2].Value && p.Elements[3].Value == elements[3].Value).FirstOrDefault()==null)
{
var nnnn =new Multiplication
{
Elements = new Element[] { elements[0], elements[1], elements[2], elements[3]}
};
combinations.Add(nnnn);
}
}
}
}
}
}
}
return combinations;
}
The method gets the coordinates of a number in the table and checks the value of this number by 0 (When multiplying any number by 0, it always turns out to be 0). Then the method searches for all neighbors of the given number. We iterate over the neighbors of the first level, if the number is not 0, we are looking for all neighbors of the second level ... We
override the Equals method to compare numbers:
public override bool Equals(Object obj)
{
if (this==null || (obj == null) || !this.GetType().Equals(obj.GetType()))
{
return false;
}
else if(Line == ((Element)obj).Line && Column == ((Element)obj).Column)
{
return true;
}
else
{
return false;
}
}
We continue the search to the neighbors of the fourth level, if the numbers are not duplicated, then we add it to our collection.
if (!elements[0].Equals(thirdLevelNeighbor) && !elements[1].Equals(thirdLevelNeighbor) && !elements[2].Equals(thirdLevelNeighbor))
{
elements[3] = thirdLevelNeighbor;
Multiplication multiplication = new Multiplication
{
Elements = elements
};
if (combinations.Where(p=>p.Elements[0].Value==elements[0].Value&& p.Elements[1].Value == elements[1].Value && p.Elements[2].Value == elements[2].Value && p.Elements[3].Value == elements[3].Value).FirstOrDefault()==null)
{
var combination=new Multiplication
{
Elements = new Element[] { elements[0], elements[1], elements[2], elements[3]}
};
combinations.Add(combination);
}
}
The GetFactorCombinations method can be visualized like this:

Now, iterating over our two-dimensional array, we are looking for the largest combination of numbers.
for (int i = 0; i < 20; i++)
{
for (int j = 0; j < 20; j++)
{
List<Multiplication> combinations = GetFactorCombinations(i, j);
foreach (var combination in combinations)
{
if (combination.Value > maxMultiplication.Value)
{
Console.WriteLine(" " + combination.Elements[0].Value + " * " + combination.Elements[1].Value + " * " + combination.Elements[2].Value + " * " + combination.Elements[3].Value + " = " + combination.Value);
maxMultiplication = combination;
}
}
}
}
Console.WriteLine(" = " + maxMultiplication.Elements[0].Value + " * " + maxMultiplication.Elements[1].Value + " * " + maxMultiplication.Elements[2].Value + " * " + maxMultiplication.Elements[3].Value + " = " + maxMultiplication.Value);
If the next combination is greater than maxMultiplication, rewrite it.
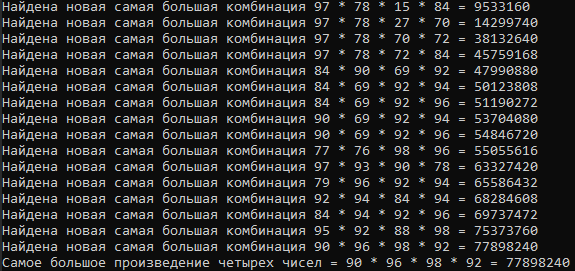
Yes, we did it. We have found the combination of 4 numbers with the largest product.
In fact, we have solved the problem, but the code is hard-coded for specific conditions, a purely procedural method. And if we need to search from a matrix not 20 by 20, but for example 30 by 30 and a combination of not 4, but 5 numbers? each time add another nested loop (to iterate over all with all) ... We
reserve 2 constants for the size of the table, and for the size of the desired combination:
const int TABLE_SIZE = 20;
public const int COMBINATION_SIZE = 4;
Let's rewrite the GetFactorCombinations method to a recursive method:
static List<Multiplication> GetMultiplicationForStep(int line, int column, List<Element> otherElements = null)
{
List<Multiplication> resultMultiplications = new List<Multiplication>();
List<Element> resultElements = new List<Element>();
Element element = new Element
{
Column = column,
Line = line,
Value = table[line, column]
};
if (otherElements == null)
{
otherElements = new List<Element>();
}
if(otherElements!=null)
{
resultElements.AddRange(otherElements);
}
if (table[line, column] != 0)
{
if (otherElements.Where(p => p.Equals(element)).FirstOrDefault() == null)
{
resultElements.Add(element);
}
}
if (resultElements.Count() == COMBINATION_SIZE)
{
Multiplication multiplication = new Multiplication
{
Elements = resultElements.ToArray()
};
resultMultiplications.Add(multiplication);
}
else
{
List<Element> elementNeighbors = FindNeighbors(line, column);
elementNeighbors = elementNeighbors.Where(p => !p.Equals(element)&& otherElements.Where(p=>p.Equals(element)).FirstOrDefault()==null).ToList();
List<Multiplication> newMultiplications = new List<Multiplication>();
foreach(Element neighbor in elementNeighbors)
{
// COMBINATION_SIZE ...
newMultiplications.AddRange(GetMultiplicationForStep(neighbor.Line, neighbor.Column, resultElements).Where(p=>p!=null));
}
foreach(Multiplication multiplication in newMultiplications)
{
if(resultMultiplications.Where(p=>p.Value==multiplication.Value).FirstOrDefault()==null)
{
resultMultiplications.Add(multiplication);
}
}
}
return resultMultiplications;
}
The method works according to the same principle as before, but instead of nested loops, we recursively continue searching for neighbors until the number of found elements is resultElements.Count ()! = COMBINATION_SIZE
After finding the combination, you can display it beautifully in the console:
for (int i = 0; i < TABLE_SIZE; i++)
{
for (int j = 0; j < TABLE_SIZE; j++)
{
if (maxMultiplication.Elements.Where(p => p.Line == i && p.Column == j).FirstOrDefault() != null)
{
Console.BackgroundColor = ConsoleColor.White;
Console.ForegroundColor = ConsoleColor.Black; // ,
Console.Write(table[i, j] + " ");
Console.ResetColor();
}
else
{
Console.Write(table[i, j] + " ");
}
}
Console.WriteLine();
}
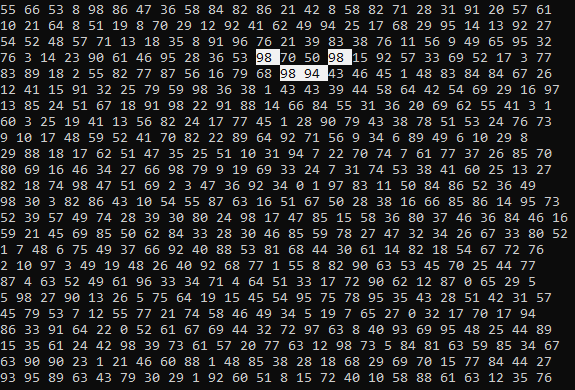
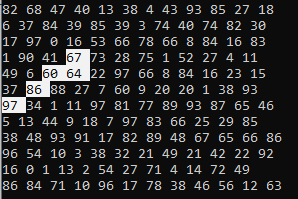
Conclusion
In this article, we got acquainted with one of the options for finding adjacent combinations in the NxN table.
What else can you do:
- You can consider getting rid of multiple iterations of all combinations with all, and other ways to optimize the code.
- Based on the existing algorithm, implement a search for combinations of neighboring numbers on a 3-dimensional array. But this is already another time ...
