Inventing a bicycle or writing a perceptron in C ++. Part 1

Let's write a simple library for implementing a perceptron in C ++

Introduction

Hello everyone, in this post I want to share with you my first experience in writing neural networks. There are a lot of articles on the implementation of neural networks (neural networks in the future) on the Internet, but I don't want to use other people's algorithms without understanding the essence of their work, so I decided to create my own code from scratch.

In this part I will describe the main points of mate. parts that will be useful to us. The whole theory is taken from various sites, mainly from Wikipedia.

Link to the 3rd part with the learning algorithm: habr.com/ru/post/514626

So, let's go.

A bit of theory

Let's agree that I am not claiming the title of "the best machine learning algorithm", I am just showing my implementation and my ideas. Also, I am always open to constructive criticism and advice on the code, this is important, this is what the community exists for.

, .

. .

. :

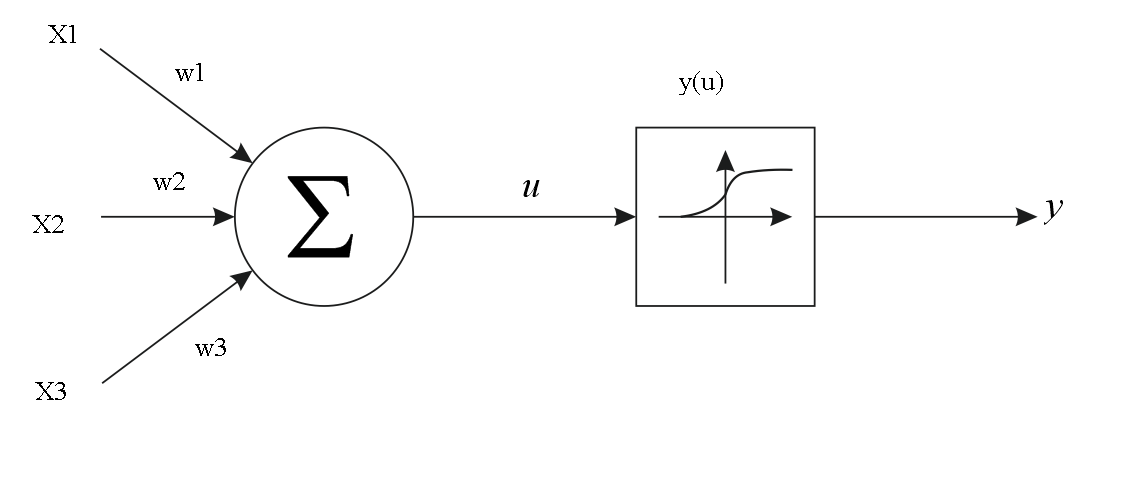
, (1, 2, 3), u (w1, w2, w3), :

u = x1*w1 + x2*w2 + x3*w3

:

. y(u), u – . , .

, , . , , . , – (, ). :

(0; 1), . y(u) .

, . , .

, , .

, . , , ( ).

, 2 : , .

:

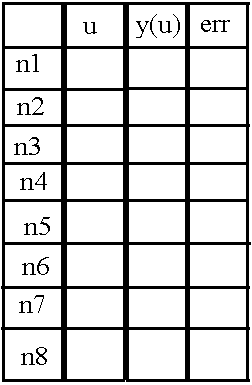
8 ( n1 n8), u, «y(u)» «err», (). «err» .

, , .

, .

. , , , . , .

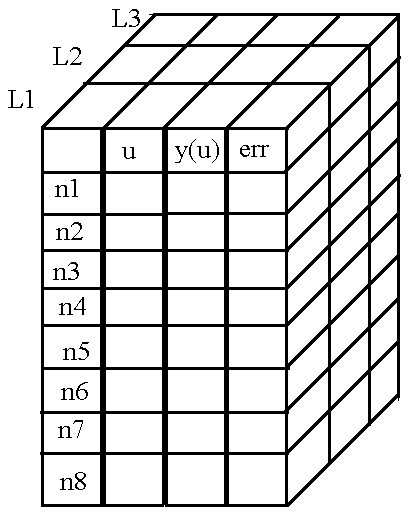
Well, I managed to explain the principles of storing the necessary values in neurons. Now let's figure out how to store the weights of connections between neurons.

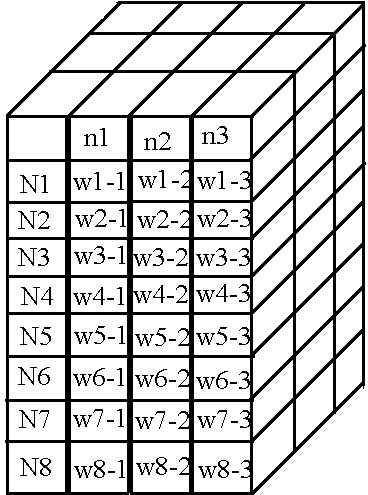
Take the following network for example:

...

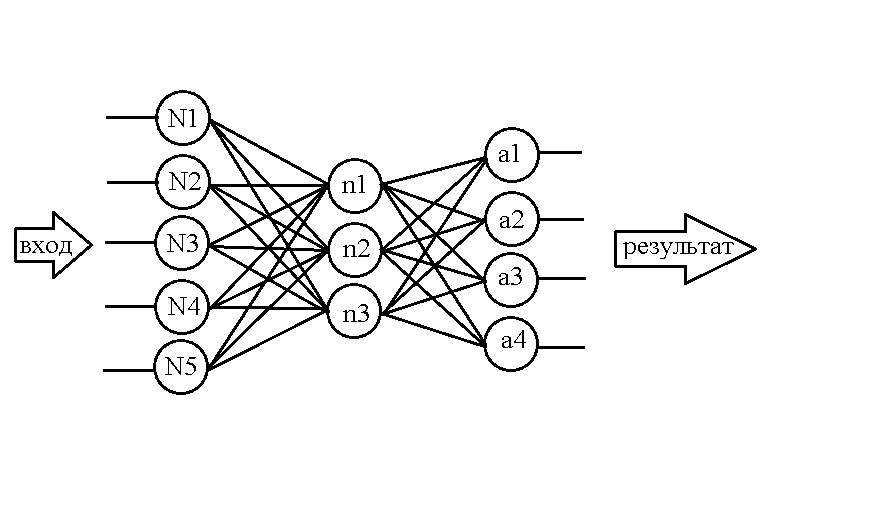
Already knowing how to structure neurons in memory, let's make a similar table for weights:

Its structure is not at all complicated: for example, the value of the weight between neuron N1 and neuron n1 is contained in cell w1-1, similarly with other weights. But again, such a matrix is suitable for storing weights only between the first two layers, but there are still weights in the network between the second and third layers. Let's use the already familiar trick - add a new dimension to the array, but with a caveat: let the line names display the layer of neurons on the left relative to the "bundle" of weights, and the layer of neurons on the right fits into the column names.

Then we get the following table for the second "bundle" of weights:

«», .. , , « » , - , . )).

, .

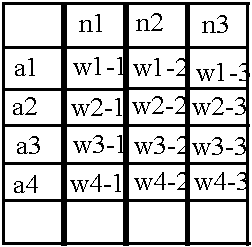
C++. 2

, .

, . .

, !

header —

, . header — ( «neuro.h»). :

class NeuralNet {
public:
    NeuralNet(uint8_t L, uint16_t *n);
    void Do_it(uint16_t size, double *data);
    void getResult(uint16_t size, double* data);
    void learnBackpropagation(double* data, double* ans, double acs, double k);
private:
    vector<vector<vector<double>>> neurons;
    vector<vector<vector<double>>> weights;
    uint8_t numLayers;
    vector<double> neuronsInLayers;
    double Func(double in);
    double Func_p(double in);
    uint32_t MaxEl(uint16_t size, uint16_t *arr);
    void CreateNeurons(uint8_t L, uint16_t *n);
    void CreateWeights(uint8_t L, uint16_t *n);

};

, , header' ). :


//  ,       ,        
#ifndef NEURO_H
#define NEURO_H

#include <vector> //    
#include <math.h> //    ,     
#include <stdint.h> //       ,            .

NeuralNet(uint8_t L, uint16_t *n);

, , - .

void Do_it(uint16_t size, double *data);

)), .

void getResult(uint16_t size, double* data);

void learnBackpropagation(double* data, double* ans, double acs, double k);

, .

, :


    vector<vector<vector<double>>> neurons; //   ,    
    vector<vector<vector<double>>> weights; //   ,       
    uint8_t numLayers; //  
    vector<double> neuronsInLayers; //,      
/*
          ,      ,       ,          ,   
*/
    double Func(double in); //    
    double Func_p(double in); //     
    uint32_t MaxEl(uint16_t size, uint16_t *arr);//       
    void CreateNeurons(uint8_t L, uint16_t *n);//             
    void CreateWeights(uint8_t L, uint16_t *n);

header — :

#endif

header . — source — ).

source —

, .


NeuralNet::NeuralNet(uint8_t L, uint16_t *n) {
	CreateNeurons(L, n); //  
	CreateWeights(L, n); //  
	this->numLayers = L;
	this->neuronsInLayers.resize(L);
	for (uint8_t l = 0; l < L; l++)this->neuronsInLayers[l] = n[l]; //       
}

, :


void NeuralNet::Do_it(uint16_t size, double *data) {
	for (int n = 0; n < size; n++) { //       
		neurons[n][0][0] = data[n]; //       
		neurons[n][1][0] = Func(neurons[n][0][0]); //           
	}
	for (int L = 1; L < numLayers; L++) { //                
		for (int N = 0; N < neuronsInLayers[L]; N++) { 
			double input = 0;
			for (int lastN = 0; lastN < neuronsInLayers[L - 1]; lastN++) {//             
				input += neurons[lastN][1][L - 1] * weights[lastN][N][L - 1];
			}
			neurons[N][0][L] = input;
			neurons[N][1][L] = Func(input);
		}
	}
}

And finally, the last thing I would like to talk about is the function for displaying the result. Well, here we just copy the values from the neurons of the last layer into the array passed to us as a parameter:


void NeuralNet::getResult(uint16_t size, double* data) {
	for (uint16_t r = 0; r < size; r++) {
		data[r] = neurons[r][1][numLayers - 1];
	}
}

Going into the sunset

We will stop at this, the next part will be devoted to one single function that allows you to train the network. Due to the complexity and abundance of mathematics, I decided to take it out in a separate part, where we will also test the work of the entire library as a whole.

Again, I welcome your advice and comments in the comments.

Thank you for your attention to the article, see you soon!

PS: As promised - link to sources: GitHub

Inventing a bicycle or writing a perceptron in C ++. Part 1 and 2