Mathematical foundations of coding and encryption

The information interaction of subscribers in computer and communication networks is subject to disturbances that lead to the occurrence of errors and disturbances of various kinds. In addition to errors in the transmitted messages, unauthorized access to the content of the offender's messages is possible. The fight against these undesirable phenomena has been going on for millennia, but with varying success. The creators of the Internet did not conceive it at all the way it is now. They didn't even think about hackers then.



The main theoretical problems of information confrontation, the tasks of solving them are assigned to the theories of codology, cryptology and steganology, in which the directions of codoanalysis, cryptanalysis and steganalysis are intensively developing all over the world. Practical aspects also do not stand aside, but I will note that in the Russian Federation the activity is not very high, the inertia of young people affects (I myself have already exchanged the 9th decade, but the Habr administration limited the age limit in 1950). My opinion, of course, is limited to observing offspring (up to great-grandchildren) and communication on the Internet, as well as with trainees and employees of the company where I work. The media also add negativity. Some of the youth have grown a little wiser, go over the hill. You can see the behavior of the others yourself.

Guided tour of publications

The development (synthesis) of technical devices requires from the developer certain knowledge, the ability to use them and other skills of this kind. An essential component of such knowledge is mathematics. These are, as a rule, algebra, discrete mathematics, geometry, physics, mathematical logic, etc. Here in the article we will consider algebraic structures not quite in the classical presentation, but with a sufficient level of rigor and accuracy. My main task is to ensure the accessibility and clarity of the presentation of things that I use in my texts and research.



For example, here the GF extension field is used (2 ⁸) and, if we do without it, nothing worthwhile can be stated. My evaluation criteria are simple. Each semester 2, or even 3 exams and tests in different study groups. There I hear and see what I expounded, brought to practice, and what is returned to me in the answers on the examination cards. The analysis of exam answers is very useful, I see that something should have been stated differently, better.



And here the properties Z _Nof a finite numerical residue ring modulo N = pq are used to find a solution to the problem of factorizing large numbers within the framework of a new original approach. It is clear that in each of the subsequent publications it would be unreasonable to transfer part of the standard mathematical tools, therefore, it was decided to collect everything in one place and, if necessary, to address readers here.



Here a group of points of an elliptic curve on a plane is considered and used. The summing operation in a group is of a very special kind, causing perplexing questions, such as how do you manage to add the points of the curve, even from the members of the HEC.

Groups

We first introduce a number of necessary definitions.



Definition . Finite set A -set, collection of any n objects$$${a_1,a_2,..., a_n}$ , listed in any order, but among which there are no duplicates. Sets can be structured, over whose elements one (or more) operation and relations are specified, and unstructured, when no operations are specified.



Below, as a reminder, a table of actions (operations) with finite discrete sets is given, and for clarity, the diagrams also show continuous sets A and B.



Table of operations with sets





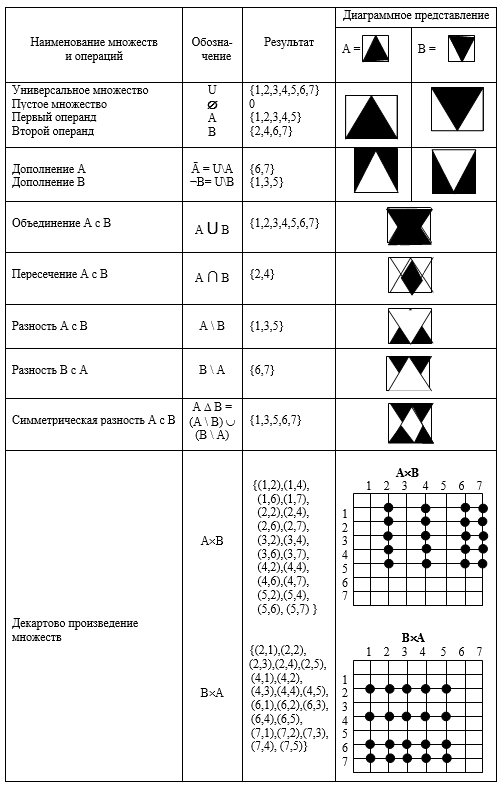
Definition . An operation is a mapping A × A → A or, for example, a · b = c; a, b, c ∊ A. Operations in algebraic structures other than in arithmetic are considered: unary (for example, inversion b ^-1 ), binary, ternary, ..., n-ary (according to the number of places for operands), or multiplication permutations, modular (taking the result by (mod R)), etc. The elements a and b are said to permute or commute if ab = ba.



Definition . A group is a set of G elements (of any nature) over which a single operation is specified, but it can be addition (+) and the group is called additive , its neutral element (0) or multiplication (◦) is called multiplicative, its neutral element (1), but as a rule, these operations are not ordinary arithmetic, but special ones. The group is often denoted by the symbol (G, ◦); among all groups, an important place is given to symmetric groups$$$S_n$ permutations of degree n. Parts of a group's elements that preserve the properties of a group are called subgroups. In essence, these are the same groups, only smaller than the original. This is an informal definition of a group, the formal one will be given a little later.



Group G, which satisfies the commutative law ba = ab for all a, b ε G is called after the mathematician Abel (1802 -1829)Abelian.



An example of an additive group is the set of words of the Hamming code (see here). The operation in this group is 16th order - summing words by (mod2). With this group, the operation of decomposition into contiguous classes of a group of 128 words by a subgroup of the code was performed, and a Keli table was also built, the elements of the group are used in the encoder (basis of the space of dimension 4) and the decoder. In a word, this example clearly demonstrates how even a small group can be used to solve a very important practical problem (communication).



Symmetric permutation (permutation) groups are very important in group theory. This importance is determined by the theorem, which says that for any group arising in an arbitrary subject area, there is a symmetric group (subgroup) isomorphic to it on permutations. Then the task of studying it is simplified for the researcher of a new open group. Almost all the properties of the isomorphic permutation group are valid in the new group.



Let's start with a simple example. N elements are given (we denote them by the numbers 1,2,3, ..., n) and we form permutations from them, the number of which is n! = 1 2 3 ... n. Let's restrict ourselves to the value n = 3, then 3! = 6.



Definition . Group order - The number of elements in a group is called its order. In the example, the number 6 is the order of the group.



In a group, each element also has an order that is a divisor of the group order.

Definition . The order of an element of a group is the smallest exponent of an element in a multiplicative group (multiplicity in the additive b + b + b + b + ... b = nb = 0, order = n) at which it becomes a neutral element, for example ($$$_4$ )³= 1, order ord ($$$_4$ ) = 3.



In the symmetric group$$$S_n$ operation is the multiplication of permutations. This multiplication is similar to matrix multiplication, since each permutation of degree n is associated with an n × n square permutation matrix in which each row and column contains a single unit. This is shown below for the symmetric group$$$S_3$ .







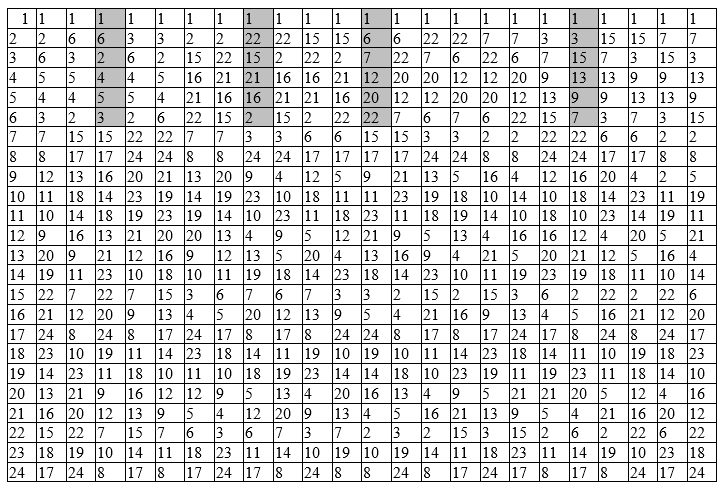
For the convenience of working with a group and its elements, mathematician Keli proposed a table of group operations (of limited size). In the cell at the intersection of a row and a column, the result of the operation with the elements that denote them is put. The result (as well as the designation of rows / columns) in the table is represented by decimal element numbers, which saves space.



Multiplication table of elements (permutations) of a group $$$S_3$





Filling in 36 cells of the multiplication table is simplified by using the properties of the Keli table.

- All rows and columns contain elements of the entire group.

- The extreme columns are lexicographically ordered and oppositely directed (1st top / bottom - the last one is vice versa)

- On the main diagonal of the table there are squares of elements, if there is 1, then the element corresponding to it is involution; involutions in$$$S_3$ are$$$_1,_2,_3,_6$

- The symmetry of the positions of the elements is fulfilled with respect to the diagonals of the matrix.

The properties of the table allow, when filling it, to restrict the calculations to only 13 pairs of elements (they are shown above).

Symmetric group $$$S_4$

Group $$$S_3$ has a small order (6) and is not very convenient for illustrating properties. Below we will give examples with the symmetric group$$$S_4$ 24 orders. All even permutations of degree n form analternatingsubgroup in the symmetric group, denoted by the symbol A_n.







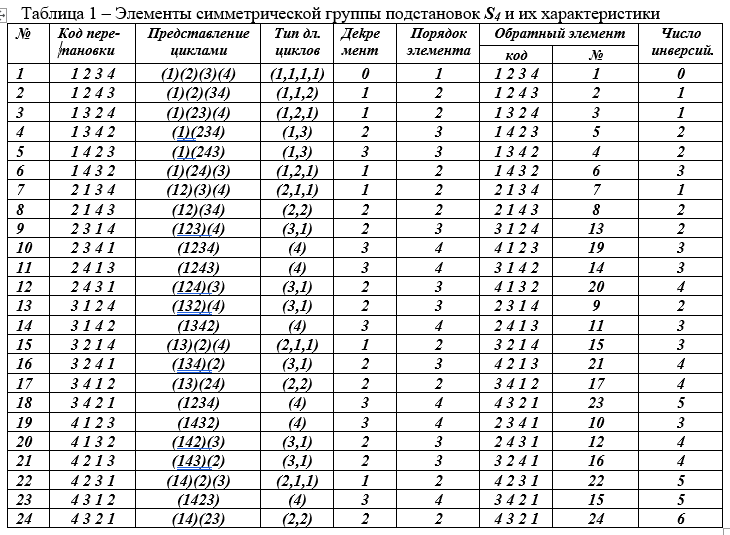
Table 2 can be used to find the products of any pair of elements$$$S_4$ or for their whole chain, but are found by sequential multiplication of the result by the next element. You cannot rearrange the elements in the work. Permutation multiplication is not commutative, as is matrix multiplication. One element, when multiplied by itself many times until you get 1, forms a cyclic group of all intermediate results. The order of such a cyclic subgroup is the order of the generator; it must divide the order of the original large group.



According to the multiplication table, there are subgroups within a large group. Remember that the order of the smaller subgroup must divide the order of the larger.

We construct a cyclic group withelementp₁₄generating. We enter table 2. In line 14 we find at the intersection with p₁₄column element p ₂₄ ; in line 24 we find the element p ₁₁ in the cell of intersection with column 14, and finally in the cell of row 11 at the intersection with column 14 we find the element p ₁ , i.e. neutral element 1. So, p ₁₄ · p ₁₄ · p ₁₄ · p ₁₄ = p ₁ , these are elements of the 4th order subgroup, the value of which completely divides the order 24: 4 = 6. For it, you can construct the Keli table and it does not contain will appear no elements other than those found. In this subgroup, the elements p ₁₄ and p ₁₁ have the 4th order, and p _{24 the} second is an involution.

Group morphisms

A mapping f of a group (G, *) to a group (G ', ◦) is called a homomorphic (or homomorphism) if, for any a, b ∊ G, f (a * b) = f (a) ◦f (b). Usually these equalities continue as f (e) = e ',

f (a ^-1 ) = (f (a)) ^-1 . The notation to the right of the equality denotes the image and is called the image; to the left, the preimage of the mapping f. In the general case, operations on the image and preimage do not coincide. The inverse image of the identity (G ', ◦) under the homomorphism f is called the kernel of this homomorphism and is denoted by ker f. A well-known example from school years is such a mapping

log (a◦b) = log (a) + log (b).



Elements of the image with an operation on them (+), and in the preimage the elements are connected by the operation (◦) of multiplication. A homomorphic image of a group is a group (subgroup), that is, if an f-homomorphism of G onto G 'and G is a group, then G' is also a group. A homomorphism is a generalization of group isomorphism: if f is a one-to-one homomorphic mapping of G onto G ', then it is isomorphic, which is denoted as G≈G'.

Two groups G and G 'with operations (·) and (*) are called isomorphic if there exists a mapping f: G → G' such that (the mapping f preserves the group operation) of the image;



Theorem. Let H be a normal subgroup of a group G and G = G / H. Then the mapping f of the group G onto G given by the formula f (a) = ais a homomorphism. The kernel of this homomorphism is H. This homomorphism is often called natural (canonical).

Group homomorphisms are essentially exhausted by canonical homomorphisms.



Let us decompose the group G of order 24 with respect to its subgroup H = {1,8, 17,24} into cosets and construct for this decomposition a quotient group with respect to the subgroup H. For this purpose, we write in columns the left and right products of elements of the subgroup H.







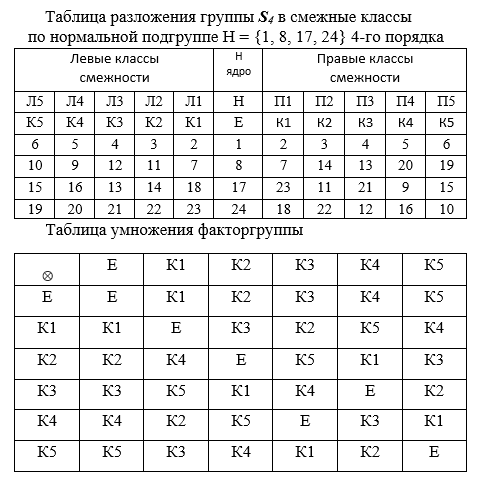
In the table of decomposition of a group G of order 24 into cosets with respect to the subgroup H, columns l1, l2, l3, l4, l5 are designated the names of the left and n1, n2, n3, n4, n5 - right cosets, the leading representatives of the classes, one per column, are written in next line.



The middle column H is a fourth-order group (the kernel of the homomorphism). The columns are filled with the products of the leading representatives of the classes and the elements of the group H. After the columns are filled in, the classes are compared. If the compositions of the left and right classes coincide, then they simply speak of coset classes and denote H = K0, K1, K2, K3, K4, K5. Moreover, the subgroup H is called normal . When filling out the table, the leading representative of the next class selects the smallest element G from those not included in the already built classes.



The obtained cosets are further considered as elements of a new group called the quotient group of the group G by the subgroup H (the quotient group G = G / H is denoted ). The operation in this new group is the multiplication of classes: for each pair of classes, for example, K3 × K5 = K2, a 4 × 4 table is constructed, in which the rows are marked with the elements of the first factor, and the columns - the second. Further, multiplication is performed as in the group G. The result of such multiplication gives 16 elements, but they all belong to the same class, in our case the class K2.



In addition to isomorphism mappings, homomorphisms are endomorphisms and automorphisms. A homomorphism of a group G into itself is called an endomorphism, and an isomorphism of a group G onto itself is an automorphism. These concepts are comparable to the concepts of maps of unstructured sets by injection, surjection and bijection.



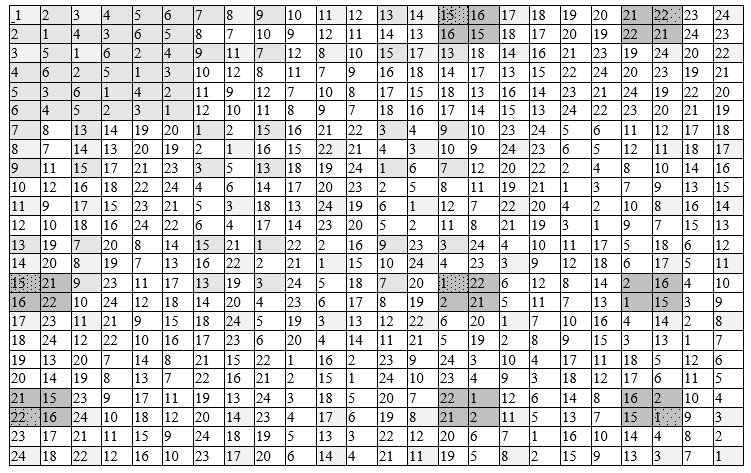
Table 2 - Keli symmetric group$\$\; inline\; \$\; S\_4\; (multiplication\; P\_k\; =\; P\_i\; P\_j)$$ inline $

Commutator

To each pair of elements a, b ∊ G we associate an element called the commutator of this pair

[a, b] = a ^-1 b ^-1 ab. The subgroup K of a group G generated by all its commutators is called the commutator subgroup of the group G or a derived subgroup.







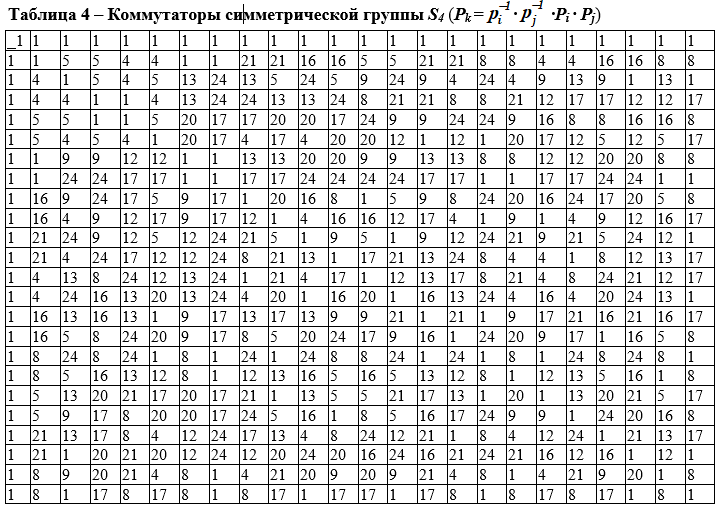
A group G is called solvable if the chain G ⊇ G '⊇ G' '⊇… ⊇ G ⁽ⁱ⁾ ⊇ ..., where each subgroup G ⁽ⁱ⁾ is the commutator subgroup of the previous one, terminates after a finite number of steps on the unit subgroup, for example, G ^(f) = 1.

In Table 4, the alternating subgroup G '= A _{4 of} order 12 is normal, from G =$$$S_4$ order 24, since the left and right cosets for this subgroup coincide (the classes are the same complement to the full group$$$S_4$ ). Table 4 is then collapsed into a smaller 4 × 4 table (commutator) containing elements G '' = {1,8,17,24} of a new subgroup whose commutator is 1. Table 4 illustrates the solvability of the group$$$S_4$ .

Conclusion

The article discusses some of the main provisions of group theory, which are often used in publications of a technical (not theoretical and mathematical) nature. The understanding of the text of such publications is largely determined by the possession of mathematical tools.



For a group, an example and a technique of its homomorphic mapping into a quotient group are given.

Numerical examples are designed to serve to ensure the accessibility of the material presented and to a large extent help its understanding and assimilation, with careful analysis or even repetition with a pencil in hand. Which is simply missing in the classic manuals. This is often attributed to saving space and time.

I am awaiting a reaction from readers, which will make it clear whether to continue in this style or not.

Literature

Avdoshin S.M., Nabebin A.A. Discrete Math. Modular algebra, cryptography, coding. - M .: DMK Press, 2017.-352 p.

Akimov O.E. Discrete mathematics. Logic, groups, graphs - Moscow: Lab. Base. Zn., 2001.-352 p.

Anderson D.A. Discrete mathematics and combinatorics), Moscow: Williams, 2003, 960 p.

Berlekamp E. Algebraic coding theory. -M .: Mir, 1971.- 478 p.

Vaulin A.E. Discrete mathematics in computer security problems. H 1- SPb .: VKA im. A.F. Mozhaisky, 2015.219 p.

Vaulin A.E. Discrete mathematics in computer security problems. H 2- SPb .: VKA im. A.F. Mozhaisky, 2017.-151 p.

D. Gorenstein, Finite Simple Groups. Introduction to their classification.-M .: Mir, 1985.- 352 p.

Graham R., Knut D., Ptashnik O. Concrete Mathematics. Foundations of Informatics.-M .: Mir, 1998.-703 p.

Elizarov V.P. End rings. - M .: Helios ARV, 2006. - 304 p.

Ivanov B.N. Discrete mathematics: algorithms and programs - M .: Lab. Base. Knowledge., 2001.280 p.

Yerusalimsky Y. M. Discrete mathematics: theory, problems, applications - M .: Vuzovskaya kniga, 2000.280 p.

Lidl R., Niederreiter G. Finite fields: In 2 volumes.Vol. 1 -M .: Mir, 1988. - 430 p.

Lidl R., Niederreiter G. Finite fields: In 2 volumes.Vol. 2 -M .: Mir, 1988. - 392 p.

Lyapin E.S., Aizenshtat A.Ya., Lesokhin M.M., Exercises on the theory of groups.- Moscow: Nauka, 1967.-264 p.

Mutter V.M. Fundamentals of anti-jamming information transmission. -L. Energoatomizdat, 1990, 288 p.

A.A. Nabebin, Discrete Mathematics, Moscow: Lab. Knowledge., 2001.280 p.

F.A. Novikov Discrete mathematics for programmers.- SPb .: Peter, 2000.-304 p.

Hall M. Group Theory.-M .: Izd. IL, 1962.- 468 p.

Shikhanovich Yu.A. Groups, rings, lattices. - SPb .: Kirtsideli, 2006. - 368 p.

Shneperman L.B. A course of algebra and number theory in problems and exercises: In 2 hours Part 2.-Mn .: Vysh. shk., 1987.-256 p.

Shneperman L.B. Collection of problems in algebra and number theory. - Minsk: Design PRO, 2000. -240 p.