Crazy unconditional exchange

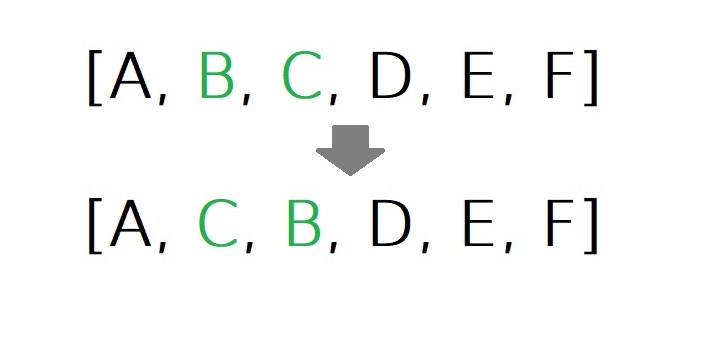
Recently I came across a task in an immutable way to swap two elements in an array by their indices. The task is pretty simple. Therefore, solving it in a reasonable way:

const swap = (arr, ind1, ind2) =>
  arr.map((e, i) => {
    if (i === ind1) return arr[ind2]
    if (i === ind2) return arr[ind1]
    return e
  })

I wanted to solve it in a crazy way. I thought it would be interesting to solve this problem:

• Without comparison operators and logical operators ( &&, ||, ...)
• Without loops and ifs and ternary operators
• Without using additional data structures
• No casting

Reducing the problem to a smaller one

Indeed, this task can be reduced to a smaller one. In order to demonstrate this, let's rewrite the code from above in this way:

const swap = (arr, ind1, ind2) => {
  return arr.map((elem, i) => {
    const index = i === ind1 ? ind2 : i === ind2 ? ind1 : i

    return arr[index]
  })
}

index, . — ind1, ind2. ind2 ind1. , — — index .

index getSwapIndex(i, ind1, ind2).

const getSwapIndex(i, ind1, ind2) {
  return i === ind1
     ? ind2
     : i === ind2
       ? ind1
       : i
}

const swap = (arr, ind1, ind2) => arr.map((_, i) => arr[getSwapIndex(i, ind1, ind2)])

swap . ,

— . getSwapIndex , . , 1 0. 1 , 0 .

:

type NumberBoolean = 1 | 0

""

const or = (condition1, condition2) => condition1 + condition2 - condition1 * condition2

, 1 0. "" .

or(0, 0) => 0 + 0 - 0 * 0 => 0
or(0, 1) => 0 + 1 - 0 * 1 => 1
or(1, 0) => 1 + 0 - 1 * 0 => 1
or(1, 1) => 1 + 1 - 1 * 1 => 1

, :

const or = (c1, c2) => Math.sign(c1 + c2)

Math.sign(-23) = -1
Math.sign(0) = 0
Math.sign(42) = 1

, , .

const R =  ? R1 : R2
//   -   , R1, R2 -  .
// ,
const R = P * R1 + (1 - P) * R2
//   -       .     === true,  P    1,    === false,  P    0.

P === 0, R = 0 * R1 + (1 - 0) * R2 = R2.

P === 1, R = 1 * R1 + (1 - 1) * R2 = R1.

— .

ternary(c, r1, r2) :

function ternary(p: NumberBoolean, r1: number, r2: number): number {
  return p * r1 + (1 - p) * r2
}

. :

isEqual(a: number, b: number): NumberBoolean

:

const isEqual = (a, b) => {
  return 1 - Math.sign(Math.abs(a - b))
}

Math.abs(-23) = 23
Math.abs(0) = 0
Math.abs(42) = 42

, , . a b — , :

isEqual(a, b)
 => 1 - Math.sign(Math.abs(a - b))
 => 1 - Math.sign(Math.abs(0))
 => 1 - Math.sign(0)
 => 1 - 0
 => 1

, :

isEqual(a, b)
 => 1 - Math.sign(Math.abs(a - b))
 => 1 - Math.sign(Math.abs( ))
 => 1 - Math.sign( ))
 => 1 - 1
 => 0

.

--

getSwapIndex :

const getSwapIndex = (i, ind1, ind2) =>
  ternary(isEqual(i, ind1), ind2, ternary(isEqual(i, ind2), ind1, i))

:

const isEqual = (a, b) => 1 - Math.sign(Math.abs(a - b))

const ternary = (p, r1, r2) => p * r1 + (1 - p) * r2

const getSwapIndex = (i, ind1, ind2) =>
  ternary(isEqual(i, ind1), ind2, ternary(isEqual(i, ind2), ind1, i))

const swap = (arr, ind1, ind2) => arr.map((_, i) => arr[getSwapIndex(i, ind1, ind2)])

, , .

, , :

const getSwapIndex = (i, ind1, ind2) => {
  const shouldSwap = or(isEqual(i, ind1), isEqual(i, ind2))

  return ternary(shouldSwap, ind1 + ind2 - i, i)
}

:

, !