
Introduction
To type on the keyboard, sit or stand still. Gamepads, by contrast, are portable and compact. By controlling them, you can walk around the room or lie down on the sofa.
Due to the small number of buttons on the gamepad, no one considered them as a means of entering voluminous texts, for example, in programming.
However, analog sticks (and most gamepads have two) have the potential to provide endless input options. The question comes down to choosing the right gestures for maximum efficiency and minimum tension on the thumbs.
There are many ways to enter text for gamepads. If you've ever played console games, chances are you've used one of them.

On- screen text entry in Legend of Zelda In Legend of Zelda, the player must take turns selecting letters using the D-pad with arrows and each time pressing the confirm button to add a letter to the text input field.
Since then, more efficient input methods have been developed. If you are interested, then read the article on Gamasutra .
Unfortunately, all the input methods I've found have two major flaws that make them unsuitable for serious work:
- They're not fast enough
- They require visual feedback
The need for speed is clear. Visual feedback is unacceptable because it takes up valuable screen space and distracts the user, which can interfere with flow and slow things down.
However, in the absence of feedback, all gestures must be memorized and practiced until you can enter them with sufficient accuracy. Video games are unlikely to force the user to spend a couple of weeks learning how to enter text, but for a way to enter text that can be used in any program, the price is acceptable, and the training itself is like mastering touch input.
In this post I will briefly talk about the steps involved in creating a text input system for gamepads that is suitable as a replacement for volumetric keyboard input.
Deciding on gestures
To begin with, I created a tool for visualizing the movement of analog gamepad sticks based on
pygamethe Python language. For clarity, I supplemented the tool so that it not only shows the current positions of the sticks, but also the previous positions of increasingly lighter shades of gray, so that you can see the paths along which the sticks move.
The figure below shows the simultaneous movement of both analog sticks inward, upward, outward, downward, inward again, and back to center.
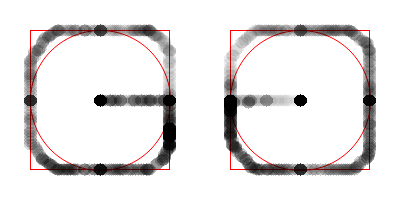
Visualizing patterns of movement of analog sticks
The first thing I noticed is that since the neutral state of the controller is the sticks in the center, all input options must be reachable from this neutral state and they must all end with the return of the sticks to the center.
With these limitations in mind, I figured out that the simplest possible input would be to move one of the sticks in any direction and back to center.
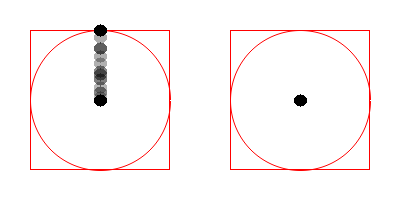
The left stick has moved up and back to the center.
How many directions and which directions can be precisely selected blindly? Consider the following example.
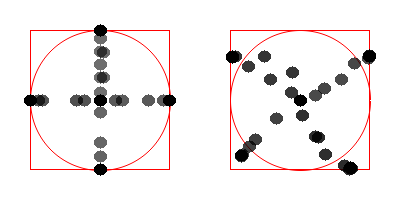
The left stick moved up, down, center, left and right, and the right stick moved diagonally
A few minutes of experimentation showed that it was possible to accurately select directions along the axes, and input in other directions was much less accurate (as seen in the previous image).
The next simplest input methods found were one-stage and two-stage circular motions.
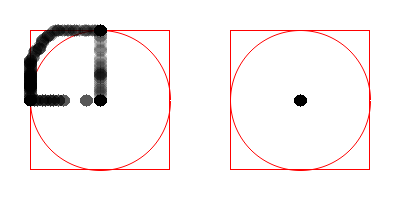
Left stick moved up, left and back to center
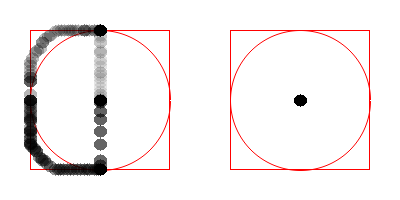
The left stick moved up, left, down and back to the center.
Taking into account all the gestures invented so far, we got 4 + 8 + 8 = 20 input options on each stick.
Of course, both sticks can be moved at the same time, creating combined input gestures.

Both sticks move up and back to the center at the same time.
When you combine gestures, a total of 20 * 20 + 20 + 20 = 440 input options is obtained, which, in my opinion, is more than enough.
Encoding gestures
I divided the input space of each stick into 4 sectors and assigned a number to each sector.
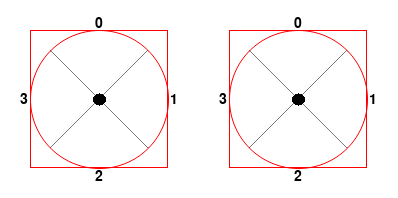
Input spaces divided into sectors
Then I set a threshold area around the center to help determine if the stick is in the neutral position or in one of the sectors.

Circular sill around the center
As you can see, the radius of the sill is quite large. Through experimentation, I have determined that this is the best radius that provides the least amount of error.
When any of the sticks are off-center, crossing the threshold area, the input sequence begins. When both sticks return to the center inside the threshold area, the sequence is considered complete and is converted into a pair of tuples describing the movement of the sticks.
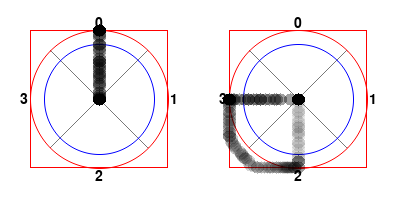
Move sticks for input ((0,), (2, 3))
Linking gestures to actions
In this case, the actions are just keyboard keys. Gamepad trigger buttons can be bind to the Shift, Ctrl, Alt and Super keys, which is convenient because these keys are used in combinations (for example, Ctrl-C).
To determine the optimal binding of the entered gesture and key, I used a keylogger to record all keystrokes and analyzed the frequency of each key for several weeks.
The most frequently pressed keys should be tied to the simplest (and therefore the fastest) gestures. I estimated the complexity of the gesture by adding the lengths of the inputs of each stick. For example, the input shown above ((0,), (2, 3)) has complexity 1 + 2 = 3.
In this case, when entering from one stick, alternating use of two sticks will be faster than multiple inputs from the same stick, so it is often better to bind the keys to be typed to different sticks.
Following this logic, I first generated all possible input options from one stick and grouped them by difficulty. I counted the number of inputs in each difficulty group and took the number of keys from a sorted list of the most frequent keys.
My goal was to split these keys into two groups, one for left stick input and one for right stick. To find ideal groups, I created a graph in which the nodes were the keys, and the weighted edges were the frequencies of the key combinations.
I cyclically removed the lowest weight edge until the graph became bipartite. If the graph became disconnected, I recursively applied the partitioning algorithm to the connected components, and at the end combined the groups into independent sets.
Consider the following example. The first group of complexity consists of all inputs with a complexity of 1, that is
((0,), ()), ((1,), ()), ((2,), ()), ((3,), ()), ((), (0,)), ((), (1,)), ((), (2,)), ((), (3,)).
There are 8 inputs in this group, so we take the 8 most frequent keys from the sorted list. This is
'e', 'o', 't', 'a', 'i', 's', 'j', 'r'. Create a graph with these keys as nodes and assign weights to the edges between these nodes corresponding to the frequency of each key combination.

The e and r keys are most often combined, so they must be attached to different sticks.
When removing weak edges from the graph, it sooner or later turned into unlinked.
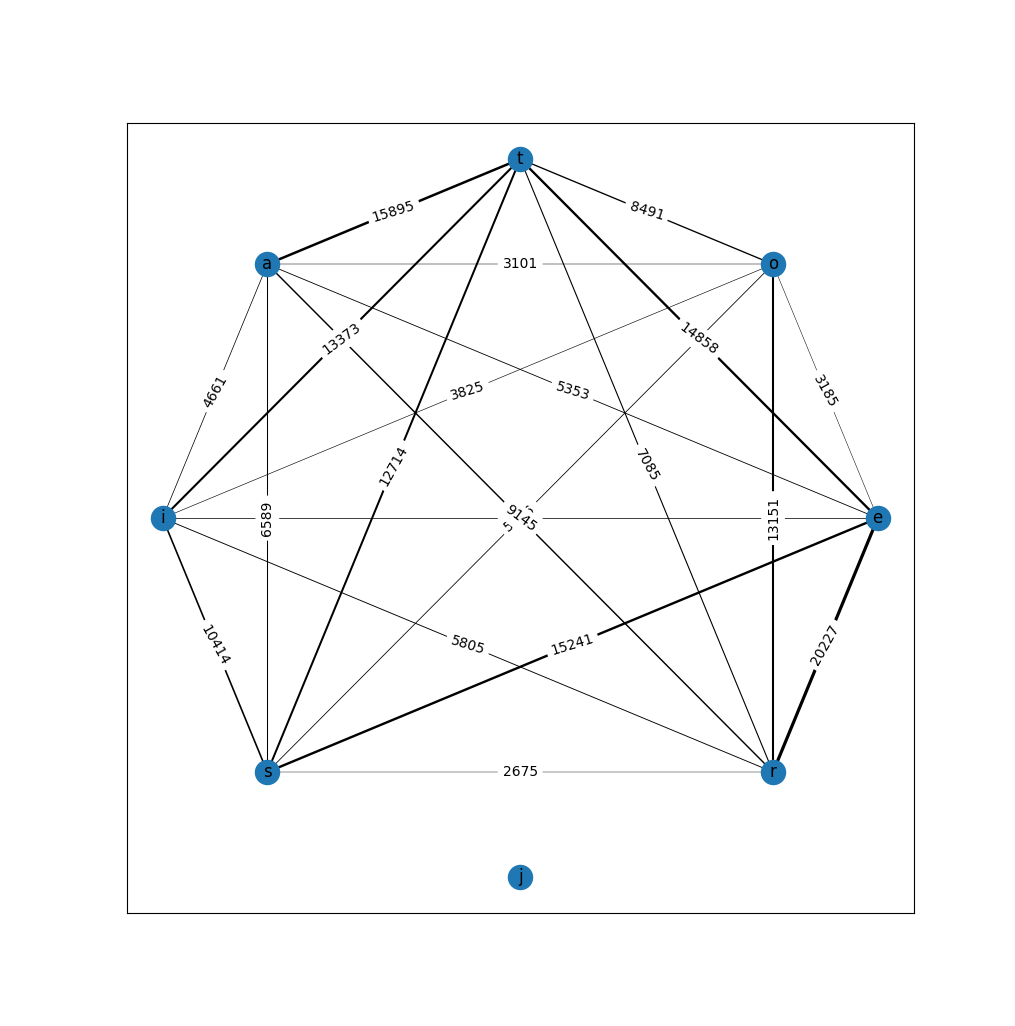
The j key is common, but is isolated.
You may be wondering why the key
jis one of the 8 most frequent keys, but has such weak links to the rest of the frequent keys. The reason is that it is jactively used when working with VIM plus, on my system this is part of a hotkey combination for switching between windows. Therefore, it is more often used in isolation than in the text.
Since the graph is disconnected, I continue to apply the algorithm to connected components. A subgraph consisting only of a node
jis already bipartite ( j+ empty set). I am recursively applying the algorithm to another component.
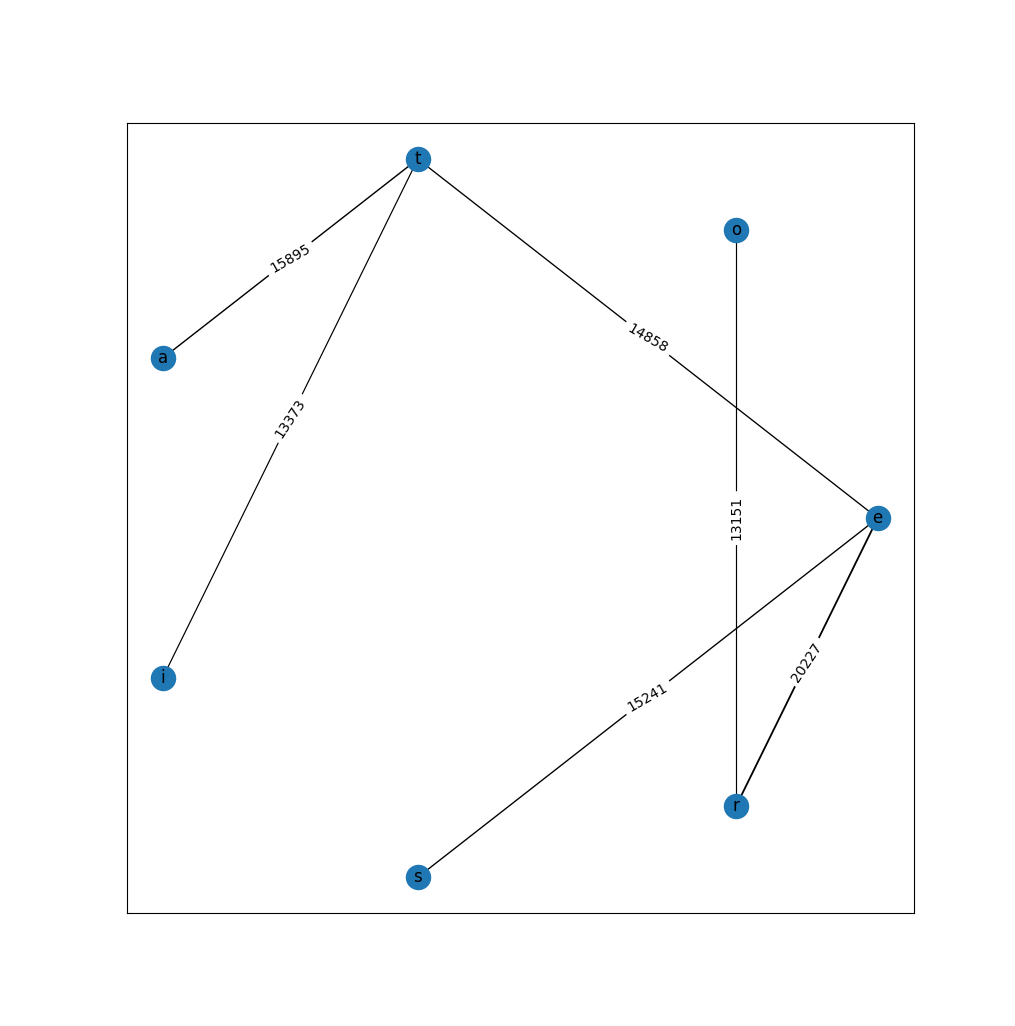
After removing the weakest edges, the component becomes bipartite.
The component can then be easily split into two groups without edges between the nodes in the group.
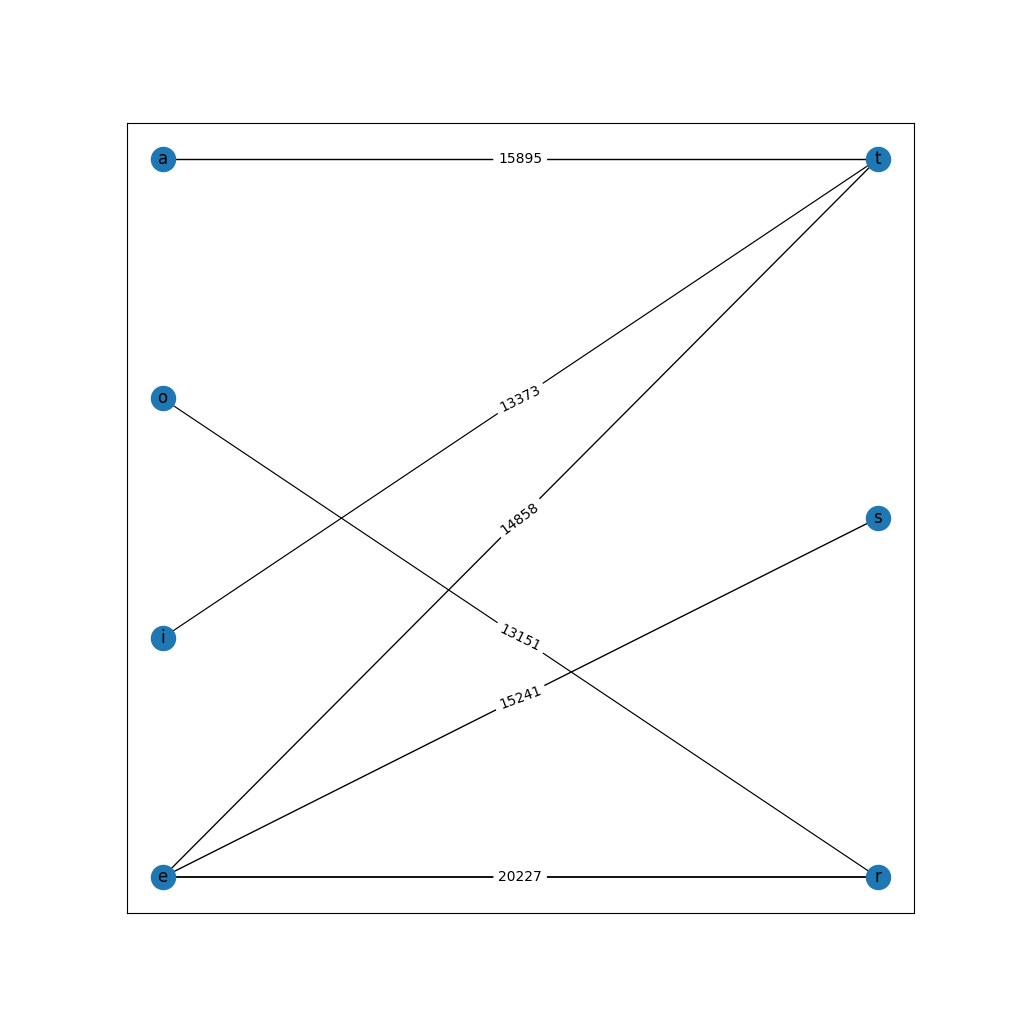
Bipartite Component Scheme
In the end, I combine the bipartite sets.
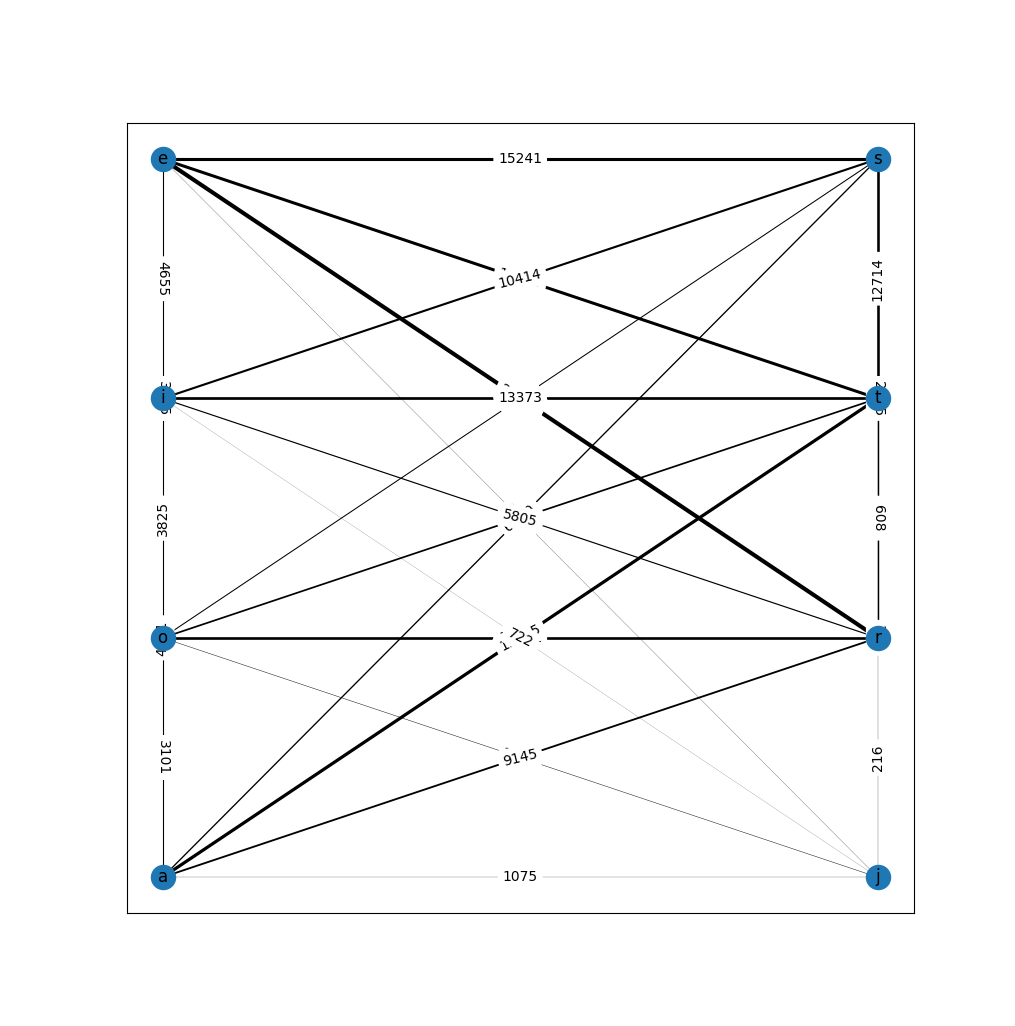
The grouping obtained for the first 8 keys
As you can see, the strongest links (the most frequent keyboard shortcuts) are located between the nodes on different sides, which is exactly what I wanted.
I repeated this process for the other difficulty groups (single stick inputs only). Then I generated all possible combined inputs, grouped them again by difficulty, and assigned the remaining keys to those input options. Since combined inputs require the use of both sticks, the problem of dividing the keys into two groups does not arise here.
I used the
pyautoguiPython package to generate keyboard events when actions are triggered.
Practice
I used the same touch trainer that I
ktouchalready used to teach typing almost two decades ago. For this purpose, I have created specialized lessons.
Practicing analog input on a gamepad in ktouch
Observations
- Although the Python process running this input system usually consumed no more than 10% of the CPU resources, if it had to be constantly running in the background, then I would reimplement it and optimize it in a lower-level language so that the processor can do more costly tasks.
- After buying a DualShock4 gamepad, I realized that I can do diagonal input quite accurately. The integration of diagonal input will reduce the number of more complex input options, and therefore increase the speed.
- , . , . , , , .
- , . , , .
- . .
In just a couple of days, I created an efficient input system for gamepads. There are many enhancements that can be made, but this check of concept demonstrates that efficient gamepad typing is possible. The project code is posted on github .