
Quantum technology helps us in a wide variety of areas. For example, when we need to measure a very weak signal, and quantum noise in the system gets in the way. This is a traditional problem, for example, in gravitational wave detectors, in which quantum fluctuations in the amplitude and phase of the laser used to measure the position of the mirrors interfere with the observation of gravitational waves. I talked about this in my article about the Einstein Telescope detector , which will appear in Europe in the near future.
In our experiment, we got a small prototype of this detector.
A preprint of our article about this experiment was released today: Squeezed-light interferometry on a cryogenically-cooled micro-mechanical membrane .
1. Brief introduction
There are many weak forces in nature that scientists would love to study.
The problem is that we cannot directly measure the force, but can only observe its effect on different bodies.
The easiest and most effective way to measure force is to use a pendulum. The force moves the pendulum, and we measure that displacement. When the frequency of the force is close to the resonant frequency of the pendulum, the displacement is greatly enhanced and we can observe a good signal.
It is convenient to use light to measure the displacement of the pendulum. When we shine a laser on a pendulum covered with a reflective substance, the phase of the reflected light contains information about the displacement of the pendulum.
We cannot directly observe the phase of light, for this we need an interferometer.

Michelson interferometer: a laser beam is split into two equal parts by a beam splitter, reflected from movable mirrors, where it acquires phase with information about their displacement. After returning to the beam splitter, different phases of the beam interfere (the amplitudes are added or subtracted), and at the output we see a signal proportional to the displacement of the mirrors.
Not only gravitational wave detectors work on this principle, but also most of the sensors.
Unfortunately, in addition to the signal in such a detector, there will be many other noise sources.
I wrote about some of them in my article about the Einstein Telescope detector , but here I will limit myself to only two.
1. Thermal noise
Let's imagine a pendulum as a mirror suspended by a string.
The thermal Brownian motion of the molecules in this thread leads to excites the oscillations of the mirror. This movement is in principle random and can be represented as a force acting on the mirror at different frequencies. At frequencies close to the resonance of the pendulum, this force leads to a resonant increase in the displacement of the mirror. And although the spectrum of the thermal force is white (i.e. the force is the same at all frequencies), when measuring the spectrum of the mirror's motion, we will see a characteristic peak at the resonant frequency.
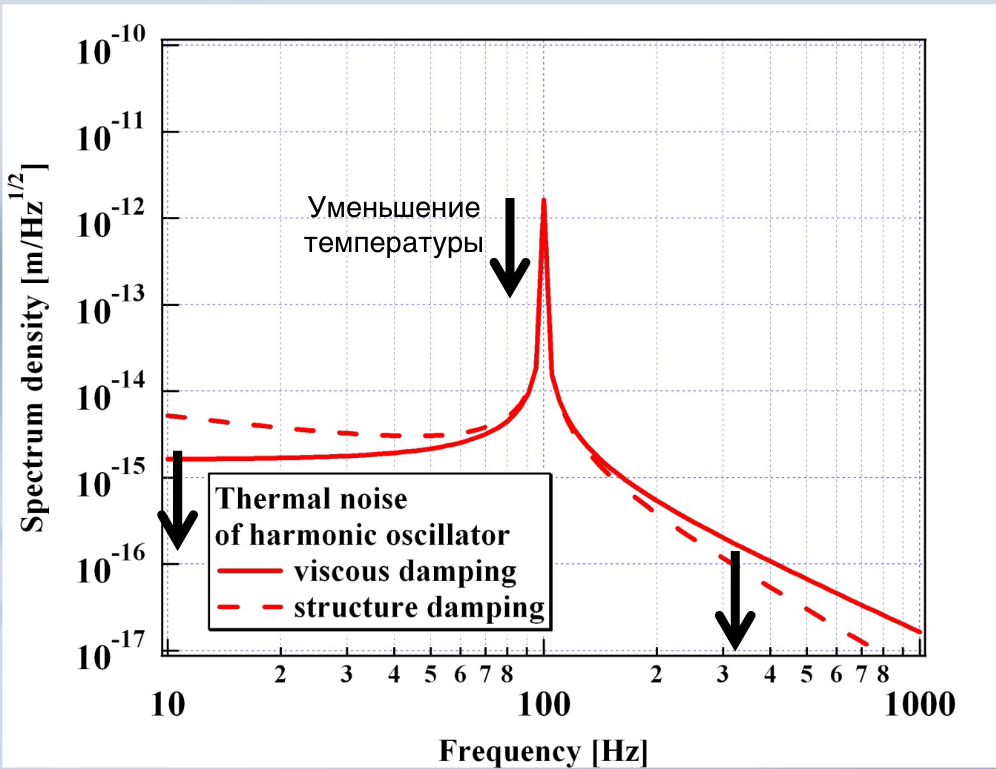
Thermal noise spectrum: displacement of the pendulum due to thermal noise at different frequencies. The lower the temperature, the less noise. Stolen from here .
Thermal noise depends on the temperature (the lower, the less noise) and on the quality of the thread (the amount of loss). Strictly speaking, there is a fluctuation-dissipation theorem that connects the observed noise with dissipation in the system.
Accordingly, in future gravitational wave detectors, this noise will be fought in two ways: by cooling the suspensions (and mirrors) and increasing their quality. In our experiment, we observed a thermal noise spectrum and reduced it using cooling, but more on that below.
2. Quantum shot noise
light has a quantum nature, individual photons fly with different random delays. In other words, the phase of the light beam turns out to be random.
When we try to measure the phase signal from an external force, it is limited by this phase uncertainty. On the detector, we see white spectrum noise, which turns out to be a fundamental limitation in measurement accuracy. All detectors are limited to shot noise. Despite its fundamental nature, quantum correlations can be used to reduce this noise.
To do this, you need to remember a little quantum mechanics. The phase uncertainty and the laser amplitude uncertainty are related by the Heisenberg relation:
In a conventional laser beam, these uncertainties are equal. However, it is possible to compress the phase uncertainty by increasing the amplitude uncertainty - the main thing is that their product satisfies the uncertainty relation. Such light is called G-degree compressed:
We'll use just such a trick to compress the phase uncertainty, allowing us to better observe the signal. By the way, gravitational wave detectors are already using squeezed light for all recent observations. Until recently, we did an experiment where we played with this squeezed light, and I wrote about it on Habré .
So, having figured out the basics, let's move on to the experiment.
2. Our interferometer
In our experiment, we used a small membrane with a side of 1 mm and a thickness of only 50 nm as a pendulum.


Left: photograph of the membrane (small window in the center of the gray frame). The membrane is stretched like a drum over a frame and vibrates inside. Right: illustration of membrane displacement.
Such a membrane oscillates at a frequency of about 400 kHz, and its Q factor (the number of oscillations before the loss of half the energy) is about 10 5 . To do this, however, you have to place it in a vacuum, otherwise the air presses on it too hard, and it does not vibrate.
It is also quite transparent: its reflectivity is only 20%.
This is not very convenient, because if such a membrane is used in a Michelson interferometer, most of the signal will be lost. Worse, when we want to use squeezed light, these quantum correlations are also lost, and they are especially sensitive to loss. So we decided to use a different configuration of the interferometer, "folding" the two arms of the Michelson interferometer so that the two mirrors turned out to be one - our membrane.
In such an interferometer, there are two modes: a part of the light passes through the membrane, and simply leaves the interferometer without carrying any signal (this is the Sagnac mode). The other part is reflected and acquires a phase proportional to the displacement of the membrane, and we receive a signal at the output of the interferometer.

Michelson-Sagnac interferometer
One of the main difficulties of the interferometer is its adjustment: the light must ideally overlap at the central beam splitter, otherwise interference does not happen, and we lose in sensitivity and in compressed light. This is especially difficult when the interferometer is inside a vacuum chamber or cryostat. To make the interferometer as stable as possible, we made it from a single block of material with a low coefficient of thermal expansion, optimizing its shape so that it does not bend when cooled. It was also coated with gold plating to isolate it from outside heat radiation as much as possible. We put this block into a cryostat, which could cool it down to 20K (-253C).
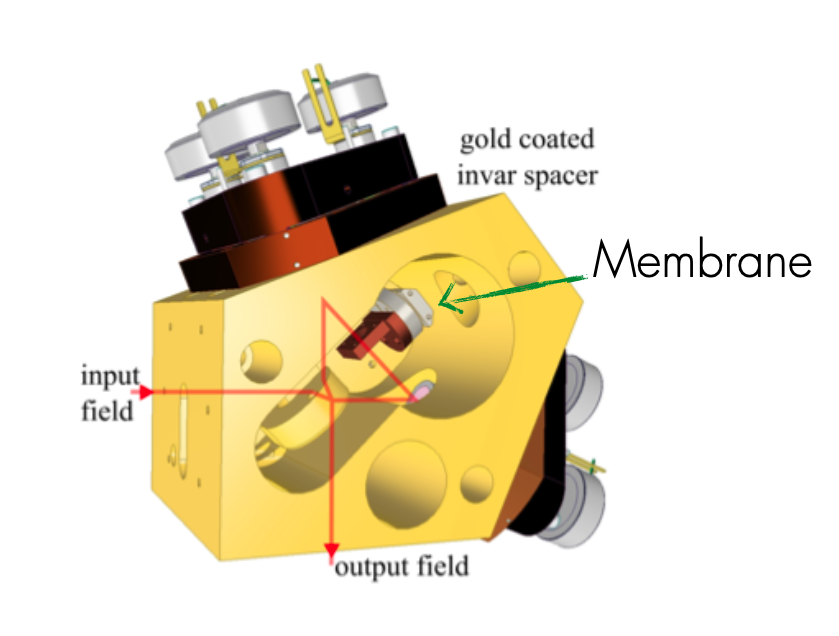
Schematic representation of an interferometer

Disassembled photograph of the interferometer: on the left - the interferometer and piezomotors displacing the mirrors at low temperatures. On the right is the membrane in the holder.
3. Compressed light
I recommend reading the article on Habré, which is an excellent introduction to the squeezed states of light.
Compressed light can be created in different ways, and we are using a non-linear crystal.
When a crystal is pumped with photons, a nonlinear process results in two photons from one pumping photon at half the energy (frequency) of the pumping photon. These photons find themselves in a quantum entangled state . The flux of such paired photons turns out to be more ordered than the flux of ordinary light, because shot noise is reduced - compression effect.
In this case, the phase uncertainty will be reduced, in the limit to zero, by increasing the amplitude uncertainty. You can do the opposite, reduce the amplitude uncertainty. In our experiments, we are not compressing the light itself, but quantum fluctuations of the zero state of the field (i.e., what is called vacuum fluctuations). In such a compressed vacuum, the average amplitude is zero and there is only phase and amplitude uncertainty.

. . () (). () : , . ( ). .
In the experiment, we first use a nonlinear process to create a pumping beam, reducing the wavelength from 1550nm to 775nm (SHG), and then use this pumping to compress vacuum fluctuations at a wavelength of 1550nm. Then we measure the resulting light in an interferometer, aligning it with a laser beam on a divider. This approach is called homodyne detection .

In this experiment, we had about 8.7 dB of compression at the input to the interferometer (noise reduction by 7.5 times), but in general we can do much stronger compression now - up to 30 times (15 dB). As I wrote above, compressed light is very susceptible to optical loss, and the improvement in sensitivity was not so significant (4.8dB).
Sample data

, - , . — .

, - , . — .
4. Putting it all together
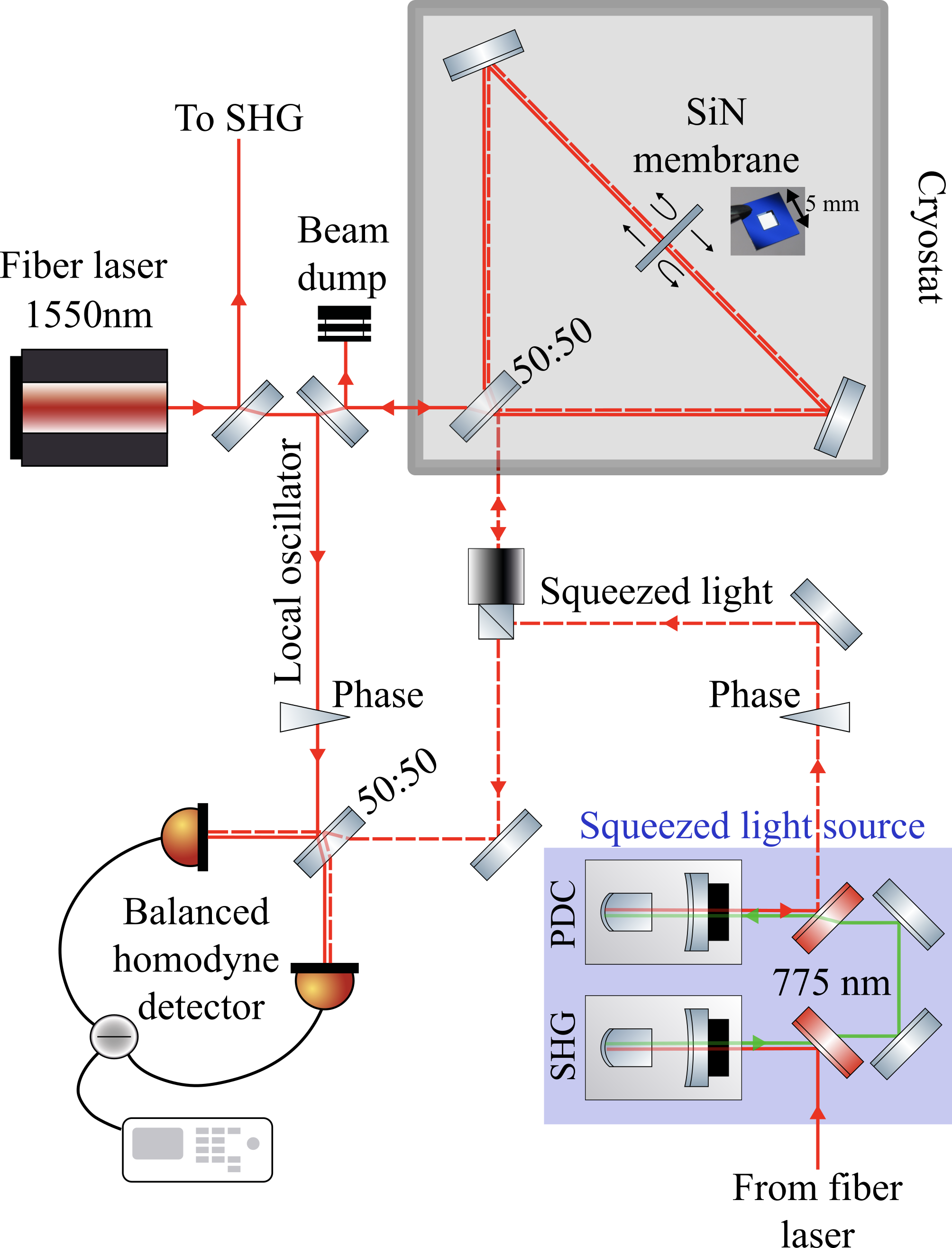
We send the compressed light into the interferometer from the signal port. It passes through the interferometer, and back out along with the signal from the movement of the membrane. Both are directed to a homodyne detector.
All phases of the light must be monitored: the resonators must remain in resonance with the main beam, the phases of the squeezed light must match the phases of the signal, the interferometer must remain correctly tuned, and the homodyne detector must measure the correct phase.
As a result, all together it occupies a large room:

More pictures




As a result, we were able to observe the thermal movement of our membrane and cool it down to 100K and up to 20K. This cooling could be directly observed in the spectrum of its motion: with decreasing temperature, the noise also decreased. On the other hand, we use compressed light and we suppress shot noise three times. The result is a prototype gravitational wave detector in which we combine a cooled interferometer with quantum compression for the first time.
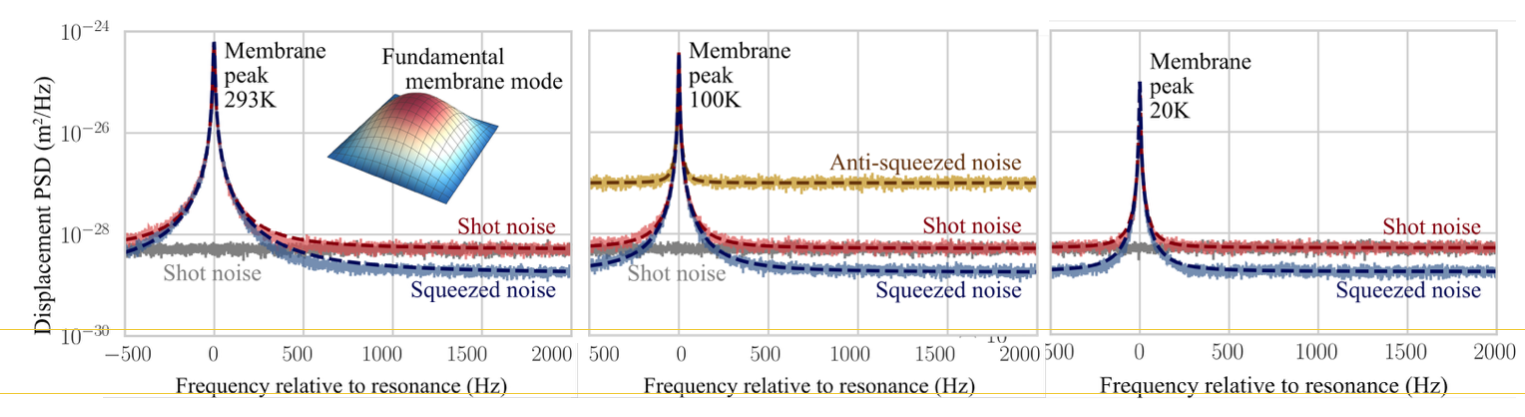
Most importantly, we demonstrate that it is possible to maintain the tuning of the interferometer when cooled to low temperatures and not introduce losses that would reduce the degree of quantum correlations in the system.
Most of the work was done by a graduate student in our laboratory (pictures are mostly taken from her dissertation). We went to this result for more than 6 years, and everything fits on 4 pages of the article. This is how we spend our time in quantum optics labs. Next time I'll tell you about another experiment and show more internals of optics and any hikporn.
Squeezed-light interferometry on a cryogenically-cooled micro-mechanical membrane
Last but not least, if you want to watch me as I try to figure out how to do scientific Twitter in English, welcome to @hbar_universe .