problem. The Goldbach problem is the statement that any even number, starting from 4, can be represented as the sum of two primes. That is, 6 = 3 + 3; 8 = 5 + 3 ... As I understand it, the solution to the problem is the proof or refutation of this statement.
The first thing we need to do is implement a method to check if a number is prime. A prime is a number that is divisible only by itself and by one.
public static bool IsPrimeNumber(ulong n)
{
var result = true;
if (n > 1)
{
for (ulong i = 2; i < n; i++)
{
if (n % i == 0)
{
result = false;
break;
}
}
}
else
{
result = false;
}
return result;
}
Now we need to get a collection of all primes up to ulong.MaxValue = 18446744073709551615 (2 ^ 64-1)
public static IEnumerable<ulong> GetAllPrimeNumbers(ulong maxNumber)
{
List<ulong> primeNumbers = new List<ulong>();
for (ulong i=0; i < maxNumber; i++ )
{
if (IsPrimeNumber(i))
{
primeNumbers.Add(i);
}
}
return primeNumbers;
}
Intuition suggests that it will take a very long time to calculate them, so we will reduce their number to 300,000
static void Main(string[] args)
{
Stopwatch stopwatch = new Stopwatch();
stopwatch.Start();
IEnumerable<ulong> primeNumbers = GetAllPrimeNumbers();
checkGoldbach(primeNumbers);
stopwatch.Stop();
Console.WriteLine(" " + stopwatch.Elapsed.TotalSeconds + " ");
foreach(var number in primeNumbers)
{
Console.Write(number + " ");
}
Console.ReadKey();
}

Then I wanted to find all the prime numbers up to 2 ^ 64 (It seemed to me that a couple of hours of calculations would be enough for me)
After two minutes of running the program, I decided to put a breakpoint and check which number is being checked for simplicity:
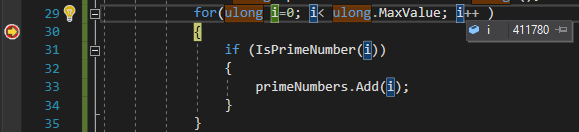
411780 iterations after two minutes of calculations. I decided to slightly optimize the method for checking the simplicity of a number, since there is no need to continue iterating after half of the number.
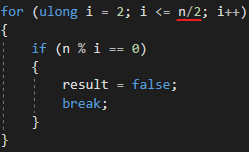
Thus, the number of iterations required to check the simplicity is halved. It seemed to me that in 2 minutes the number of iterations should double

But here, too, I was wrong. The productivity increased not by 100%, but by 22%. As I later understood, this is due to the fact that half of the checks, as before, are eliminated by dividing by 2, a third of all numbers not eliminated by dividing by 2 are eliminated by dividing by 3, etc. Of the 500,154 simplicity tests, 41549 primes were found. That is, the for iteration
for (ulong i = 2; i <= n/2; i++)
{
if (n % i == 0)
{
result = false;
break;
}
}
executed to the end (without break) only 41,549 times. In other cases, it was interrupted earlier ...
500154 and not nearly 2 ^ 64, you need to calculate how long it will take to check the simplicity of all numbers to 2 ^ 64
First, let's reduce the number of iterations from 2 ^ 64 to 30000 and calculate the running time of the stopwatch method

to iterate over numbers up to 30,000, 1 second was spent
now let's create a table with other values of the number of iterations
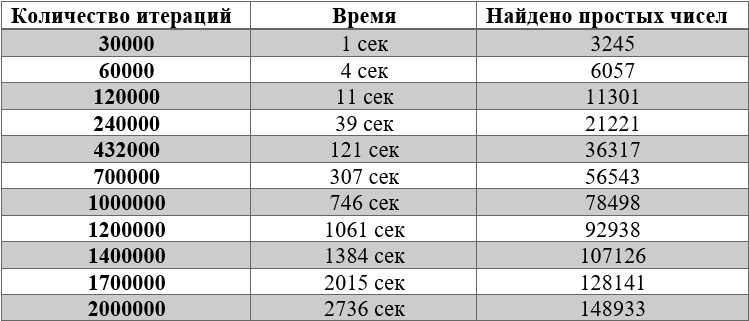
Let's write the result in Excel, and build a dot graph for the coordinates "Number of iterations for time" and "Number of primes per range"
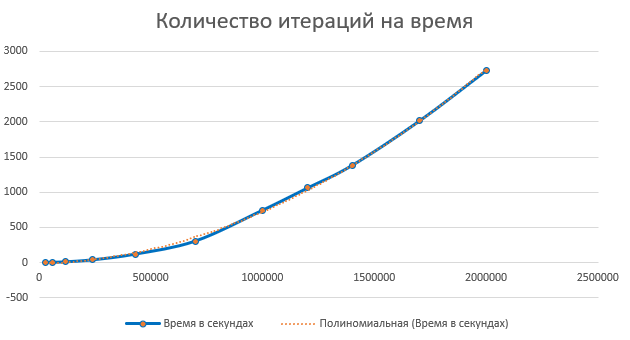
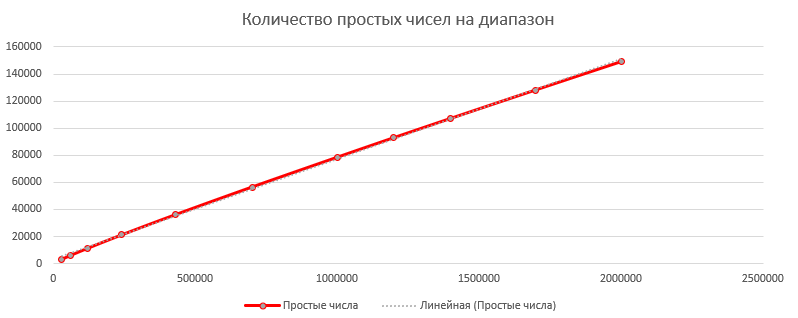
Now we can find out the approximate number of primes up to 2 ^ 64, and roughly how long it will take to find them all
If you add a "Linear" trend line to the "prime numbers per range" graph, Excel will give the formula y = 0.074x + 3004 (I have no idea how accurate the formula is). This means that the approximate number of primes up to ulong.MaxValue = 0.074 * 2 ^ 64 + 3004;
In the same way, adding the "Polynomial" trend line to the "Number of iterations over time" chart, we obtain the formula y = 7E-10x2 + 6E-05x. Substituting our number 2 ^ 64 instead of x, you can find out that to find all primes up to 2 ^ 64, we need approximately 2.38E + 29 seconds, or 7553198149564240000000 years. Ok, I can't expect that much.
Let's try to prove that Goldbach's conjecture is true for all even numbers up to 300,000.
public static void checkGoldbach(IEnumerable<ulong> primeNumbers)
{
ulong numbersCount = 300000;
for (ulong number = 4; number<numbersCount; number+=2)
{
bool isGoldbachResult = false;
foreach(ulong primeNumber1 in primeNumbers)
{
foreach(ulong primeNumber2 in primeNumbers)
{
if(primeNumber1+primeNumber2==number)
{
Console.WriteLine("{0} = {1} + {2}", number, primeNumber1, primeNumber2);
isGoldbachResult = true;
break;
}
if(primeNumber1+primeNumber2>number)
{
break;
}
}
if(isGoldbachResult|| primeNumber1>number)
{
break;
}
}
if(!isGoldbachResult)
{
Console.WriteLine(" " + number + " ");
break;
}
}
}
If Goldbach's statement is not true for some number, the method will stop computing at that number.
After 9 minutes of calculations, we can say that Goldbach's hypothesis is valid for numbers less than 300,000.
Total
Everything turned out to be not as simple as it seemed to me at the beginning, and I understand that I am not at all close to solving the problem.
Most likely, it seems to me that there are better options for checking a number for simplicity. It is possible that the method that checks even numbers for the correctness of Goldbach's statement can be implemented more rationally than a simple enumeration of primes, but I no longer want to spend so much time on this ...
Solving Goldbach's problem will give nothing to humanity. So far, it has been proven that the hypothesis is true for numbers up to 4 * 10 ^ 18, but what's the point of proving it for all numbers? For what purpose do mathematicians write books on this topic and generally spend their time solving such "problems"?
I really want to ask knowledgeable people whether my formula for calculating the number of prime numbers per range has a right to exist?
PS
Most likely, I do not need to write articles that I know little about. I didn't expect the community to react this way. But I didn’t pretend that my decision was the only correct one. I am an amateur in this field.
For what purpose did I write this article?
I took the time to research this question, and it seemed to me that some people might like it. It was interesting for me because it is a fun task. But why are mathematicians wasting their time on this? I sincerely don’t understand the real benefit of researching these specific questions.
PPS
After reading the reviews about the article, I decided to draw conclusions.
Most likely, it seems to me that there are better options for checking a number for simplicity
As suggested by users dvserg drWhy and Pavel_The_Bestit really is. For example, using the sieve of Eratosthenes, a collection of primes can be collected much faster. Here are articles that you can read on this topic: Algorithm for checking simplicity in O (log N) , Wikipedia , you can read the works of Srinivas Ramanujan Iyengor
Does my formula for calculating the number of prime numbers per range have the right to exist?
No
Solving Goldbach's Problem Will Give Nothing to Humanity?
My opinion that some math problems are useless caused a sharply negative attitude from most users. Usersvvadzim Refridgerator bromzh Graph-in Refridgerator EimKR bfDeveloper and yeawere able to convince me of this. I take my words back.
Since ancient times, mathematicians have been searching for truth, and their search often leads to beneficial consequences for progress. Perhaps the problem itself and its solution will not give the world anything here and now, but it is the conclusions drawn during the search for a solution that can be useful in the long term.