IBM has published the source code for the FHE toolkit for Linux on GitHub . The utilities run on IBM Z and x86 platforms and are supported by Ubuntu, Fedora, and CentOS.
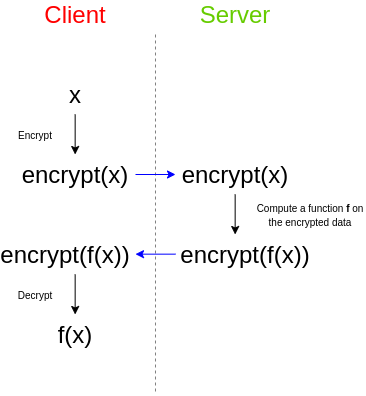
Fully Homomorphic Encryption (FHE) has long been considered something of the holy grail in cryptography. The task really seemed unrealistic. The FHE encryption type involves manipulation of encrypted data by a third party without the possibility of decrypting the data itself or the result of the manipulation.
How is this possible?
As a simple example, imagine you have a bunch of emails and want to use a third-party spam filter to check if they are spam. The spam filter works on the server because the developer tries to keep his algorithm confidential: either it hides the source code, or the spam filter depends on a very large database that they don't want to publicly disclose, as it makes the attack easier, or both other. It doesn't matter, the main thing is that the spam filter works on the server anyway - and you can't run it on your own. What to do in such a situation? You also care about the confidentiality of your data and do not want to transfer the content of e-mails to third parties in an open, unencrypted form. This is where fully homomorphic encryption comes to the rescue:
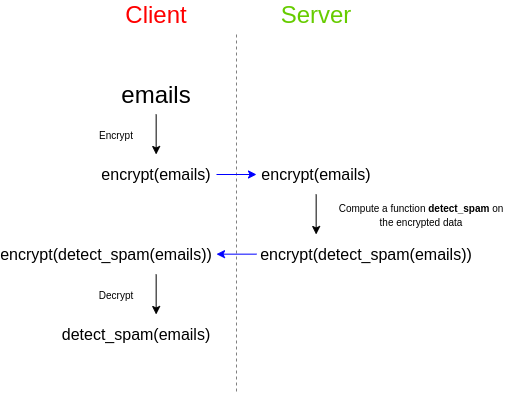
Thus, the service keeps the algorithm secret, and you keep your data secret. But FHE allows you to successfully apply the algorithm on this data, so that neither side learns the secrets of the other.
Fully homomorphic encryption has many uses, including in the blockchain, where the server can manipulate encrypted client data without disclosing the content of the information. That is, the server can fulfill the client's requests without knowing what it requested .
Other uses for homomorphic encryption:
- More efficient hidden address protocols and more general scalability solutions for privacy protocols, which today require each user to personally scan the entire blockchain for incoming transactions.
- , , .
- , ( , , , ).
In general, there are different kinds of homomorphic encryption, some more powerful than others. They differ in what operations can be performed with encrypted data.
Partially homomorphic encryption allows you to make only one operation with encrypted data, either addition or multiplication
partly homomorphic encryption (somewhat homomorphic) fully works only on a limited data set.
Finally, fully homomorphic encryption allows unlimited addition and multiplication operations on any data set.
Implementing partial homomorphic encryption is fairly easy: for example, multiplication is implemented in RSA:
, , so that
Elliptic curves offer a similar fold option. But to implement both addition and multiplication at the same time is much more difficult. The search for such a scheme has been going on since 1978, when Rivest, Adleman and Dertuzos formulated the problem and coined the term "homomorphic encryption". For 30 years, the existence of completely homomorphic systems has not been proven, and Rivest himself decided that the idea was not subject to implementation.
A major breakthrough came only in 2009 after the publication of the Ph.D. thesis of Stanford graduate student Craig Gentry. He described a possible construction of a completely homomorphic cryptosystem on ideal lattices . In his dissertation, he also proposed an innovative bootstrapping idea.... This trick turns the partial FHE scheme into a fully homomorphic encryption scheme. The bootstrapping method is shown in the diagram below. In short, here the bits of the private key are encrypted with the public key in a homomorphic scheme and published as a "booster key", which allows performing homomorphic encryption on the re-encrypted ciphertext, in which the noise is reduced to the original size. That is, we "refresh" the ciphertext, as if erasing the error of the old key.
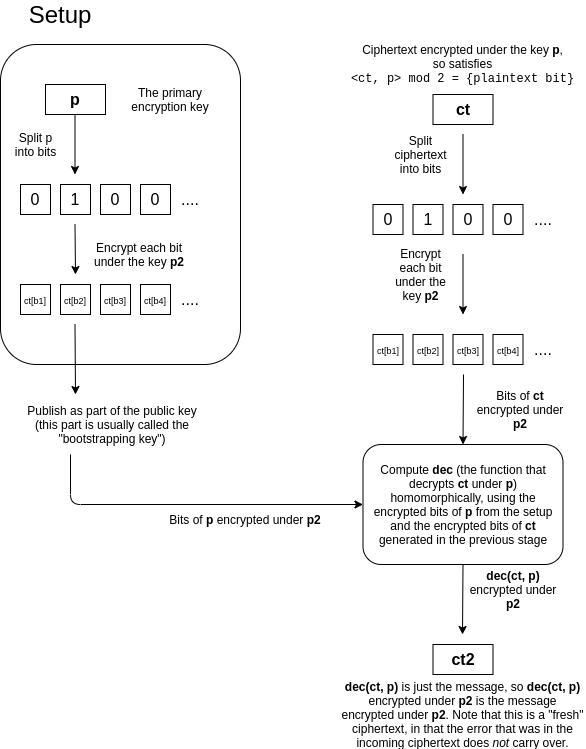
Simply put, the decryption procedure itself is a computation, therefore, it can be implemented as a homomorphic scheme that accepts ciphertext bits and bits of a secret key as input.
Gentry's cryptographic scheme was a major breakthrough, but introduced a new error that was independent of the amount of error in the original encryption. The author himself described a complex solution to the problem, but the improved scheme of Brakerski and Vaikuntanatan, proposed in 2011 (the scheme was called BGV (Brakerski-Gentry-Vaikuntanatan)) became more successful . In 2013, IBM released a free cryptographic library HELib with support for homomorphic encryption and BGV schemes In January 2020, HELib version 1.0.0 was released .
In 2013, Gentry again declared himself. With co-authors Sahai and Waters and presented a third generation full homomorphic encryption scheme - the GSW (Gentry, Sahai, Waters) scheme , which again uses lattice cryptography and boostrapping.
Over the years of development, a full-fledged set of tools with integrated samples for IDEs has been created on the basis of HELib, which work out of the box.
IBM has previously released fully homomorphic encryption tools for macOS and iOS . In the future, he promises to publish the source code of the version for Android.
The Linux version was released rather for demonstration purposes and works on a database with European countries and their capitals (the second example for the financial industry is fraud recognition by a neural network based on an encrypted base of anonymous transactions). So far, it has not come to the practical application of homomorphic encryption. According to theGentry himself in 2009, for example, processing a search query in Google in case the text is encrypted will require about a trillion times more calculations. Nevertheless, optimizations made by IBM have significantly improved the performance of the library, so that in a few years or decades, it may well find widespread use in web applications. IBM says the library can now run on IBM Z mainframes.