First, we will briefly familiarize ourselves with the methods of traversing graphs, write the actual pathfinding, and then move on to the most delicious one: optimizing performance and memory costs. Ideally, you should develop an implementation that does not generate garbage at all when used.
I was amazed when a superficial search did not give me a single good implementation of the A * algorithm in C # without using third-party libraries (this does not mean that there are none). So it's time to stretch your fingers!
I am waiting for a reader who wants to understand the work of pathfinding algorithms, as well as experts in algorithms to get acquainted with the implementation and methods of its optimization.
Let's get started!
An excursion into history
A two-dimensional mesh can be represented as a graph, where each of the vertices has 8 edges:
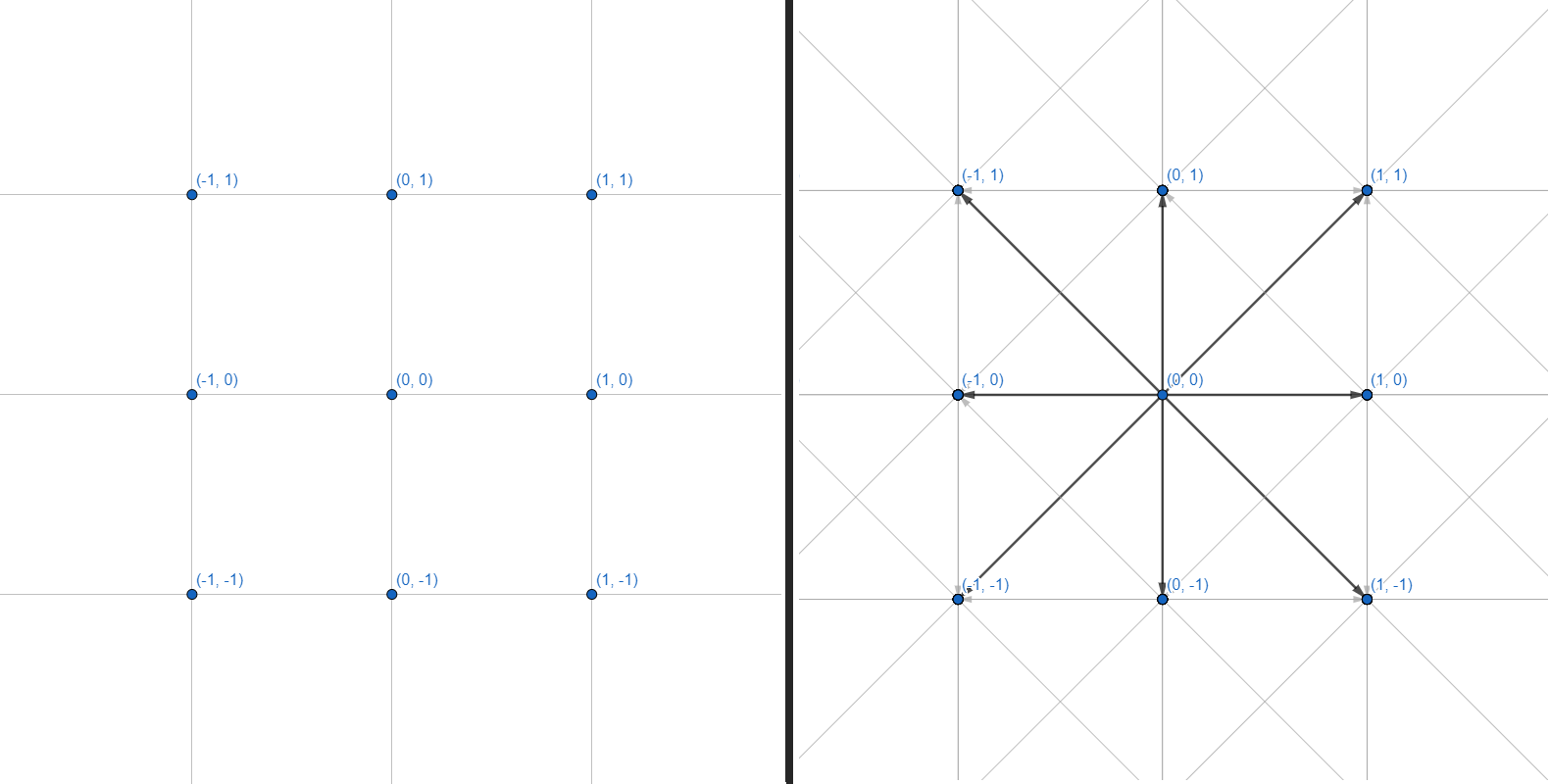
We will work with graphs. Each vertex is an integer coordinate. Each edge is a straight or diagonal transition between adjacent coordinates. We will not do the grid of coordinates and the calculation of the geometry of obstacles - we will restrict ourselves to an interface that accepts several coordinates as input and returns a set of points for building a path:
public interface IPath
{
IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles);
}To begin with, consider the existing methods for traversing the graph.
Depth search
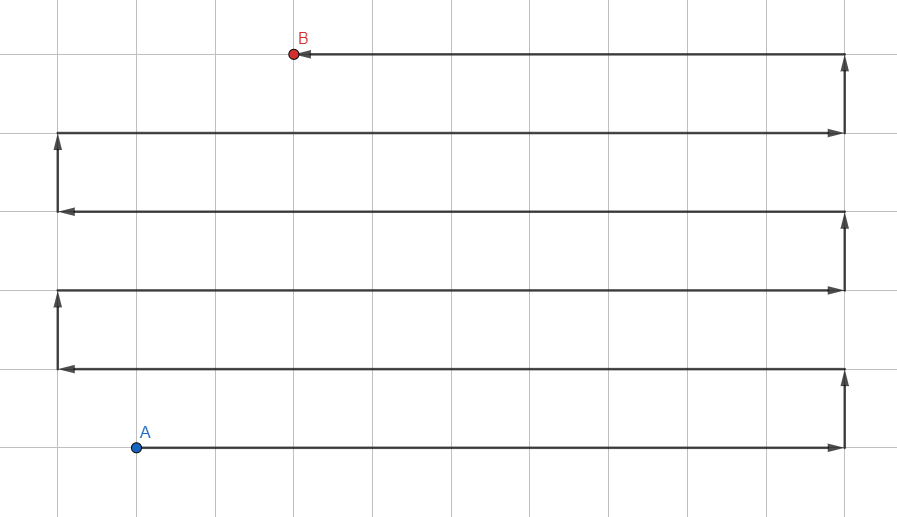
The simplest of the algorithms:
- Add all unvisited vertices near the current one to the stack.
- Move to the first vertex from the stack.
- If the vertex is the desired one, exit the cycle. If you come to a dead end, go back.
- GOTO 1.
It looks like this:
, Node , .
private Node DFS(Node first, Node target)
{
List<Node> visited = new List<Node>();
Stack<Node> frontier = new Stack<Node>();
frontier.Push(first);
while (frontier.Count > 0)
{
var current = frontier.Pop();
visited.Add(current);
if (current == target)
return Node;
var neighbours = current.GenerateNeighbours();
foreach(var neighbour in neighbours)
if (!visited.Contains(neighbour))
frontier.Push(neighbour);
}
return default;
}, Node , .
It is organized in the LIFO ( Last in - First out ) format , where newly added vertices are analyzed first. Each transition between the vertices must be monitored in order to build the actual path along the transitions.
This approach will never (well, almost) return the shortest path since it processes the graph in a random direction. It is more suitable for small graphs in order to determine without a headache whether there is at least some path to the desired vertex (for example, whether the desired link is present in the technology tree).
In the case of a navigation grid and infinite graphs, this search will endlessly go in one direction and waste computing resources, never reaching the desired point. This is solved by limiting the area in which the algorithm operates. We make it analyze only points located no further than N steps from the initial one. Thus, when the algorithm reaches the border of the region, it unfolds and continues to analyze the vertices within the specified radius.
Sometimes it is impossible to accurately determine the area, but you do not want to set the border at random. An iterative depth-first search comes to the rescue :
- Set the minimum area for DFS.
- Start search.
- If the path is not found, increase the search area by 1.
- GOTO 2.
The algorithm will run over and over again, each time covering a larger area until it finally finds the desired point.
It may seem like a waste of energy to re-run the algorithm at a slightly larger radius (anyway, most of the area has already been analyzed at the last iteration!), But no: the number of transitions between vertices grows geometrically with each increase in the radius. It will be much more expensive to take a radius larger than you need, than to walk several times along small radii.
It is easy for such a search to tighten a timer limit: it will search for a path with an expanding radius exactly until the specified time ends.
Breadth First Search
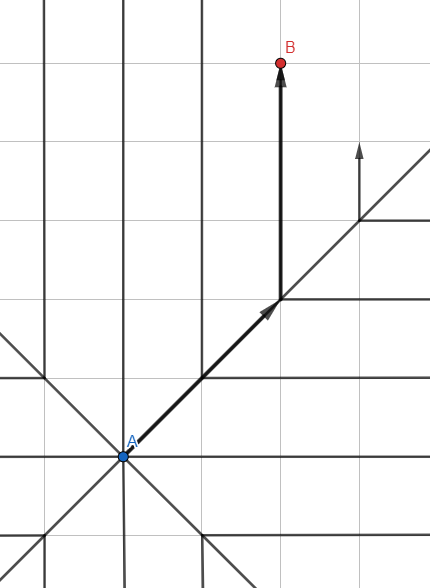
The illustration may resemble Jump Search - but this is the usual wave algorithm , and the lines represent the search propagation paths with the intermediate points removed.
In contrast to depth-first search using a stack (LIFO), let's take a queue (FIFO) to process the vertices:
- Add all unvisited neighbors to the queue.
- Go to the first vertex from the queue.
- If the vertex is the desired one, exit the cycle, otherwise GOTO 1.
It looks like this:
, Node , .
private Node BFS(Node first, Node target)
{
List<Node> visited = new List<Node>();
Queue<Node> frontier = new Queue<Node>();
frontier.Enqueue(first);
while (frontier.Count > 0)
{
var current = frontier.Dequeue();
visited.Add(current);
if (current == target)
return Node;
var neighbours = current.GenerateNeighbours();
foreach(var neighbour in neighbours)
if (!visited.Contains(neighbour))
frontier.Enqueue(neighbour);
}
return default;
}, Node , .
This approach gives the optimal path, but there is a catch: since the algorithm processes vertices in all directions, it works very slowly over long distances and graphs with strong branching. This is just our case.
Here, the area of operation of the algorithm cannot be limited, because in any case it will not go beyond the radius to the desired point. Other optimization methods are needed.
A *
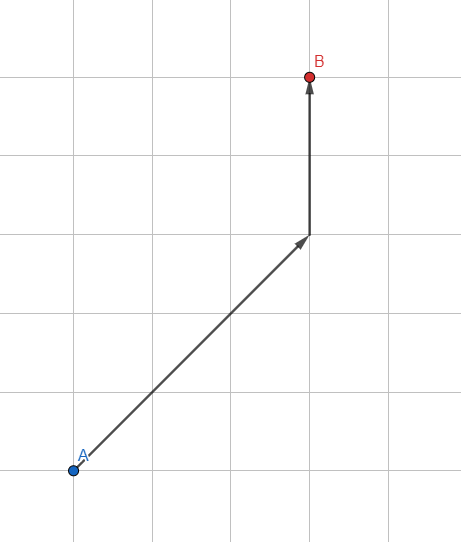
Let's modify the standard Breadth First Search: we use not a regular queue for storing vertices, but a sorted queue based on heuristics - an approximate estimate of the expected path.
How to estimate the expected path? The simplest is the length of the vector from the processed vertex to the desired point. The smaller the vector, the more promising the point and the closer to the beginning of the queue it becomes. The algorithm will give priority to those vertices that lie in the direction of the goal.
Thus, each iteration inside the algorithm will take a little longer due to additional calculations, but by reducing the number of vertices for analysis (only the most promising ones will be processed), we achieve a tremendous increase in the speed of the algorithm.
But there are still a lot of processed vertices. Finding the length of a vector is an expensive operation involving calculating the square root. Therefore, we will use a simplified calculation for the heuristic.
Let's create an integer vector:
public readonly struct Vector2Int : IEquatable<Vector2Int>
{
private static readonly double Sqr = Math.Sqrt(2);
public Vector2Int(int x, int y)
{
X = x;
Y = y;
}
public int X { get; }
public int Y { get; }
/// <summary>
/// Estimated path distance without obstacles.
/// </summary>
public double DistanceEstimate()
{
int linearSteps = Math.Abs(Math.Abs(Y) - Math.Abs(X));
int diagonalSteps = Math.Max(Math.Abs(Y), Math.Abs(X)) - linearSteps;
return linearSteps + Sqr * diagonalSteps;
}
public static Vector2Int operator +(Vector2Int a, Vector2Int b)
=> new Vector2Int(a.X + b.X, a.Y + b.Y);
public static Vector2Int operator -(Vector2Int a, Vector2Int b)
=> new Vector2Int(a.X - b.X, a.Y - b.Y);
public static bool operator ==(Vector2Int a, Vector2Int b)
=> a.X == b.X && a.Y == b.Y;
public static bool operator !=(Vector2Int a, Vector2Int b)
=> !(a == b);
public bool Equals(Vector2Int other)
=> X == other.X && Y == other.Y;
public override bool Equals(object obj)
{
if (!(obj is Vector2Int))
return false;
var other = (Vector2Int) obj;
return X == other.X && Y == other.Y;
}
public override int GetHashCode()
=> HashCode.Combine(X, Y);
public override string ToString()
=> $"({X}, {Y})";
}A standard structure for storing a pair of coordinates. Here we see the square root caching so that it can be computed only once. The IEquatable interface will allow us to compare vectors with each other without having to translate Vector2Int to object and back. This will greatly speed up our algorithm and get rid of unnecessary allocations.
DistanceEstimate () is used to estimate the approximate distance to the target by calculating the number of straight and diagonal transitions. An alternative way is common:
return Math.Max(Math.Abs(X), Math.Abs(Y))This option will work even faster, but this is compensated by the low accuracy of the diagonal distance estimation.
Now that we have a tool for working with coordinates, let's create an object that represents the top of the graph:
internal class PathNode
{
public PathNode(Vector2Int position, double traverseDist, double heuristicDist, PathNode parent)
{
Position = position;
TraverseDistance = traverseDist;
Parent = parent;
EstimatedTotalCost = TraverseDistance + heuristicDist;
}
public Vector2Int Position { get; }
public double TraverseDistance { get; }
public double EstimatedTotalCost { get; }
public PathNode Parent { get; }
}In Parent we will record the previous vertex for each new one: this will help in building the final path by points. In addition to the coordinates, we also save the distance traveled and the estimated cost of the path so that we can then select the most promising vertices for processing.
This class begs for improvement, but we'll come back to it later. For now, let's develop a method that generates the neighbors of the vertex:
internal static class NodeExtensions
{
private static readonly (Vector2Int position, double cost)[] NeighboursTemplate = {
(new Vector2Int(1, 0), 1),
(new Vector2Int(0, 1), 1),
(new Vector2Int(-1, 0), 1),
(new Vector2Int(0, -1), 1),
(new Vector2Int(1, 1), Math.Sqrt(2)),
(new Vector2Int(1, -1), Math.Sqrt(2)),
(new Vector2Int(-1, 1), Math.Sqrt(2)),
(new Vector2Int(-1, -1), Math.Sqrt(2))
};
public static IEnumerable<PathNode> GenerateNeighbours(this PathNode parent, Vector2Int target)
{
foreach ((Vector2Int position, double cost) in NeighboursTemplate)
{
Vector2Int nodePosition = position + parent.Position;
double traverseDistance = parent.TraverseDistance + cost;
double heuristicDistance = (position - target).DistanceEstimate();
yield return new PathNode(nodePosition, traverseDistance, heuristicDistance, parent);
}
}
}NeighborsTemplate - a predefined template for creating linear and diagonal neighbors of the desired point. It also takes into account the increased cost of diagonal transitions.
GenerateNeighbors - A generator that traverses the NeighborsTemplate and returns a new vertex for all eight adjacent sides.
It would be possible to shove the functionality inside the PathNode, but it feels like a slight violation of SRP. And I don't want to add third-party functionality inside the algorithm itself either: we will keep the classes as compact as possible.
Time to tackle the main pathfinding class!
public class Path
{
private readonly List<PathNode> frontier = new List<PathNode>();
private readonly List<Vector2Int> ignoredPositions = new List<Vector2Int>();
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles) {...}
private bool GenerateNodes(Vector2Int start, Vector2Int target,
IEnumerable<Vector2Int> obstacles, out PathNode node)
{
frontier.Clear();
ignoredPositions.Clear();
ignoredPositions.AddRange(obstacles);
// Add starting point.
frontier.Add(new PathNode(start, 0, 0, null));
while (frontier.Any())
{
// Find node with lowest estimated cost.
var lowest = frontier.Min(a => a.EstimatedTotalCost);
PathNode current = frontier.First(a => a.EstimatedTotalCost == lowest);
ignoredPositions.Add(current.Position);
if (current.Position.Equals(target))
{
node = current;
return true;
}
GenerateFrontierNodes(current, target);
}
// All nodes analyzed - no path detected.
node = null;
return false;
}
private void GenerateFrontierNodes(PathNode parent, Vector2Int target)
{
foreach (PathNode newNode in parent.GenerateNeighbours(target))
{
// Position is already checked or occupied by an obstacle.
if (ignoredPositions.Contains(newNode.Position)) continue;
// Node is not present in queue.
var node = frontier.FirstOrDefault(a => a.Position == newNode.Position);
if (node == null)
frontier.Add(newNode);
// Node is present in queue and new optimal path is detected.
else if (newNode.TraverseDistance < node.TraverseDistance)
{
frontier.Remove(node);
frontier.Add(newNode);
}
}
}
}GenerateNodes works with two collections: frontier, which contains a queue of vertices for analysis, and ignoredPositions, to which already processed vertices are added.
Each iteration of the loop finds the most promising vertex, checks if we have reached the end point, and generates new neighbors for this vertex.
And all this beauty fits into 50 lines.
It remains to implement the interface:
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles)
{
if (!GenerateNodes(start, target, obstacles, out PathNode node))
return Array.Empty<Vector2Int>();
var output = new List<Vector2Int>();
while (node.Parent != null)
{
output.Add(node.Position);
node = node.Parent;
}
output.Add(start);
return output.AsReadOnly();
}GenerateNodes returns us the final vertex, and since we wrote a parent neighbor to each of them, it is enough to walk through all the parents up to the initial vertex - and we get the shortest path. Everything is fine!
Or not?
Algorithm optimization
1. PathNode
Let's start simple. Let's simplify PathNode:
internal readonly struct PathNode
{
public PathNode(Vector2Int position, Vector2Int target, double traverseDistance)
{
Position = position;
TraverseDistance = traverseDistance;
double heuristicDistance = (position - target).DistanceEstimate();
EstimatedTotalCost = traverseDistance + heuristicDistance;
}
public Vector2Int Position { get; }
public double TraverseDistance { get; }
public double EstimatedTotalCost { get; }
}This is a common data wrapper that is also very often created. There is no reason to make it a class and load memory every time we write new . Therefore, we will use struct.
But there is a problem: structures cannot contain circular references to their own type. So, instead of storing the Parent inside the PathNode, we need another way to track the construction of paths between vertices. It's easy - let's add a new collection to the Path class:
private readonly Dictionary<Vector2Int, Vector2Int> links;And we slightly modify the generation of neighbors:
private void GenerateFrontierNodes(PathNode parent, Vector2Int target)
{
foreach (PathNode newNode in parent.GenerateNeighbours(target))
{
// Position is already checked or occupied by an obstacle.
if (ignoredPositions.Contains(newNode.Position)) continue;
// Node is not present in queue.
if (!frontier.TryGet(newNode.Position, out PathNode existingNode))
{
frontier.Enqueue(newNode);
links[newNode.Position] = parent.Position; // Add link to dictionary.
}
// Node is present in queue and new optimal path is detected.
else if (newNode.TraverseDistance < existingNode.TraverseDistance)
{
frontier.Modify(newNode);
links[newNode.Position] = parent.Position; // Add link to dictionary.
}
}
}Instead of writing the parent to the vertex itself, we write the transition to the dictionary. As a bonus, the dictionary can work directly with Vector2Int, and not with PathNode, since we only need coordinates and nothing else.
Generating the result inside Calculate is also simplified:
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles)
{
if (!GenerateNodes(start, target, obstacles))
return Array.Empty<Vector2Int>();
var output = new List<Vector2Int> {target};
while (links.TryGetValue(target, out target))
output.Add(target);
return output.AsReadOnly();
}2. NodeExtensions
Next, let's deal with the generation of neighbors. IEnumerable, for all its benefits, generates a sad amount of garbage in many situations. Let's get rid of it:
internal static class NodeExtensions
{
private static readonly (Vector2Int position, double cost)[] NeighboursTemplate = {
(new Vector2Int(1, 0), 1),
(new Vector2Int(0, 1), 1),
(new Vector2Int(-1, 0), 1),
(new Vector2Int(0, -1), 1),
(new Vector2Int(1, 1), Math.Sqrt(2)),
(new Vector2Int(1, -1), Math.Sqrt(2)),
(new Vector2Int(-1, 1), Math.Sqrt(2)),
(new Vector2Int(-1, -1), Math.Sqrt(2))
};
public static void Fill(this PathNode[] buffer, PathNode parent, Vector2Int target)
{
int i = 0;
foreach ((Vector2Int position, double cost) in NeighboursTemplate)
{
Vector2Int nodePosition = position + parent.Position;
double traverseDistance = parent.TraverseDistance + cost;
buffer[i++] = new PathNode(nodePosition, target, traverseDistance);
}
}
}Now our extension method is not a generator: it just fills the buffer that is passed to it as an argument. The buffer is stored as another collection inside the Path:
private const int MaxNeighbours = 8;
private readonly PathNode[] neighbours = new PathNode[MaxNeighbours];And it is used like this:
neighbours.Fill(parent, target);
foreach(var neighbour in neighbours)
{
// ...3. HashSet
Instead of using List, let's use HashSet:
private readonly HashSet<Vector2Int> ignoredPositions;It is much more efficient when working with large collections, the ignoredPositions.Contains () method is very resource-intensive due to the frequency of calls. A simple change of collection type will give a noticeable performance boost.
4. BinaryHeap
There is one place in our implementation that slows down the algorithm tenfold:
// Find node with lowest estimated cost.
var lowest = frontier.Min(a => a.EstimatedTotalCost);
PathNode current = frontier.First(a => a.EstimatedTotalCost == lowest);List itself is a bad choice, and using Linq makes things worse.
Ideally, we want a collection with:
- Automatic sorting.
- Low growth of asymptotic complexity.
- Fast insertion operation.
- Fast removal operation.
- Easy navigation through the elements.
SortedSet might seem like a good option, but it doesn't know how to contain duplicates. If we write sorting by EstimatedTotalCost, then all vertices with the same price (but different coordinates!) Will be eliminated. In open areas with a small number of obstacles, this is not terrible, plus it will speed up the algorithm, but in narrow mazes, the result will be inaccurate routes and false-negative results.
So we are implementing our collection - the binary heap ! The classic implementation satisfies 4 out of 5 requirements, and a small modification will make this collection ideal for our case.
The collection is a partially sorted tree with the complexity of insert and delete operations equal to log (n) .
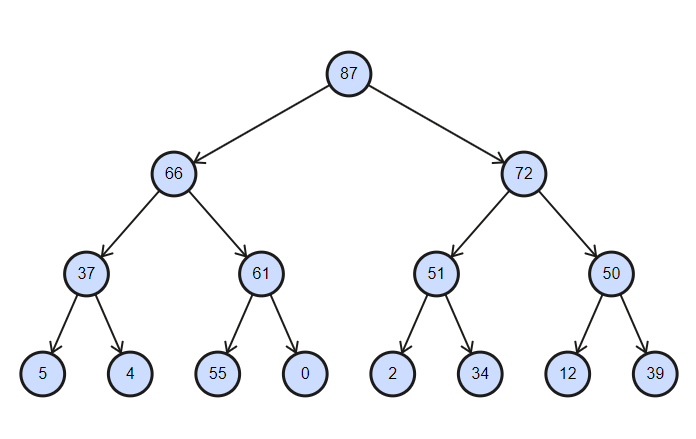
Binary heap sorted in descending order
internal interface IBinaryHeap<in TKey, T>
{
void Enqueue(T item);
T Dequeue();
void Clear();
bool TryGet(TKey key, out T value);
void Modify(T value);
int Count { get; }
}Let's write the easy part:
internal class BinaryHeap : IBinaryHeap<Vector2Int, PathNode>
{
private readonly IDictionary<Vector2Int, int> map;
private readonly IList<PathNode> collection;
private readonly IComparer<PathNode> comparer;
public BinaryHeap(IComparer<PathNode> comparer)
{
this.comparer = comparer;
collection = new List<PathNode>();
map = new Dictionary<Vector2Int, int>();
}
public int Count => collection.Count;
public void Clear()
{
collection.Clear();
map.Clear();
}
// ...
}We will use IComparer for custom sorting of vertices. IList is actually the vertex store that we will work with. We need IDictionary to keep track of the indices of the vertices for their quick removal (the standard implementation of the binary heap allows us to conveniently work with only the top element).
Let's add an element:
public void Enqueue(PathNode item)
{
collection.Add(item);
int i = collection.Count - 1;
map[item.Position] = i;
// Sort nodes from bottom to top.
while(i > 0)
{
int j = (i - 1) / 2;
if (comparer.Compare(collection[i], collection[j]) <= 0)
break;
Swap(i, j);
i = j;
}
}
private void Swap(int i, int j)
{
PathNode temp = collection[i];
collection[i] = collection[j];
collection[j] = temp;
map[collection[i].Position] = i;
map[collection[j].Position] = j;
}Each new element is added to the last cell of the tree, after which it is partially sorted from bottom to top: by nodes from the new element to the root, until the smallest element is as high as possible. Since not the entire collection is sorted, but only intermediate nodes between the top and the last, the operation has the complexity log (n) .
Getting an item:
public PathNode Dequeue()
{
if (collection.Count == 0) return default;
PathNode result = collection.First();
RemoveRoot();
map.Remove(result.Position);
return result;
}
private void RemoveRoot()
{
collection[0] = collection.Last();
map[collection[0].Position] = 0;
collection.RemoveAt(collection.Count - 1);
// Sort nodes from top to bottom.
var i = 0;
while(true)
{
int largest = LargestIndex(i);
if (largest == i)
return;
Swap(i, largest);
i = largest;
}
}
private int LargestIndex(int i)
{
int leftInd = 2 * i + 1;
int rightInd = 2 * i + 2;
int largest = i;
if (leftInd < collection.Count
&& comparer.Compare(collection[leftInd], collection[largest]) > 0)
largest = leftInd;
if (rightInd < collection.Count
&& comparer.Compare(collection[rightInd], collection[largest]) > 0)
largest = rightInd;
return largest;
}By analogy with adding: the root element is removed, and the last one is put in its place. Then a partial top-down sorting swaps the items so that the smallest one is at the top.
After that, we implement the search for an element and change it:
public bool TryGet(Vector2Int key, out PathNode value)
{
if (!map.TryGetValue(key, out int index))
{
value = default;
return false;
}
value = collection[index];
return true;
}
public void Modify(PathNode value)
{
if (!map.TryGetValue(value.Position, out int index))
throw new KeyNotFoundException(nameof(value));
collection[index] = value;
}There is nothing complicated here: we search for the index of the element through the dictionary, after which we access it directly.
Generic version of the heap:
internal class BinaryHeap<TKey, T> : IBinaryHeap<TKey, T> where TKey : IEquatable<TKey>
{
private readonly IDictionary<TKey, int> map;
private readonly IList<T> collection;
private readonly IComparer<T> comparer;
private readonly Func<T, TKey> lookupFunc;
public BinaryHeap(IComparer<T> comparer, Func<T, TKey> lookupFunc, int capacity)
{
this.comparer = comparer;
this.lookupFunc = lookupFunc;
collection = new List<T>(capacity);
map = new Dictionary<TKey, int>(capacity);
}
public int Count => collection.Count;
public void Enqueue(T item)
{
collection.Add(item);
int i = collection.Count - 1;
map[lookupFunc(item)] = i;
while(i > 0)
{
int j = (i - 1) / 2;
if (comparer.Compare(collection[i], collection[j]) <= 0)
break;
Swap(i, j);
i = j;
}
}
public T Dequeue()
{
if (collection.Count == 0) return default;
T result = collection.First();
RemoveRoot();
map.Remove(lookupFunc(result));
return result;
}
public void Clear()
{
collection.Clear();
map.Clear();
}
public bool TryGet(TKey key, out T value)
{
if (!map.TryGetValue(key, out int index))
{
value = default;
return false;
}
value = collection[index];
return true;
}
public void Modify(T value)
{
if (!map.TryGetValue(lookupFunc(value), out int index))
throw new KeyNotFoundException(nameof(value));
collection[index] = value;
}
private void RemoveRoot()
{
collection[0] = collection.Last();
map[lookupFunc(collection[0])] = 0;
collection.RemoveAt(collection.Count - 1);
var i = 0;
while(true)
{
int largest = LargestIndex(i);
if (largest == i)
return;
Swap(i, largest);
i = largest;
}
}
private void Swap(int i, int j)
{
T temp = collection[i];
collection[i] = collection[j];
collection[j] = temp;
map[lookupFunc(collection[i])] = i;
map[lookupFunc(collection[j])] = j;
}
private int LargestIndex(int i)
{
int leftInd = 2 * i + 1;
int rightInd = 2 * i + 2;
int largest = i;
if (leftInd < collection.Count && comparer.Compare(collection[leftInd], collection[largest]) > 0) largest = leftInd;
if (rightInd < collection.Count && comparer.Compare(collection[rightInd], collection[largest]) > 0) largest = rightInd;
return largest;
}
}Now our pathfinding has a decent speed, and there is almost no garbage generation left. The finish is near!
5. Reusable collections
The algorithm is being developed with an eye to the ability to call it dozens of times per second. Generation of any garbage is categorically unacceptable: a loaded garbage collector can (and will!) Cause periodic drawdowns in performance.
All collections, except for output, are already declared once when the class is created, and the last one is also added there:
private const int MaxNeighbours = 8;
private readonly PathNode[] neighbours = new PathNode[MaxNeighbours];
private readonly IBinaryHeap<Vector2Int, PathNode> frontier;
private readonly HashSet<Vector2Int> ignoredPositions;
private readonly IList<Vector2Int> output;
private readonly IDictionary<Vector2Int, Vector2Int> links;
public Path()
{
var comparer = Comparer<PathNode>.Create((a, b) => b.EstimatedTotalCost.CompareTo(a.EstimatedTotalCost));
frontier = new BinaryHeap(comparer);
ignoredPositions = new HashSet<Vector2Int>();
output = new List<Vector2Int>();
links = new Dictionary<Vector2Int, Vector2Int>();
}The public method takes the following form:
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles)
{
if (!GenerateNodes(start, target, obstacles))
return Array.Empty<Vector2Int>();
output.Clear();
output.Add(target);
while (links.TryGetValue(target, out target))
output.Add(target);
return output.AsReadOnly();
}And it's not just about creating collections! Collections dynamically change their capacity when filled; if the path is long, resizing will occur dozens of times. This is very memory intensive. When we clear the collections and reuse them without declaring new ones, they retain their capacity. The first path construction will create a lot of garbage when initializing collections and changing their capacities, but subsequent calls will work fine without any allocations (provided that the length of each computed path is plus or minus the same without sharp distortions). Hence the next point:
6. (Bonus) Announcement of the size of collections
A number of questions immediately arise:
- Is it better to offload the load to the constructor of the Path class or leave it on the first call to the pathfinder?
- What capacity to feed the collections?
- Is it cheaper to announce a larger capacity right away or let the collection expand on its own?
The third can be answered right away: if we have hundreds and thousands of cells for finding a path, it will definitely be cheaper to immediately assign a certain size to our collections.
The other two questions are more difficult to answer. The answer to these needs to be determined empirically for each use case. If we still decide to move the load into the constructor, then it's time to add a limit on the number of steps to our algorithm:
public Path(int maxSteps)
{
this.maxSteps = maxSteps;
var comparer = Comparer<PathNode>.Create((a, b) => b.EstimatedTotalCost.CompareTo(a.EstimatedTotalCost));
frontier = new BinaryHeap(comparer, maxSteps);
ignoredPositions = new HashSet<Vector2Int>(maxSteps);
output = new List<Vector2Int>(maxSteps);
links = new Dictionary<Vector2Int, Vector2Int>(maxSteps);
}Inside GenerateNodes, correct the loop:
var step = 0;
while (frontier.Count > 0 && step++ <= maxSteps)
{
// ...
}Thus, collections are immediately assigned a capacity equal to the maximum path. Some collections contain not only the traversed nodes, but also their neighbors: for such collections, you can use a capacity 4-5 times larger than the specified one.
It may seem a bit too much, but for paths close to the declared maximum, assignment of the size of collections spends half to three times less memory than dynamic expansion. On the other hand, if you assign very large values to the maxSteps value and generate short paths, this innovation will only harm. Oh, and you shouldn't try to use int.MaxValue!
The optimal solution would be to create two constructors, one of which sets the initial capacity of the collections. Then our class can be used in both cases without modifying it.
What else can you do?
- .
- XML-.
- GetHashCode Vector2Int. , , , .
- , . .
- IComparable PathNode EqualityComparer. .
- : , . , , .
- Change the method signature in our interface to better reflect its essence:
bool Calculate(Vector2Int start, Vector2Int target, IReadOnlyCollection<Vector2Int> obstacles, out IReadOnlyCollection<Vector2Int> path);
Thus, the method clearly shows the logic of its operation, while the original method should have been called like this: CalculateOrReturnEmpty .
The final version of the Path class:
/// <summary>
/// Reusable A* path finder.
/// </summary>
public class Path : IPath
{
private const int MaxNeighbours = 8;
private readonly PathNode[] neighbours = new PathNode[MaxNeighbours];
private readonly int maxSteps;
private readonly IBinaryHeap<Vector2Int, PathNode> frontier;
private readonly HashSet<Vector2Int> ignoredPositions;
private readonly List<Vector2Int> output;
private readonly IDictionary<Vector2Int, Vector2Int> links;
/// <summary>
/// Creation of new path finder.
/// </summary>
/// <exception cref="ArgumentOutOfRangeException"></exception>
public Path(int maxSteps = int.MaxValue, int initialCapacity = 0)
{
if (maxSteps <= 0)
throw new ArgumentOutOfRangeException(nameof(maxSteps));
if (initialCapacity < 0)
throw new ArgumentOutOfRangeException(nameof(initialCapacity));
this.maxSteps = maxSteps;
var comparer = Comparer<PathNode>.Create((a, b) => b.EstimatedTotalCost.CompareTo(a.EstimatedTotalCost));
frontier = new BinaryHeap<Vector2Int, PathNode>(comparer, a => a.Position, initialCapacity);
ignoredPositions = new HashSet<Vector2Int>(initialCapacity);
output = new List<Vector2Int>(initialCapacity);
links = new Dictionary<Vector2Int, Vector2Int>(initialCapacity);
}
/// <summary>
/// Calculate a new path between two points.
/// </summary>
/// <exception cref="ArgumentNullException"></exception>
public bool Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles,
out IReadOnlyCollection<Vector2Int> path)
{
if (obstacles == null)
throw new ArgumentNullException(nameof(obstacles));
if (!GenerateNodes(start, target, obstacles))
{
path = Array.Empty<Vector2Int>();
return false;
}
output.Clear();
output.Add(target);
while (links.TryGetValue(target, out target)) output.Add(target);
path = output;
return true;
}
private bool GenerateNodes(Vector2Int start, Vector2Int target, IReadOnlyCollection<Vector2Int> obstacles)
{
frontier.Clear();
ignoredPositions.Clear();
links.Clear();
frontier.Enqueue(new PathNode(start, target, 0));
ignoredPositions.UnionWith(obstacles);
var step = 0;
while (frontier.Count > 0 && step++ <= maxSteps)
{
PathNode current = frontier.Dequeue();
ignoredPositions.Add(current.Position);
if (current.Position.Equals(target)) return true;
GenerateFrontierNodes(current, target);
}
// All nodes analyzed - no path detected.
return false;
}
private void GenerateFrontierNodes(PathNode parent, Vector2Int target)
{
neighbours.Fill(parent, target);
foreach (PathNode newNode in neighbours)
{
// Position is already checked or occupied by an obstacle.
if (ignoredPositions.Contains(newNode.Position)) continue;
// Node is not present in queue.
if (!frontier.TryGet(newNode.Position, out PathNode existingNode))
{
frontier.Enqueue(newNode);
links[newNode.Position] = parent.Position;
}
// Node is present in queue and new optimal path is detected.
else if (newNode.TraverseDistance < existingNode.TraverseDistance)
{
frontier.Modify(newNode);
links[newNode.Position] = parent.Position;
}
}
}
}Link to source code