
Over the past three years, Nvidia has been creating graphics chips in which, in addition to the usual cores used for shaders, additional ones are installed. These cores, called tensor cores, are already found in thousands of desktops, laptops, workstations and data centers around the world. But what do they do and what are they used for? Are they even needed in graphics cards?
Today we will explain what a tensor is and how tensor kernels are used in the graphics and deep learning world.
A short math lesson
To understand what tensor kernels are doing and what they can be used for, we first figure out what tensors are. All microprocessors, no matter what task they perform, perform mathematical operations on numbers (addition, multiplication, etc.).
Sometimes these numbers need to be grouped because they have a certain meaning for each other. For example, when the chip processes data to render graphics, it can deal with single integer values (say +2 or +115) as the scaling factor, or with a group of floating point numbers (+0.1, -0.5, +0.6) as coordinates of a point in 3D space. In the second case, all three data items are required for the point position.
TensorIs a mathematical object that describes the relationships between other mathematical objects related to each other. They are usually displayed as an array of numbers, the dimensions of which are shown below.

The simplest tensor type has dimension zero and consists of a single value; otherwise, it is called a scalar . As the number of dimensions increases, we encounter other common mathematical structures:
- 1 dimension = vector
- 2 dimensions = matrix
Strictly speaking, a scalar is a tensor 0 x 0, a vector is 1 x 0, and a matrix is 1 x 1, but for the sake of simplicity and reference to the tensor cores of the GPU, we will consider tensors only in the form of matrices.
One of the most important mathematical operations performed on matrices is multiplication (or product). Let's take a look at how two matrices with four rows and columns of data are multiplied by each other:
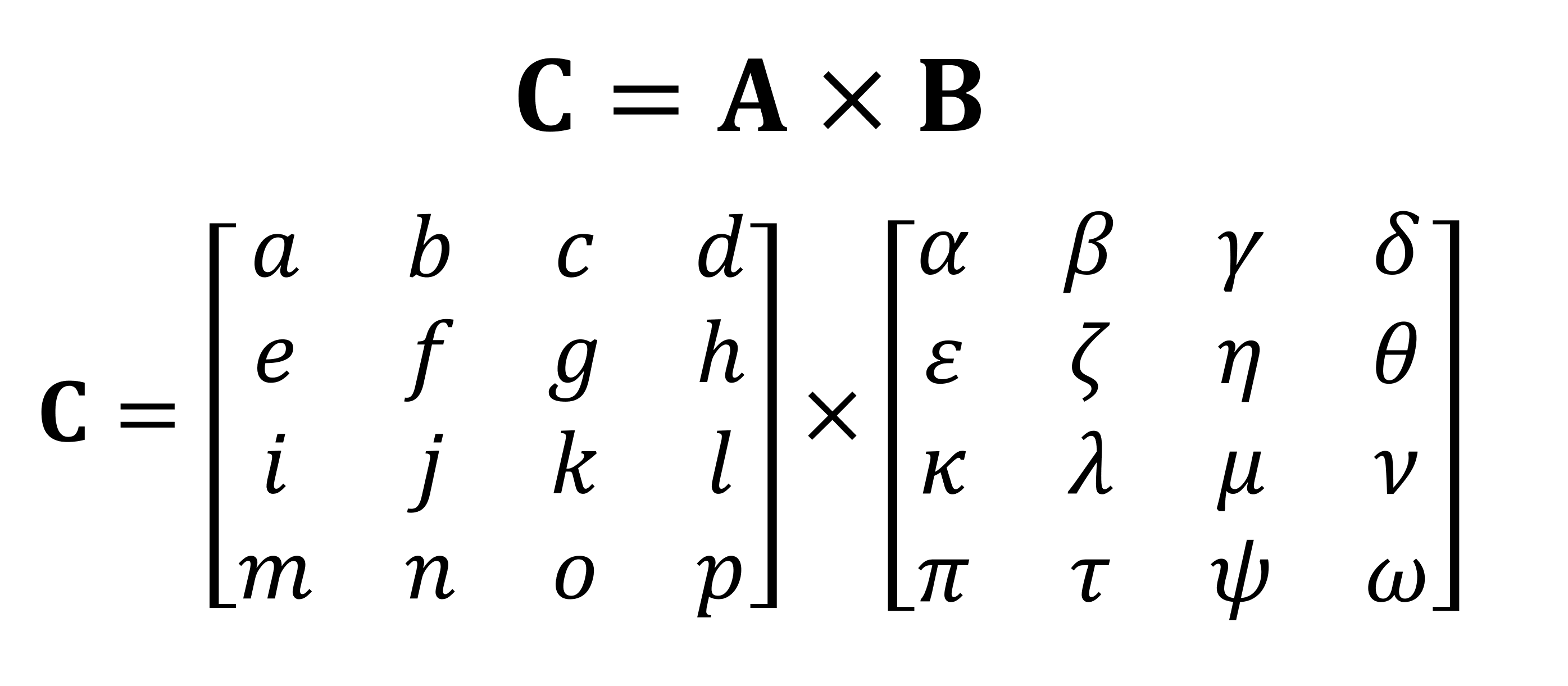
The final result of multiplication will always be the same number of rows as in the first matrix and the same number of columns as in the second. How do you multiply these two arrays? Like this:
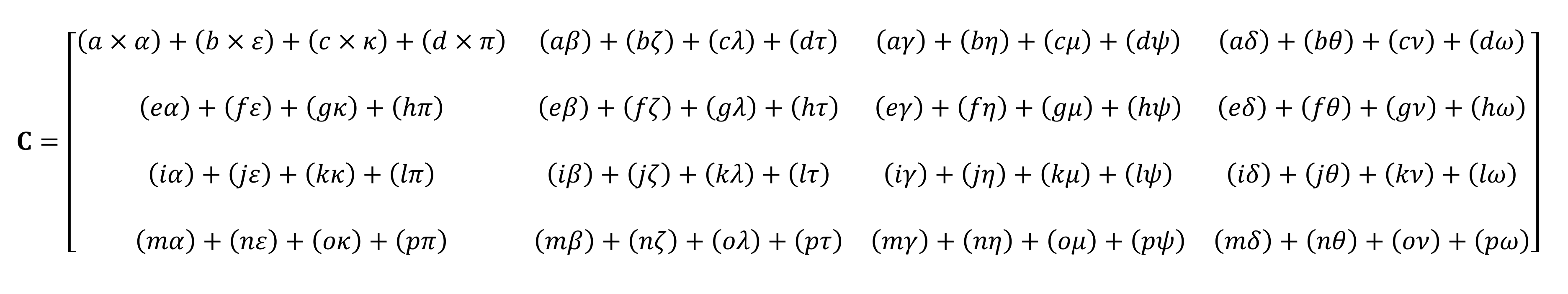
It will not be possible to count it on the fingers
As you can see, the calculation of the "simple" product of matrices consists of a whole bunch of small multiplications and additions. Since any modern central processing unit can perform both of these operations, the simplest tensors can be performed by every desktop, laptop or tablet.
However, the example shown above contains 64 multiplications and 48 additions; each small product gives a value that needs to be stored somewhere before it can be added to the other three small products so that the final tensor value can be stored later. Therefore, despite the mathematical simplicity of matrix multiplications, they are computationally expensive. - it is necessary to use a lot of registers, and the cache must be able to cope with a bunch of read and write operations.

Intel Sandy Bridge architecture, which first introduced AVX extensions
Over the years, AMD and Intel processors have had various extensions (MMX, SSE, and now AVX - all of which are SIMD, single instruction multiple data ), allowing the processor to simultaneously process many numbers floating point; this is exactly what is required for matrix multiplication.
But there is a special type of processor that is specifically designed to handle SIMD operations: the graphics processing unit (GPU).
Smarter than a regular calculator?
In the world of graphics, it is necessary to simultaneously transmit and process huge amounts of information in the form of vectors. Due to their parallel processing capability, GPUs are ideal for tensor processing; all modern GPUs support a functionality called GEMM ( General Matrix Multiplication ).
This is a "glued" operation in which two matrices are multiplied and the result is then accumulated with another matrix. There are important restrictions on the format of matrices, and they are all related to the number of rows and columns of each matrix.

GEMM row and column requirements: matrix A (mxk), matrix B (kxn), matrix C (mxn)
The algorithms used to perform operations on matrices usually work best when matrices are square (for example, a 10 x 10 array will work better than 50 x 2) and rather small in size. But they will still perform better if processed on equipment that is exclusively designed for such operations.
In December 2017, Nvidia released a graphics card with a GPU featuring the new Volta architecture . It was aimed at professional markets, so this chip was not used in GeForce models. It was unique because it became the first GPU with cores only for performing tensor calculations.

An Nvidia Titan V graphics card with a GV100 Volta chip. Yes, you can run Crysis on it Nvidia's
tensor cores were designed to execute 64 GEMMs per clock cycle with 4 x 4 matrices containing FP16 values (floating point numbers of 16 bits) or FP16 multiplication with FP32 addition. Such tensors are very small in size, so when processing real sets of data, the kernels process small parts of large matrices, building the final answer.
Less than a year later, Nvidia released the Turing architecture . This time, tensor cores were also installed in the GeForce modelconsumer level. The system was improved to support other data formats, such as INT8 (8-bit integer value), but otherwise they worked the same as in Volta.

Earlier this year, the Ampere architecture debuted in the A100 data center GPU , and this time Nvidia improved performance (256 GEMM per cycle instead of 64), added new data formats, and the ability to process very fast sparse tensor (matrixes with many zeros).
Programmers can access the tensor cores of Volta, Turing and Ampere chips very easily: the code only needs to use a flag telling the API and drivers to use tensor cores, the data type must be supported by the cores, and the matrix dimensions must be multiples of 8. When executed All these conditions will be taken care of by the equipment.
That's all great, but how much better are Tensor Cores at processing GEMM than regular GPU cores?
When the Volta came out, Anandtech ran math tests on three Nvidia cards: the new Volta, the most powerful of the Pascal lineup, and the old Maxwell card.
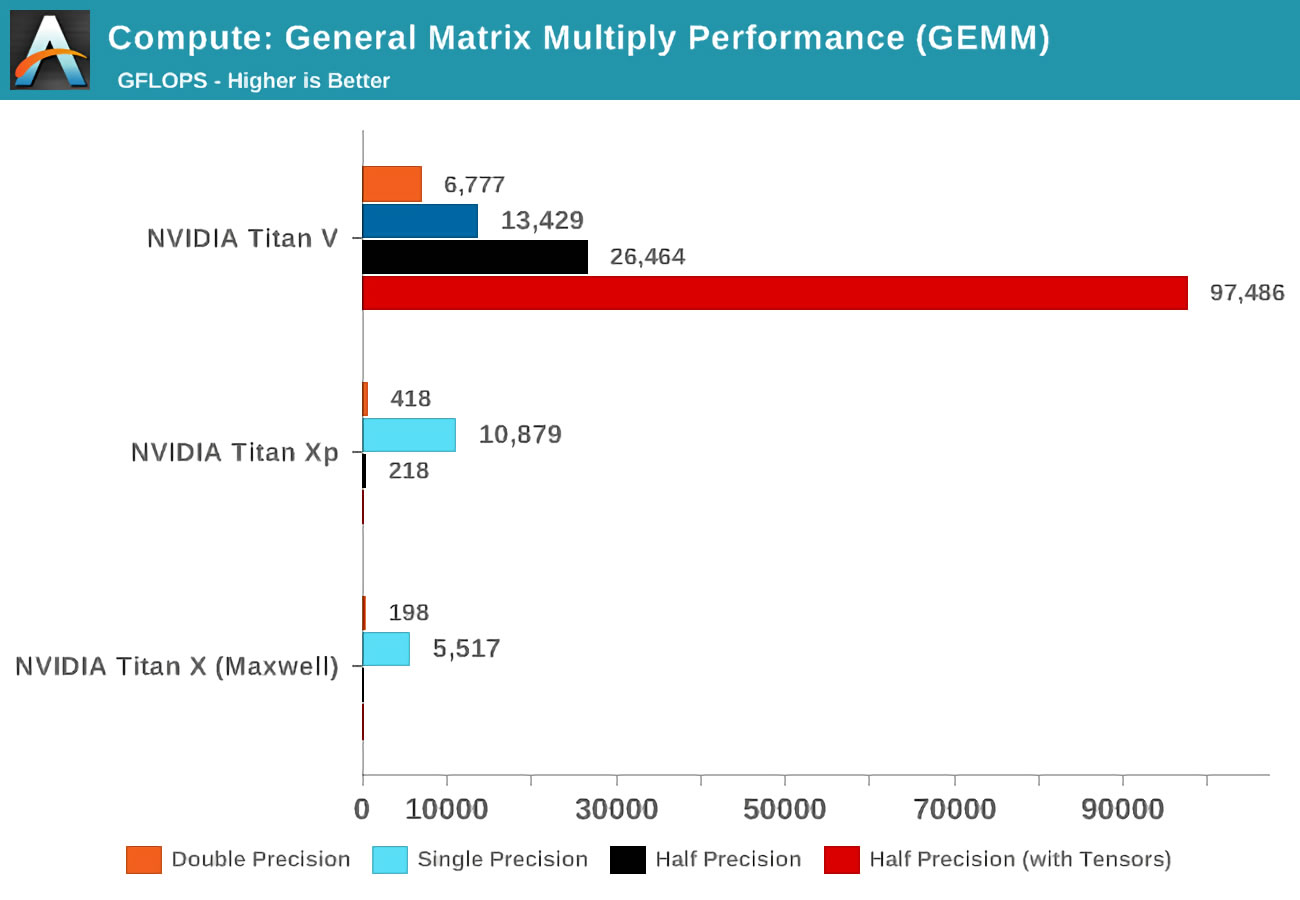
The concept of accuracy (precision) refers to the number of bits used for floating-point numbers in the matrices: double (double) denotes 64, a single (single) - 32, and so on. The horizontal axis is the maximum number of floating point operations performed per second, or FLOPs for short (remember that one GEMM is 3 FLOPs).
Just take a look at the results when using tensor kernels instead of the so called CUDA kernels! Obviously, they are amazing at this job, but what can we do with tensor kernels?
The math that makes everything better
Tensor computing is extremely useful in physics and engineering, it is used to solve all sorts of complex problems in fluid mechanics , electromagnetism and astrophysics , however the computers that were used to process such numbers usually performed matrix operations in large clusters from central processing units.
Another area in which tensors are popular is machine learning , especially its subsection "deep learning". Its meaning boils down to processing huge datasets in giant arrays called neural networks . Connections between different data values are assigned a certain weight - a number that expresses the importance of a particular connection.
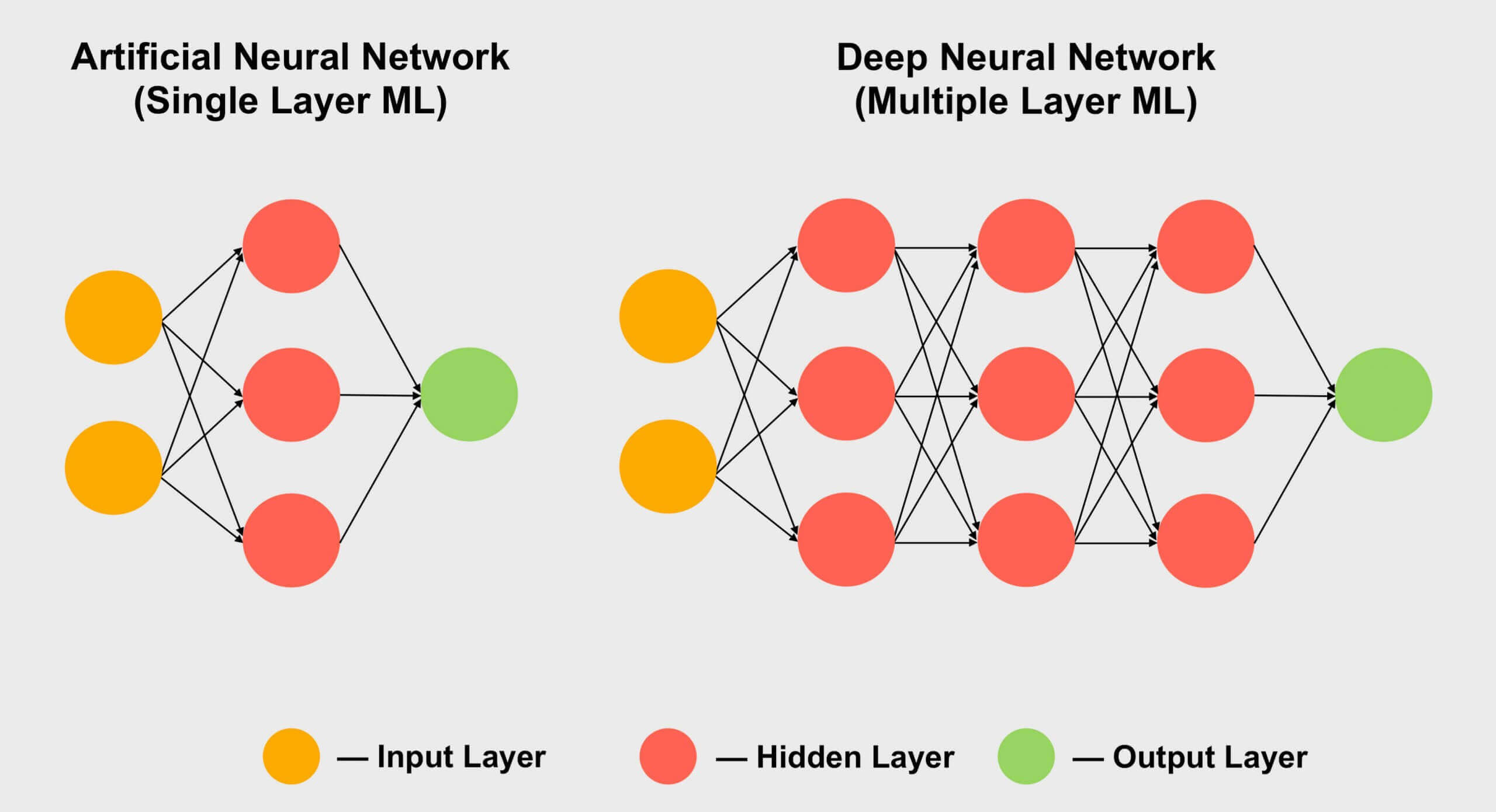
So when we need to figure out how all these hundreds, if not thousands of connections interact, we need to multiply every piece of data in the network by all possible connection weights. In other words, multiply two matrices, which is classical tensor mathematics!

Water-cooled Google TPU 3.0 Chips
This is why all deep learning supercomputers use GPUs, and almost always Nvidia. However, some companies have even developed their own processors from tensor cores. Google, for example, announced the development of its first TPU ( tensor processing unit ) in 2016 , but these chips are so specialized that they cannot do anything other than operations with matrices.
Tensor cores in consumer GPUs (GeForce RTX)
But what if I buy an Nvidia GeForce RTX graphics card, not being an astrophysicist solving Riemannian manifold problems, or an expert experimenting with convolutional neural network depths ...? How can I use tensor kernels?
More often than not, they don't apply to regular video rendering, encoding, or decoding, so it might seem like you've wasted money on a useless feature. However, Nvidia has built tensor cores into its consumer products in 2018 (Turing GeForce RTX) while implementing DLSS - Deep Learning Super Sampling .

The principle is simple: render the frame at a fairly low resolution, and after completion, increase the resolution of the final result so that it matches the "native" screen dimensions of the monitor (for example, render at 1080p, and then resize to 1400p). This improves performance because fewer pixels are processed and the screen still produces a beautiful image.
Consoles have had this feature for years, and many modern PC games provide this feature as well. In Assassin's Creed: Odyssey from Ubisoft, you can reduce the render resolution to as little as 50% of the monitor resolution. Unfortunately, the results don't look so pretty. This is what the game looks like in 4K with maximum graphics settings:

Textures look nicer at high resolutions because they retain more detail. However, it takes a lot of processing to display these pixels on screen. Now take a look at what happens when the render is set to 1080p (25% of the previous number of pixels), using the shaders at the end to stretch the image to 4K.

Due to the jpeg compression, the difference may not be immediately noticeable, but you can see that the character's armor and the rock in the distance look blurry. Let's zoom in on part of the image for a closer look:

The image on the left is rendered in 4K; the image on the right is 1080p stretched to 4K. The difference is much more noticeable in movement, because the softening of all the details quickly turns into a blurry mess. Part of the sharpness can be restored thanks to the sharpening effect of the graphics card drivers, but we wish we didn't have to do this at all.
This is where DLSS comes into play - in the first versionthis technology Nvidia analyzed several selected games; they ran in high resolutions, low resolutions, with and without anti-aliasing. In all of these modes, a set of images was generated and then loaded into the company's supercomputers, which used a neural network to determine how best to turn a 1080p image into an ideal, higher-resolution image.

I must say that DLSS 1.0 was not perfect : details were often lost and strange flickering appeared in some places. In addition, it did not use the graphics card's tensor cores themselves (it ran on the Nvidia network) and each DLSS-enabled game required a separate Nvidia research to generate the upscaling algorithm.

When version 2.0 was released in early 2020, major improvements were made to it. Most importantly, Nvidia's supercomputers were now only used to create a general upscaling algorithm - the new version of DLSS uses data from a rendered frame to process pixels using a neural model (GPU tensor cores).

We are impressed by the capabilities of DLSS 2.0 , but so far very few games support it - at the time of this writing, there were only 12. More and more developers want to implement it in their future games, and for good reason.
Any increase in scale can achieve significant productivity gains, so you can be confident that DLSS will continue to evolve.
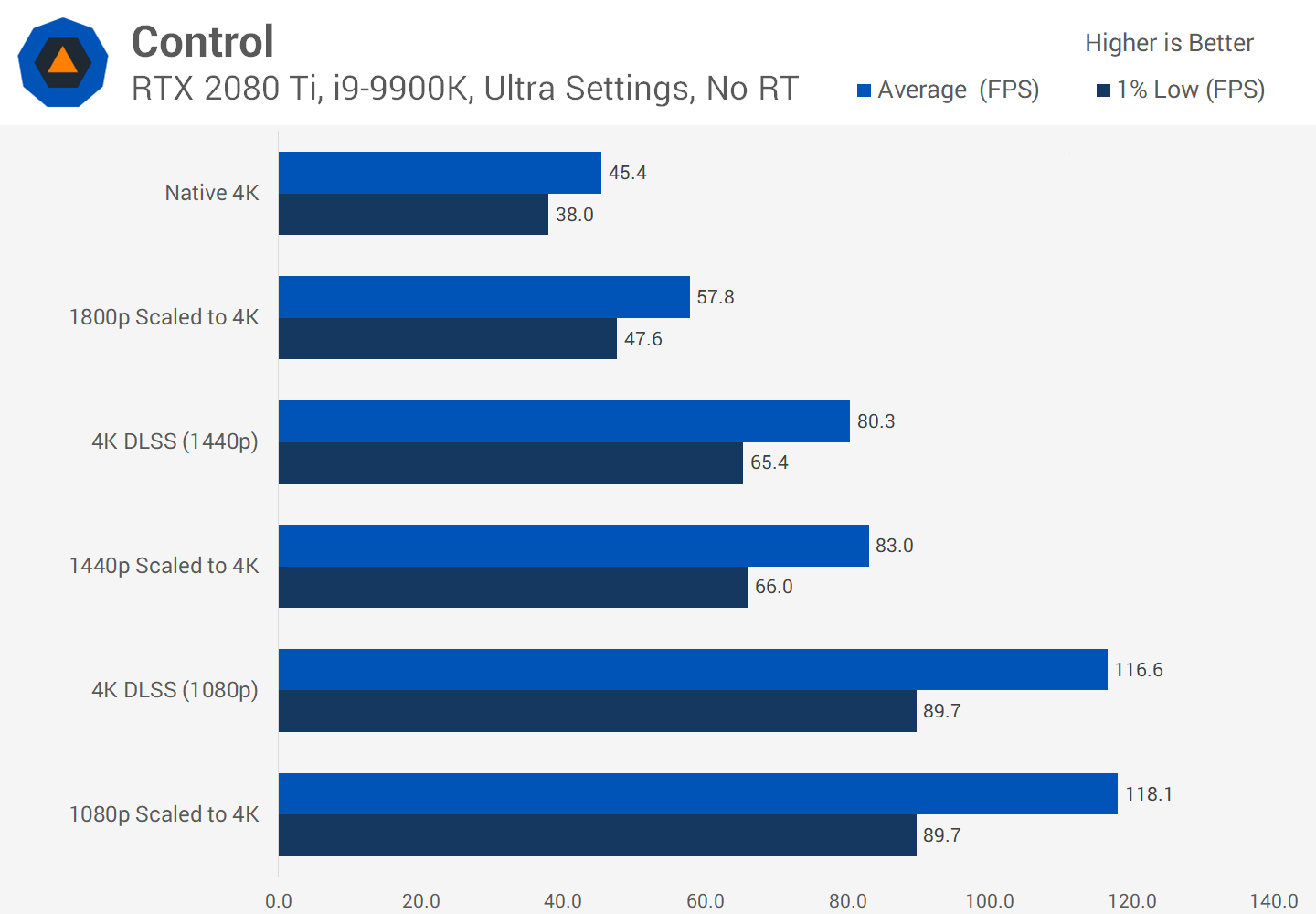
While the visual results of DLSS are not always perfect, by freeing up rendering resources, developers can add more visual effects or provide one level of graphics across a wider range of platforms.
For example, DLSS is often advertised along with ray tracing in "RTX-enabled" games. GeForce RTX cards contain additional computational blocks called RT cores, which are specialized logic blocks for speeding up ray-triangle intersection and traversal of the bounding volume hierarchy (BVH). These two processes are very time-consuming procedures that determine how light interacts with other objects in the scene.
As we found out, ray tracingIs a very time consuming process, so to ensure an acceptable level of frame rate in games, developers must limit the number of rays and reflections performed in the scene. This process can create grainy images, so a noise reduction algorithm must be applied, which increases processing complexity. It is expected that tensor kernels will improve the performance of this process by eliminating noise using AI, but this has yet to be realized: most modern applications still use CUDA kernels for this task. On the other hand, since DLSS 2.0 is becoming a very practical upsizing technique, Tensor Kernels can be effectively used to boost frame rates after ray tracing in a scene.
There are other plans to leverage the Tensor Cores of GeForce RTX cards, such as improving character animations or tissue simulation . But as with DLSS 1.0, it will be a long time before there are hundreds of games that use specialized matrix computing on the GPU.
A promising start
So, the situation is like this - tensor cores, excellent hardware units, which, however, are found only in some consumer-grade cards. Will anything change in the future? Since Nvidia has already significantly improved the performance of each Tensor Core in its Ampere architecture, there is a good chance that they will be installed in the lower- to mid-range model as well.
Although such cores are not yet in the GPUs of AMD and Intel, perhaps we will see them in the future. AMD has a system for sharpening or enhancing details in finished frames at the cost of a slight decrease in performance, so the company may stick to this system, especially since it does not need to be integrated by developers, it is enough to enable it in the drivers.
There is also a perception that the space on the crystals in graphics chips would be better spent on additional shader cores - this is what Nvidia did when creating budget versions of its Turing chips. In products such as the GeForce GTX 1650 , the company has completely ditched tensor cores and replaced them with additional FP16 shaders.
But for now, if you want to provide ultra-fast GEMM processing and take full advantage of it, then you have two options: buy a bunch of huge multicore CPUs or just one GPU with tensor cores.
See also: