Introduction
This article describes a stable non-recursive adaptive merge sort called quadsort.
Quadruple exchange
Quadsort is based on a quadruple exchange. Traditionally, most sorting algorithms are based on binary exchange, where two variables are sorted using a third temporary variable. It usually looks like this:
if (val[0] > val[1])
{
tmp[0] = val[0];
val[0] = val[1];
val[1] = tmp[0];
}In a quadruple exchange, sorting occurs using four substitution variables (swap). In the first step, the four variables are partially sorted into four swap variables, in the second step, they are completely sorted back into the four original variables.
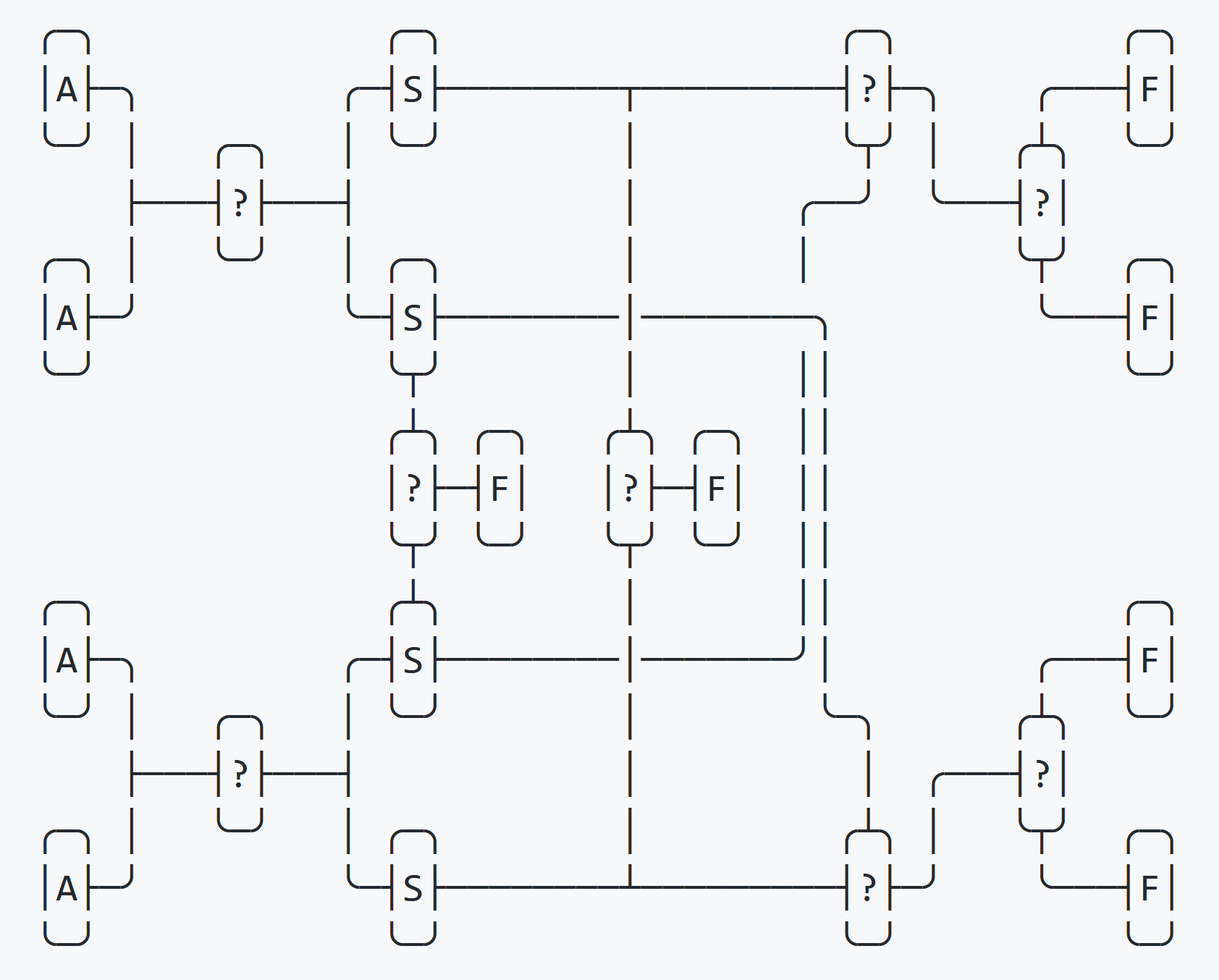
This process is shown in the diagram above.
After the first round of sorting, one if check determines if the four swap variables are sorted in order. If so, the exchange ends immediately. It then checks to see if the swap variables are sorted in reverse order. If so, the sort ends immediately. If both tests fail, then the final location is known and two tests remain to determine the final order.
This eliminates one unnecessary comparison for sequences that are in order. At the same time, one additional comparison is created for random sequences. However, in the real world, we rarely compare truly random data. So when the data is ordered rather than messy, this shift in probability is beneficial.
There is also an overall performance improvement due to the elimination of wasteful swap. In C, a basic quadruple swap looks like this:
if (val[0] > val[1])
{
tmp[0] = val[1];
tmp[1] = val[0];
}
else
{
tmp[0] = val[0];
tmp[1] = val[1];
}
if (val[2] > val[3])
{
tmp[2] = val[3];
tmp[3] = val[2];
}
else
{
tmp[2] = val[2];
tmp[3] = val[3];
}
if (tmp[1] <= tmp[2])
{
val[0] = tmp[0];
val[1] = tmp[1];
val[2] = tmp[2];
val[3] = tmp[3];
}
else if (tmp[0] > tmp[3])
{
val[0] = tmp[2];
val[1] = tmp[3];
val[2] = tmp[0];
val[3] = tmp[1];
}
else
{
if (tmp[0] <= tmp[2])
{
val[0] = tmp[0];
val[1] = tmp[2];
}
else
{
val[0] = tmp[2];
val[1] = tmp[0];
}
if (tmp[1] <= tmp[3])
{
val[2] = tmp[1];
val[3] = tmp[3];
}
else
{
val[2] = tmp[3];
val[3] = tmp[1];
}
}In case the array cannot be perfectly divided into four parts, the tail of 1-3 elements is sorted using the traditional binary exchange.
The quadruple exchange described above is implemented in quadsort.
Quadruple merge
At the first stage, the quadruple exchange pre-sorts the array into four-element blocks, as described above.
The second stage uses a similar approach for detecting ordered and reversed orders, but in blocks of 4, 16, 64, or more elements, this stage is treated like a traditional merge sort.
This can be represented as follows:
main memory: AAAA BBBB CCCC DDDD
swap memory: ABABABAB CDCDCDCD
main memory: ABCDABCDABCDABCDThe first line uses a quadruple swap to create four blocks of four sorted elements each. The second line uses a quad merge to combine into two blocks of eight sorted items each in swap memory. In the last line, the blocks are merged back into main memory, and we are left with one block of 16 sorted elements. Below is the visualization.

These operations actually require doubling the swap memory. More on this later.
Skip
Another difference is that due to the increased cost of merge operations, it is beneficial to check if four blocks are in forward or reverse order.
In case the four blocks are in order, the merge operation is skipped, since it is meaningless. However, this requires an additional if check, and for randomly sorted data, this if check becomes increasingly unlikely as the block size increases. Fortunately, the frequency of this if check is quadrupled each cycle, while the potential benefit quadruples each cycle.
In case the four blocks are in reverse order, a stable in-place swap is performed.
In the event that only two of the four blocks are ordered or are in reverse order, comparisons in the merge itself are unnecessary and are subsequently omitted. The data still needs to be copied into swap memory, but this is a less computational procedure.
This allows the quadsort algorithm to sort sequences in forward and backward order using
ncomparisons instead of n * log ncomparisons.
Boundary checks
Another problem with traditional merge sort is that it wastes resources on unnecessary boundary checks. It looks like this:
while (a <= a_max && b <= b_max)
if (a <= b)
[insert a++]
else
[insert b++]For optimization, our algorithm compares the last element of sequence A with the last element of sequence B. If the last element of sequence A is less than the last element of sequence B, then we know that the test
b < b_maxwill always be false, because sequence A is the first to completely merge.
Likewise, if the last element of sequence A is greater than the last element of sequence B, we know that the test
a < a_maxwill always be false. It looks like this:
if (val[a_max] <= val[b_max])
while (a <= a_max)
{
while (a > b)
[insert b++]
[insert a++]
}
else
while (b <= b_max)
{
while (a <= b)
[insert a++]
[insert b++]
}Fusion tail
When you sort a 65 element array, you end up with a 64 element sorted array and a one element sorted array at the end. This will not result in an additional swap (exchange) operation if the whole sequence is in order. In any case, for this, the program must choose the optimal array size (64, 256 or 1024).
Another problem is that the sub-optimal size of the array leads to unnecessary exchange operations. To work around these two problems, the quadruple merge procedure is aborted when the block size reaches 1/8 of the array size and the rest of the array is sorted using tail merge. The main advantage of tail fusion is that it allows the quadsort swap to be reduced to n / 2 without significantly impacting performance.
Big O
| Name | Best | Middle | Worst | Stable | Memory |
|---|---|---|---|---|---|
| quadsort | n | n log n | n log n | Yes | n |
When the data is already sorted or sorted in reverse order, quadsort makes n comparisons.
Cache
Since quadsort uses n / 2 swaps, cache usage is not as ideal as in-place sort. However, sorting the random data in place results in sub-optimal exchanges. Based on my benchmarks, quadsort is always faster than in-place sort, as long as the array does not overflow the L1 cache, which can be as high as 64KB on modern processors.
Wolfsort
Wolfsort is a hybrid radixsort / quadsort sorting algorithm that improves performance when working with random data. This is basically a proof of concept that only works with unsigned 32 and 64 bit integers.
Visualization
The visualization below runs four tests. The first test is based on a random distribution, the second on an ascending distribution, the third on a descending distribution, and the fourth on an ascending distribution with a random tail.
The top half shows swap and the bottom half shows main memory. Colors vary for skip, swap, merge and copy operations.
Benchmark: quadsort, std :: stable_sort, timsort, pdqsort and wolfsort
The following benchmark was run on WSL gcc configuration version 7.4.0 (Ubuntu 7.4.0-1ubuntu1 ~ 18.04.1). The source code is compiled by the team
g++ -O3 quadsort.cpp. Each test is run a hundred times and only the best run is reported.
The abscissa is the execution time.
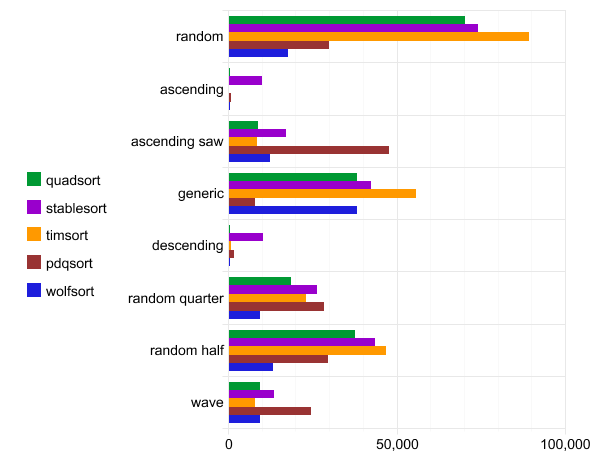
Quadsort datasheet, std :: stable_sort, timsort, pdqsort and wolfsort
| quadsort | 1000000 | i32 | 0.070469 | 0.070635 | ||
| stablesort | 1000000 | i32 | 0.073865 | 0.074078 | ||
| timsort | 1000000 | i32 | 0.089192 | 0.089301 | ||
| pdqsort | 1000000 | i32 | 0.029911 | 0.029948 | ||
| wolfsort | 1000000 | i32 | 0.017359 | 0.017744 | ||
| quadsort | 1000000 | i32 | 0.000485 | 0.000511 | ||
| stablesort | 1000000 | i32 | 0.010188 | 0.010261 | ||
| timsort | 1000000 | i32 | 0.000331 | 0.000342 | ||
| pdqsort | 1000000 | i32 | 0.000863 | 0.000875 | ||
| wolfsort | 1000000 | i32 | 0.000539 | 0.000579 | ||
| quadsort | 1000000 | i32 | 0.008901 | 0.008934 | () | |
| stablesort | 1000000 | i32 | 0.017093 | 0.017275 | () | |
| timsort | 1000000 | i32 | 0.008615 | 0.008674 | () | |
| pdqsort | 1000000 | i32 | 0.047785 | 0.047921 | () | |
| wolfsort | 1000000 | i32 | 0.012490 | 0.012554 | () | |
| quadsort | 1000000 | i32 | 0.038260 | 0.038343 | ||
| stablesort | 1000000 | i32 | 0.042292 | 0.042388 | ||
| timsort | 1000000 | i32 | 0.055855 | 0.055967 | ||
| pdqsort | 1000000 | i32 | 0.008093 | 0.008168 | ||
| wolfsort | 1000000 | i32 | 0.038320 | 0.038417 | ||
| quadsort | 1000000 | i32 | 0.000559 | 0.000576 | ||
| stablesort | 1000000 | i32 | 0.010343 | 0.010438 | ||
| timsort | 1000000 | i32 | 0.000891 | 0.000900 | ||
| pdqsort | 1000000 | i32 | 0.001882 | 0.001897 | ||
| wolfsort | 1000000 | i32 | 0.000604 | 0.000625 | ||
| quadsort | 1000000 | i32 | 0.006174 | 0.006245 | ||
| stablesort | 1000000 | i32 | 0.014679 | 0.014767 | ||
| timsort | 1000000 | i32 | 0.006419 | 0.006468 | ||
| pdqsort | 1000000 | i32 | 0.016603 | 0.016629 | ||
| wolfsort | 1000000 | i32 | 0.006264 | 0.006329 | ||
| quadsort | 1000000 | i32 | 0.018675 | 0.018729 | ||
| stablesort | 1000000 | i32 | 0.026384 | 0.026508 | ||
| timsort | 1000000 | i32 | 0.023226 | 0.023395 | ||
| pdqsort | 1000000 | i32 | 0.028599 | 0.028674 | ||
| wolfsort | 1000000 | i32 | 0.009517 | 0.009631 | ||
| quadsort | 1000000 | i32 | 0.037593 | 0.037679 | ||
| stablesort | 1000000 | i32 | 0.043755 | 0.043899 | ||
| timsort | 1000000 | i32 | 0.047008 | 0.047112 | ||
| pdqsort | 1000000 | i32 | 0.029800 | 0.029847 | ||
| wolfsort | 1000000 | i32 | 0.013238 | 0.013355 | ||
| quadsort | 1000000 | i32 | 0.009605 | 0.009673 | ||
| stablesort | 1000000 | i32 | 0.013667 | 0.013785 | ||
| timsort | 1000000 | i32 | 0.007994 | 0.008138 | ||
| pdqsort | 1000000 | i32 | 0.024683 | 0.024727 | ||
| wolfsort | 1000000 | i32 | 0.009642 | 0.009709 |
It should be noted that pdqsort is not a stable sort, so it works faster with data in normal order (general order).
The following benchmark was run on WSL gcc version 7.4.0 (Ubuntu 7.4.0-1ubuntu1 ~ 18.04.1). The source code is compiled by the team
g++ -O3 quadsort.cpp. Each test is run a hundred times and only the best run is reported. It measures performance on arrays ranging from 675 to 100,000 elements.
The X-axis of the graph below is the cardinality, the Y-axis is the execution time.

Quadsort datasheet, std :: stable_sort, timsort, pdqsort and wolfsort
| quadsort | 100000 | i32 | 0.005800 | 0.005835 | ||
| stablesort | 100000 | i32 | 0.006092 | 0.006122 | ||
| timsort | 100000 | i32 | 0.007605 | 0.007656 | ||
| pdqsort | 100000 | i32 | 0.002648 | 0.002670 | ||
| wolfsort | 100000 | i32 | 0.001148 | 0.001168 | ||
| quadsort | 10000 | i32 | 0.004568 | 0.004593 | ||
| stablesort | 10000 | i32 | 0.004813 | 0.004923 | ||
| timsort | 10000 | i32 | 0.006326 | 0.006376 | ||
| pdqsort | 10000 | i32 | 0.002345 | 0.002373 | ||
| wolfsort | 10000 | i32 | 0.001256 | 0.001274 | ||
| quadsort | 5000 | i32 | 0.004076 | 0.004086 | ||
| stablesort | 5000 | i32 | 0.004394 | 0.004420 | ||
| timsort | 5000 | i32 | 0.005901 | 0.005938 | ||
| pdqsort | 5000 | i32 | 0.002093 | 0.002107 | ||
| wolfsort | 5000 | i32 | 0.000968 | 0.001086 | ||
| quadsort | 2500 | i32 | 0.003196 | 0.003303 | ||
| stablesort | 2500 | i32 | 0.003801 | 0.003942 | ||
| timsort | 2500 | i32 | 0.005296 | 0.005322 | ||
| pdqsort | 2500 | i32 | 0.001606 | 0.001661 | ||
| wolfsort | 2500 | i32 | 0.000509 | 0.000520 | ||
| quadsort | 1250 | i32 | 0.001767 | 0.001823 | ||
| stablesort | 1250 | i32 | 0.002812 | 0.002887 | ||
| timsort | 1250 | i32 | 0.003789 | 0.003865 | ||
| pdqsort | 1250 | i32 | 0.001036 | 0.001325 | ||
| wolfsort | 1250 | i32 | 0.000534 | 0.000655 | ||
| quadsort | 675 | i32 | 0.000368 | 0.000592 | ||
| stablesort | 675 | i32 | 0.000974 | 0.001160 | ||
| timsort | 675 | i32 | 0.000896 | 0.000948 | ||
| pdqsort | 675 | i32 | 0.000489 | 0.000531 | ||
| wolfsort | 675 | i32 | 0.000283 | 0.000308 |
Benchmark: quadsort and qsort (mergesort)
The next benchmark was run on WSL gcc version 7.4.0 (Ubuntu 7.4.0-1ubuntu1 ~ 18.04.1). The source code is compiled by the team
g++ -O3 quadsort.cpp. Each test is run a hundred times and only the best run is reported.
quadsort: sorted 1000000 i32s in 0.119437 seconds. MO: 19308657 ( )
qsort: sorted 1000000 i32s in 0.133077 seconds. MO: 21083741 ( )
quadsort: sorted 1000000 i32s in 0.002071 seconds. MO: 999999 ()
qsort: sorted 1000000 i32s in 0.007265 seconds. MO: 3000004 ()
quadsort: sorted 1000000 i32s in 0.019239 seconds. MO: 4007580 ( )
qsort: sorted 1000000 i32s in 0.071322 seconds. MO: 20665677 ( )
quadsort: sorted 1000000 i32s in 0.076605 seconds. MO: 19242642 ( )
qsort: sorted 1000000 i32s in 0.038389 seconds. MO: 6221917 ( )
quadsort: sorted 1000000 i32s in 0.002305 seconds. MO: 999999 ()
qsort: sorted 1000000 i32s in 0.009659 seconds. MO: 4000015 ()
quadsort: sorted 1000000 i32s in 0.022940 seconds. MO: 9519209 ( )
qsort: sorted 1000000 i32s in 0.042135 seconds. MO: 13152042 ( )
quadsort: sorted 1000000 i32s in 0.034456 seconds. MO: 6787656 ( )
qsort: sorted 1000000 i32s in 0.098691 seconds. MO: 20584424 ( )
quadsort: sorted 1000000 i32s in 0.066240 seconds. MO: 11383441 ( )
qsort: sorted 1000000 i32s in 0.118086 seconds. MO: 20572142 ( )
quadsort: sorted 1000000 i32s in 0.038116 seconds. MO: 15328606 ( )
qsort: sorted 1000000 i32s in 4.471858 seconds. MO: 1974047339 ( )
quadsort: sorted 1000000 i32s in 0.060989 seconds. MO: 15328606 ()
qsort: sorted 1000000 i32s in 0.043175 seconds. MO: 10333679 ()
quadsort: sorted 1023 i32s in 0.016126 seconds. (random 1-1023)
qsort: sorted 1023 i32s in 0.033132 seconds. (random 1-1023)MO indicates the number of comparisons performed on 1 million items.
The benchmark above compares quadsort to glibc qsort () through the same general purpose interface and without any known unfair advantages such as inlining.
random order: 635, 202, 47, 229, etc
ascending order: 1, 2, 3, 4, etc
uniform order: 1, 1, 1, 1, etc
descending order: 999, 998, 997, 996, etc
wave order: 100, 1, 102, 2, 103, 3, etc
stable/unstable: 100, 1, 102, 1, 103, 1, etc
random range: time to sort 1000 arrays ranging from size 0 to 999 containing random dataBenchmark: quadsort and qsort (quicksort)
This particular test is done using Cygwin's qsort () implementation, which uses quicksort under the hood. The source code is compiled by the team
gcc -O3 quadsort.c. Each test is executed a hundred times, only the best run is reported.
quadsort: sorted 1000000 i32s in 0.119437 seconds. MO: 19308657 ( )
qsort: sorted 1000000 i32s in 0.133077 seconds. MO: 21083741 ( )
quadsort: sorted 1000000 i32s in 0.002071 seconds. MO: 999999 ()
qsort: sorted 1000000 i32s in 0.007265 seconds. MO: 3000004 ()
quadsort: sorted 1000000 i32s in 0.019239 seconds. MO: 4007580 ( )
qsort: sorted 1000000 i32s in 0.071322 seconds. MO: 20665677 ( )
quadsort: sorted 1000000 i32s in 0.076605 seconds. MO: 19242642 ( )
qsort: sorted 1000000 i32s in 0.038389 seconds. MO: 6221917 ( )
quadsort: sorted 1000000 i32s in 0.002305 seconds. MO: 999999 ()
qsort: sorted 1000000 i32s in 0.009659 seconds. MO: 4000015 ()
quadsort: sorted 1000000 i32s in 0.022940 seconds. MO: 9519209 ( )
qsort: sorted 1000000 i32s in 0.042135 seconds. MO: 13152042 ( )
quadsort: sorted 1000000 i32s in 0.034456 seconds. MO: 6787656 ( )
qsort: sorted 1000000 i32s in 0.098691 seconds. MO: 20584424 ( )
quadsort: sorted 1000000 i32s in 0.066240 seconds. MO: 11383441 ( )
qsort: sorted 1000000 i32s in 0.118086 seconds. MO: 20572142 ( )
quadsort: sorted 1000000 i32s in 0.038116 seconds. MO: 15328606 ( )
qsort: sorted 1000000 i32s in 4.471858 seconds. MO: 1974047339 ( )
quadsort: sorted 1000000 i32s in 0.060989 seconds. MO: 15328606 ()
qsort: sorted 1000000 i32s in 0.043175 seconds. MO: 10333679 ()
quadsort: sorted 1023 i32s in 0.016126 seconds. (random 1-1023)
qsort: sorted 1023 i32s in 0.033132 seconds. (random 1-1023)In this benchmark, it becomes clear why quicksort is often preferable to traditional merge, it does fewer comparisons for data in ascending order, uniformly distributed, and for data in descending order. However, in most tests it performed worse than quadsort. Quicksort also exhibits an extremely slow sorting speed for wave-ordered data. The random data test shows that quadsort is more than twice as fast when sorting small arrays.
Quicksort is faster on general purpose and stable tests, but only because it is an unstable algorithm.
See also: