What is music in terms of mathematics? What is "la" or "mi"? How exactly sounds are formed is well understood on the guitar.
Sound "mi" (free sound of the 1st string), sound "la" ( 1st string clamped at the 5th fret ). "La" is 440 Hz. What does 440 Hz mean? That's 440 times the string vibrates per second. The "mi" sound is 5 semitones lower than the "la" sound ( clamped at the 5th fret ).

Another 7 semitones lower, I will get "mi" again, i.e. octave. Why are both the free sounding of the first string and the sounding of the string clamped at the 12th fret called the same word "mi"?

It seems to us that the same note is being played. The fact is that the length of the string by this point ( "mi" at the 12th fret ) is divided exactly in half:
This means that the vibrations of this remainder of the string, according to the laws of physics, will be twice as frequent as the vibrations of a full string.
Each time I step back down the string and clamp it at the next fret (the division indicated by the perpendicular line on the fretboard ), the sound goes up one semitone, as the musicians say.
Note that the frets on the fretboard are of different widths. They gradually taper, because in order to raise the frequency by one semitone, you need to reduce the string length by a certain number of times.
What am I hinting at by focusing on the fact that something "on" is translated into something "in"? Mathematicians would say that there is only one (under certain conditions) function where + goes to x ( multiply ). And this function is called the logarithm.
This means that our ears, shortening the strings and raising the sound a certain number of times, perceive it as raising one semitone. That is, each fret shortens the string by the same number of times, and our ears say that we go up one semitone, reaching the note "E" and receiving an octave. Our hearing organs are logarithmic.
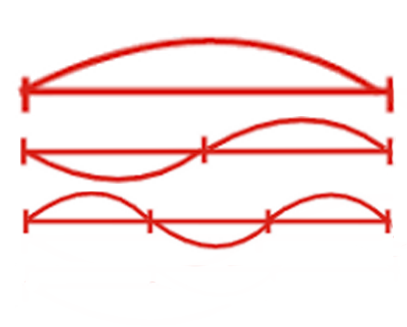
We say that "mi" and "mi" are two times different, this can be seen from the sound. The upper arc is full swing. When we clamp it in the middle, the string begins to vibrate, as in the graph in the middle.
Why are the sounds similar? The fact is that along with the main vibration of the string, in fact, the vibration of the same string occurs at all frequencies, where the length of the vibrational section is inversely proportional to the frequency.
Accordingly, if the length decreases by an integer number of times, then the corresponding overtone can be heard. The corresponding overtone is realized by the given string. If a given string vibrates partially fixed at these two points ( bottom graph ), then its tone will be three times higher.
A double increase in frequency is perceived by the ear as the same note. All overtones that we divide several times, i.e. any division of a half segment is both automatic division and a large segment. And only some divisions of a large segment do not fit into the half division scheme.
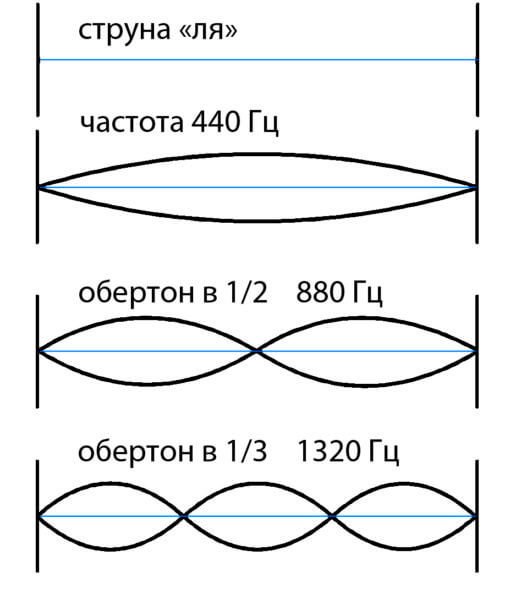
If we take the even-numbered upper tones for a long string, then they will be the upper tones for a half-shortened string. And absolutely any shortened sound of a short string will sound for a long one. Therefore, we feel that everything we hear coincides at these points, and we perceive it as one note.
It is even more interesting that there are notes that go through several semitones, and they are perceived by our ears as a consonance, a chord, something pleasing to the ear, not cutting our ears. What are these notes?
If you take 7 semitones, take the note "A" and raise the sound by 7 semitones, until the next "E", then those two notes will sound good.
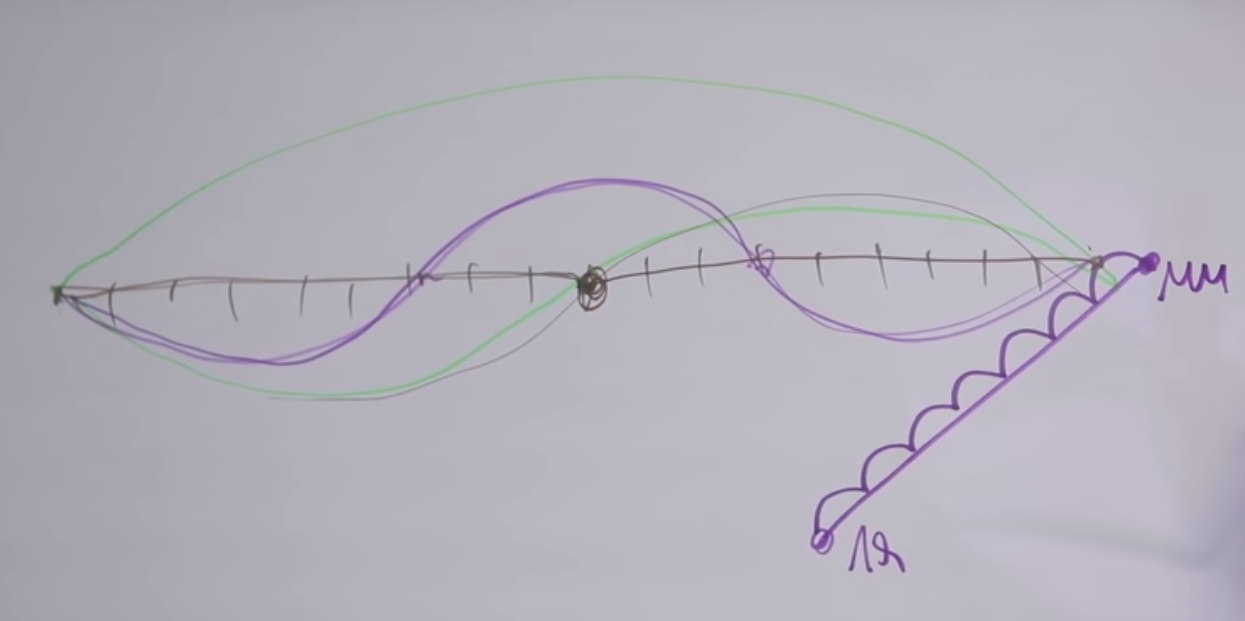
If you step back another 5 semitones up, then there will be a higher "la" of the next octave. For some reason, this interval also sounds pleasant to us. Let's figure it all out.
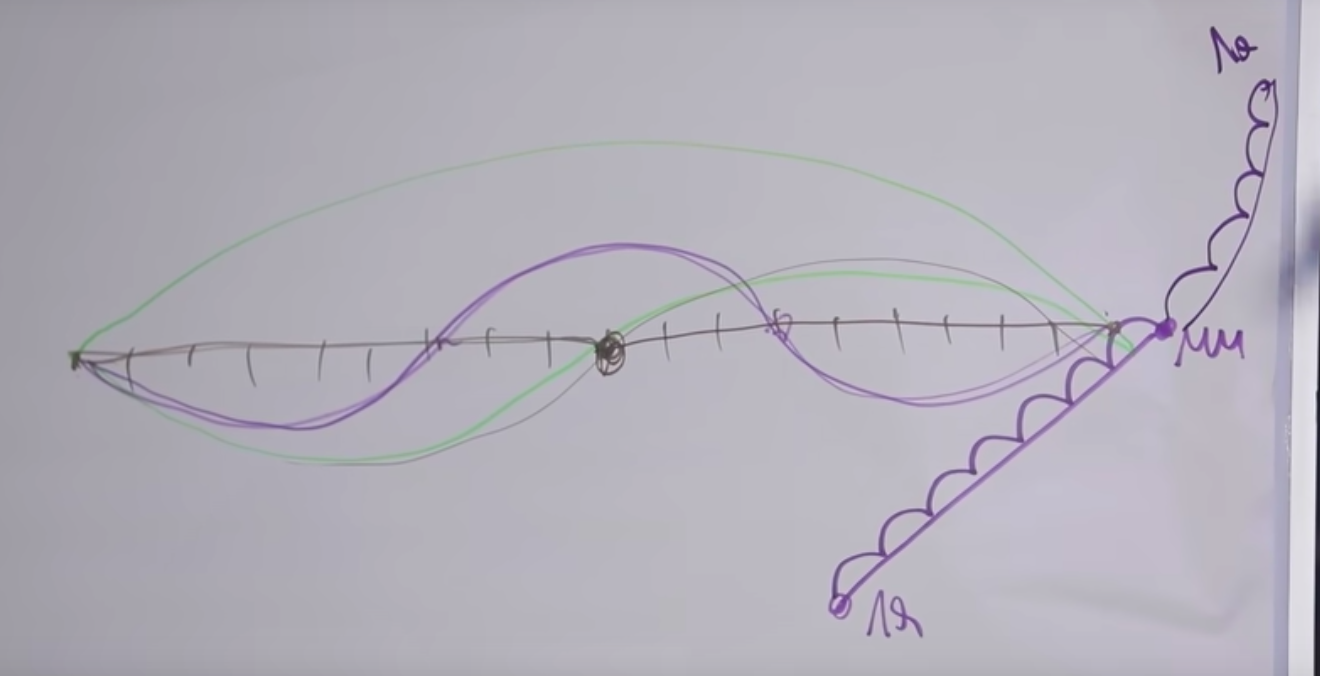
First of all, if an increase by 1 semitone is an increase in the frequency of oscillations by a certain number of times, then we will designate it as x. If you need to raise one more semitone, then there will already be x * x, that is, x 2 . If I raised it 12 semitones (x 12 ), then it should be raising exactly 2 times. We get the equation x 12 = 2.
Therefore, an increase of 1 semitone means a string contraction at x = 12√2, or, which is the same, raising the frequency of sound by 12 √2.
And what have "la" and "mi" to do with it? Why does 7 semitones sound melodic? Let's raise the degree:
What is so pleasant, good in this number?
Sometime in antiquity, tempered claviers, an accurate recording of music, were invented. You can see it very well on the guitar, you can also find it on the piano, it is hidden inside, if you look, you can see the strings.
Now, this number is very close to 3/2. If you calculate on a calculator, it will be very accurate. This means that "mi" is approximately 1.5 times higher than the previous "la". Those. lifting 7 tones is equivalent to going up 3/2 times, which means that we have a lot of upper overtones coinciding.
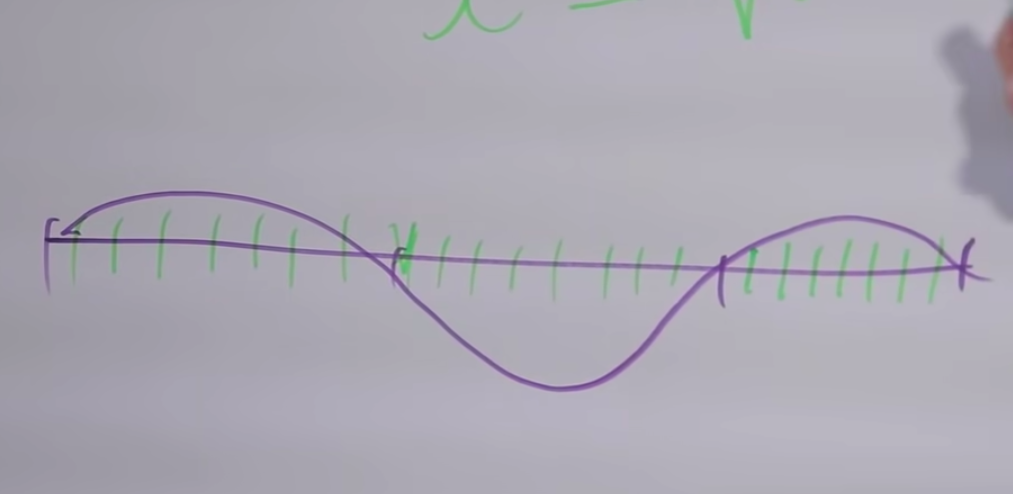
Because any division by an integer of a small segment will be an integer division of the entire segment. And, accordingly, dividing the original cut by the number of pieces, a multiple of three, will be the division of the small segment (⅓), and ⅔ too. When we left ⅔ from the length, i.e. raised the frequency to 3/2, we went up about 7 semitones, we will have many common overtones, it will be a pleasant consonance.
The remaining 4/3 is exactly the 5 remaining semitones, 3/2 x 4/3 = 2, just an octave. Which corresponds to the formula x71243. The value is very close to 4/3, but not 100%. This number is irrational, cannot be written as a fraction, it cannot be written as an integer divided by an integer.
I heard that there is an instrument in India ( sitar), in which the octave is divided into 19 parts, i.e. they have a semitone = 1/19 octave, 19x2.

And already with great accuracy x121932, which means if on such an Indian instrument you step back 12 out of 19 segments, then in this consonance there will be more coinciding overtones, and this interval sounds like a balm for the ears.
There are many interesting things to say about music and mathematics. In particular, a major chord is perceived if 4 semitones are added to any initial note, and then 3, i.e. 0 - 4 - 3. A minor, if at the beginning add 3, and then 4, i.e. 0 - 3 - 4. The first and last of the three notes of the chord will be "the same", it just differs by 7 semitones, but the middle sound will create our perception of consonance, and tune in a minor or major mode.
It would seem that music and mathematics, what can be in common? And there is so much in common that mathematicians and musicians often communicate, moreover, mathematicians easily understand musicians, so to speak, they grasp a semitone.
Several useful links:
- Music theory for geeks
- Notation is not taught correctly *
- Why is there so much mathematics in music?