
Who am I
My name is Dmitry Ivanov. I am a 2nd year graduate student in economics at the St. Petersburg HSE. I work in the research group " Agent Systems and Reinforcement Learning " at JetBrains Research , as well as in the International Laboratory of Game Theory and Decision Making at the Higher School of Economics . In addition to PU learning, I am interested in reinforcement learning and research at the intersection of machine learning and economics.
Preamble
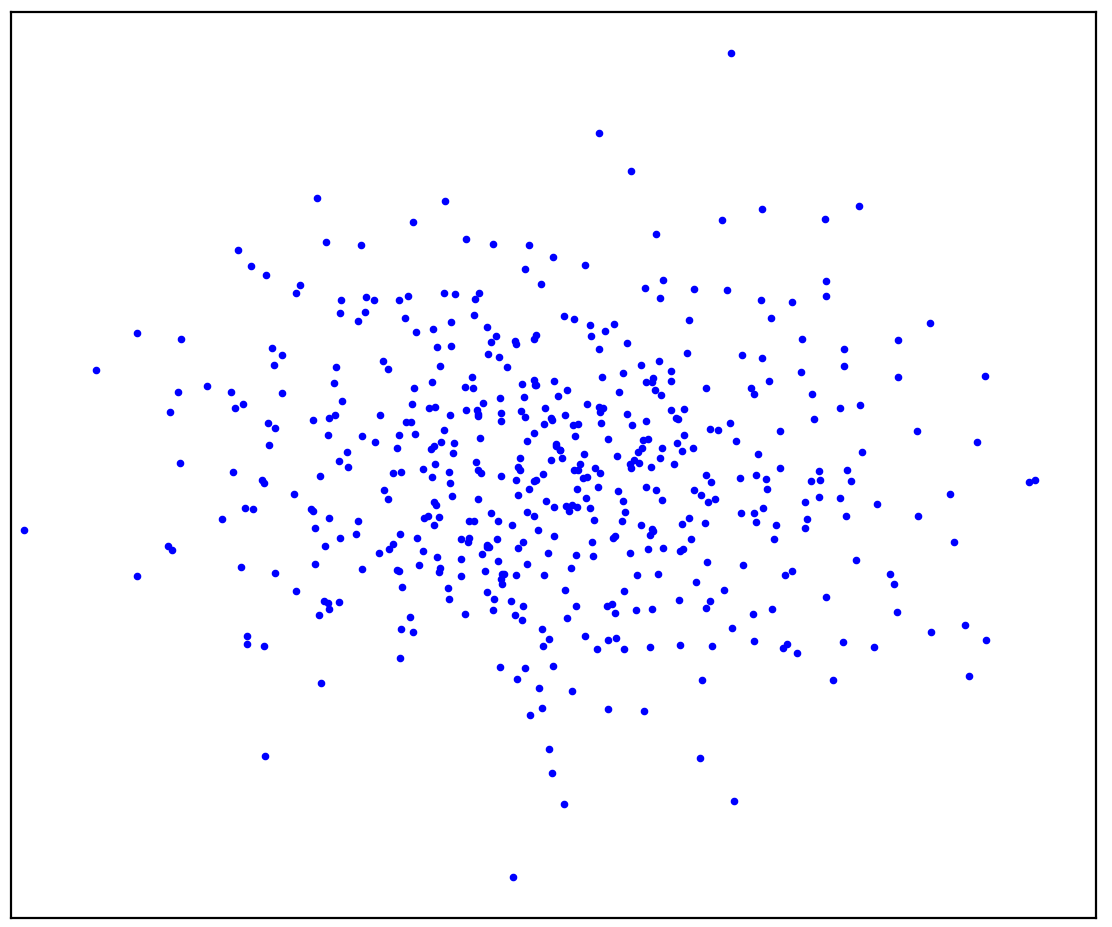
Figure: 1a. Positive data
Figure 1a shows a set of points generated by some distribution, which we will call positive. All other possible points that do not belong to the positive distribution will be called negative. Try to mentally draw a line separating the positive points presented from all possible negative points. By the way, this task is called "anomaly detection".
The answer is here

. 1.

. 1.
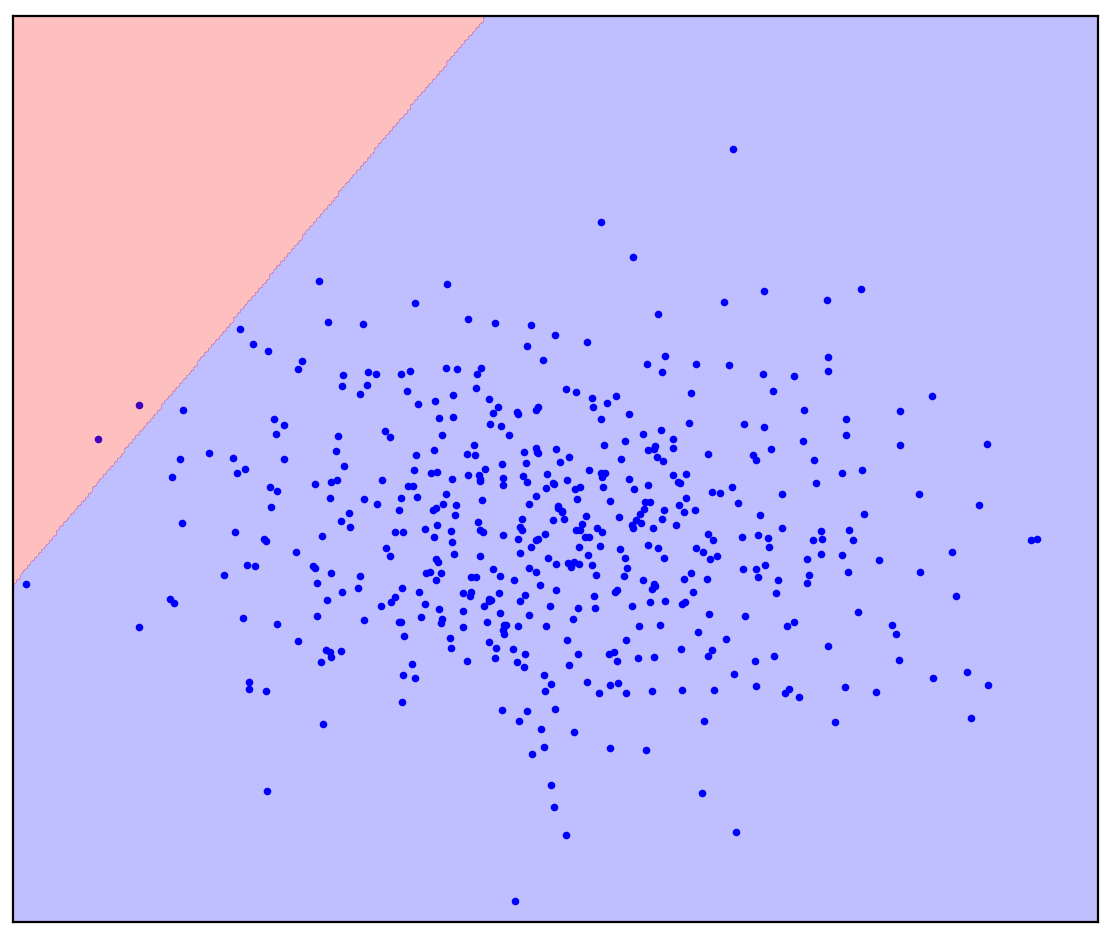
You may have imagined something like Figure 1b: circled the data in an ellipse. In fact, this is how many anomaly detection methods work.
Now let's change the problem a little: let us have additional information that a straight line should separate positive points from negative ones. Try to draw it in your mind.
The answer is here
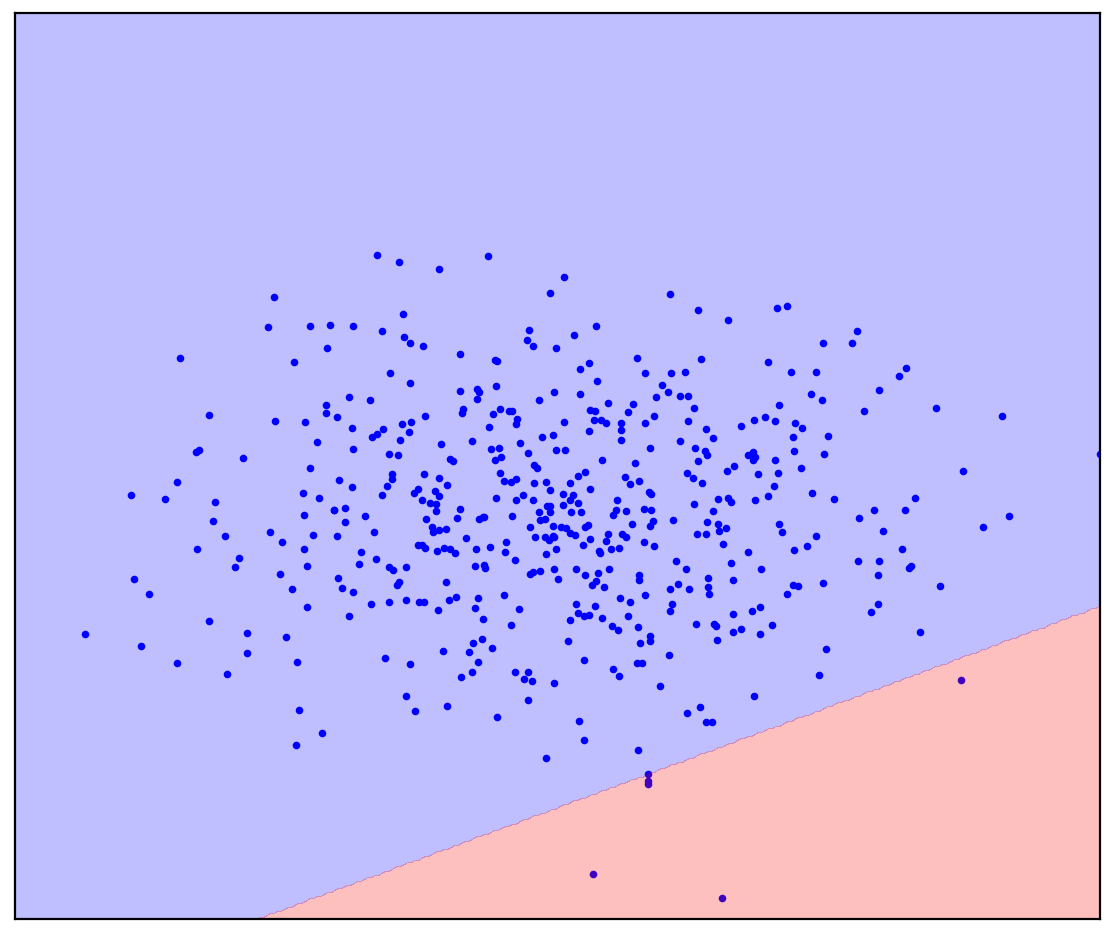
. 1. ( One-Class SVM)



. 1. ( One-Class SVM)
In the case of a straight dividing line, there is no single answer. It is not clear in which direction to draw a straight line.
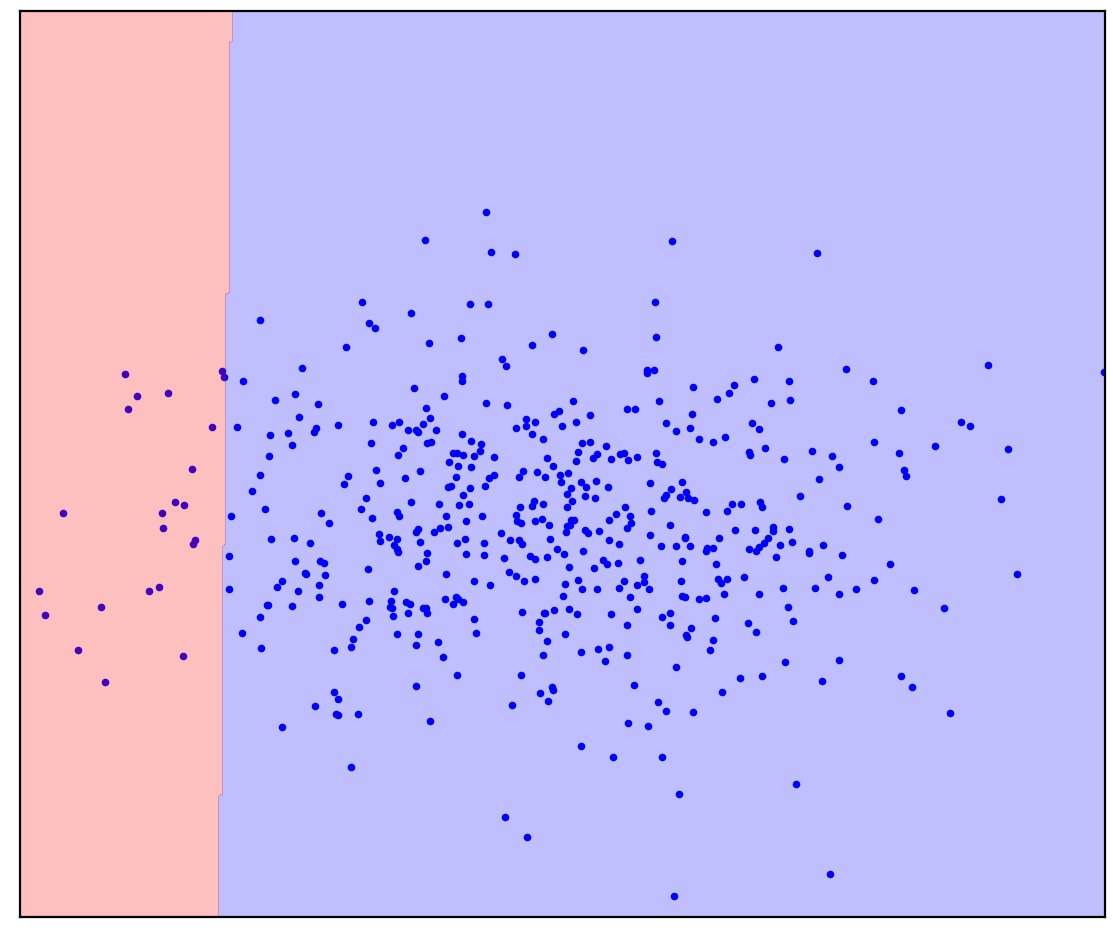
Now I will add some unallocated points to Figure 1d that contain a mixture of positive and negative. For the last time, I will ask you to make a mental effort and imagine a line separating the positive and negative points. But this time, you can use unlabeled data!

Figure: 1d. Positive (blue) and unlabeled (red) points. Unmarked points are composed of positive and negative
The answer is here

. 1.

. 1.
It became easier! Although we do not know in advance how each particular unmarked point is generated, we can roughly mark them by comparing them with positive ones. Red dots that look like blue are probably positive. On the contrary, dissimilar ones are probably negative. As a result, despite the fact that we do not have “clean” negative data, information about them can be obtained from the unlabeled mixture and used for a more accurate classification. This is what the Positive-Unlabeled learning algorithms, which I want to talk about, do.
Introduction
Positive-Unlabeled (PU) learning can be translated as "learning from positive and unlabeled data." In fact, PU learning is an analogue of a binary classification for cases when there is labeled data of only one of the classes, but an unlabeled mixture of data from both classes is available. In the general case, we do not even know how much data in the mixture corresponds to a positive class and how much to a negative one. Based on such datasets, we want to build a binary classifier: the same as in the presence of pure data of both classes.
As a toy example, consider a classifier for pictures of cats and dogs. We have some pictures of cats and many more pictures of both cats and dogs. At the output, we want to get a classifier: a function that predicts for each picture the probability that a cat is depicted. At the same time, the classifier can mark our existing mixture of pictures for cats and dogs. At the same time, it can be difficult / expensive / time-consuming / impossible to manually mark up pictures for training the classifier, you want to do it without it.
PU learning is a fairly natural task. Data found in the real world is often dirty. The ability to learn from dirty data seems to be a useful life hack with relatively high quality. Despite this, I have met paradoxically few people who have heard about PU learning, and even fewer who would have known about any specific methods. So I decided to talk about this area.

Figure: 2. Jürgen Schmidhuber and Yann LeCun, NeurIPS 2020
Application of PU learning
I will informally divide the cases in which PU learning can be useful into three categories.
The first category is probably the most obvious: PU learning can be used instead of the usual binary classification. In some tasks, the data is inherently slightly dirty. In principle, this contamination can be ignored and a conventional classifier can be used. However, it is possible to change very little the loss function when training the classifier (Kiryo et al., 2017) or even the predictions themselves after training (Elkan & Noto, 2008) , and the classification becomes more accurate.
As an example, consider the identification of new genes responsible for the development of disease genes. The standard approach is to treat the disease genes already found as positive and all other genes as negative. Obviously, this negative data may contain disease genes not yet found. Moreover, the task itself is to search for such disease genes among the "negative" data. This internal contradiction is noticed here: (Yang et al., 2012) . The researchers deviated from the standard approach and considered genes not related to already discovered disease genes as an unlabeled mixture, and then applied PU learning methods.
Another example is reinforcement learning based on expert demonstrations. The challenge is to train the agent to act in the same way as an expert. This can be achieved using the generative adversarial imitation learning (GAIL) method. GAIL uses a GAN-like (generative adversarial networks) architecture: the agent generates trajectories so that the discriminator (classifier) cannot distinguish them from the expert's demonstrations. Researchers from DeepMind recently noticed that in GAIL, the discriminator solves the PU learning problem (Xu & Denil, 2019)... Usually, the discriminator considers the expert data to be positive, and the generated data to be negative. This approximation is fairly accurate at the beginning of training when the generator is not capable of producing data that looks like positive. However, as the training progresses, the generated data looks more like expert data until it becomes indistinguishable to the discriminator at the end of the training. For this reason, researchers (Xu & Denil, 2019) consider the generated data to be unlabeled data with a variable mix ratio. Later, the GAN was modified in a similar way when generating images (Guo et al., 2020) .

Figure: 3. PU learning as an analogue of standard PN classification
In the second category, PU learning can be used for anomaly detection as an analogue of one-class classification (OCC). We have already seen in the Preamble how exactly untagged data can help. All OSS methods, without exception, are forced to make an assumption about the distribution of negative data. For example, it is wise to circle positive data into an ellipse (a hypersphere in the multidimensional case), outside of which all points are negative. In this case, we assume that the negative data is evenly distributed (Blanchard et al., 2010)... Rather than making such assumptions, PU learning methods can estimate the distribution of negative data based on unlabeled data. This is especially important if the distributions of the two classes overlap strongly (Scott & Blanchard, 2009) . One example of anomaly detection using PU learning is fake review detection (Ren et al., 2014) .

Figure: 4. An example of a fake review
Detection of corruption in Russian public procurement auctions
The third category of PU learning can be attributed to problems in which neither binary nor single-class classification can be used. As an example, I will tell you about our project to detect corruption in auctions of Russian public procurements (Ivanov & Nesterov, 2019) .
According to the legislation, complete data on all public procurement auctions are placed in the public domain for everyone who wants to spend a month parsing them. We have collected data from more than a million auctions held from 2014 to 2018. Who put, when and how much, who won, during what period the auction took place, who held, what purchased - all this is in the data. But, of course, there is no label “corruption is here”, so you cannot build an ordinary classifier. Instead, we applied PU learning. Basic assumption: Participants with an unfair advantage will always win. Using this assumption, the losers in the auctions can be considered as fair (positive), and the winners as potentially dishonest (untagged).In this setting, PU learning methods can find suspicious patterns in the data based on subtle differences between winners and losers. Of course, in practice, difficulties arise: an accurate design of features for the classifier, an analysis of the interpretability of its predictions, and statistical verification of assumptions about data are required.
According to our very conservative estimate, about 9% of auctions in the data are corrupt, as a result of which the state loses about 120 million rubles a year. The losses may not seem very large, but the auctions we study occupy only about 1% of the public procurement market.


Figure: 5. The share of corrupt public procurement auctions in different regions of Russia (Ivanov & Nesterov, 2019)
Concluding remarks
To avoid the impression that PU is the solution to all the troubles of mankind, I will mention the pitfalls. In a conventional classification, the more data we have, the more accurate the classifier can be. Moreover, by increasing the amount of data to infinity, we can approach the ideal (according to Bayesian formula) classifier. So, the main catch of PU learning is that it is an ill-posed problem, that is, a problem that cannot be solved unambiguously even with an infinite amount of data. The situation becomes better if the proportion of two classes in unlabeled data is known, however, determining this proportion is also an ill-posed problem (Jain et al., 2016)... The best we can define is the spacing the proportion is in. Moreover, PU learning methods often do not offer ways to estimate this proportion and consider it to be known. There are separate methods that estimate it (the task is called Mixture Proportion Estimation), but they are often slow and / or unstable, especially when the two classes are very unevenly represented in the mixture.
In this post, I talked about the intuitive definition and application of PU learning. In addition, I can talk about the formal definition of PU learning with formulas and their explanations, as well as about classical and modern PU learning methods. If this post arouses interest, I will write a sequel.
Bibliography
Blanchard, G., Lee, G., & Scott, C. (2010). Semi-supervised novelty detection. Journal of Machine Learning Research, 11(Nov), 2973–3009.
Elkan, C., & Noto, K. (2008). Learning classifiers from only positive and unlabeled data. Proceeding of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining — KDD 08, 213. https://doi.org/10.1145/1401890.1401920
Guo, T., Xu, C., Huang, J., Wang, Y., Shi, B., Xu, C., & Tao, D. (2020). On Positive-Unlabeled Classification in GAN. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8385–8393.
Ivanov, D. I., & Nesterov, A. S. (2019). Identifying Bid Leakage In Procurement Auctions: Machine Learning Approach. ArXiv Preprint ArXiv:1903.00261.
Jain, S., White, M., Trosset, M. W., & Radivojac, P. (2016). Nonparametric semi-supervised learning of class proportions. ArXiv Preprint ArXiv:1601.01944.
Kiryo, R., Niu, G., du Plessis, M. C., & Sugiyama, M. (2017). Positive-unlabeled learning with non-negative risk estimator. Advances in Neural Information Processing Systems, 1675–1685.
Ren, Y., Ji, D., & Zhang, H. (2014). Positive Unlabeled Learning for Deceptive Reviews Detection. EMNLP, 488–498.
Scott, C., & Blanchard, G. (2009). Novelty detection: Unlabeled data definitely help. Artificial Intelligence and Statistics, 464–471.
Xu, D., & Denil, M. (2019). Positive-Unlabeled Reward Learning. ArXiv:1911.00459 [Cs, Stat]. http://arxiv.org/abs/1911.00459
Yang, P., Li, X.-L., Mei, J.-P., Kwoh, C.-K., & Ng, S.-K. (2012). Positive-unlabeled learning for disease gene identification. Bioinformatics, 28(20), 2640–2647.