The challenge of how to safely reopen offices, schools and other public places while keeping people a meter and a half apart comes down to a question that mathematicians have been studying for centuries.

It may seem that such a topic as the packing of spheres will appeal only to mathematicians. Who else would be interested in looking for the most effective ways to place circles on a plane or spheres in space?
However, today millions of people around the world are pondering precisely this task.
Determining how to safely open buildings and public spaces while maintaining social distance is, in particular, an exercise in geometry. If each person must be at least one and a half meters away from other people, then to calculate how many people can sit in the classroom or dining room, you need to pack non-overlapping circles on the floor plan.

Naturally, to combat the coronavirus, many more problems need to be solved than this geometric one. However, the packing of circles and spheres plays a role in this - just like the modeling of crystal structures in chemistry and abstract message spaces in information theory. This task, seemingly simple in description, has occupied the minds of the greatest mathematicians in history, and the most interesting research in this area is being conducted today, in particular, in higher dimensions. For example, mathematicians recently found the best way to pack in 8- and 24-dimensional spaces - a technique needed to optimize error correction codes used both in cell phones and in communication with space probes. So let's take a look at some of the unexpected complications that arise when we try to fill a space with the simplest form.
Whether you're packing oranges in boxes at work or safely seating students with social distancing, the size and shape of your container is critical to your task. However, for most mathematicians, sphere packing theory is about filling the entire space. In two dimensions, this means covering the plane with disjoint circles of the same size.
Here is one example of packing circles on a plane. It looks like a top view of a soda package:

You can imagine how this pattern is repeated in all directions, like a tile that has been paved with a plane. Small gaps between circles indicate that the plane is not completely filled, but in the case of packing circles this should be expected. We are interested in what percentage of the plane is covered. This will be the "packing density" of the particular method.
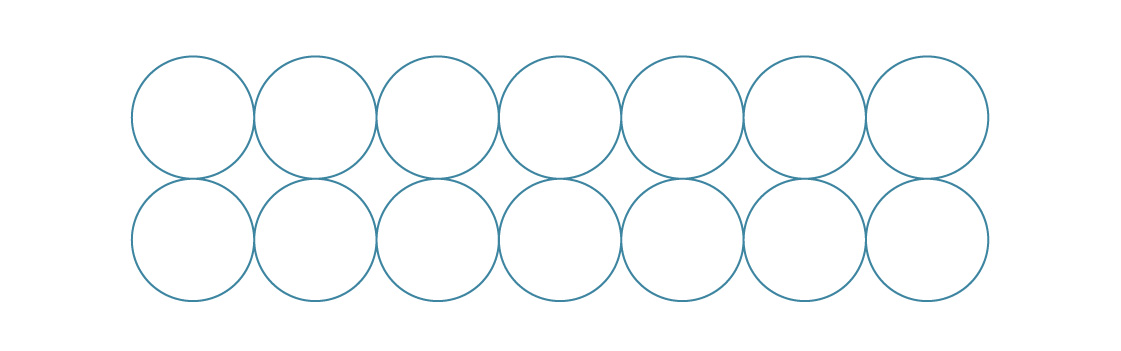
The above method is called square packing, and for good reason - the centers of the circles can be represented as the vertices of the squares.
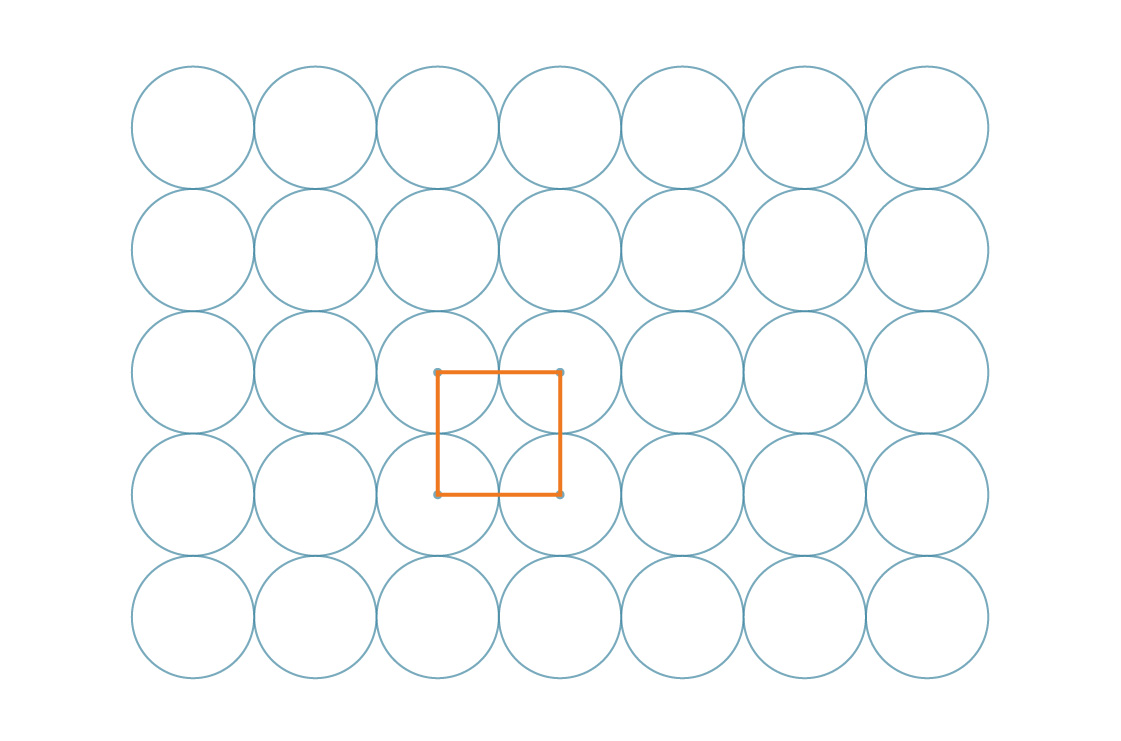
And in fact, these squares themselves tile the plane:
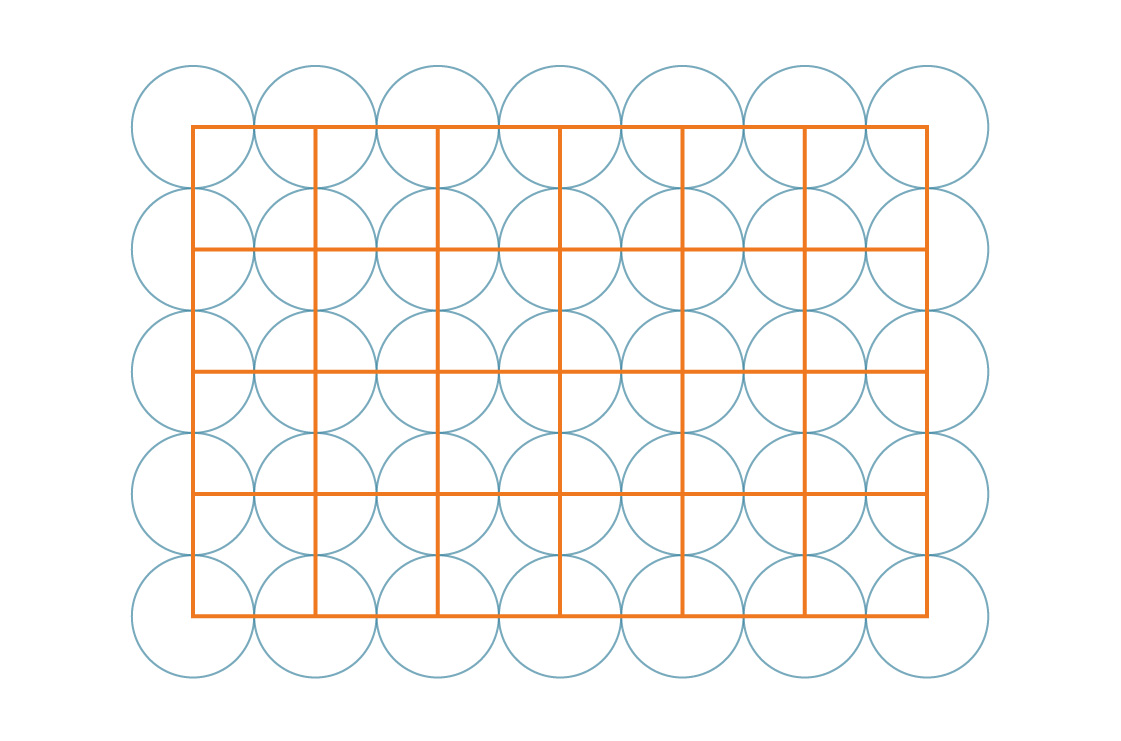
Our task is facilitated by the symmetry of the pattern. Since these squares cover the entire plane in a periodic manner, the percentage of the plane covered by the circles is the same as the percentage of the square covered by the circles. Let's look at one of these squares.
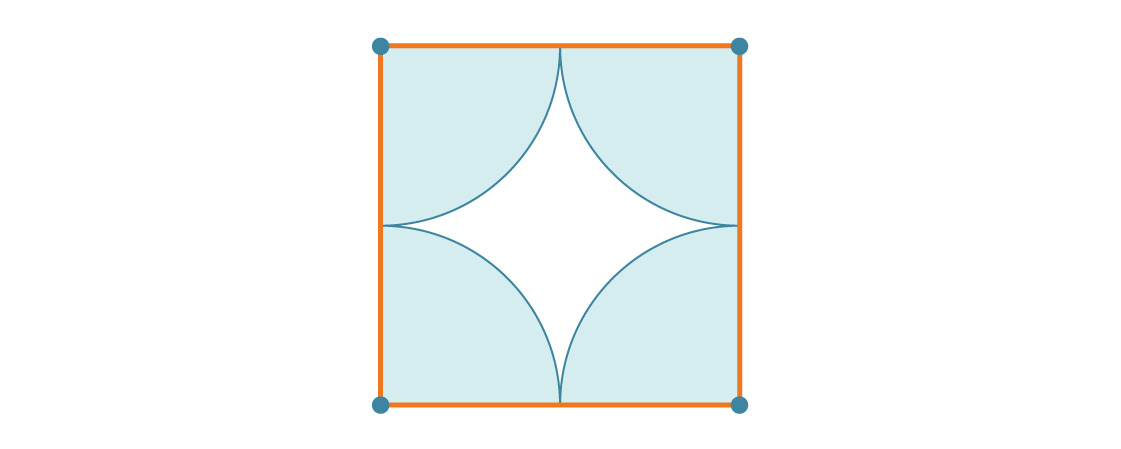
Let's say the radius of the circle is r. This means that the side length of the square is 2r. At each of the vertices of the square there is a quarter of a circle, so the percentage of coverage of each square is simply equal to the ratio of the area of one full circle to the area of one full square:
Each square is about 78.54% covered with circles, so considering the tiling of the plane, it is all about 78.54% covered with circles. This is the density of the square packing. Notice that the radius r disappeared from the answer. And this makes sense: no matter how big the circles are, there will still be four quarters of a circle in a square.
If you tried to fold the soda cans on the side like this, and they slide and fill in the gaps, you know that there is another way to pack the circles on a plane:
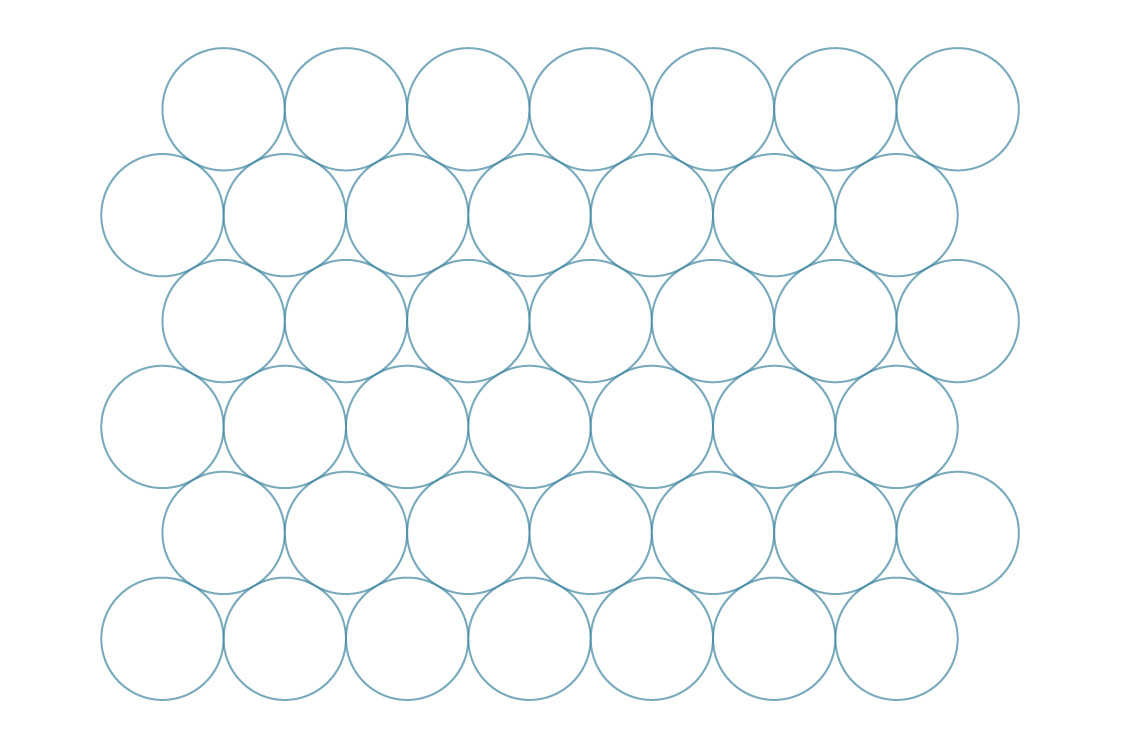
Let's take a similar approach to the previous one, and imagine that the centers of the circles in this case form regular hexagons ...
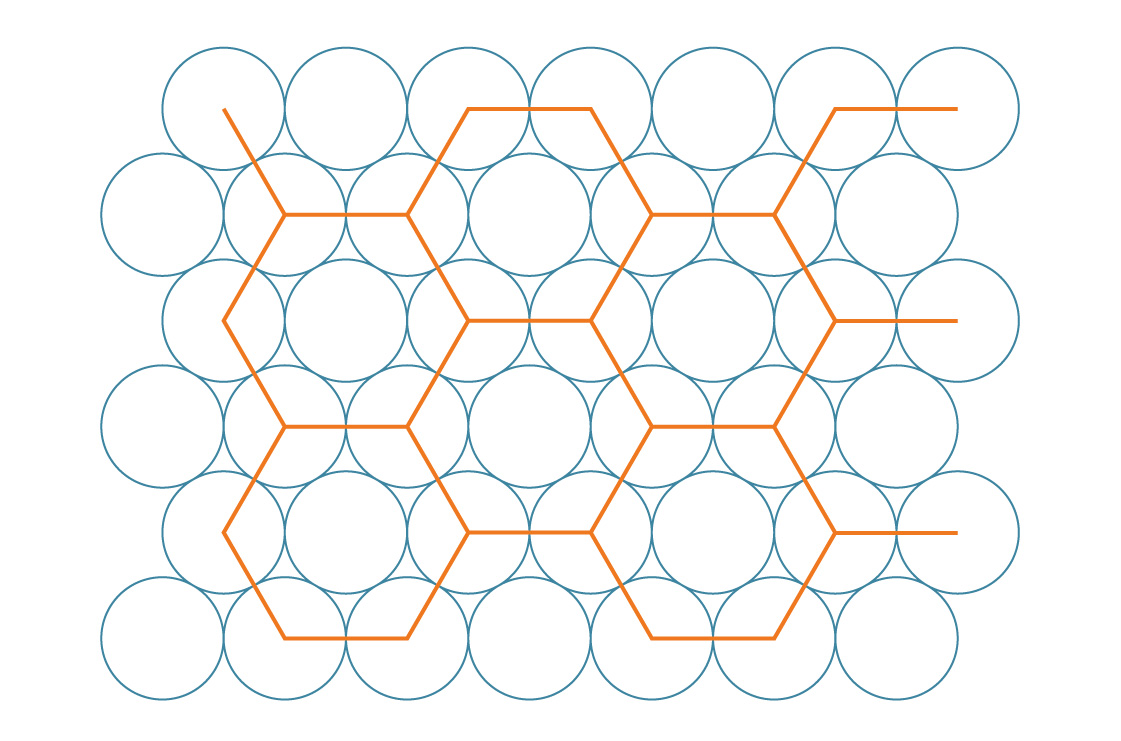
We call this hexagonal packing. It seems that this method fills gaps more efficiently than square. To check this, let's compare their packing densities. Hexagons, like squares, completely tile the plane, so we can determine the density of this method by analyzing a single hexagon.
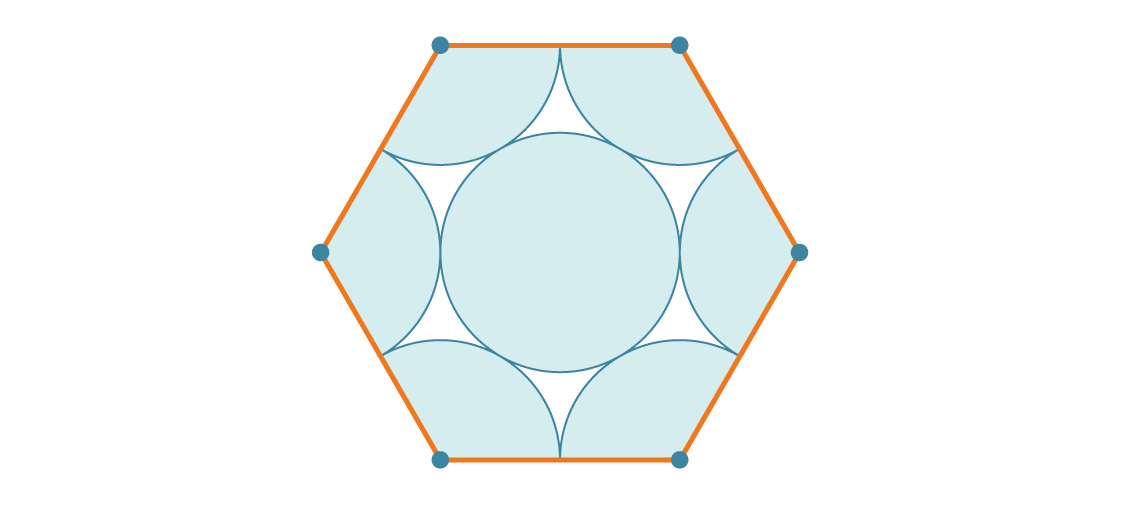
What part of the hexagon is covered with circles? Since a regular hexagon has an inner angle of 120 °, each corner has a third of a circle. It turns out two full circles, and the middle circle goes third. Therefore, each hexagon is covered by three circles. If the radius of each circle is r, then the area is 3πr².
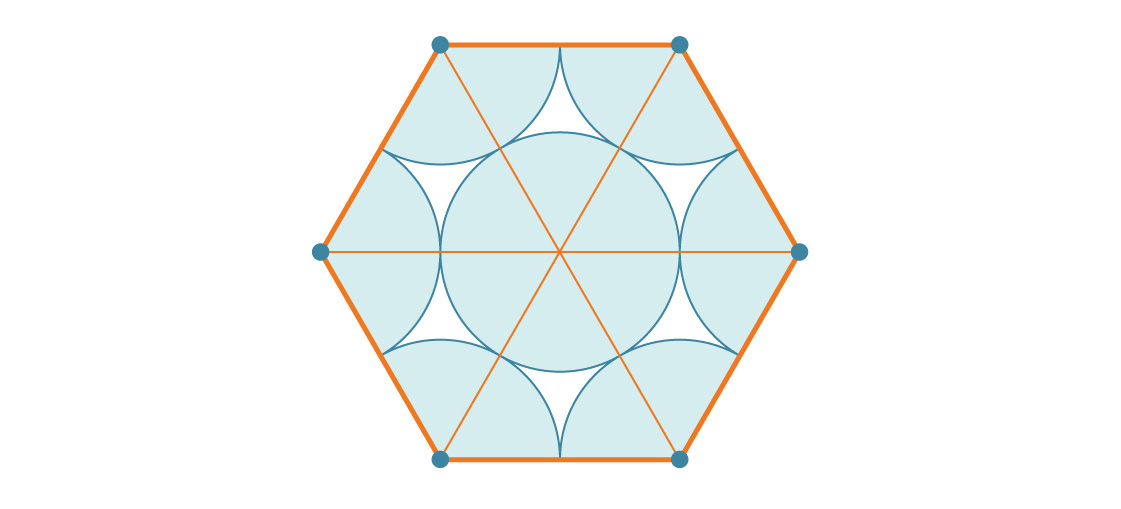
How does this compare to the area of a hexagon? A hexagon with side length s is six equilateral triangles with side length s, each of which is s 2 √3 / 4. Therefore, the area of the hexagon is 6 * s 2 √3 / 4 = 6 s 2 √3 / 4. Since the side length of our hexagon is 2r, its area is:
Now you can calculate the percentage of the hexagon covered by the circles (by dividing the area of the six circles by the area of the hexagon):
Each hexagon is about 90.69% covered with circles, so this packaging will be much more efficient than a square one. Notice how the radius of the circle disappears again as expected. In fact, there is no more efficient packaging.
But it was not easy to prove it. Famous mathematicians such as Joseph Louis Lagrange and Karl Friedrich Gauss began working on this in the late 18th and early 19th centuries, but the problem was completely solved only in the 1940s, by carefully processing all possible arrangements - periodic and non-periodic. The fact that it took so much time to solve the problem in two dimensions, where everything is quite easy to imagine, may serve as a warning to what awaits us in the higher dimensions.
Packing spheres in three dimensions is a much more difficult task, although it bears some similarities to its two-dimensional cousin. For example, the two-dimensional packings we have considered consist of one layer.
For a square package, we put each layer on top of the previous one.
For the hexagonal packing, we placed new layers in between the previous ones.

Different packaging is obtained depending on how we combine copies of different layers.
In three dimensions, this arrangement of layers on top of each other creates fundamentally different packings.
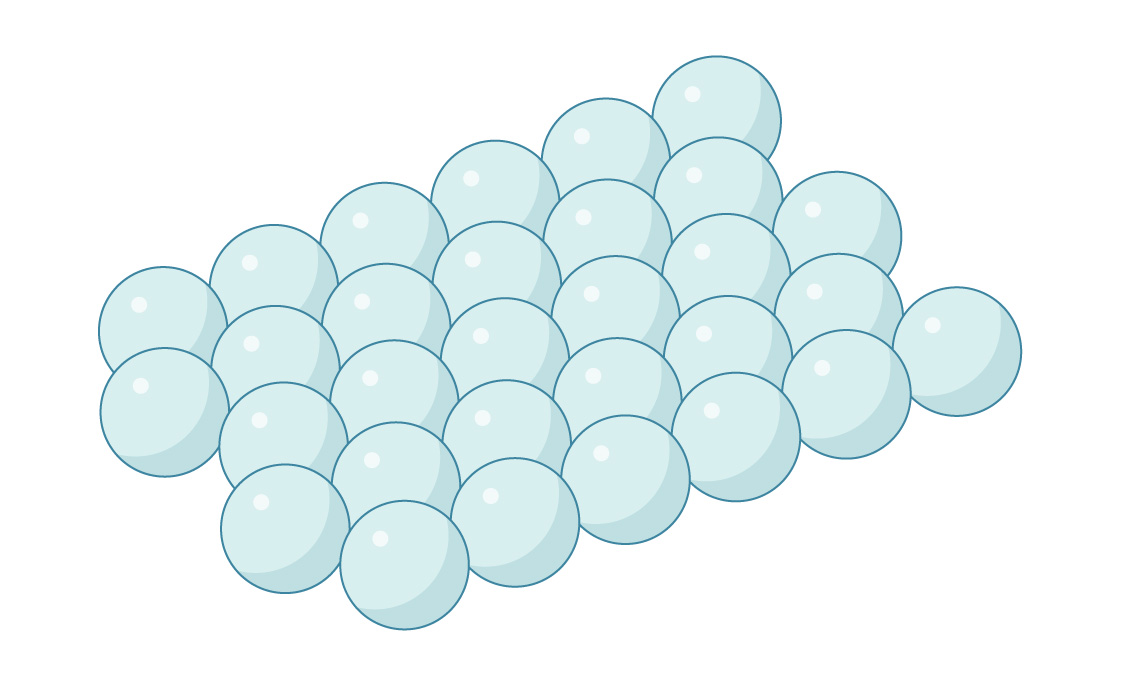
This is a layer of spheres packed hexagonally, as our optimal packing of circles on a plane suggests. Likewise, you can place the second layer on top of the first by placing spheres in the spaces between the lower spheres.

But in three dimensions, the geometry gets a little more complicated. In each layer of spheres, the distance between adjacent gaps turns out to be less than the distance between the centers of the spheres. Therefore, you cannot stick a sphere into each gap - they would intersect. Therefore, the gaps in the two layers line up to create channels that run through the package.

There are two ways to place the third layer. You can align the gaps with the bottom ones, and leave the channels open. Here's a side view of this arrangement:

To keep the channels open, you need to place the spheres in the third layer just above the spheres from the first layer. This arrangement of spheres is called a "hexagonal dense packing" (silo), and if you look at it from above, you can see open gaps going right through.

Another option for placing the third layer is to close the channels. The spheres in the third layer are placed directly above the gaps of the first:
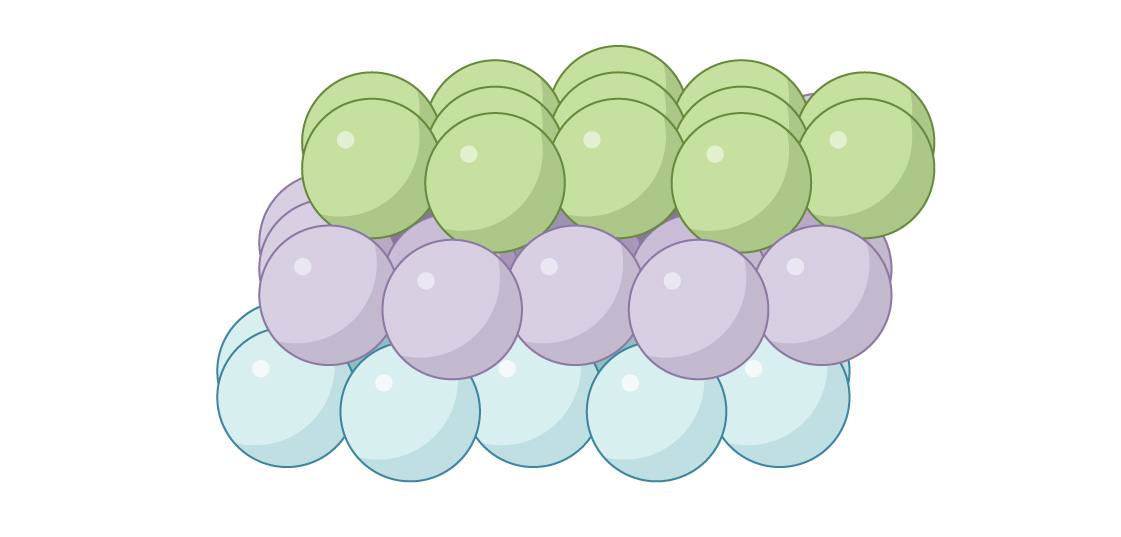
This is called "face-centered cubic" (FCC) or "cubic close packing". When viewed from above, there will be no gaps.
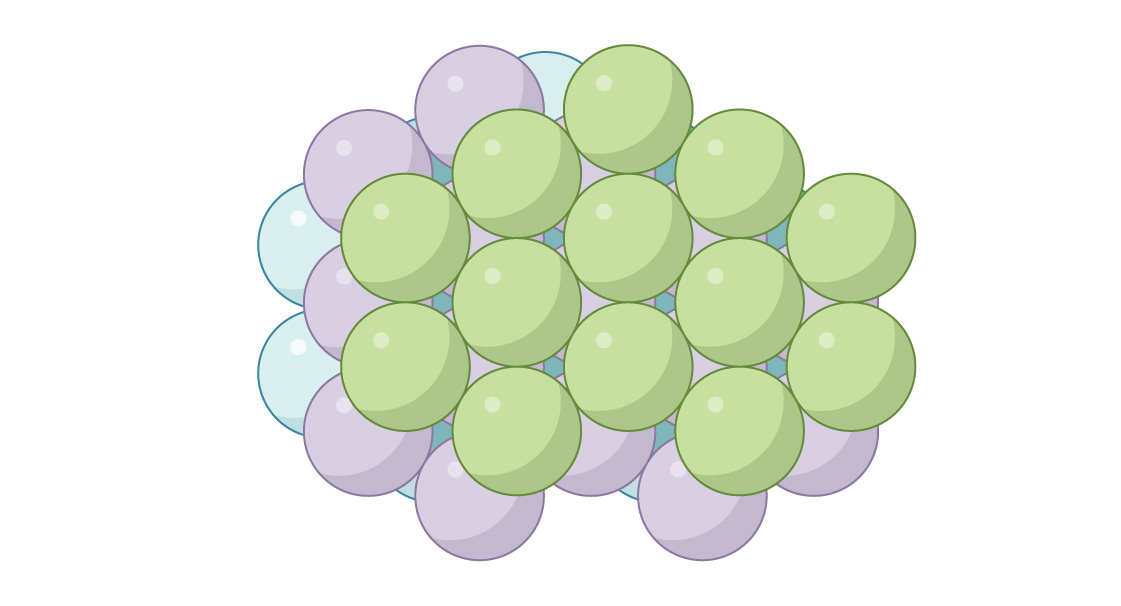
These two similar but fundamentally different arrangements arise in chemistry, describing the arrangement of atoms in different materials. For example, in metals such as silver and gold, the structure has the form of HA, and in metals such as zinc and titanium - silos. Each of the two methods allows you to fill the space with spheres. In the silo method, in every second layer the spheres are located exactly the same, and in the GK - in every third. You can create an infinite number of different packages by combining both of these methods, but it is interesting that both silo and GK give optimal packaging! Their packing density is not only the same, π 3√2 ≈ 0.7405 is the densest possible packing in three-dimensional space. The famous mathematician and astronomer Johannes Kepler suggested this in 1611, but complete proofonly mathematician Thomas Hales was able to deduce in 1998.

There is more room in 3D space, and we have more ways to effectively pack the spheres. When you add dimensions, the complexity of the packaging only increases - there is more space, more options, and it's harder to imagine. Also, the spheres get smaller in higher dimensions!
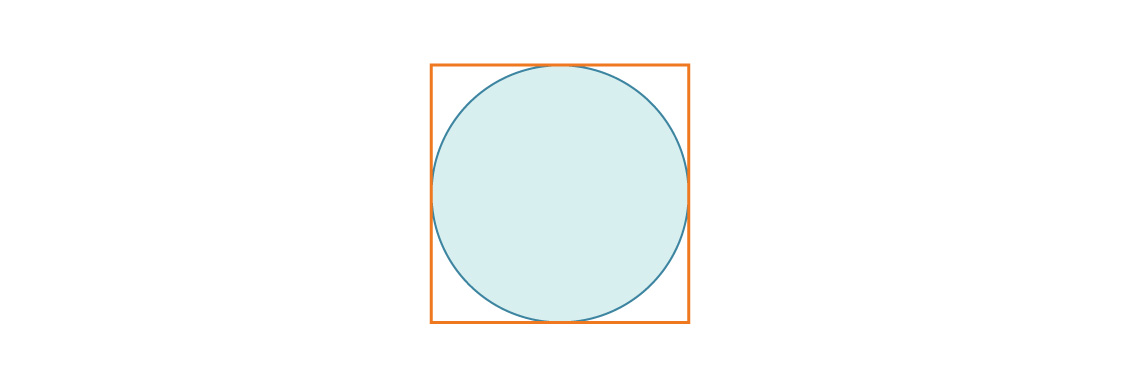
Consider a circle inscribed in a square with side length 1.
The radius of the circle is r = 1/2, so the ratio of the area of the circle to the area of the square is:
Which is also equal to the packing density of the square in two dimensions.
Now let's consider the volume of a sphere inscribed in a unit cube.
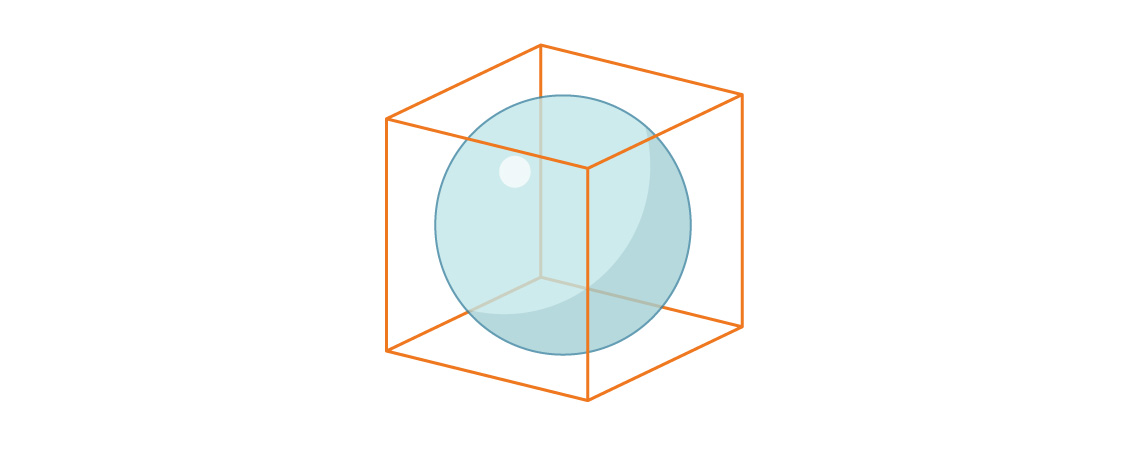
The radius of the sphere is again equal to r = 1/2, so the ratio of the volume of the sphere to the volume of the cube is:
Note that the proportion of the cube occupied by the inscribed sphere in three dimensions is less than the proportion of the square occupied by the inscribed circle in two dimensions. This pattern continues: with increasing dimensions, this ratio decreases. As n grows, n-dimensional spheres occupy less and less n-dimensional space.
This can be shown using algebra, but it can also be understood if you think about angles. In any dimension, an n-dimensional sphere can be inscribed into an n-dimensional cube. The sphere touches the edges of the cube but does not reach the corners, so there is a region around each corner that is inside the cube but outside the sphere. However, an n-dimensional box will have 2 nangles, that is, with an increase in n, the number of areas not covered by the sphere grows exponentially. In addition, the distance between the corners and the sphere also increases. This means that in the long run, the space inside the n-dimensional cube, but outside the n-dimensional sphere, will simply crush the space occupied by the sphere.
If the contraction of the spheres seems strange enough to you, then the mathematicians involved in packing the spheres noticed something even more unexpected in dimensions 8 and 24. In these dimensions, the spheres shrink just enough to be able to fill the gaps between the new spheres, which gives an ultra-dense packing in these dimensions ... It was hypothesized about the optimality of these special methods, but it was not known exactly until 2016, when Marina Vyazovskaya proved this theoremfor 8-dimensional space. A week later, Vyazovskaya and her assistants expanded her method for proving the case of 24-dimensional space as well.
It follows from Vyazovskaya's work that now we know the most efficient ways of packing spheres in dimensions 1, 2, 3, 8 and 24. But in other dimensions there is still a lot of work to do. So get out the oranges and soda cans and start experimenting. You may be the one who can fill in the important gaps.
Exercises
1. Let's say we started packing the coordinate plane as shown in the pictures below. The center of the lower left circle is located at point (0, 0), and the center of the lower right circle is at point (2, 0).
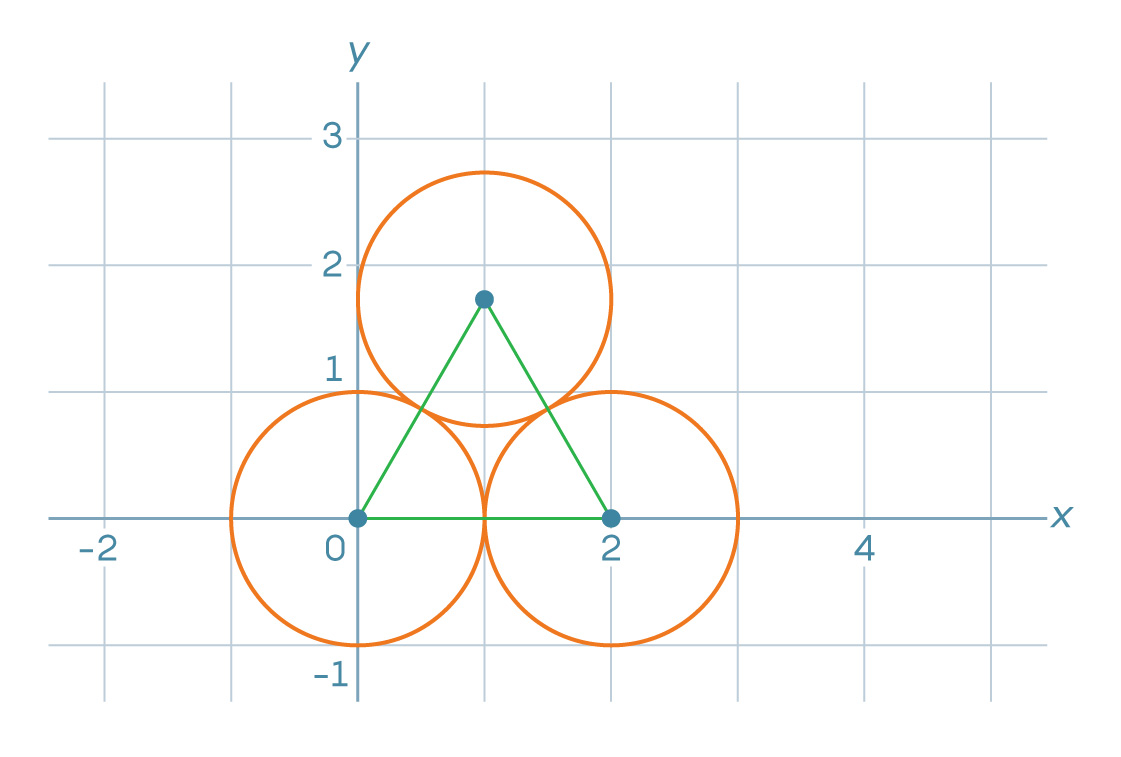
Where is the center of the third circle?
2. Below is the beginning of the "simple cubic" packing of spheres. What is the packing density of such a scheme?

3. Here is the beginning of packing the plane into regular octagons.
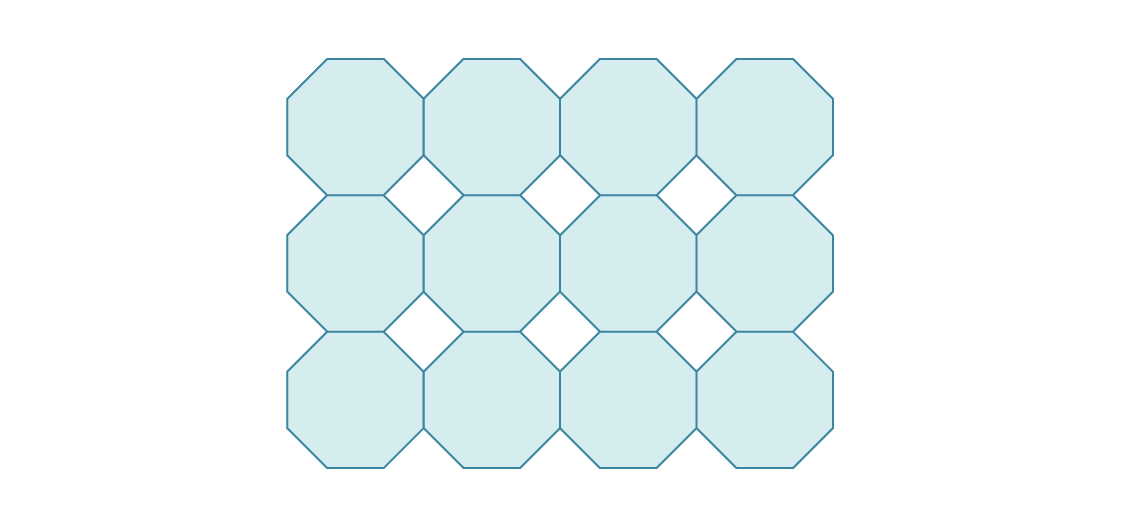
What is the density of such a package?
Answers
Problem 1
2.
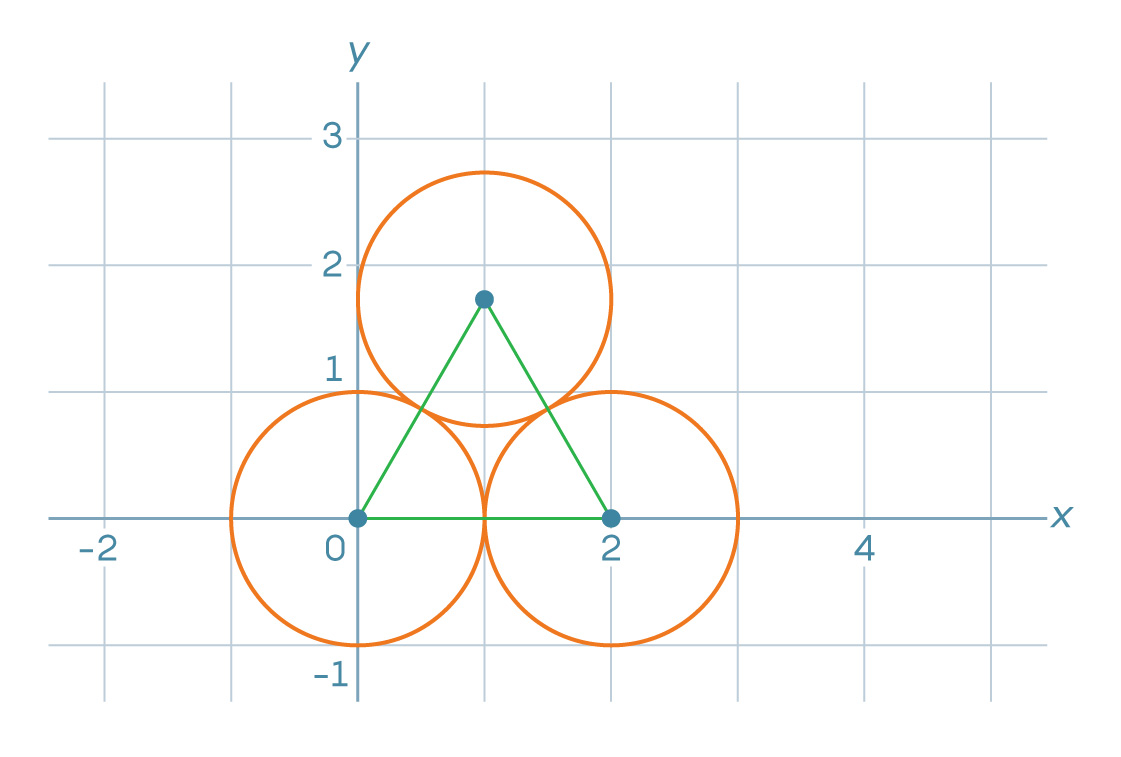
, x 1. s s√3/2, 2√3/2 = √3, y . (1, √3).
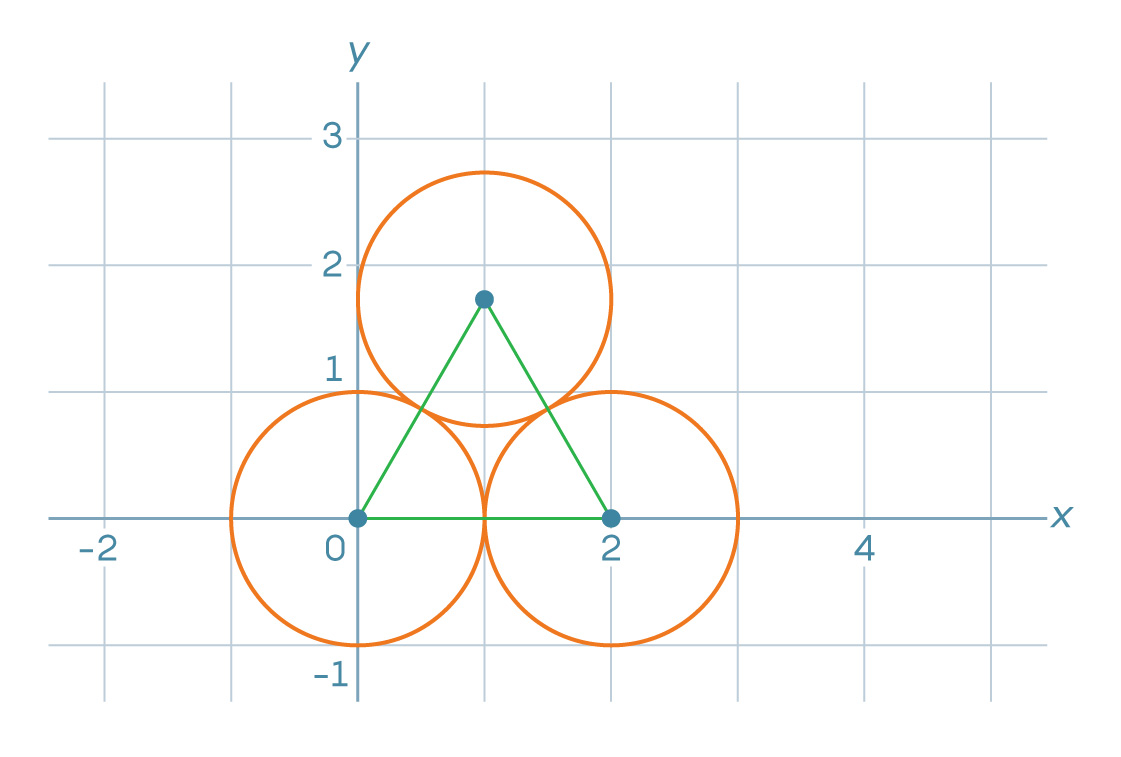
, x 1. s s√3/2, 2√3/2 = √3, y . (1, √3).
Problem 2
, , .

. . r, 2r. ( , ):
, – , .

. . r, 2r. ( , ):
, – , .
Problem 3
, , , , , .

, . s (2+2√2)s2 ( , ), , s. ( , s):
, . ?

, . s (2+2√2)s2 ( , ), , s. ( , s):
, . ?
See also:
- " Google Releases Sodar, An AR Tool for Displaying Social Distance "
- " Meta-study reveals the effectiveness of masks and distancing against SARS-CoV-2 (COVID-19) "
- " COVID-19: Epidemic Parametric Prediction Model "