What is the future of mathematics?
- In the 1990s, computers began to play chess better than humans.
- In 2018, computers are better at playing Go than humans.
- In 2019, artificial intelligence researcher Christian Szegedy told me that in 10 years, computers will be better theorem proving than humans.
Of course, he may be wrong. Or maybe he is right.
I believe in the following: In ten years, computers will help us prove dreary theorems at the level of early graduate students. What areas of mathematics? Depends on who gets involved in this area of research.
The typical pattern for artificial intelligence is this: at first it is very stupid, and then it suddenly gets smarter. The natural question is: when does the phase transition occur and the artificial intelligence suddenly becomes very smart? Answer: nobody knows this. What is clear is that the more people are involved in this area of research, the sooner this will happen.
What is proof?
If you ask an excellent student, a research mathematician, and a computer what proof is, what is their answer? The answers of the excellent student and the computer will coincide and will be as follows:
— , , , , , , .Of course, the answer of a research mathematician would not be so idealistic. For a mathematician, the definition of proof is what other experienced mathematicians regard as proof. Or what is accepted for publication in the Annals of Mathematics or Inventiones.
However, there is a small problem with this. The following screenshots are taken from the website of the Annals of Mathematics , one of the most prestigious mathematical journals in the world.
The second article literally contradicts the first. The authors openly write about this in the annotation. As far as I know, the Annals of Mathematics has never published a rebuttal to any of these works. Which work is considered correct by experienced mathematicians? You can only find out about this if you work in this field.
Output: in modern mathematics, the opinion about whether something is proof changes over time (for example, it can go from “is” to “is not”).
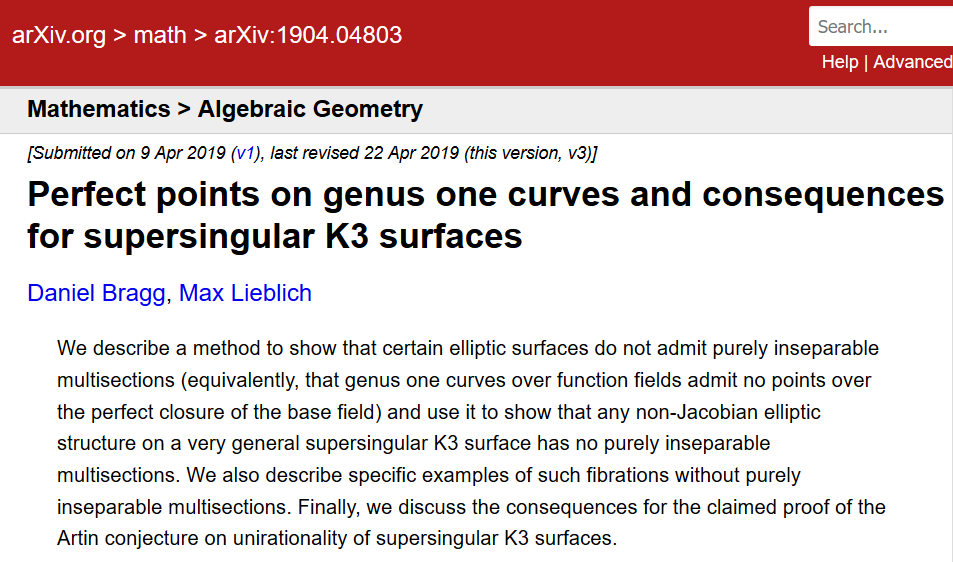
This short 2019 article points out that another important 2015 article published in Inventiones relies heavily on a false lemma. This was not noticed until 2019, despite the fact that in 2016 people held workshops to study this important work.
Vladimir Voevodsky, a Fields Prize laureate who contributed to the foundations of mathematics, writes that “if an author who is trusted by people writes a technically complex argument that is difficult to verify, but which is similar to other, correct arguments, then this argument will hardly ever anything will be checked in detail at all. "
Inventiones never published a refutation of the 2015 paper.
Conclusion : The important math that has been published sometimes turns out to be wrong. Moreover, in the future we will surely see more rebuttals of the published evidence.
Maybe my work in the p-adic Langlands program is based on incorrect results. Or, more optimistically, for correct results, but for which there is no complete proof.
If our research is irreproducible, can we call it science? I'm 99.9% sure that Langlands' p-adic program will never be used by humanity to do anything useful. If my work in math is not helpful and guaranteed to be 100 percent correct, it’s just a waste of time.... So I decided to stop researching and concentrate on testing “famous” mathematics on a computer.
In 2019, Balakrishnan, Dogra, Mueller, Tuitman, and Vonk found all rational solutions to a certain fourth degree equation in two variables. Explicitly:
This calculation has an important application in arithmetic. The proof relies heavily on computation in magma (a closed source system) using fast, unreferenced algorithms. It would be difficult to port all the computing to an open source system like sage. However, no one plans to do this.
Thus, some of the evidence remains hidden. And perhaps it will remain hidden forever. Is this science?
Gaps in math
- 1993 . .
- 1994 , .
- 1995 , , . , , , . , , , .
What should a reviewer who receives a mathematical article for review do? It is argued that the reviewer's job is to “make sure that the methods used in the paper are strong enough to prove the main result of the paper.”
What if the methods are strong, but the authors are not? This is how situations arise when our evidence is incomplete. This is how the debate arises about whether our theorems are actually proven. This is not at all how we teach our students about mathematics.
Of course, experts know which literature can be trusted and which cannot. But do I have to be an expert to know which literature I can trust?
Big gaps in math
Exhibit A
Classification of simple finite groups . Experts claim that we have a complete classification of simple finite groups. I trust the experts.
- In 1983, a proof of classification by experts was announced.
- In 1994, experts found a mistake (but let's not blow the elephant out of a fly?)
- In 2004, 1000+ page work was published. Field expert Aschbacher claims the error has been corrected and announces a plan to publish 12 volumes of full proof.
- In 2005, only 6 of 12 volumes were published
- In 2010, only 6 of 12 volumes were published
- In 2017, only 6 of 12 volumes were published
- In 2018, the 7th and 8th volumes were published and a note that the publication will be completed by 2023.
Of the three people leading the project, one died. The other two are over seventy.
Exhibit B
Potential modularity of abelian surfaces . A year ago, my distinguished graduate student Toby Gee and three coauthors published a 285-page preprint with the result that Abelian surfaces over completely real fields are potentially modular.
Their proof cites three unpublished preprints (one in 2018, one in 2015, one in the 1990s), an Internet memo from 2007, an unpublished dissertation in German, and a paper whose main claim was later refuted. Moreover, on page 13 we see the following text:
, Arthur’s multiplicity formula GSp4, [Art04]. , , [GT18], , [Art13] [MW16a, MW16b]. , twisted weighted fundamental lemma, [CL10], . , [A24], [A25], [A26] [A27] [Art13], .Can we honestly say that this is science?
Link [CL10] looks like this: The
work that my graduate student and co-authors need has never been published. Most likely, the statement is correct. Perhaps even provable.
And these are the referenced links from [Art13]:
Last year I asked Arthur about these links, and he told me that none of the work was ready yet. Of course, Jim Arthur is a genius. He has won numerous prestigious awards. But he's also 75 years old.
Exhibit C
Gaitsgory – Rozenblyum . Endless categories have gained popularity lately. Over time, they will become even more important. The work of Fields laureate Peter Scholze rests on endless categories.
Jacob Lurie has written a 1000+ page work about
-categorized and included a lot of detail in my work. Gaitsgory – Rozenblyum wanted similar results for
-categories, but omitted many of the arguments to save time. "The omitted evidence will appear elsewhere."
I asked Gaitsgory how much was missing. He replied that it was about 100 pages. I asked Lurie what he thinks about this. He replied that "mathematicians differ greatly in how comfortable they are with omitting details."
Is the math moving too fast? If I am an “expert”, should I believe that Abelian surfaces over totally real fields are potentially modular? To be honest, I don't know myself anymore.
At a conference at Carnegie Mellon University where I was last week, Markus Rabe told me that Google is working on a program that will translate math preprints from arxiv.orginto a language suitable for computer verification. I also recently saw work that relies on an article by my student, but does not mention anything about the missing 100 pages in [Art13].
Last mistake
This is a very interesting example. The original work was published in J. Funct. Anal. in 2013. There is a big error in the work (inequality in the other direction). The error was discovered by S. Gouezel in 2017, when Gouezel formalized an argument using a computerized proof-checking program (Isabelle).
A new argument is presented by Gouezel and the author of the original work. New work does not need reviewing. The computer checked 100 percent of the new argument. The methods turned out to be strong enough to prove the theorem. And by “proof” I mean the classic, “pure” definition of proof — that which we teach our students. Every detail of the proof is available to the reader. Science is reproducible. This is the mathematics we teach our students. This is mathematics.
Here are other examples of what I think is math:
- Typical Proof of Student or Master's Level
- Typical 100-year-old proof of an important result that has been well-documented and researched by tens of thousands of mathematicians
- Formal proof of Gonthier, Asperti, Avigad, Bertot, Cohen, Garillot, Le Roux, Mahboubi, O'Connor, Ould Biha, Pasca, Rideau, Solovyev, Tassi, Théry of the Feith-Thompson theorem.
- Formal proof of authorship by the following mathematicians: Hales, Adams, Bauer, Dat Tat Dang, Harrison, Truong Le Hoang, Kaliszyk, Magron, McLaughlin, Thang Tat Nguyen, Truong Quang Nguyen, Nipkow, Obua, Pleso, Rute, Solovyev, An Hoai Thi Ta , Trung Nam Tran, Diep Thi Trieu, Urban, Ky Khac Vu, and Zumkeller's proof of Kepler's conjecture.
This concludes the text of the presentation, because Kevin moves on to his main part: the formal verification of mathematical proofs in Lean, developed by Leo de Moura at Microsoft Research. Unfortunately, examples were not included in the slides.
The author is a huge enthusiast for formal verification of mathematical proofs and has a very interesting Xena blog on this topic that I highly recommend.