
Information security problems require the study and solution of a number of theoretical and practical problems in the information interaction of system subscribers. Our doctrine of information security formulates the triune task of ensuring the integrity, confidentiality and availability of information. The articles presented here are devoted to the consideration of specific issues of its solution within the framework of various state systems and subsystems. Earlier, the author considered in 5 articles the issues of ensuring the confidentiality of messages by means of state standards. The general concept of the coding system was also given by me earlier .
Introduction
By my basic education, I am not a mathematician, but in connection with the disciplines I read at the university, I had to meticulously understand it. For a long time and persistently I read the classic textbooks of our leading Universities, a five-volume mathematical encyclopedia, many thin popular brochures on specific issues, but satisfaction did not arise. Deep reading comprehension did not arise either.
All mathematical classics are focused, as a rule, on the infinite theoretical case, and special disciplines are based on the case of finite constructions and mathematical structures. The difference in approaches is colossal, the absence or lack of good complete examples is perhaps the main disadvantage and lack of university textbooks. There is very rarely a problem book with solutions for beginners (for freshmen), and those that do exist sin with omissions in explanations. In general, I fell in love with second-hand technical book stores, thanks to which the library and, to a certain extent, the store of knowledge were replenished. I had a chance to read a lot, a lot, but "did not go".
This path led me to the question, what can I already do on my own without book "crutches", having in front of me only a blank sheet of paper and a pencil with an eraser? It turned out to be quite a bit and not quite what was needed. The difficult path of haphazard self-education was passed. The question was this. Can I build and explain, first of all to myself, the work of code that detects and fixes errors, for example, Hamming code, (7, 4) -code?
It is known that Hamming code is widely used in many applications in the field of data storage and exchange, especially in RAID; in addition, it is in ECC memory and allows on-the-fly correction of single and double errors.
Information Security. Codes, ciphers, steg messages
Information interaction through the exchange of messages between its participants should be provided with protection at different levels and by various means, both hardware and software. These tools are developed, designed and created within the framework of certain theories (see Figure A) and technologies adopted by international agreements on OSI / ISO models.
Information security in information telecommunication systems (ITS) is becoming practically the main problem in solving management problems, both on the scale of an individual - user, and for firms, associations, departments and the state as a whole. Of all the aspects of ITKS protection, in this article we will consider the protection of information during its extraction, processing, storage and transmission in communication systems.
Further clarifying the subject area, we will focus on two possible directions in which two different approaches to the protection, presentation and use of information are considered: syntactic and semantic. The figure uses abbreviations: codec – codec – decoder; shidesh - a decoder-decoder; screech - concealer - extractor.
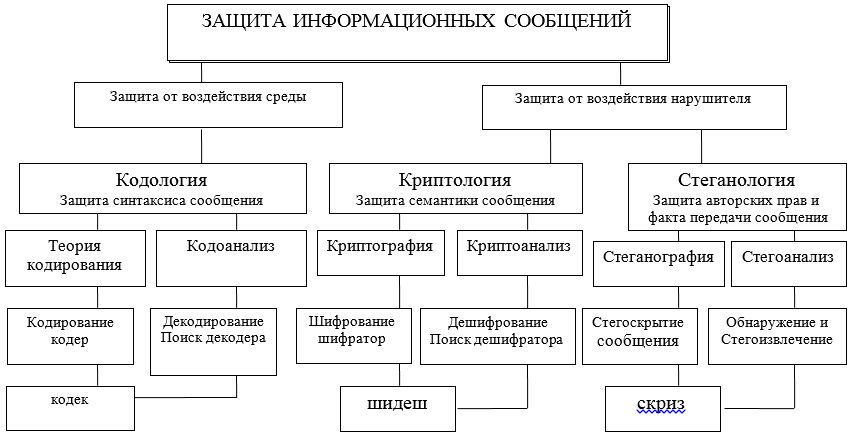
Figure A - Diagram of the main directions and interrelationships of theories aimed at solving problems of protecting information interaction
The syntactic features of the presentation of messages allow you to control and ensure the correctness and accuracy (error-free, integrity) of the presentation during storage, processing, and especially when transmitting information through communication channels. Here, the main problems of protection are solved by the methods of codology, its large part - the theory of correcting codes.
Semantic (semantic) securitymessages are provided by methods of cryptology, which by means of cryptography makes it possible to protect a potential intruder from mastering the content of information. In this case, the violator can copy, steal, change or replace, or even destroy the message and its carrier, but he will not be able to obtain information about the content and meaning of the message being transmitted. The content of the information in the message will remain inaccessible to the offender. Thus, the subject of further consideration will be syntactic and semantic protection of information in ITCS. In this article, we will restrict ourselves to considering only the syntactic approach in a simple, but very important implementation of it by correcting code.
I will immediately draw a dividing line in solving information security problems: the
theory of codologydesigned to protect information (messages) from errors (protection and analysis of the syntax of messages) of the channel and the environment, to detect and correct errors;
the theory of cryptology is designed to protect information from unauthorized access to its semantics by the intruder (protection of semantics, the meaning of messages);
the theory of steganology is designed to protect the fact of information exchange of messages, as well as to protect copyright, personal data (protection of medical secrecy).
In general, let's go. By definition, and there are quite a few of them, it is not even easy to understand that there is code. The authors write that the code is an algorithm, a display, and something else. I will not write about the classification of codes here, I will only say that the (7, 4) -code is block .
At some point, it dawned on me that the code is special code words, a finite set of them, which are replaced by special algorithms with the original text of the message on the transmitting side of the communication channel and which are sent through the channel to the recipient. The replacement is performed by the encoder device, and on the receiving side these words are recognized by the decoder device.
Since the role of the parties is changeable, both of these devices are combined into one and called the abbreviated codec (encoder / decoder), and are installed at both ends of the channel. Further, since there are words, there is also an alphabet. The alphabet is two characters {0, 1}, block binarycodes. The natural language alphabet (NL) is a set of symbols - letters that replace the sounds of oral speech when writing. Here we will not delve into hieroglyphic writing in syllabic or nodular writing.
The alphabet and words are already a language, it is known that natural human languages are redundant, but what this means, where language redundancy dwells is hard to say, redundancy is not very well organized, chaotic. When coding, storing information, they tend to reduce redundancy, for example, archivers, Morse code, etc.
Richard Hemming probably realized earlier than others that if redundancy is not eliminated, but reasonably organized, then it can be used in communication systems to detect errors and automatically correct them in the code words of the transmitted text. He realized that all 128 seven-bit binary words can be used to detect errors in codewords that form a code - a subset of 16 seven-bit binary words. It was a brilliant guess.
Before the invention of Hamming, errors were also detected by the receiving side when the decoded text could not be read or it turned out not quite what was needed. In this case, a request was sent to the sender of the message to repeat the blocks of certain words, which, of course, was very inconvenient and slowed down communication sessions. This was a big problem that had not been solved for decades.
Construction of a (7, 4) Hamming code
Let's go back to Hamming. Words of the (7, 4) -code are formed from 7 bits j =, j = 0 (1) 15, 4-information and 3-check symbols, i.e. essentially redundant, since they carry no message information. It was possible to represent these three check digits by linear functions of 4 information symbols in each word, which ensured the detection of the fact of an error and its place in words in order to make a correction. A (7, 4) -code got a new adjective and became a linear block binary .
Linear functional dependencies (rules (*)) for calculating symbol values
look like this:
Correcting the error became a very simple operation - a character (zero or one) was determined in the erroneous bit and replaced with another opposite 0 by 1 or 1 by 0.
How many different words form the code? The answer to this question for the (7, 4) -code is very simple. Since there are only 4 information digits, and their variety, when filled with symbols, has= 16 options, then there are simply no other possibilities, that is, a code consisting of only 16 words ensures that these 16 words represent the entire writing of the entire language.
The informational parts of these 16 words are numbered #
():
0 = 0000; 4 = 0100; 8 = 1000; 12 = 1100;
1 = 0001; 5 = 0101; 9 = 1001; 13 = 1101;
2 = 0010; 6 = 0110; 10 = 1010; 14 = 1110;
3 = 0011; 7 = 0111; 11 = 1011; 15 = 1111.
Each of these 4-bit words needs to be calculated and added to the right by 3 check bits, which are calculated according to the rules (*). For example, for information word No. 6 equal to 0110, we have and evaluating the check characters gives the following result for this word:
In this case, the sixth code word takes the form: In the same way it is necessary to calculate check symbols for all 16 codewords. Let's prepare a 16-line table K for the code words and sequentially fill in its cells (I recommend the reader to do this with a pencil in hand).
Table K - codewords j, j = 0 (1) 15, (7, 4) - Hamming codes
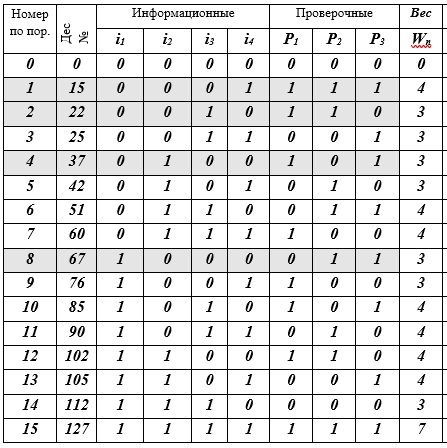
Description of the table: 16 lines - code words; 10 columns: sequence number, decimal representation of the code word, 4 information symbols, 3 check symbols, the W-weight of the code word is equal to the number of non-zero bits (≠ 0). 4 code words-lines are highlighted by filling - this is the basis of the vector subspace. Actually, that's all - the code is built.
Thus, the table contains all the words (7, 4) - the Hamming code. As you can see, it was not very difficult. Next, we will talk about what ideas led Hamming to this code construction. We are all familiar with Morse code, with the naval semaphore alphabet and other systems built on different heuristic principles, but here in (7, 4) -code, rigorous mathematical principles and methods are used for the first time. The story will be just about them.
Mathematical foundations of the code. Higher algebra
The time has come to tell how R. Hemming came up with the idea of opening such a code. He had no special illusions about his talent and modestly formulated a task for himself: to create a code that would detect and correct one error in each word (in fact, even two errors were detected, but only one of them was corrected). With quality channels, even one mistake is a rare event. Therefore, Hemming's plan was still grandiose on the scale of the communications system. There was a revolution in coding theory after its publication.
It was 1950. I am giving here my simple (I hope, understandable) description, which I have not seen from other authors, but as it turned out, everything is not so simple. It took knowledge from numerous areas of mathematics and time to deeply understand everything and understand for yourself why this is done this way. Only after that I was able to appreciate the beautiful and rather simple idea that is implemented in this correcting code. Most of the time I spent on dealing with the technique of calculations and the theoretical justification of all the actions that I am writing about here.
The creators of the codes, for a long time, could not think of a code that detects and corrects two errors. The ideas used by Hemming did not work there. I had to look, and new ideas were found. Very interesting! Captivates. It took about 10 years to find new ideas, and only after that there was a breakthrough. Codes showing an arbitrary number of errors were received relatively quickly.
Vector spaces, fields and groups . The resulting (7, 4) -code (Table K) represents a set of codewords that are elements of a vector subspace (of order 16, with dimension 4), i.e. part of a vector space of dimension 7 with orderOf the 128 words, only 16 are included in the code, but they were included in the code for a reason.
First, they are a subspace with all the ensuing properties and singularities; second, codewords are a subgroup of a large group of order 128, even moreover, an additive subgroup of a finite extended Galois field GF () degree of expansion n = 7 and characteristic 2. This large subgroup is decomposed into adjacent classes by a smaller subgroup, which is well illustrated by the following table D. The table is divided into two parts: upper and lower, but it should be read as one long one. Each adjacent class (row of the table) is an element of the factor group by the equivalence of components.
Table D - Decomposition of the additive group of the Galois field GF () into cosets (rows of Table D) for the 16th order subgroup.
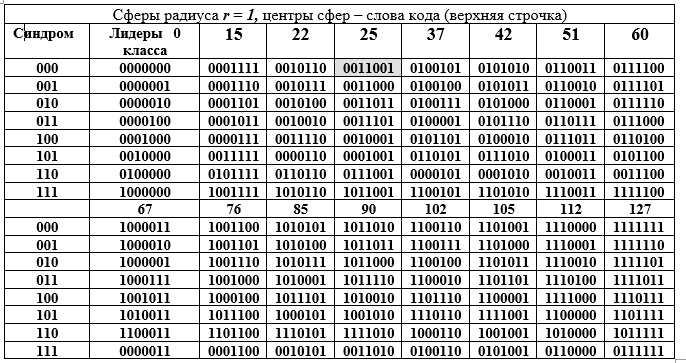
The columns of the table are spheres of radius 1. The left column (repeated) is the syndrome of the word (7, 4) Hamming code, the next column is the leaders of the contiguous class. Let's open the binary representation of one of the elements (the 25th is highlighted by filling) of the factor group and its decimal representation:
Technique of obtaining rows of table D. An element from the column of leaders of the class is summed with each element from the header of the column of table D (summation is performed for the leader's row in binary form mod2). Since all class leaders have a weight W = 1, then all the sums differ from the word in the column heading in only one position (the same for the entire row, but different for the column). Table D has a wonderful geometric interpretation. All 16 codewords are represented by the centers of the spheres in the 7-dimensional vector space. All words in the column differ from the upper word in the same position, that is, they lie on the surface of a sphere with radius r = 1.
This interpretation hides the idea of detecting one error in any code word. We work with spheres. The first condition for error detection is that spheres of radius 1 should not touch or intersect. This means that the centers of the spheres are at a distance of 3 or more from each other. In this case, the spheres not only do not intersect, but also do not touch one another. This is a requirement for the unambiguity of the decision: which sphere should be attributed to the erroneous word received on the receiving side by the decoder (not the code one of 128 -16 = 112).
Second, the entire set of 7-bit binary words of 128 words is evenly distributed over 16 spheres. The decoder can only get a word from this set of 128 known words with or without error. Third, the receiving side can receive a word without error or with distortion, but always belonging to one of the 16 spheres, which is easily determined by the decoder. In the latter situation, a decision is made that a code word was sent - the center of a sphere determined by the decoder, which found the position (intersection of a row and a column) of the word in table D, i.e., the column and row numbers.
Here a requirement arises for the words of the code and for the code as a whole: the distance between any two codewords must be at least three, that is, the difference for a pair of codewords, for example, i = 85 == 1010101; j = 25 == 0011001 must be at least 3; 85 - 25 = 1010101 - 0011001 = 1001100 = 76, the weight of the difference word W (76) = 3. (Table E replaces the calculation of differences and sums). Here, the distance between binary word vectors is understood as the number of non-matching positions in two words. This is the Hamming distance, which has become widely used in theory and in practice, since it satisfies all the axioms of distance.
Remark . The (7, 4) -code is not only a linear block binary code , but it is also a group code, that is, the words of the code form an algebraic group by addition. This means that any two codewords, when added together, again give one of the codewords. Only this is not an ordinary addition operation, it is addition modulo two.
Table E - The sum of the elements of the group (codewords) used to construct the Hamming code
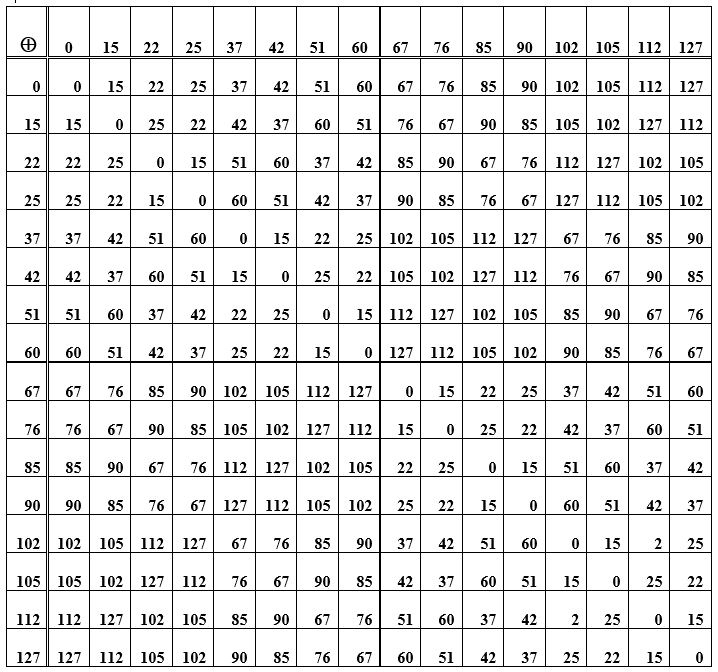
The operation of summing words itself is associative, and for each element in the set of codewords there is an opposite to it, i.e., summing the original word with the opposite gives zero value. This zero codeword is the neutral element in the group. In table D, this is the main diagonal of zeros. The rest of the cells (row / column intersections) are numbers-decimal representations of code words obtained by summing elements from a row and a column. When you rearrange the words in places (when adding), the result remains the same, moreover, subtraction and addition of words have the same result. Further, an encoding / decoding system that implements the syndromic principle is considered.
Code application. Coder
The encoder is located on the transmitting side of the channel and is used by the sender of the message. The sender of the message (the author) forms the message in the natural language alphabet and presents it in digital form. (The name of the character in ASCII code and in binary).
It is convenient to generate texts in files for a PC using a standard keyboard (ASCII codes). Each character (letter of the alphabet) corresponds to an octet of bits (eight bits) in this encoding. For the (7, 4) - Hamming code, in the words of which there are only 4 information symbols, when encoding a keyboard symbol into a letter, two code words are required, i.e. an octet of a letter is split into two information words of the natural language (NL) of the form
...
Example 1 . It is necessary to transfer the word "digit" in NL. We enter the ASCII code table, the letters correspond to: c –11110110, and –11101000, f - 11110100, p - 11110000, and - 11100000 octets. Or otherwise, in ASCII codes, the word "digit" = 1111 0110 1110 1000 1111 0100 1111 0000 1110 0000
with a breakdown into tetrads (4 digits each). Thus, encoding the word "digit" NL requires 10 codewords of the (7, 4) Hamming code. The tetrads represent the informational bits of the message words. These information words (tetrads) are converted into code words (7 bits each) before being sent to the communication network channel. This is done by vector-matrix multiplication: the information word by the generating matrix. The payment for convenience is very expensive and lengthy, but everything works automatically and, most importantly, the message is protected from errors.
The generating matrix of the (7, 4) Hamming code or the code word generator is obtained by writing out the basis vectors of the code and combining them into a matrix. This follows from the theorem of linear algebra: any vector of a space (subspace) is a linear combination of basis vectors, i.e. linearly independent in this space. This is exactly what is required - to generate any vectors (7-bit code words) from information 4-bit ones.
The generating matrix of the (7, 4, 3) Hamming code or the code word generator has the form:
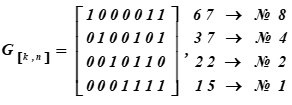
On the right are the decimal representations of the code words of the Basis of the subspace and their ordinal numbers in the table K
No. i rows of the matrix are the code words that are the basis of the vector subspace.
An example of coding words of information messages (the generating matrix of the code is built from the basis vectors and corresponds to the part of the table K). In the ASCII code table, we take the letter q = <1111 0110>.
Information words of the message look like:
...
These are half of the character (c). For the (7, 4) -code defined earlier, it is required to find the code words corresponding to the information message-word (c) of 8 characters in the form:
...
To turn this letter-message (q) into codewords u, each half of the letter-message i is multiplied by the generating matrix G [k, n] of the code (matrix for table K):
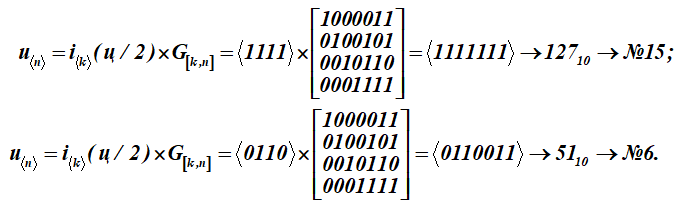
We got two codewords with serial numbers 15 and 6.
Show detailed formation of the lower result No. 6 - a code word (multiplication of a row of an information word by the columns of a generating matrix); summation over (mod2)
<0110> ∙ <1000> = 0 ∙ 1 + 1 ∙ 0 + 1 ∙ 0 + 0 ∙ 0 = 0 (mod2);
<0110> ∙ <0100> = 0 ∙ 0 + 1 ∙ 1 + 1 ∙ 0 + 0 ∙ 0 = 1 (mod2);
<0110> ∙ <0010> = 0 ∙ 0 + 1 ∙ 0 + 1 ∙ 1 + 0 ∙ 0 = 1 (mod2);
<0110> ∙ <0001> = 0 ∙ 0 + 1 ∙ 0 + 1 ∙ 0 + 0 ∙ 1 = 0 (mod2);
<0110> ∙ <0111> = 0 ∙ 0 + 1 ∙ 1 + 1 ∙ 1 + 0 ∙ 1 = 0 (mod2);
<0110> ∙ <1011>= 0 ∙ 1 + 1 ∙ 0 + 1 ∙ 1 + 0 ∙ 1 = 1 (mod2);
<0110> ∙ <1101> = 0 ∙ 1 + 1 ∙ 1 + 1 ∙ 0 + 0 ∙ 1 = 1 (mod2).
Received as a result of multiplication the fifteenth and sixth words from Table K. The first four bits in these code words (multiplication results) represent information words. They look like:, (in the ASCII table it is only half of the letter t). For the coding matrix, a set of words with numbers: 1, 2, 4, 8 are selected as basis vectors in table K. In the table they are highlighted by filling. Then for this table K the coding matrix will receive the form G [k, n].
As a result of multiplication, 15 and 6 words of the K code table were obtained.
Code application. Decoder
The decoder is located on the receiving side of the channel where the receiver of the message is. The purpose of the decoder is to provide the recipient with the transmitted message in the form in which it existed at the sender at the time of sending, i.e. the recipient can use the text and use the information from it for their further work.
The main task of the decoder is to check whether the received word (7 bits) is the one that was sent on the transmitting side, whether the word contains errors. To solve this problem, for each word received by the decoder, by multiplying it by the check matrix H [nk, n], a short vector syndrome S (3 bits) is calculated.
For words that are code, that is, do not contain errors, the syndrome always takes a zero value S = <000>. For a word with an error, the syndrome is not zero S ≠ 0. The value of the syndrome makes it possible to detect and localize the position of the error up to a bit in the word received on the receiving side, and the decoder can change the value of this bit. In the check matrix of the code, the decoder finds a column that coincides with the value of the syndrome, and the ordinal number of this column is equal to the bit corrupted by the error. After that, for binary codes, the decoder changes this bit - just replace it with the opposite value, that is, one is replaced by zero, and zero is replaced by one.
The code in question is systematic, that is, the symbols of the information word are placed in a row in the most significant bits of the code word. Recovery of information words is performed by simple discarding of the least significant (check) bits, the number of which is known. Next, a table of ASCII codes is used in reverse order: the input is information binary sequences, and the output is the letters of the natural language alphabet. So, the (7, 4) -code is systematic, group, linear, block, binary .
The basis of the decoder is formed by the check matrix H [nk, n], which contains the number of rows equal to the number of check symbols, and all possible columns, except for zero, columns of three characters... The parity check matrix is constructed from the words of the table K, they are chosen so as to be orthogonal to the coding matrix, i.e. their product is the zero matrix. The check matrix takes the following form in multiplication operations, it is transposed. For a specific example, the check matrix H [nk, n] is given below:
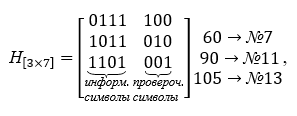



We see that the product of the generating matrix and the check matrix results in a zero matrix.
Example 2. Decoding a Hamming code word without error (e <7> = <0000000>).
Let at the receiving end of the channel received words # 7 → 60 and # 13 → 105 from table K,
u <7> + e <7> = <0 1 1 1 1 0 0> + <0 0 0 0 0 0 0>,
where there is no error, that is, it has the form e <7> = <0 0 0 0 0 0 0>.

As a result, the calculated syndrome has a zero value, which confirms the absence of an error in the words of the code.
Example 3 . Detection of one error in a word received at the receiving end of the channel (Table K).
A) Suppose it is required to transmit the 7th codeword, i.e.
u <7> = <0 1 1 1 1 0 0> and in one third from the left of the word, an error was made. Then it is summed mod2 with the 7th code word transmitted over the communication channel
u <7> + <7> = <0 1 1 1 1 0 0> + <0 0 1 0 0 0 0> = <0 1 0 1 1 0 0>,
where the error has the form e <7> = <0 0 1 0 0 0 0>.
Establishing the fact of the distortion of the codeword is performed by multiplying the obtained distorted word by the check matrix of the code. The result of this multiplication will be a vectorcalled codeword syndrome.
Let's perform such a multiplication for our original (7th vector with an error) data.

As a result of such multiplication at the receiving end of the channel, we obtained a vector syndrome S <nk>, the dimension of which is (n – k). If the syndrome S <3> = <0,0,0> is zero, then it is concluded that the word received on the receiving side belongs to the C code and is transmitted without distortion. If the syndrome is not equal to zero S <3> ≠ <0,0,0>, then its value indicates the presence of an error and its place in the word. The distorted bit corresponds to the number of the column position of the matrix H [nk, n], which coincides with the syndrome. After that, the distorted bit is corrected, and the received word is processed by the decoder further. In practice, a syndrome is immediately calculated for each accepted word, and if there is an error, it is automatically eliminated.
So, during the calculations, the syndrome S = <110> is the same for both words. We look at the check matrix and find the column that matches the syndrome. This is the third column from the left. Therefore, the error was made in the third digit from the left, which coincides with the conditions of the example. This third bit is reversed and we returned the words received by the decoder to the form of code words. The error was found and fixed.
That's all, this is how the classical (7, 4) Hamming code works and works.
Numerous modifications and upgrades of this code are not considered here, since it is not they that are important, but those ideas and their implementations that radically changed the theory of coding, and as a result, communication systems, information exchange, automated control systems.
Conclusion
The paper considers the main provisions and tasks of information security, names the theories designed to solve these problems.
The task of protecting the information interaction of subjects and objects from environmental errors and from the actions of the intruder belongs to codology.
Considered in detail is the (7, 4) Hamming code, which marked the beginning of a new direction in coding theory - the synthesis of correcting codes.
The application of rigorous mathematical methods used in code synthesis is shown.
Examples are given to illustrate the efficiency of the code.
Literature
Peterson W., Weldon E. Error-correcting codes: Trans. from English. M .: Mir, 1976, 594 p.
Bleihut R. Theory and practice of error control codes. Translated from English. M .: Mir, 1986, 576 p.