Comparing different methods of merging two sorted lists

Suppose we have two lists (of integers for simplicity), each sorted. We want to combine them into one list, which must also be sorted. This task is probably familiar to everyone; it is used, for example, in merge sort.

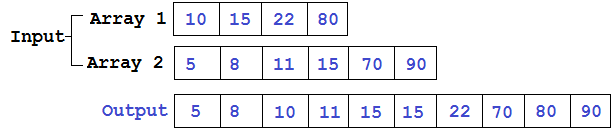
There are a lot of ways of implementation (especially in python). Let's take a look at some of them and compare the elapsed time for different inputs.

The main idea of ​​the algorithm is that by placing one label at the beginning of each list, we will compare the marked elements, take the smaller one and move the label in its list to the next number. When one of the lists ends, you need to add the rest of the second to the end.

Input data does not change

Let there be two lists list1and list2.

Let's start with the simplest algorithm: let us mark the labels for iand jand take the smaller one list1[i], list2[j]and increase its label by one until one of the labels goes beyond the boundary of the list.

In the first comparison, we will select the minimum element of the two minimum ones in our list and move to the next element, so the smallest element of the two lists will be at the zero position of the resulting one. Further, it is not difficult to prove by induction that the further merging will proceed correctly.

Let's move on to the code:

def simple_merge(list1, list2):
    i, j = 0, 0
    res = []
    while i < len(list1) and j < len(list2):
        if list1[i] < list2[j]:
            res.append(list1[i])
            i += 1
        else:
            res.append(list2[j])
            j += 1
    res += list1[i:]
    res += list2[j:] 
    #   list1[i:]  list2[j:]   ,     
    return res

Note that this code only uses forward movement in the list. Therefore, it will be enough to work with iterators. Let's rewrite the algorithm using iterators.

We will also change the processing of the ends of lists, since now we cannot copy to the end at once. We will process the elements until both iterators reach the end, while if one is already at the end, we will simply take from the second.

def iter_merge(list1, list2):
    result, it1, it2 = [], iter(list1), iter(list2)
    el1 = next(it1, None)
    el2 = next(it2, None)
    while el1 is not None or el2 is not None:
        if el1 is None or (el2 is not None and el2 < el1):
            result.append(el2)
            el2 = next(it2, None)
        else:
            result.append(el1)
            el1 = next(it1, None)
    return result

(result.append()) , . , , .

def gen_merge_inner(it1, it2):
    el1 = next(it1, None)
    el2 = next(it2, None)
    while el1 is not None or el2 is not None:
        if el1 is None or (el2 is not None and el2 < el1):
            yield el2
            el2 = next(it2, None)
        else:
            yield el1
            el1 = next(it1, None)

def gen_merge(list1, list2):
    return list(gen_merge_inner(iter(list1), iter(list2))) #    

python .

• merge heapq. , , , : , , .

  
  
  

  :

  
  
  

  from heapq import merge
  
  def heapq_merge(list1, list2):
  return list(merge(list1, list2)) #   

  
  
  

• Counter collections. Counter , , , , (, ).

  
  
  

  gen_merge_inner Counter(list1) Counter(list2):

  
  
  

  def counter_merge(list1, list2):
  return list(gen_merge_inner(Counter(list1).elements(), Counter(list2).elements()))

  
  
  

• , , . .

  
  
  

  def sort_merge(list1, list2):
  return sorted(list1 + list2)

  
  
  

, ( ). . pop(0) , .

def pop_merge(list1, list2):
    result = []
    while list1 and list2:
        result.append((list1 if list1[0] < list2[0] else list2).pop(0))
    return result + list1 + list2

4 , . , , . , . , , .

def reverse_pop_merge(list1, list2):
    result = []
    while list1 and list2:
        result.append((list1 if list1[-1] > list2[-1] else list2).pop(-1))
    return (result + list1[-1::-1] + list2[-1::-1])[-1::-1]

.

, :

• simple_merge
• iter_merge
• gen_merge
• heapq_merge
• counter_merge
• sort_merge
• pop_merge
• reverse_pop_merge

timeit. .

: , , , , . .

, $$$1$ $$$10^5$, $$$1$ $$$10^6$.

pop reverse_pop:

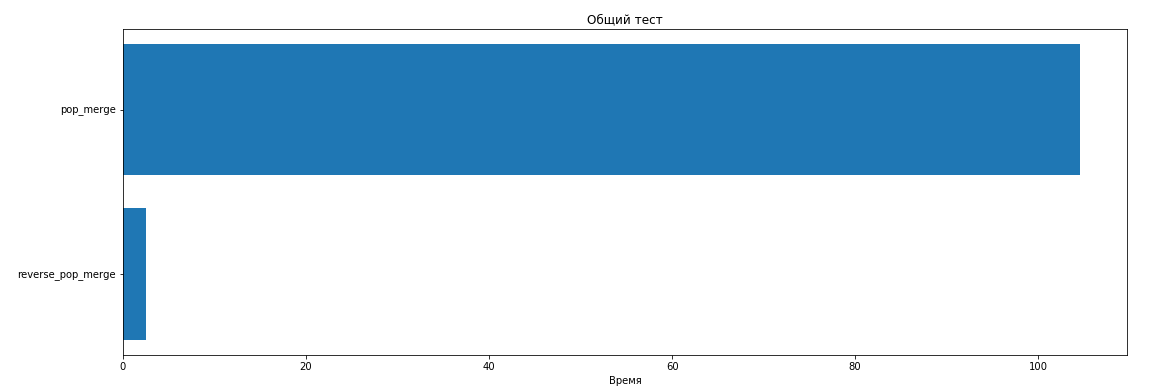
pop_merge , .

pop_merge, :

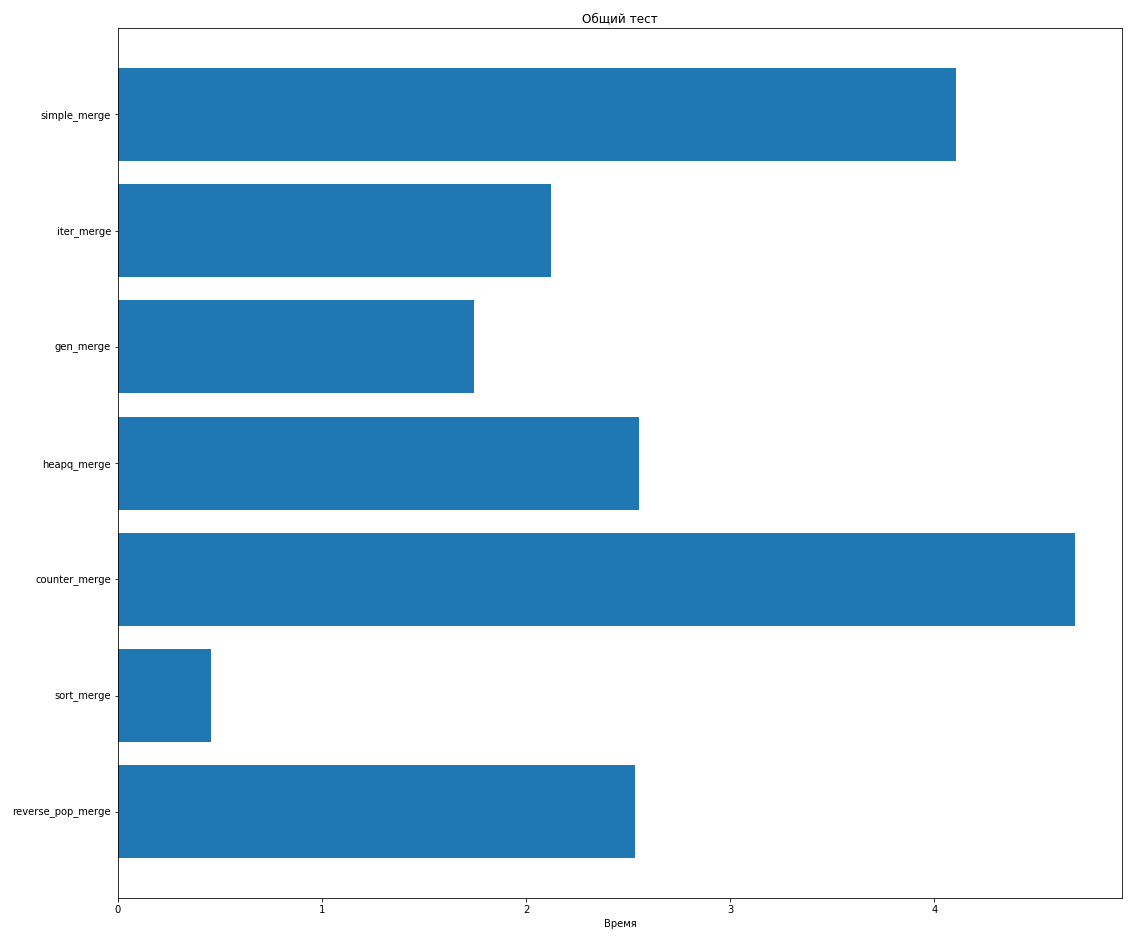
reverse_pop_merge heapq_merge.

, , , .

,

$$$[50x, 50(x+1))$, $$$x$ , $$$1$. $$$50$.

pop_merge heapq_merge, .

, ,

$$$x$, $$$10^4 + 100x$.

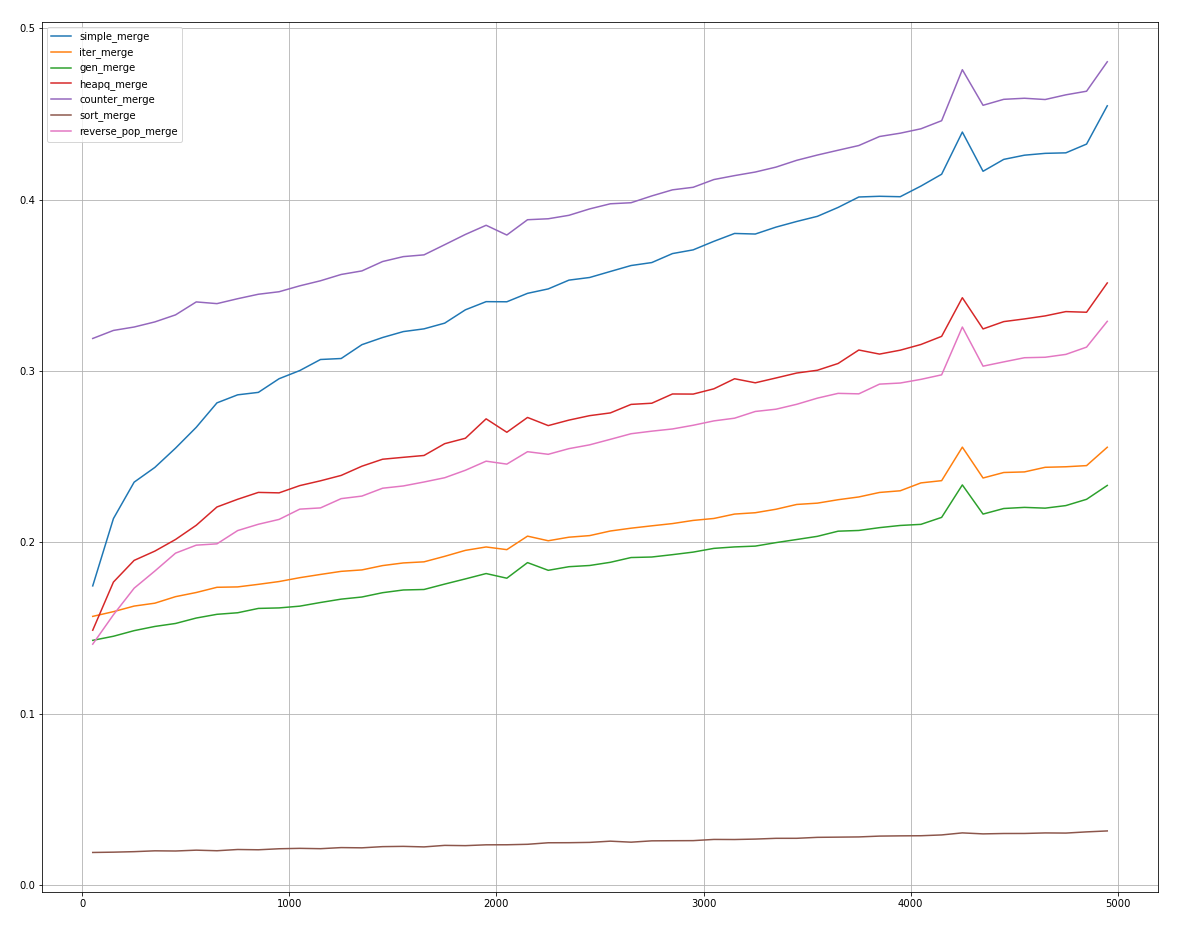
( ) reverse_pop_merge , sort_merge, .

,

, $$$5$, $$$1$.

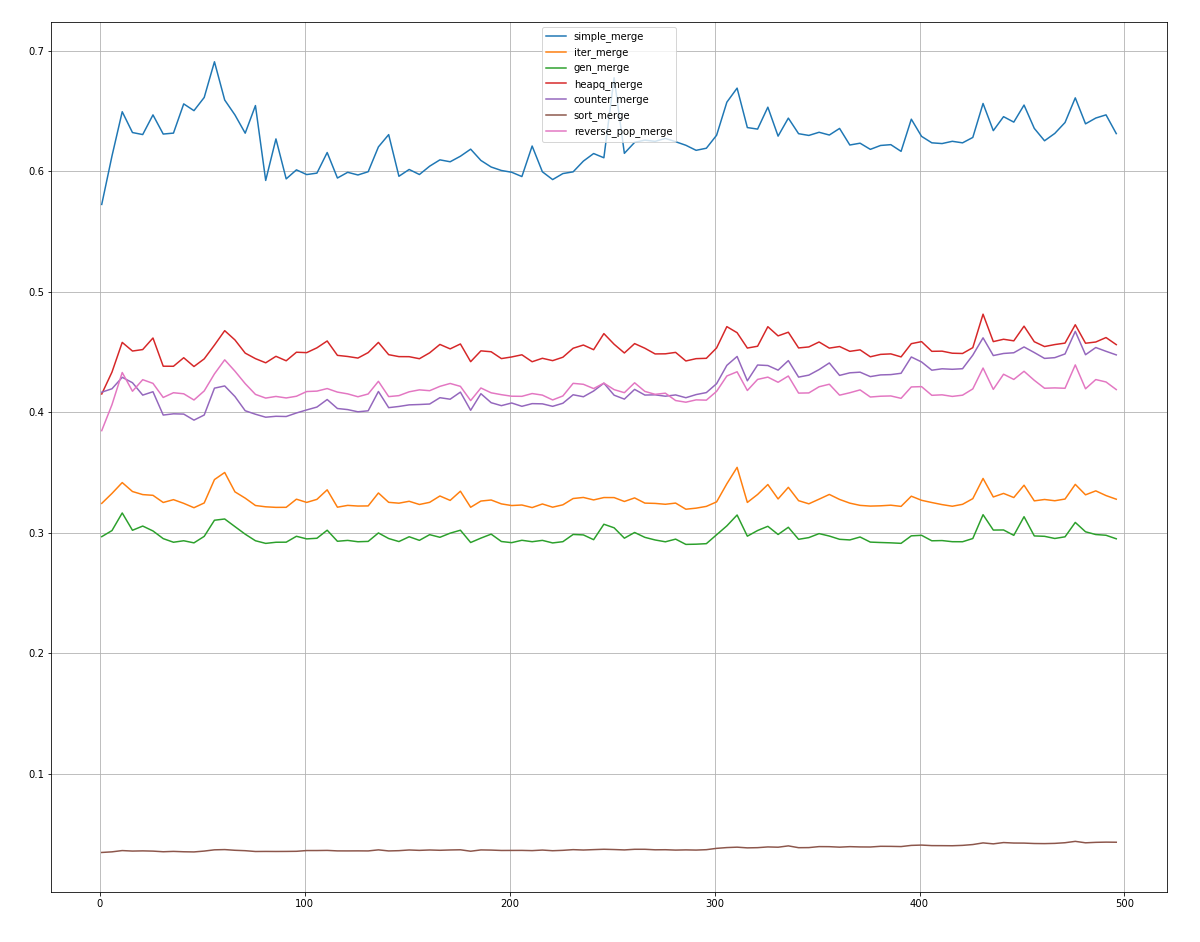
, counter_merge reverse_pop_merge heapq_merge, .

sort_merge! , .

In second place in the majority of cases there is gen_merge, it should be him iter_merge.

The rest of the methods use even more time, but some, in some extreme cases, achieve results of 2-3 places.

PS

Code, tests, jupyter notebook with graphs can be found on gitlab .

Perhaps this analysis is incomplete, I will be glad to add your options to the comparison, suggest.