These tools are not as close to the common man as, for example, a bank deposit, but they are important for modern financial markets. And they are periodically discussed in non-specialized media, and I think it is useful to get a general idea of options and how financial companies work with them.

In addition, this topic is associated with interesting mathematics, computational methods and the development of software systems - everything we love.
This post is an extended version of my video lecture “ Options. Basic parameters and examples of use ”as part of the Finmath for Fintech course.
So let's start with a few simple definitions. As elsewhere, there is its own "bird language", with which we will get to know a little.
What is an option?
Options are a class of financial derivatives. The term "derivative" means that the payment under such a contract depends on the price of some underlying asset.
The name seems to hint that such a tool provides some kind of optionality, that is, the ability to choose. But since there are two participants in the transaction, one of them gets an opportunity, and the other, on the contrary, assumes the obligation that he will provide such a choice.
Vanilla flavor
There are quite a number of different options contract options. There is simpler, there is more complicated, with bells and whistles, there are even more complex.
In English, simple options are called plain vanilla option (simple vanilla option). According to the internet, this is because the simplest and cheapest ice cream in the American stand was vanilla .
And the most vanilla-vanilla option is the European option.
European option
A European option is a contract under which the buyer of the contract receives the right, but not the obligation, to buy or sell an underlying asset at a predetermined price at a specified future time in the contract.
The underlying asset can be a stock or a currency rate. An option on a currency rate is called an FX option, it gives the right to exchange one currency for another at a pre-fixed rate. The market rate for the underlying asset is called the spot and is denoted as S t in the formulas .
An option that gives the right to buy the underlying asset is called a call option. The right to sell is a put option(put option). The price at which the option gives the right to conclude a deal in the future is called a strike , denoted...
The time specified in the contract in advance at which the option can be used is the expiry date of the option -...
Why is this needed?
Option as insurance
A contract that looks like an option and is familiar to everyone is insurance. Anyone who buys insurance gets the right, under certain conditions, to receive an insurance premium, and the insurance company undertakes to pay this premium. And here are a couple of examples.
Business Kolya
Kolya is the owner of a jigsaw business. Everyone needs a good jig, so Kolya is doing well. He entered the international market and sells jigs abroad. For example, production is located in a country where the XXX currency, widely known in the academic literature, is used, and jigs are sold abroad to a country where another well-known currency is used - YYY.
Planning and managing a highly competitive jigsaw business takes Kolya a lot of time and effort. And then there is a new problem - the changing exchange rate of YYY to XXX. This exchange rate is denoted XXXYYY.
Kolya knows the business well and can quite accurately say that in six months he will have a profit of 1 to 3 million YYY. They will need to be converted into XXX currency in order to pay salaries, rent, taxes and something to invest in business development. What if during this time the XXXYYY rate goes up? Kolya is confident enough that he will definitely need to convert one million, so that he can conclude a forward contract for one million XXXYYY. But there are two million more that he is not so sure of. Therefore, Kolya buys a call option on the XXXYYY currency pair.
Kolya bought a call option and will receive a payment at the time of expiration:
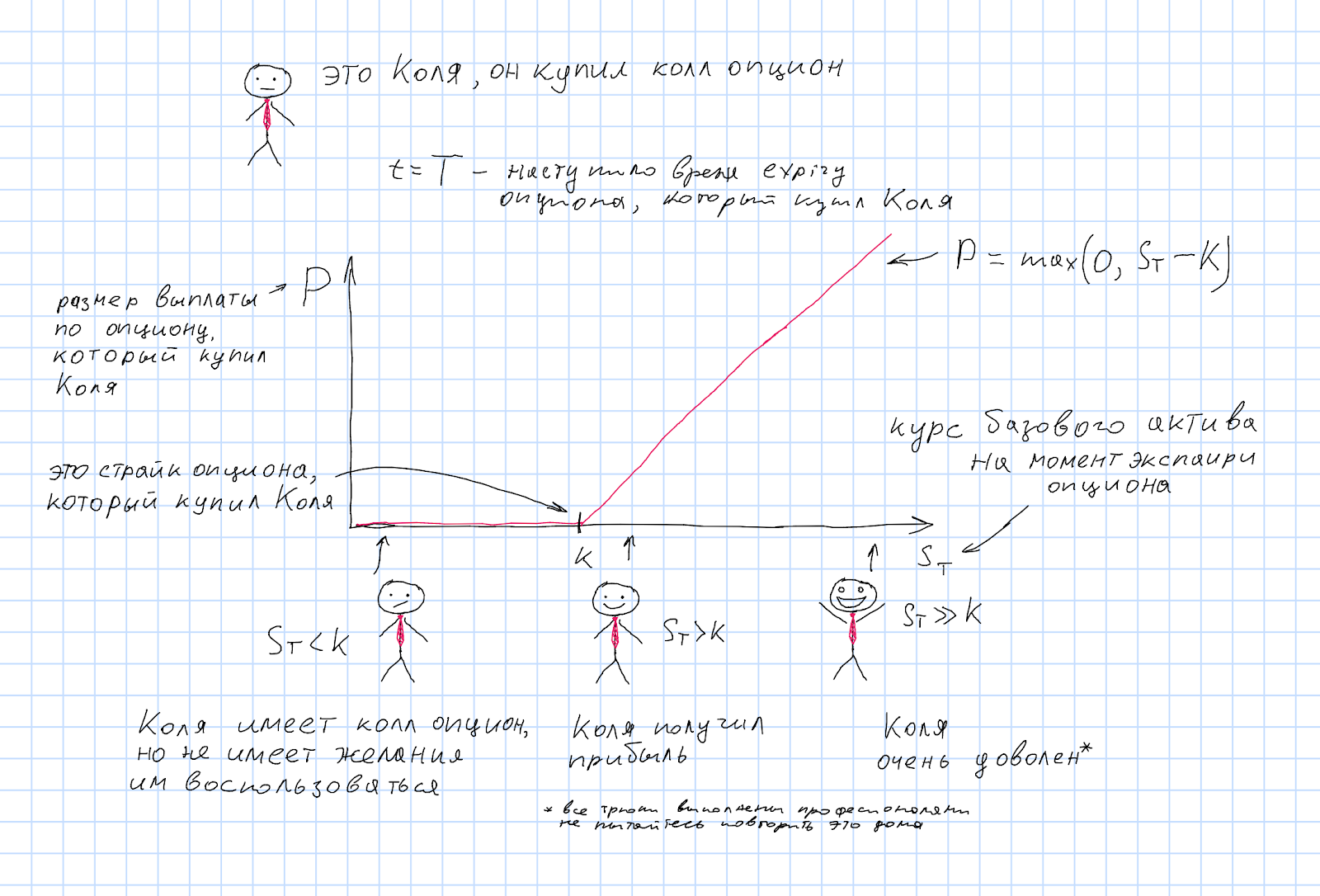
If at the time of expiration of the option the market exchange rate S T turned out to be less than the strike, i.e. S T <K, then it is unprofitable to use Kolya's option, it is cheaper to simply exchange currency at the current rate. The option does not impose any obligations on Kolya in this case. By analogy with insurance - “insured event” did not occur.
But if the currency rate goes up, then Kolya will definitely want to change the currency at the rate equal to the option strike, which in this case will be more profitable than the market one.
The speculator Petit's strategy
Options are also used in various stock trading strategies.
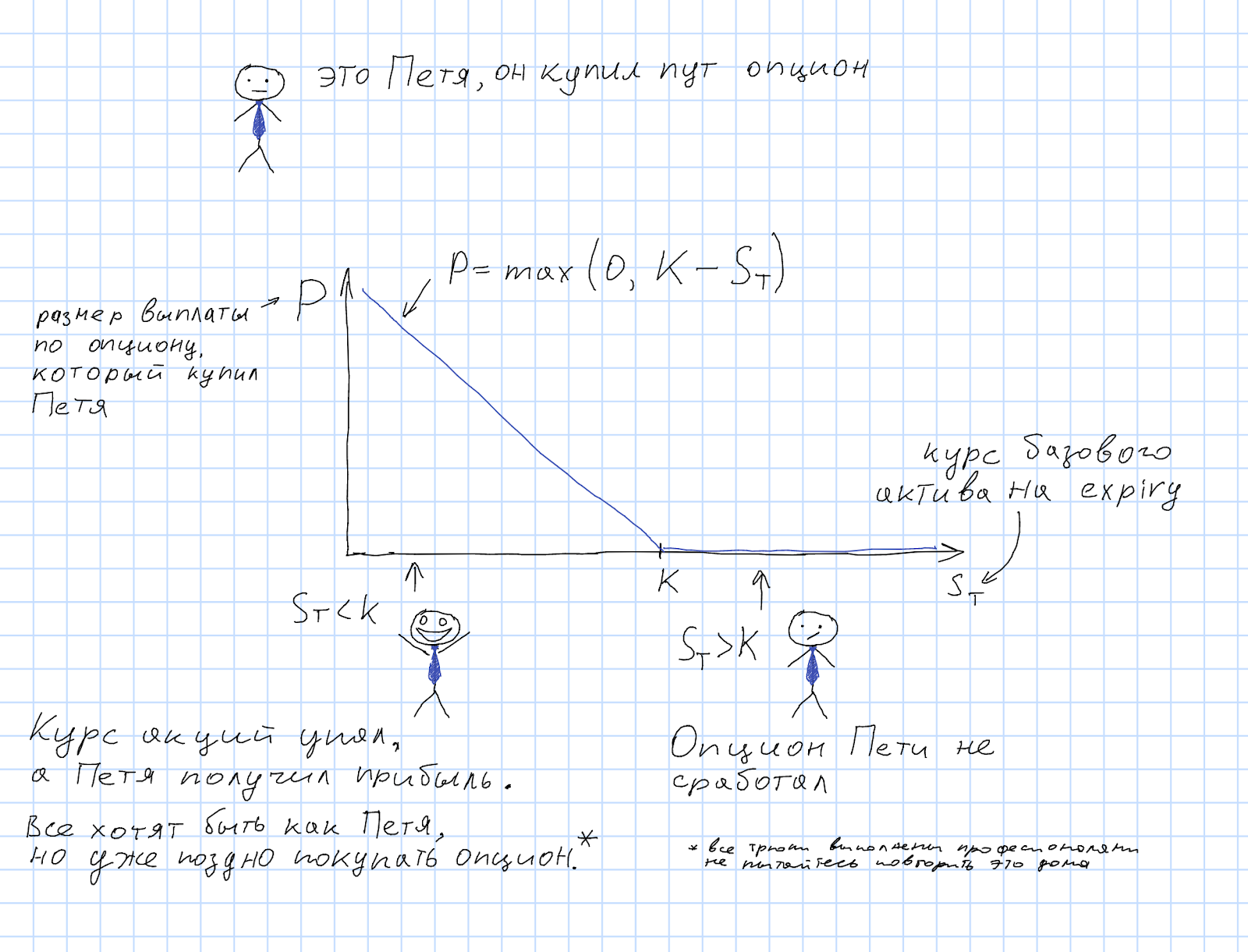
Petya is a stock speculator, and he has a super-ML-AI-cristal-ball-algorithm that predicts that in a month the shares of a certain company XYZ will plummet in price. Therefore, Petya buys a put option on XYZ shares. Those. the right to sell a share at the rate(option strike).
If the stock price at the time of the option expiration (S T ) really turned out to be below the strike, then Petya can buy a share on the market at a lower price and sell this share using the right that the option gives him. Thus, Petya will make a profit:...
But if the stock price still goes the other way and turns out to be more than the option strike, then Petit's option gives nothing, and the option payout is zero.
Petya bought a put option and will receive the payment at the time the option is exercised:...
These examples do not mean that a put option is only for speculators, and a call option is for hedging risks. If Petit's model predicted an increase in the rate, then he would need a call option, and if Kolya's business developed in such a way that he needed to plan a currency exchange in the other direction, then the choice would be with a put option.
It can be seen that the practical use of options in speculative strategies at the rate of the underlying asset requires only correctly guessing which inequalities will be true for prices in the future. It's not that hard (kidding). The same applies to the use of combinations of vanilla options, which will be discussed below.
In-the-money option and out-of-the-money option
When the exchange rate of the underlying asset is such that the option payout is zero, the option is said to have ended out-of-the-money (OTM) . For a call option this means S T <K, for a put option - S T > K.
If the rate is on the other side of the strike, then they say that the option is in-the-money (ITM) . The case of equality S T = K is called at-the-money (ATM) .
At the time of the conclusion of the option contract, no one knows what the price of the underlying asset will be at the time the option is exercised. But everyone knows the current price of the asset. If we apply the discount rules to the current price, then you can calculate the fair price of the forward contract for this underlying asset with a delivery time equal to the expiration time of the option. This is called the at-the-money forward (ATMF) . Knowing this price, it is possible to divide options that have not expired yet into ITM and OTM, depending on the option strike.
For strikes less than ATMF, call options will be in-the-money and put options will be out-of-the-money. For strikes larger than ATMF, the opposite will be true.
Formally, you can define both call and put options for any strike, but in practice, at-the-money-forward and out-of-the-money options will be liquid. After all, if the option strike is deep in the in-the-money zone, then the probability that the option will be exercised is estimated by the market to be close to one, and the price of such a contract is determined more by discounting than by the optionality of the option specified by the strike. Sometimes it is possible to trade ITM options, but only if their strike is close enough to the ATMF level.
Where did Kolya and Petya buy the option?
If an option is similar to insurance, then what "insurance companies" give Kolya and Petya the opportunity to buy such insurance? And how do they manage to fulfill their obligations under such contracts?
Fantastic Options and Where to Find Them
So where can you buy an option?
The answer, as is often the case, begins with the words "it depends ...". First of all, it depends on what underlying asset you want to buy an option on. The markets for stocks, exchange rates, interest rates, and commodity exchanges differ from each other. Naturally, trading options on different underlying assets has its own characteristics.
Stock exchange
Let's start with stock options. Stocks are usually bought and sold on the exchange. For an option contract, this is convenient because there is a good source of stock prices, incl. it is easy to determine the value of the option at the time of the experiment. This rate, in terms of the option, is the spot rate. You can even use a popular stock index, such as the S & P500 , as a spot rate for an option .
Stock trading is such a successful idea that stock options are also traded on the stock exchange. For example, at the Chicago Board Options Exchange . In order to organize trading in options on the exchange, you need to standardize options parameters. For a vanilla option, these are: the underlying asset, the strike and the expairi.
At the same time, in order for the option trading with the given parameters on the stock exchange to make sense, it is necessary that this option option be sufficiently liquid, i.e. there would be a sufficient number of people willing to buy and sell for him.
Non-exchange
Not everyone and not always have enough of the options that can be bought on the exchange. What to do? Buy or sell off the stock exchange! Such trades are called over-the-counter (OTC). In principle, this can be a transaction between any market participants. But where OTC markets arise, there is someone who specializes in providing quotes (and thus the ability to buy / sell) - market makers. With the development of computers and digital communication channels, OTC markets have changed a lot. Previously, for such a transaction, it was necessary to call a market maker or intermediary by phone. Now everything can be done through specialized programs. There are software interfaces for receiving quotes and executing transactions for use in trading robots. There are aggregators in active markets,which will automatically find the best buy and sell offer for a given contract automatically by polling different market makers. In many ways, at least from the point of view of liquidity, availability of current quotes and the convenience of making a deal, this is no longer very different from trading on an exchange.
An example of a successful OTC market is the currency market, the FX market. And options on it are also actively traded.
The advantage of the OTC market is that there is no need to introduce standards for contracts that can be traded. Therefore, the market maker can provide customers with the opportunity to request a price for any contract for which the market maker is able to calculate the price.
For vanilla options, this means arbitrary strike and expiry values. But this is just the beginning. Besides vanilla options, there are many different options options. Anything that is not a vanilla option is called an exotic option, or in short - an exotic.
I will tell you about some exotics below. Now it is important to note that each type of exotic options also has other parameters that vanilla options do not have, and the problem of standardizing contracts for exchange trading becomes even more acute. After all, exchange trading makes sense only for fairly liquid contracts, on the exchange you can only buy what someone else wants to sell. So exotic options are only traded on the OTC market.
Derivatives for derivatives
On the financial markets, not only spot transactions are actively traded, but also all kinds of derivatives. Futures, swaps, etc. And yes, there are options on them.
For example, stock prices for oil and other commodities are prices for futures. Accordingly, an oil option is an option on a futures.
Options on currency futures are also traded on exchanges, for example, on the Chicago Mercantile Exchange (CME).
If you already have a question: "Is there an option on an option?", Then the answer is: yes, there are... If there is a potential demand for some option and the market maker has the ability to take on such obligations, i.e. understanding how to calculate the price and how to then manage the risks (hedge) such a contract, the market will sooner or later respond to such demand with supply.
The more different products a market maker has to offer, the more different customers he can attract. You also need to understand that in the options market, as in any other market for financial products, there are buy and sell prices, the difference between them is called the spread, and this is the main source of the market maker's income. Naturally, the spread is narrower for more liquid products, and wider for less liquid products.
But let's go back to vanilla options and look at examples of products made up of them.
Vanilla strategies
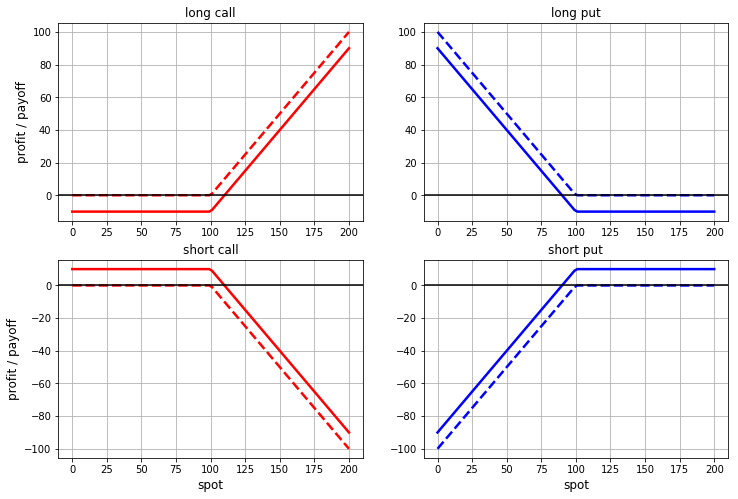
We know what the payout schedule for call and put options looks like, but there are a couple of obvious things to mention. First, options can be bought or sold. In financial market jargon, they say that we are a long option if we bought an option, and that we are a short option if we sold an option. The payout on a short position in an option is equal to the payout on a long position with the opposite sign.
Secondly, in order to buy an option (take a long position), you need to pay a premium, and the party that assumes obligations on the option (short position) receives a premium for this. Incl. it makes sense to count not only the option payment, but also the total profit including the premium.
We get four options. The dashed lines show the graphs of the payout functions (excluding the premium), and the solid lines show the profit / loss function with the premium:
The next simple idea is that options can be bought and sold not one at a time, but in combinations. Some combinations are so popular and so important to the market that they have established names.
Balance combination: Straddle
The first combination on our list is straddle. It turns out if you add up call and put options with the same strike. ATM straddle is especially popular, i.e. both options have a strike equal to the at-the-money forward.
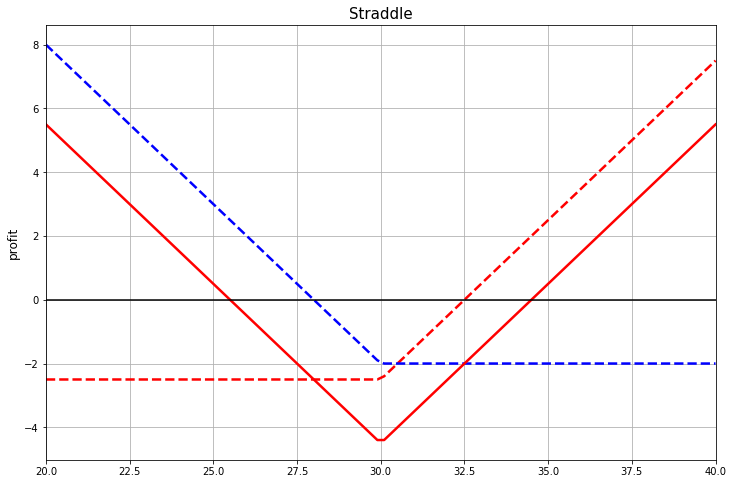
In this picture, the dotted line shows the profit for individual options (including the premium). And the solid line is their sum, i.e. profit for the entire structure as a whole, naturally, also taking into account the premium
If you look at the straddle as a speculative strategy based on the price of the underlying asset, then if you buy a straddle, you will make a profit if the price level of the underlying asset goes far enough from the at-the-money level, and it doesn't matter which way.
If you have already heard something about options and you know what an option delta is, then you can clarify that for some underlying assets they prefer to use not an ATMF straddle, but a deltoneutral (DN) straddle. Those. the strike is chosen so that the delta of the put and call options in total gives zero.
Association Game: Strangle
Take a look at this picture. What associations do you have?
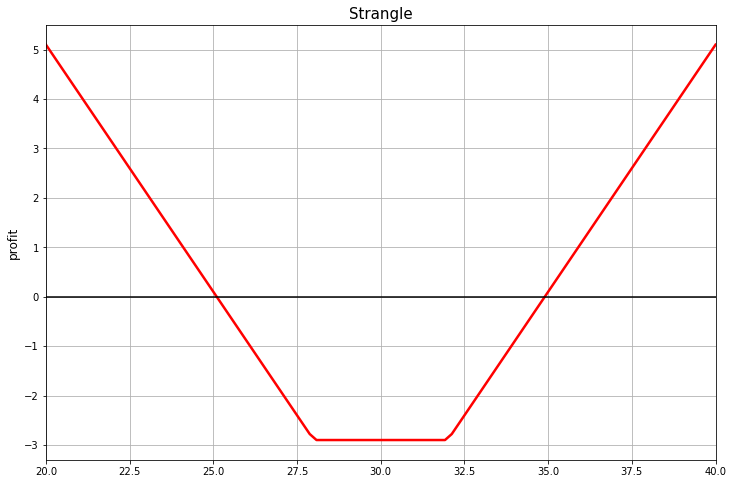
The common name for a combination of vanilla options with this payout is strangle.
The English Explanatory Dictionary says strangle is "to kill someone by pressing their throat so that they cannot breathe." Those. it is about strangulation. Why such a brutal name appeared for such a payout function, I do not know. Apparently, this is how the Wall Street Option Traders Association worked in the early 20th century. On the other hand, it could have been worse. You could call it "the chainsaw massacre," for example.
From the point of view of option strategies, strangle is a put + call, with different strikes. It looks like a straddle, but due to the fact that options strikes are in the OTM zone in this combination, these options are cheaper than ATMF options. Consequently, the whole combination will be cheaper than ATMF straddle.
For a speculator, strangle has about the same meaning as straddle, with the difference that strangle is cheaper, but in order to make a profit, it is necessary for the rate to move more away from the ATM level.

Risk Reversal
The next combination is risk reversal. Buy an OTM call option and sell an OTM put option.
From the point of view of a speculative strategy, this is a rather aggressive bet that the rate of the underlying asset will go up. Because If we sell a put option and get a premium for it, then the cost of such a rate will be lower, but if the rate goes down, our problems will be greater.

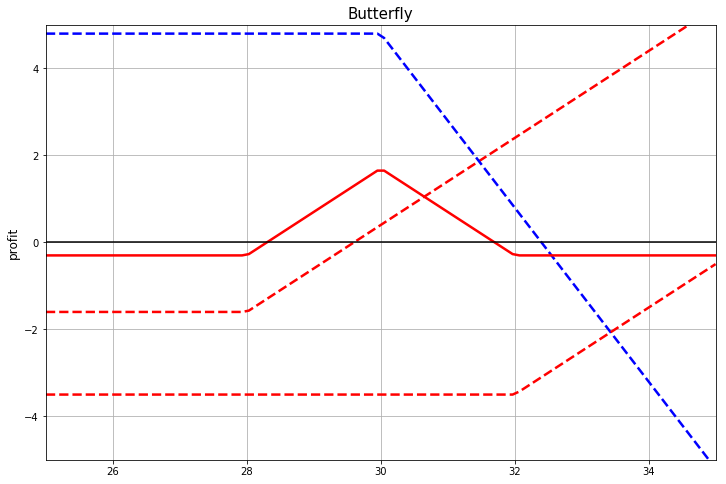
Butterfly
Two options are not enough to construct a payout in a structure called a butterfly. In the figure below, this combination is replicated using call options as follows: buy options with strikes 28 and 32 with par 1 and sell an option with strike 30 and par 2.
The same payout can be constructed by buying strangle and selling straddle. And this is what is usually done in practice.
The replication of this payout only through call options, as in the figure, is interesting as follows. Let's denote the central strike in the structure by, and the difference between this strike and the other two is like ... Then the price of such a structure will be... As such, it looks like a difference scheme for calculating the second derivative. Of course, for this you need to striveto zero, and such data cannot be obtained directly from market quotes, but in some cases, it is possible to get a good approximation for those quotes that are available. Or at least a meaningful numerical estimate of the convexity of a function.
Sometimes this property is convenient for theoretical analysis. In the books you can see reasoning where infinitely small "butterflies" are considered. Those. butterfly structure, in which the difference between strikes tends to zero.
On this site you can experiment with the options for these and some other combinations of vanilla options.
Experimental barriers
Let's go back to the payout function for one option. For example, let's take an ATMF call option. For the person who purchased it, this contract, as it were, fixes the future rate of the asset at the time the option is exercised, if the rate turns out to be higher than the ATMF level. ATMF-level is some current estimate of the "fair" rate at the time of the experiment, but, of course, the real value of this rate in the future is a random variable. Nobody knows exactly what will happen to the course. Still, we can say that one level of the course is more likely than another. And we can say that the probability of rate values that are far from ATMF is less than that of close ones.
But the usual call option works for all possible values of the rate above the strike. And this, by the way, is included in his prize. Is it possible not to pay for this if we estimate the probability of exceeding a certain level as zero?
If such an idea comes to mind, then it will not be superfluous to find out how much such a pay-off will cost (on the schedule, the payment excluding the premium):
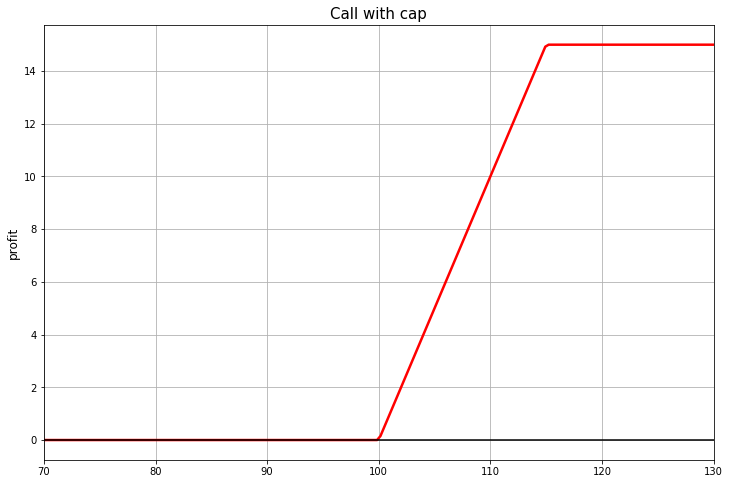
Or like this:

If the market maker's customers are interested in such products, then the market maker should be able to calculate prices for them.
The first payout function is easy to replicate with two call options. One option must be bought and the other sold.
The second pay-off is called a barrier option. In this case, the barrier acts only on the experience, a barrier with such a rule is sometimes called the European barrier. And the effect of the barrier in this case is that when the spot crosses the barrier, the option "knocks out". This is called the "knockout barrier".
There may be a knockin barrier. The owner of such an option will receive a payment only if the price of the asset on the expiry has gone far enough from the strike:

In this example, the option's strike is 100 and the KI barrier is 115.
Binary options
In order to replicate the payout with European barriers, simple vanilla options are not enough. You need options with the same espair rules as European options, but the payout function for which looks like a stepping stone.
Such options in Russian are called binary options. There are two names in English: binary option and digital option.

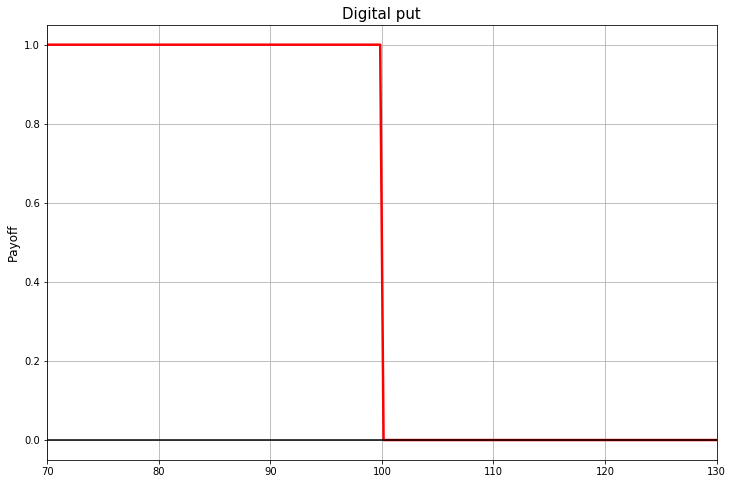
By themselves, binary options are a purely speculative instrument like a lottery ticket. If the rate is below the strike, the owner of the binary call option receives a fixed payment, if not, he receives nothing. But if they are part of an EKI or EKO pay-off, they can help to choose the parameters (and therefore the price) of insurance against the adverse movement of the underlying asset, more suitable for a particular case.
Vanilla vanilla strife
In addition to European options, there are also American options .
The difference is that the European option can only be exercised at the time of the experiment. And the American option is also at any time before.
Such geographical names are apparently connected with the fact that at some point one type of options was popular in European markets, another - in American ones. But today these are just established terms.
American options are often traded on exchanges. And in general, they are quite common. And they can also be categorized as vanilla options rather than exotic ones.
Continuous barriers
The most real exotic options are barrier options. In such options there is a barrier, but unlike European barriers, which are valid only for expiration, here we mean a barrier that is valid for the entire life of the option. Such barriers are called either continuous or American. If they talk about a barrier without specifying anything, then they usually mean just such barriers.
A continuous barrier can also be placed in the OTM region of the underlying asset rate relative to the option strike, which makes no sense for the European barrier. And in general, here the number of possible options increases. It is possible to define a barrier option with two barriers (upper and lower). You can make one barrier like knockout, and another like knockin ... There are many options, some more popular, some rare. They trade such exotic things, of course, on the OTC market.
In this type of exotic, it is important that its final payment depends not only on the price of the asset on the experience, but also on the entire path that the random process of the underlying asset price has passed from the moment the contract is concluded to the experience.
Asian options
Another typical example of an option, the price of which depends not only on the value reached by the spot on the espairi, but also on the entire path, or at least on the prices realized at some predetermined points along the path. The Asian option uses an average of such intermediate values. For example, it can be done like this: to determine the payout according to the call option rule, the average value is taken, not the spot value on the experience. And the payout will be...
Such an option is less sensitive to short-term fluctuations in the underlying asset rate, which may accidentally occur at the time the option is exercised.
Options that depend on the spot path taken, such as Asian options and options with continuous barriers, usually require more complex models and more computationally expensive methods.
A little about modeling
So, now, in general terms, it is clear what contracts the options market participants have to deal with. Now we can say a few words about what tasks, for example, a market maker needs to solve in order for his activities in the market to be successful.
Pricing
On the stock exchange or OTC market, you can get prices for liquid call and put options for different expires and different strikes. It will be some number of points with parameters... But you need to be able to work not only with these options, but also with other strikes, other experiences and exotic options. For this, models are built based on the results of non-school probability theory (stochastic differential equations, martingale measure, etc.).
If you look at what these models do from a bird's eye view, then they answer questions like "how to calculate the price for a vanilla option, for which the market has no quotas, based on the prices that are available?" or "how, having this data on the prices of liquid vanilla options, to calculate the prices of more complex contracts - binary, or with continuous barriers, or any other exotic?"
It turns out to be convenient, or at least generally accepted, to talk about a certain characteristic that is associated with the probabilities of realizing different possible values of the underlying asset rate and is a function of parameters ... This characteristic is called “implied volatility”. Because it is a function of two parameters, then one speaks of a volatility surface. If expairi is fixed, then it is a function of one variable, and then they talk about the “smile” of volatility.
From the perspective of option traders, options trading is volatility trading. And speculative strategies using one or more vanilla options can be aimed specifically at speculating with volatility.
"Trading abstract volatility in a vacuum"
Usually for those calculations that need to be done, there is no analytical solution and you need to use computational methods. Typical computational methods that are used are the numerical solution of partial differential equations and the Monte Carlo method.
Position Management: Dynamic Hedging
Mathematical models and computational methods help to calculate the prices of different options in accordance with other prices for more liquid instruments. But this is only one side of the problem. Prices reflect current market expectations. These expectations are changing, and no one knows what will be realized in the future.
Clients come to the market maker and want to conclude a deal with him: someone in order to get insurance, someone in order to implement some kind of speculative strategy. Which deals and when will be requested - the client chooses. The market maker must be prepared to commit to the appropriate option obligations. To do this, he needs some kind of algorithm of actions, how to fulfill these obligations. Some kind of technology that would help him replicate the payment of an option, regardless of what happens in the market. Sounds too good to be true? This is partly true, but, nevertheless, there is technology that comes surprisingly close to this.
The technology is called dynamic hedging. The bottom line is that some risk indicators for our position are considered and periodically we buy some instruments on the market that compensate for these risks. A typical example of such risk is delta, the partial derivative of the price of the derivative at the rate of the underlying asset. In order to compensate for the delta, you just need to buy the underlying asset in an amount equal to the delta and with the opposite sign. What short selling can mean. A strategy based on delta hedging is called (surprise!) Delta hedging .
Within the framework of mathematical models, which are usually built on assumptions that are usually not fulfilled in practice, it can be shown that delta hedging can mathematically accurately replicate the payout of an option. In this case, it is only necessary, in addition to all the simplifications and assumptions inherent in the model, to direct the period between portfolio rebalancing to zero. This is how option replication works using delta hedging in the famous Black-Scholes model.
Despite the fact that rigorous mathematical proofs require neglecting many things that are important in practice, the very idea of dynamic hedging turns out to be surprisingly resistant to the fact that many of these assumptions are not fulfilled in practice. This is what allows the market maker to engage in his activities, significantly reducing the risk that he takes on at the same time.
Here, the market maker does not hurt to have a large client base with multidirectional interests. Of course, the way a market maker finds a buy and sell quote for volatility is conceptually similar to how a market maker finds that quote in the spot market . The difference is that for each asset you need to find more than two prices, and the buy and sell quotas for the imputed volatility for those strike and expiry values that are considered reasonable in the market. This usually means that you need to at least have these buy and sell quotas for several fiducials and calibrate the model parameters so that the model matches them.
The points to which the model needs to be calibrated can be specified in different ways. In the FX options market, the pivot points are straddle, risk reversal and butterfly quotes.
Volatility speculation
As already mentioned, for an option trader, options trading is volatility trading. This applies to speculative strategies too. The strategy can be based not on predicting what the price of the underlying asset (spot) will turn out to be on the experience, but on the fact that volatility is underestimated or overestimated by the market. Based on this, you can decide whether to buy or sell an ATMF straddle. Or if the slope of the volatility "smile" is estimated incorrectly, then you can decide whether to buy or sell risk reversal. Etc. As usual with speculative strategies, you just need to guess where the market went wrong and what will happen in the future.
All articles in this series
- Value of money, types of interest, discounting and forward rates. Educational program for a geek, part 1
- Bonds: coupon and zero coupon, yield calculation. Educational program for a geek, part 2
- : . , . 3
- . , . , . 4
- . , . 5
- . , . 6
- : - , . , . 7