🎛️ 🤬 🚴🏿 Markov and Python chains - understanding the theory and assembling a text generator 😩 📑 ☠️

We understand and create

The good news before the article: high math skills are not required to read and (hopefully!) Understanding.

Disclaimer: The code part of this article, like the previous one , is an adapted, supplemented and tested translation. I am grateful to the author, because this is one of my first experiences in the code, after which I flooded even more. I hope my adaptation will work the same for you!

So let's go!

The structure is like this:

What is a Markov chain?
An example of how the chain works
Transition matrix
Markov chain model with Python - data-driven text generation

What is a Markov chain?

Markov chain is a tool from the theory of random processes, consisting of a sequence of n number of states. In this case, connections between nodes (values) of the chain are created only if the states are strictly next to each other.

Keeping in mind the fat-type word only , let us deduce the property of the Markov chain: The

probability of a certain new state in the chain depends only on the present state and does not mathematically take into account the experience of past states => A Markov chain is a chain without memory.

In other words, the new meaning always dances from the one that directly holds it by the handle.

An example of how the chain works

Like the author of the article from which the code implementation is borrowed, let's take a random sequence of words.

Start - artificial - fur coat - artificial - food - artificial - pasta - artificial - fur coat - artificial - end

Let's imagine that this is actually a great verse and our task is to copy the author's style. (But doing so is, of course, unethical)

How to decide?

The first obvious thing I want to do is to count the frequency of words (if we were to do this with a live text, first it would be worthwhile to normalize - to bring each word to a lemma (dictionary form)).

Start == 1

Artificial == 5

Fur coat == 2

Pasta == 1

Food == 1

End == 1

Keeping in mind that we have a Markov chain, we can plot the distribution of new words depending on the previous ones graphically:

Verbally:

the state of the fur coat, food and pasta 100% entails the state of artificial p = 1
the “artificial” state can lead to 4 conditions with equal probability, and the probability of coming to the state of an artificial fur coat is higher than to the other three
end state leads nowhere
the state "start" 100% entails the state "artificial"

It looks cool and logical, but the visual beauty doesn't end there! We can also construct a transition matrix, and on its basis we can appeal with the following mathematical justice:

What in Russian means “the sum of a series of probabilities for some event k, depending on i == the sum of all values of the probabilities of event k, depending on the occurrence of state i, where event k == m + 1, and event i == m (that is, event k always differs by one from i) ”.

But first, let's understand what a matrix is.

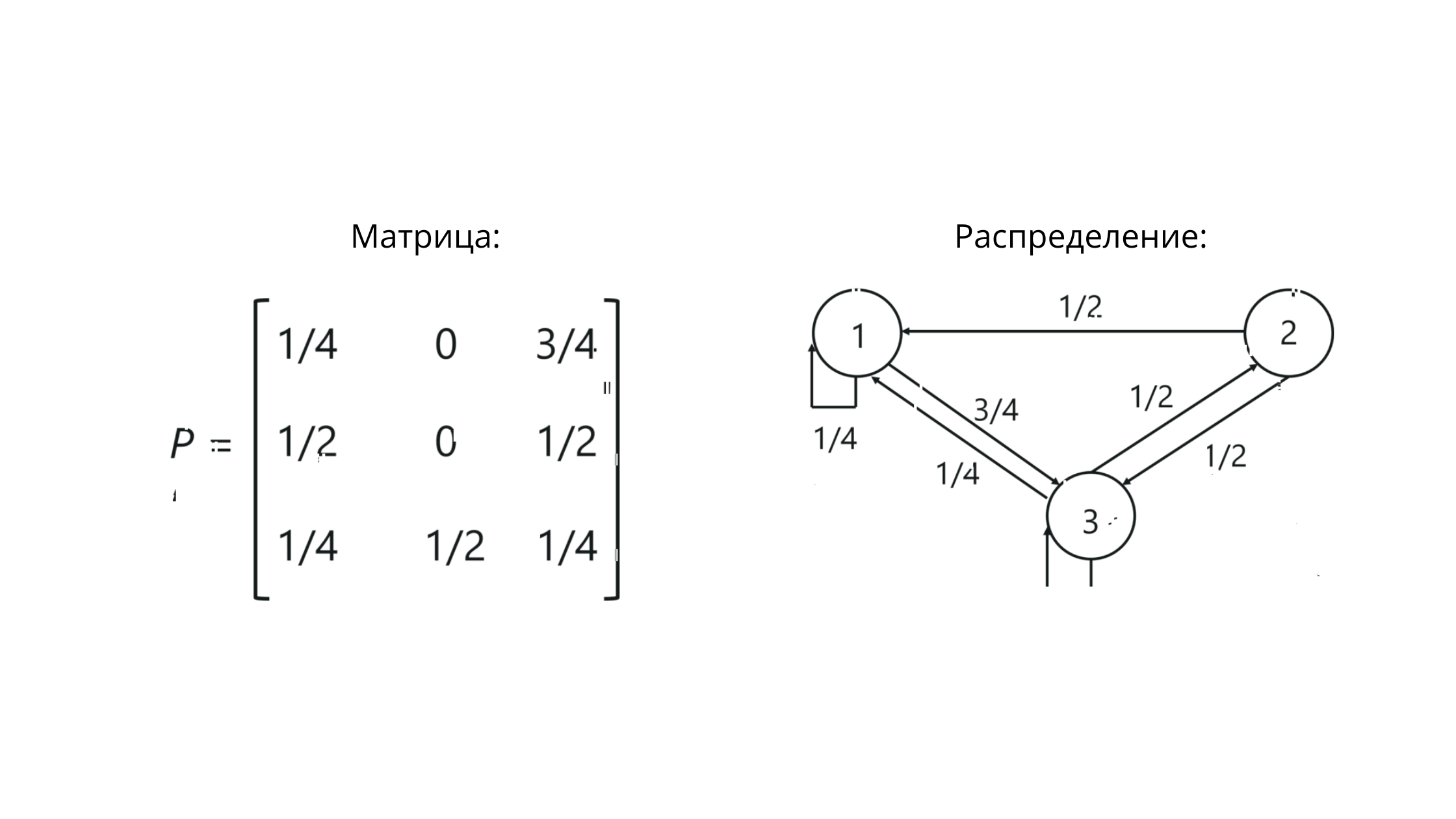
Transition matrix

When working with Markov chains, we are dealing with a stochastic transition matrix - a set of vectors, within which the values reflect the values of the probabilities between gradations.

Yes, yes, it sounds like it sounds.

But it doesn't look so scary:

P is the notation for a matrix. The values at the intersection of columns and rows here reflect the probabilities of transitions between states.

For our example, it will look something like this:

Note that the sum of the values in the row == 1. This means that we have built everything correctly, because the sum of the values in the row of the stochastic matrix must equal one.

Bare example without faux fur coats and pastes: An

even naked example is the identity matrix for:

the case when it is impossible to go from A back to B, and from B - back to A [1]
the case when the transition from A to B back is possible [2]

Respecto. With the theory finished.

We use Python.

A model based on the Markov chain using Python - generating text based on data

Step 1

Import the relevant package for work and get the data.

import numpy as np
data = open('/Users/sad__sabrina/Desktop/1.txt', encoding='utf8').read()

print(data)

     ,   ,        ,    ,     (   « memorylessness »).  ,     ,        ,          ,        ,   ,    ; ..,     ,       .

Don't focus on the structure of the text, but pay attention to the utf8 encoding. This is important for reading the data.

Step 2

Divide the data into words.

ind_words = data.split()
print(ind_words)

['\ufeff', '', '', '', '', ',', '', '', ',', '', '', '', '', '', '', '', ',', '', '', '', ',', '', '', '', '', '(', '', '', '«', 'memorylessness', '»).', '', ',', '', '', '', '', ',', '', '', '', '', '', '', '', ',', '', '', '', '', '', '', '', '', '', ',', '', '', '', '', '', '', '', ',', '', '', ',', '', '', '', ';', '..,', '', '', '', '', ',', '', '', '', '', '', '', '.']

Step 3

Let's create a function to link pairs of words.

def make_pairs(ind_words):
    for i in range(len(ind_words) - 1):
        yield (ind_words[i], ind_words[i + 1])
pair = make_pairs(ind_words)

The main nuance of the function in the use of the yield () operator. It helps us meet the Markov chaining criterion - the memoryless storage criterion. With yield, our function will create new pairs as it iterates (repetitions), rather than storing everything.

A misunderstanding may arise here, because one word can turn into different ones. We will solve this by creating a dictionary for our function.

Step 4

word_dict = {}
for word_1, word_2 in pair:
    if word_1 in word_dict.keys():
        word_dict[word_1].append(word_2)
    else:
        word_dict[word_1] = [word_2]

Here:

if we already have an entry about the first word in a pair in the dictionary, the function adds the next potential value to the list.
otherwise: a new entry is created.

Step 5

Let's randomly choose the first word and, to make the word truly random, set the while condition using the islower () string method, which satisfies True if the string contains lowercase letters, allowing the presence of numbers or symbols.

In this case, we will set the number of words to 20.

first_word = np.random.choice(ind_words)
 
while first_word.islower():
    chain = [first_word]
    n_words = 20
    first_word = np.random.choice(ind_words)
    
    for i in range(n_words):
        chain.append(np.random.choice(word_dict[chain[-1]]))

Step 6

Let's start our random thing!

print(' '.join(chain))
   ; ..,     ,     ,      (

The join () function is a function for working with strings. In parentheses, we have specified a separator for values in the line (space).

And the text ... well, it sounds machine-like and almost logical.

PS As you may have noticed, Markov chains are useful in linguistics, but their application goes beyond natural language processing. Here and here you can familiarize yourself with the use of chains in other tasks.

PPS If my code practice turned out to be incomprehensible to you, I am attaching the original article. Be sure to apply the code in practice - the feeling when it "ran and generated" is charging!

I am waiting for your opinions and I will be glad to have constructive comments on the article!

Markov and Python chains - understanding the theory and assembling a text generator

We understand and create

What is a Markov chain?

An example of how the chain works

How to decide?

Transition matrix

More articles: