Quantum computing and cryptology

The development of computer technology is moving in different directions, not being limited to the phenomena of classical physics, electronics, optics and now quantum mechanics.

Acquaintance with the problem of quantum cryptology and related ones close to it (not only in publications) showed that there are certain shortcomings and gaps in its description and presentation. Describing the specifics of a particular physical phenomenon, an object, the author ignores its environment, even the closest one that has a direct impact on the object (often a disturbing influence). This is not a reproach to the authors, their right to present as they do. It is rather my motive to join the general stream of consciousness. The material material side of quantum phenomena manifests itself in one way or another and ignoring it can have a significant negative effect. What is meant? Material implementation of quantum computers (QCs), registers, individual qubits - all of which QCs are made of. User exchange of the results obtained through communication networks and, finally, protection,the integrity and availability of such results from the intruder are also problems.

Quantum cryptology and related topics

A new direction of physics - quantum information - arose at the junction of quantum mechanics, optics, information theory and programming, discrete mathematics, laser physics, spectroscopy and includes questions of quantum communication systems, quantum computing, quantum computers, quantum teleportation and quantum cryptology, problems of decoherence and spectroscopy of single molecules and impurity centers.



Even without touching on cryptology, quantum physics relies on and uses such a large number of classical physical phenomena to describe its concepts and phenomena, which in school physics (and perhaps in university physics) have been "galloped" or even passed by that almost every concept (like familiar) requires explanation due to new discoveries and achievements of recent years, which is practically impossible to do within the framework of the article. But this selection of material is the problem of the author, not the reader.



In the theory of cryptology (cryptography + cryptographic analysis), several periods (stages) of development can also be distinguished. Ancient symmetric cryptology (single-key, both sides of the communication channel use the same key); asymmetric or two-key cryptology (a message is encrypted with a public key, and decrypted with another - with a private key). Finally,

the next stage in the development of cryptology covers the present and began with the realization of the possibility of building a quantum computer (QC) and quantum cryptology.



Experts in classical cryptology understood and recognized that such a computer is a powerful tool for the cryptographic analysis of ciphers, which in a matter of seconds will be able to break a classic cipher of any strength. But they saw the other (positive) side of the opening possibilities - the possibility of building quantum cryptography with practically unbreakable ciphers.



The idea of ​​quantum cryptography was born almost simultaneously with the idea of ​​using quantum objects for computations, that is, with the idea of ​​creating a quantum computer and a communication system using quantum channels along with traditional ones.

The quantum channel of the communication system and its elements

Today we already live in a world of quantum networks that stretch for thousands of kilometers and go out into space. The global market for commercial quantum communication systems is dominated by three companies: the Chinese Qasky and QuantumCTek, as well as the Swiss ID Quantique (since 2001). They supply virtually the entire spectrum of solutions and components, from single photon sources and detectors, quantum random number generators to integrated devices. In Russia, such a network connected two offices of Gazprombank in 2016, located at a distance of about 30 kilometers from each other. In the same year, the PRC launched the QUESS satellite - Quantum Experiments at Space Scale, which provided quantum distribution of keys at a distance of over 7600 km between the observatories in Beijing and Vienna.

Quantum communication channel scheme

Figure 1. Schematic diagram of a quantum channel and quantum key distribution protocol



The idea and implementation of quantum cryptography is illustrated in Figure 1. In the image on the left - the sending side of the message, on the right - the receiving side. Important necessary elements of the system are photomultipliers that act as photodetectors, Pockels (Pockel) cells, a calcite prism (Wollaston), and a polarizer. Of course, without the rest of the elements: a light-emitting diode based on a quantum dot (laser), lenses, collimator, optical fiber and photon flux, the system cannot be built, but these elements are well known, used for a long time and in many systems with completely different purposes. A quantum channel with satellites is implemented without optical fiber.



Let us make explanations for individual elements of the circuit.



Photon is an elementary particle, a quantum of electromagnetic radiation in the form of transverse electromagnetic waves and a carrier of electromagnetic interaction. It is a massless particle that can exist in a vacuum only moving at the speed of light. The photon's electric charge is also zero. A photon can be in only two spin states with a spin projection on the direction of motion (helicity) ± 1. Muon is the quantum of the muon field. Photon is a quantum of the electromagnetic field. In physics, photons are denoted by the letter γ.



Light emitting diode. In 2001, Andrew Shields and his colleagues at TREL and the University of Cambridge created a diode capable of emitting single photons. This made it possible to transmit polarized photons over long distances. The experimental demonstration was able to transmit encrypted data at a rate of 75 Kbps - while more than half of the photons were lost.



The Pockels cell (sometimes called the Pockel cell) is a crystal placed between two crossed nicols. Nicoli do not transmit light in the absence of an electric field, and when the field is applied, transmission appears. The external field (lines of force) can be perpendicular to the propagation of light (transverse modulator) or parallel (longitudinal modulator).



The Pockels effect (the effect is named after F. Pockels, who studied this phenomenon in 1893) is the phenomenon of a change in the refractive index of light in crystals (optical media) when exposed to a constant or alternating electric field. It differs from the Kerr effect in that it is linear in the field, while the Kerr effect is quadratic. The Pockels effect is observed only in crystals that do not have a center of symmetry: due to the linearity, when the direction of the field changes, the effect should change sign, which is impossible in centrally symmetric bodies.



The effect is clearly seen in crystals of lithium niobate or gallium arsenide.

The Pockels effect, like the Kerr effect, is practically inertialess (speed is about 10 ^-10from). Due to this, it finds active use in the creation of optical modulators. The practical implementation of the effect is carried out by Pockels cells.



A quantum dot (QD) is a miniature piece of semiconductor material 15 nm in diameter and 5 nanometers (nm) thick, which, when a current is applied to it, can capture only one pair of electrons and holes.



There are two main methods for creating quantum dots:

1. epitaxy is a method of growing crystals on a substrate surface:
   
   
   
   
   • molecular beam and beam epitaxy;
   • gas phase epitaxy;
2. synthesis in colloid, in which substances are mixed in solution.

Colloidal synthesis can be used to obtain nanocrystals coated with a layer of adsorbed surface-active molecules. Thus, they are soluble in organic solvents, after modification - also in polar solvents.



Mainly compounds are grown from elements III (Ga, Al, In) and V (As, P, Sb) groups of the periodic table - the groups are designated AIII BV (or A ₃ , B ₅ ). Semiconductor lasers and microwave transistors have been created on the basis of such QDs.



Of particular interest are fluorescent quantum dots obtained by colloidal synthesis, for example, quantum dots based on cadmium chalcogenides, depending on their size, fluoresce in different colors. The phenomenon is familiar in practice even to children, as it is widely used in cell phones.



Physicochemical properties of quantum dots.



A wide absorption spectrum, which makes it possible to excite nanocrystals of different colors with one radiation source. A narrow and symmetrical fluorescence peak (without a “tail” in the red region, as in organic dyes, the half-width of the fluorescence peak is 25-40 nm), which provides a pure color: 2 nm points - blue, 3 nm - green, 6 nm - red.

High brightness of fluorescence (quantum yield> 50%). High photostability.



Functioning of a quantum communication channel (system). Individual photons of the light-emitting diode are focused by a lens and pass through the collimator, after which they enter the polarization device, where they are polarized to the required (one of 4 (|, -, \, /)) type using a cipher key. Photons move, maintaining polarization, along the channel of the communication system and on the receiving side again pass through the Pockels cell, after which they fall on a calcite prism (Wollaston), which divides a single photon flux into two, directing each to its own PMT. The latter, using the cipher key, read information, converting it into a message for the recipient.

Prerequisites for quantum computing

The idea of ​​quantum computing was expressed in 1980 by Yu. I. Manin [1] and in 1982 in an article by R. Feynman [2]. The emergence of quantum mechanics, within the framework of which results were obtained, inexplicable by classical mechanics, was the impetus for the development of not only physics, but also a number of other scientific areas, including quantum communication, computation, cryptology.

For the convenience of describing quantum concepts and phenomena in computing and manipulating variables by analogy with a digital binary bit (binary digits = bit), the concept of a quantum bit is introduced - a qubit.



Several physical models of quantum computing are also named: ion traps, photon qubits, topological qubits, etc.



Definition... A qubit is the smallest piece of information stored in a quantum computer. In accordance with the laws of quantum mechanics, a qubit can simultaneously be in two eigenstates, denoted | 0⟩ and | 1⟩.



A qubit can be any two-level quantum system, for example, a quantum particle with spin ± ½ in a constant magnetic field (electron, nucleus, photon). In this case, the state of the qubit can be specified by the superposition A | 0⟩ + B | 1⟩, where A and B are complex numbers satisfying the condition | A | ² + | B | ² = 1, i.e. the particle passes into one of the eigenstates with transition probabilities | A | ² in 0 and | B | ² in 1. The technique of computing with qubits is given in sufficient detail ( here )



The amplitudes of the probabilities are described by the formulas: A = cos (½θ); B = -e ^iφ sin⁡ (½θ).

Qubit construction. QC can be created using nanometer silicon planar integrated circuit technology. In this case, the requirements for isolating qubits from any degrees of freedom leading to decoherence must be met. If we consider qubits as spins on a donor in a semiconductor, then nuclear spins in the matrix represent a large reservoir with which donor spins can interact.



The spins in the matrix must be in the state I = 0. This important requirement excludes all semiconductors of the AIII BV types for matrix synthesis, since only silicon is stable isotope ²⁸Si with spin I = 0. Another requirement is deep cooling, the temperature must be so low that ionization of the donor is excluded. An important requirement in the case of considering two or more qubits is the requirement for the overlap of the regions of quantum Schrödinger wave functions.



The donor for Si (silicon) with spin I = ½ is a single ³¹ P (phosphorus) atom . For the ²⁸ Si: ³¹ P system at T = 1.5K and a low concentration of ³¹ P, the relaxation time of the electron spin is about 1000 seconds, and the relaxation time of the nuclear spin is ³¹P exceeds 10 hours. Quantum calculations are possible for nuclear spins when localized on a positively charged donor in a semiconductor matrix. Their temperature should be low enough (3-5 millikelvin), at which ionization of the donor is excluded.



The state of a photon cannot be read (measured) twice. An attempt to "intercept" the message will be noticed. When identifying (measuring) the current state of a qubit {| 0⟩ or | 1⟩}, the states should be physically distinguishable and estimated by probabilities. Such probabilities indirectly serve to estimate the initial (before measurement) state of the qubit. Qubits can be viewed as unit vectors in a two-dimensional complex vector space with an orthogonal fixed basis {| 0⟩} and {| 1⟩}. Quantum field theory considers particles as oscillations (quanta) of fields. Photon is a quantum of the electromagnetic field. Muon is muonic.



A superposition of states is something like a list of all possible states of a quantum object (let's say a photon). Before it was measured. It is not quite a wave and not quite a particle, but something else that has similar properties - “ripple, wavelet”.

When several qubits (register of qubits) are considered simultaneously, a change in the state of one of the qubits leads to a change in the states of others. They change in accordance with the first.



This connection is called entanglement of states, and the set of qubits is interpreted as a filled quantum register of a quantum computer. This register can be in various states and implement exchange and subtle physical dependencies between qubits.



Requirements for QC



The requirements and general conditions for creating a solid state QC are also formulated:

• «» ( );
• (100…1000Å) , , ;
• , (- );
• , () , ;
• , , ∆ = µgB, ∆N = =µNgNB, – , µ, µN – ; gN, g – g – ;
• () ;
• ( ), ;
• - - n- ;
• «» , , , , , CNOT π⁄8. .

Requirements for the processing of quantum information and its transmission (exchange):



a) The system must have the ability to reliably convert data stored in the form of stationary (computational) qubits into network (transmitted) qubits (for example, photons) and vice versa.



b) The system must be able to correctly transfer network qubits between endpoints.

Creation of QC and its elements

Quantum computers are developing at a rapid pace. QCs are created on several different principles: NMR - nuclear magnetic resonance, ESR - electron spin resonance, nuclear spin in silicon. A particle that generates a qubit can be an electron, a nucleus, a photon, capable of changing the spin state.



A quantum computer (QC) is a solid-state (semiconductor) device that uses quantum physical phenomena and the properties of electronic (nuclear) spins to perform computations in solving problems



There are many platforms on which to build a universal quantum computer. However, each approach has its drawbacks. For example, superconducting qubits have short coherence times compared to other realizations, and cold atoms are difficult to build a large quantum computer.

Quantum dots are a promising implementation of qubits, but they also have many problems. One of them is a qualitative measurement of qubits, which does not destroy the quantum state of the system. In this context, single electrons in quantum dots are considered as qubits, and states 0 and 1 are described by the electron spin.

A quantum computer on nuclear spins in silicon

The QC developers had something to build on in their activities. Nanoscale silicon planar integrated circuit technology works, functional requirements are listed, limitations and conditions are mostly defined. The Si: ³¹ P system was exhaustively studied about 60 years ago in experiments on electron-nuclear double resonance.





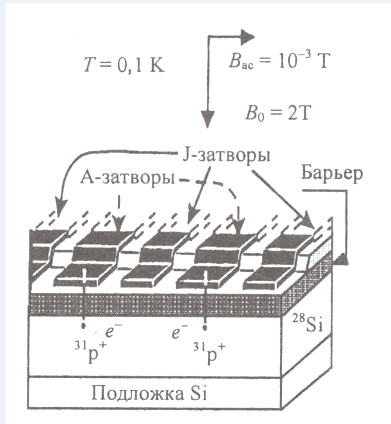
Figure A - Two qubits in a one-dimensional register (two ³¹ P donors with bound electrons embedded in ²⁸ Si)



At a low concentration of ³¹ P and at T = 1.5 K, the electron spin relaxation time is about 1000 s, and the nuclear spin relaxation time is ³¹ P exceeds 10 hours. When the temperature drops to 0.1 K, excluding ionization of the donor, the electron wave function is concentrated at the donor nucleus, which leads to a hyperfine interaction between the spins of the nucleus and the electron. The silicon plate is placed in a constant magnetic field Bo≥2T.



Two qubits in a one-dimensional register contain two ³¹ P donors with bound electrons embedded in ²⁸Si. They are separated from the control metal gates on the surface by a layer of SiO ₂ . A - electrodes control (set) the resonant frequency of the nuclear spin qubit; J - gates control the interaction of electrons of neighboring nuclear spins.

Electronic spin resonance quantum computer

When using ESD, the purity of the isotope of the silicon matrix is ​​not critical. For a number of indicators, ESR is preferable to nuclear spin, a magnetic field of 2 T (Tesla) provides an ESR frequency of 56 GHz, and due to the high Zeeman energy, electron spins allow operation up to frequencies in the gigahertz range. Nuclear spins are only up to 75 kHz. At T = 1 K, the spins of electrons (in contrast to nuclear ones) are completely polarized. Instead of silicon, Si / Ge heterostructures are used, which makes it possible to control the effective mass of the donor electron. J-gates of the cells are unnecessary. For measurements (reading the results), one can use not single-electron transistors, but ordinary field-effect transistors at low temperatures.





Figure B - Illustration of the method for detecting the spin state of an electron



A person cannot directly observe the states of qubits and quantum registers. When voltage is applied to both electrons and the gate antiparallel (singlet state) backs (left and right) are associated with one and the same donor (D ^- state) .They may execute transitions in a new state, which produces an electric current that measured with a capacitive device (single-electron transistor). This ensures the determination of the spin state of the electron and the donor nucleus ³¹ P. In this case, the Pauli principle is realized.





Figure C - Scheme of the exchange interaction between two qubits (two-qubit operation)



With an increase in the gate voltage, the binding energy decreases and the Bohr radius of hydrogen-like donors increases. In the xy-plane, electrons can be electrostatically attracted to one of the barriers formed by B-layers of the composition Si _0.23 Ge _0.77 . The Coulomb potential decreases V = -q / √ (r ² + d ² ), where r ² = x ² + y ² is the square of the horizontal distance from the donor, and d is the vertical distance from the barrier to the donor.

In this case, the energy of the Coulomb binding of electrons decreases and the overlap of their wave functions increases, allowing two-qubit operations to be carried out.



ESD design of a qubit

We will consider the structure of the KK register cell for two qubits. The ESD material cell is created by growing a Si / Ge solid solution on a silicon base (crystal), on top of which 5 more working layers are sequentially grown.





Figure E - The structure of the ESR cell for two qubits.



Left (a) - the energy profile of the Ge _{1 - x} Si _x heterostructure ; on the right (b) - cross section of a two-qubit cell. PT - field effect transistors; <111> - substrate orientation.



The main layers are T (tuning) "tuning" and D2-donor without breaks of conduction bands, where quantum calculations are performed (between 2000 Å atoms). The thickness and composition of the layers are determined by the energy diagram (left) and the requirements for the action of the control gates (above the layers). The T and D2 layers are enclosed between the barrier (their thickness is 200Å) layers, which prohibit electrons from moving vertically, differ in composition and have a different g-factor: g (T) = 1.563; g (D2) = 1.995 Electrons of the D2 layer play the role of qubits. The conduction band breaks equal to 20 meV implement the prohibition and conservation of qubit donor electrons, both carriers and quantum information.





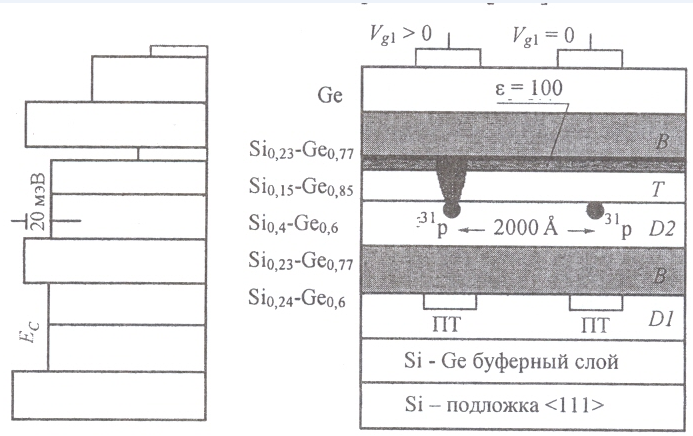
Figure E - ESD cell structure for two qubits. The designations of the previous figure are retained.



Consider the effect of the orientation of the crystalline silicon substrate. The orientation of the substrate, denoted by the symbol [001] (crystallographic theory), offers several advantages. the energy of the conduction band changes faster for this direction; solid compositions with lower voltages can be selected at a barrier height of about 50 meV, which is more than a 2-fold increase in comparison with the [111] orientation.



Accordingly, the barrier layers, while maintaining the same tunneling probability, can be thinner (miniaturization), and the allowable stresses are much higher. higher dielectric constant. With increasing distances, the exchange frequency between qubits decreases significantly.



For QCs based on NMR on phosphorus atoms in silicon, a solution was found to a rather complicated problem in the creation of qubits - the exact arrangement of donor atoms (up to 100 Å)





Figure F - Diagram of the process of constructing a register from NMR cells of qubits.



The diagram of the arrangement of individual phosphorus atoms in silicon has become realizable thanks to the advances in nanotechnology. The surface of the silicon wafer (Si [001] 2 × 1), cleaned under ultrahigh vacuum conditions, is passivated with a monolayer of hydrogen. Then, according to a special program, with the help of a scanning tunneling microscope probe, individual hydrogen atoms are desorbed in specified places. After that, phosphine vapor is introduced into the chamber at a pressure of 10 ^-8 mm Hg. Art. The adsorbed phosphine molecules then dissociate at a temperature of 500 ° C, leaving the phosphorus atoms bound to silicon at the sites of adsorption. After that, low-temperature silicon overgrowth of the resulting structure is performed.



It becomes possible to create a computer capable of parallel computing at the level of the entire computing device.



Let us list the factors and facts that increased the interest in QC, and the incentives for their practical development.



Algorithms have been created for quantum computers that solve difficult problems:

• search for items (brute force) in an unstructured database 1996 (LK Grover);
• modeling the evolution of quantum systems, for example, nuclear reactions;
• Large Number Factorization Problem (ZFBCH) 1994 (PW Shor);
• calculation of the discrete logarithm (DLOG) in a finite field, on an elliptic curve;
• and etc.

A procedure for controlling quantum states (correcting quantum errors) has been developed.



An experiment that implements quantum computations for the Grover algorithm and others on liquid nuclear magnetic resonance QC has been performed.



On the basis of solid-state elements, variants of CC structures were created:

• based on quantum dots (D. Loss, G. Burkard, L. Fedichkin, K. Valiev);
• based on superconducting Josephson junctions (DE Averin);
• on the nuclear spins of ³¹ P donor phosphorus atoms in isotopically pure ²⁸ Si (BEKane).
• on the electron spins of the same phosphorus atoms in epitaxial heterostructures
• Ge1-x Six (D. DiVincenzo).

Below are formulas for estimating the states of a qubit and their probabilities.

A quantum state is any possible state that a quantum system can be in. A pure quantum state can be described: 1) in wave mechanics - a wave function; 2) in matrix mechanics - by a vector.



Quantum computers promise to change a lot in our world. By their very nature, they are well suited to the computations required to invert one-way functions. For symmetric cryptography, this is not so bad. Grover's algorithm shows that a quantum computer accelerates attacks so much that the effective key length is halved. That is, a 256-bit key is as complex to a quantum computer as a 128-bit key is to a regular computer: both are secure for the foreseeable future.



For public key cryptography, the situation is more dire. Shor's algorithm easily breaks all popular public key algorithms based on both factorization and discrete logarithm. Doubling the key length increases the difficulty of cracking eight times. This is not enough for stable functioning (the error correction mechanism on a quantum computer can easily become an insurmountable problem for them).



Public key encryption (used primarily for key exchange)

The key word here is "key exchange" or, as they usually say, key agreement. And the encryption itself (AES, "Grasshopper", "Magma", etc.) is performed on symmetric keys (of course, with a periodic key change, all sorts of keymeching-b, maybe even generation for each packet). It is only about the encryption key.



In quantum physics (mechanics), there are a number of principles that are absent in traditional classical physics.



Heisenberg's uncertainty principle, it is impossible to simultaneously obtain the coordinates and momentum of a particle, it is impossible to measure one parameter of a photon without distorting another.

Pauli's exclusion principle states that two electrons (or any two other fermions) cannot have the same quantum mechanical state in one atom or one molecule.



In other words, no pair of electrons in an atom can have the same electron quantum numbers. The principle prohibits cloning (copying) of qubits.

Cloning is an operation on a pair or more of qubits, as a result of which a state is created that is a tensor product of identical states of subsystems.



The theorem on the prohibition of cloning (copying) is a statement of quantum theory that it is impossible to create an ideal copy of an arbitrary unknown quantum state of a particle. The theorem was formulated by Wutters, Zurek, and Dieck in 1982 and has been of immense importance in the fields of quantum computing, quantum information theory and related fields.



The state of one quantum system can be linked to the state of another system. For example, you can create an entangled state of two qubits using the one-qubit Hadamard transform and the hardware two-qubit quantum gate C-NOT. The result of such an operation will not be cloning, since the resulting state cannot be described in the language of subsystem states (the state is non-factorizable).





The difficult question is how to interpret the result obtained.



Advantages and disadvantages of quantum communication and QC over classical.



Positive aspects of using quantum systems.

• QC operates in calculations not with numbers, but with quantum states;
• in traditional (classical) physics, individual states of particles are combined using the usual scalar vector multiplication; in this case, the possible number of states of n particles forms a vector space of dimension 2 ⁿ ;
• () |0⟩ |1⟩ {|0⟩} {|1⟩}. . n ( n ) 2ⁿ. – {|0⟩ |1⟩} ; – {00, 01, 10, 11} . . ;
• m () 2^m . .
• .

The tensor product of states is the cause of EPR paradox and to some extent an explanation for it.

Tensor product

Consider the case of 2 qubits.





The case of 2 qubits. There are 4 options for their joint state.



These 4 vectors in the columns of the table are basic in the space of two qubits. Formally, it is described as follows. If there are spaces 1 and 2 with dimensions d1 and d2 and orthonormal bases {ei} and {fj}, then we can define a space with basis {$$$e_i⨂f_j$}, where i ranges from 1 to d1 and j ranges from 1 to d2.



If we introduce the scalar product on the new space according to the law

$$$⟨e_i⨂f_j│e_m⨂f_n ⟩=⟨e_i│e_m ⟩⋅⟨f_j│f_n ⟩⟨e_i⨂f_j│e_m⨂f_n ⟩=⟨e_i│e_m ⟩⋅⟨f_j│f_n ⟩$

and continue it to the other vectors, then the result is a Hilbert space, which is called the tensor product of H1 and H2 and is denoted $$$_1⨂ _2$... Obviously, its dimension is d1d2.



Tensor product of operators$$$_1 ϵ S(H_1 )$ and $$$_2 ϵ S(H_2 )$ Is the operator $$$_1⊗_2$ in space $$$_1⨂_2$acting under the law ($$$_1⊗ _2 )|e_1⨂e_2 ⟩=( _1│e_1 ⟩ )⨂( _2│e_2 ⟩$). The question arises as to whether any state in space$$$_1⨂_2$can be defined as the tensor product of states belonging to the partial spaces H1 and H2?



The answer to this question is negative, and a classical counterexample is the state in space of two qubits$$$_1^2 ⨂_2^2$, called EPR by the first letters of the surnames of the discoverers (Einstein, Podolsky, Rosen):



$$$|ψ_EPR ⟩= 1/√2 (|00⟩+|11⟩)$...



It is easy to see that this state cannot be represented as a tensor product of one-particle states:



$$$|ψ_EPR ⟩≠(a_1 |0⟩+b_1 |1⟩)⨂(a_2 |0⟩+b_2 |1⟩)$...

Quantum cryptology

Quantum cryptography (QCG) is a communication security method based on the principles of quantum physics. Unlike traditional cryptography, which uses mathematical methods to ensure the confidentiality of information, KKG focuses on physical phenomena, considering cases where information is carried using objects of quantum mechanics.



Quantum cryptanalysis (QCA). The widespread and development of quantum cryptography has caused the emergence of a counterweight - quantum cryptanalysis, which in some cases has, according to the theory, advantages over the usual. RSA and other number-theoretic ciphers and cryptographic methods based on the problems of factorizing large numbers, finding the discrete logarithm will lose their strength with the advent of quantum QCA.



According to the laws of physics, the state of a quantum of light (photon) cannot be read twice: after the first action on the photon, its state will change and a second attempt will give a different result. An attempt to "intercept" information will be noticed. Therefore, quantum cryptography is today considered the most promising direction of encryption.



To solve these problems, in particular, Shor's quantum algorithm (1994) was developed, which allows finding in a finite and acceptable time all prime factors of large numbers or solving the logarithm problem, and, as a result, breaking RSA and ECC ciphers. Therefore, building a large enough quantum cryptanalytic system is bad news for RSA and some other asymmetric systems. It is only necessary to create a quantum computer capable of executing the required algorithm.



As of 2012, the most advanced quantum computers were able to factorize the number 15 (in 150 thousand attempts, the correct answer was obtained in half the cases, in accordance with Shor's algorithm) and 21.



Protection of information (messages) from unauthorized access and from modification with The use of quantum objects was put forward back in 1970 by Steven Wiesner. Bennett S.N. and J. Brassard 10 years later proposed using these objects for transferring encryption keys in the form of quantum key distribution protocols - BB84 and later in 1991 and 1992 an improved protocol.



Quantum cryptography, along with the advantages and benefits, is characterized by certain limitations and negative aspects. As in any communication system in a communication system using quantum cryptography, there are nodes with user receiving and transmitting equipment, communication channels, energy sources, etc.



The negative aspects of quantum communication that are noted are usually the following.



Complex equipment must be installed on both sides (transmitting and receiving) of a channel of a quantum communication system:

• imperfection of sources of single photons (low generation rate);
• the photon polarization control system is poorly protected from interference;
• imperfection of receivers of single photons, sensitive detectors work in addition to photons and on other particles;
• , ; ;
• 100 ( 100 ) , ( , , );
• ;
• ( $81000).

To measure the polarization angle of photons, you need to know exactly how the equipment is oriented at both ends of the channel. These conditions limit the spread of quantum cryptography to mobile devices.



Over time, an acceptable option was found. Complex equipment can be installed by only one user, at one end of the channel. Another user accepts a signal and only modifies the state of the photons, adding his information to the changed states. The changed photons are sent back. Such equipment is already able to fit in a pocket device.



As for establishing the orientation of the equipment, it is proposed to carry out measurements in random directions, and their list should be published openly. For legitimate work and decryption, use only directions that match subscribers. The method is called “quantum key distribution independent of the reference frame”.

Quantum key distribution

Quantum Key Distribution (QKD) is a key transfer method that uses quantum phenomena to ensure secure communications. This method allows two parties, connected through an open communication channel of fiber optic or free networks to transmit a stream of photons, to create a common random key, which only they know, and use it to encrypt and decrypt messages.



The main goal of the known quantum key distribution (QKD) protocols is to match random transmitted sequences of particles (photons).

In 1935, Einstein and a group of like-minded people, trying to challenge the Copenhagen interpretation of quantum mechanics, formulated a paradox, later called the Einstein-Podolsky-Rosen paradox (EPR paradox tensor methods do not describe all states of qubits).



Among the possible QKDs, the early BB84, B92 (Bennett), B91 (Eckert, another name for EPR), later CW (continuous variables), the Swiss protocol COW (Coherent One Way-coherent one-way encryption), Lo05 (created by Lo H.-K. Ma K. and Chen K. 2005), SARG, Decoy State, DPS (differential Phase Shift), with reference state, phase-time.

Charles H. Bennett's Algorithm. Some of the listed protocols are discussed in detail below.

Quantum protocol BB84

Example 1 . Implementation of quantum cipher key distribution (BB84 protocol), which uses orthogonal states of quantum objects. The recipient of the message acts on objects (photons), randomly choosing the type of measurement: it changes either the linear polarization of the photon (|, -), or the diagonal (\, /)



IMPLEMENTATION OF THE QUANTUM PROTOCOL BB84





Lo05 and E91 protocols . This protocol was developed by Arthur Eckert in 1991. It also has the name EPR (Einstein-Podolsky-Rosen) as it is based on the Einstein-Podolsky-Rosen paradox. Lo05 is a quantum cryptographic key distribution protocol created by the scientists of Luo H.-K. Ma K. and Chen K. Quantum Key Distribution (QKD) allows two users, a sender and a receiver, to communicate in absolute safety in the presence of an intruder.



In 1991, Bennett suggested using the following algorithm to record changes in data transmitted using quantum transformations:

1. The sender and receiver agree on arbitrary permutation of bits in the strings to make the error positions random.
2. k (k , ).
3. . .
4. , , .
5. , , k.

In order to determine whether or not undetected errors remain, the receiver and the sender repeat pseudo-random checks, namely: the receiver and the sender openly announce the random mixing of the positions of half of the bits in their strings; the receiver and the sender openly compare parities (if the strings differ, the parities must not match with probability 1/2); if there is a difference, the receiver and the sender, uses binary search and invalid bit removal.



If there are no differences, after m iterations the receiver and the sender receive identical strings with an error probability of 2 ^{- m} .



Quantum Protocol B92Is one of the first protocols for quantum key distribution, which was proposed in 1992. C. Bennett. Hence the name B92, by which this protocol is known today. The B92 protocol is based on the principle of uncertainty, unlike protocols such as E91. Information carriers are 2-level systems called qubits. An important feature of the protocol is the use of two non-orthogonal quantum states.





Example 2 . Implementation of the quantum distribution of the cipher key (B92 protocol), which uses orthogonal and non-orthogonal quantum states (photon polarizations).





1. In the case of an EPR implementation, the sender randomly chooses a basis for measuring the state of one photon from an EPR-correlated pair, either linear or circular.



2. In the second step, the sender's actions depend on the protocol version.



a) for EPR implementation, selects a random sequence of bases for measuring the polarization of photons;



b) The sender selects a random sequence of polarized photons and sends them to the receiver.



3. The receiver measures the polarizations of the arriving photons using a sequence of random bases.



4. The results of measurements of the recipient (not ideal source, communication channel and detector lead to the loss of photons).



5. The receiver informs the sender of the basis for measuring the polarization of each received photon.



6. The sender informs the recipient which bases the recipient has chosen correctly.



7. The sender and receiver store the photon data measured in the correct polarizations and discard all others.



8. The rest of the data is interpreted in accordance with the code table:



9. The sender and the receiver check their keys against the parity of the selected subset of bits. If even one bit is different, then such a check shows the existence of an intruder listening on the channel.



10. Sides discard one of the bits of the selected subset.

As a result of communication under the B92 protocol, the sender and the receiver receive a shared secret key 0101101 and reveal the absence of an intruder with a probability of 1/2.

Quantum COW protocol

Example 3 . Implementation of quantum cipher key distribution (COW protocol), which uses coherent one-way encryption.



The sender sends "0" with probability (1 - f) / 2, "1" with probability (1 - f) / 2 and control states (decoy) with probability f.



The receiver announces which bits of the sequence it has measured in the timeline and when the DM2 detector lights up, it returns the sequence to the sender.



The sender performs (Key sifting) - tells the receiver which bits he needs to exclude from his raw key, since they are due to the detection of control states.



Sender. Analyzing triggers in DM2, it evaluates coherence violations through the visibility V1−0 and Vd and calculates the intruder's information.



Error correction in progress. Strengthening the secrecy of the sifted key An



interesting fact of "canceling the collapse" of the wave function is given by Korotkov and Jordan.



They drew attention to him and conducted an experiment that tests and allegedly confirms the theory. But apparently, one confirmation is not enough, and no one has published any ideas or applications about the use of the fact. I simply could not fail to mention this.

Cancellation of collapse by the experience (2008) of the Nadav Katz group, which confirms the correctness of the Korotkov-Jordan theory (2006) escape from the collapse by multiple returns of the qubit state.

In general, any quantum system is in a superposition of all its possible states until a measurement occurs and it assumes one of the possible states. After measurement, the system will assume a specific state (collapse).



And so, in 2006, Korotkov and Jordan publish an article titled "Uncollapsing the wave function by undoing quantum measurements", which in Russian can be roughly translated as "Canceling the collapse of the wave function by canceling the quantum measurement." or arXiv: 0708.0365v1 [Quant-Ph:

Cryptoanalytic vulnerabilities, attacks, their classification

Experts believe that quantum key distribution is not invulnerable to hacking, but quite accessible to an intruder. Another thing is that the actions of the intruder can be detected, and the key is not required and replaced with another. Specific implementations of such systems allow a successful attack and steal the generated key.



A fairly extensive list of attacks is possible.



Attacks on equipment of a quantum system:

• use of a beam splitter;
• using a powerful pulse (blinding avalanche photodetectors);
• use of the spectrum of photon sources, if they differ;
• the violator's use of a PRNG similar to that of the sender.

Attacks on the state of quanta (photons):

• using coherence;
• coherent attacks consider relay tactics;
• incoherent attacks: relay interceptor; using photon cloning;
• - combined attacks:
  
  
  
  - interaction with individual qubits;
  
  - measurements of their arrays.

Three examples of implemented attacks (from publications on the network)

Beam splitter attack on COW

It is assumed that the intruder's resources are unlimited. Attacks on key distribution protocols: a general scheme for preparing and measuring quantum states, a procedure for obtaining results of measurements of quantum states of a key on the sender and receiver sides. Attacks on the technical implementation of quantum cryptographic systems (quantum hacking).

• Attenuation ⇒ µB = 10 − δl / 10µ;
• Beam splitter + ideal communication channel;
• µ max E = µ - µB = (1 - 10 − δl / 10) µ.

In the February issue of the journal "Quantum Electronics" (among the founders - the leading physics institutes of the Russian Academy of Sciences), a method is described - how to read a message transmitted over a quantum communication network, implemented using Swiss technology, and remain unnoticed. As it is written in the article, “the main idea of ​​the attack is to individually measure a part of the intercepted states and send the rest of them unchanged. The authors have calculated the optimal values ​​of the attack parameters for an arbitrary length of the communication channel. "



The Russian development has a greater protective potential for creating multi-user networks due to a special way of transmitting several channels over one line. This allows you to significantly increase the speed or bandwidth of the quantum channel, the developer believes.



Another example is the PNS-attack (Photon number splitting attack) [1], carried out by physicists from Australia and Japan, who for the first time carried out a quantum non-destructive measurement of a qubit, which consisted of one electron in a quantum dot. Scientists have shown that the reliability of such a measurement is over 99.6 percent. The article was published in Nature Communications.



Scientists from Australia and Japan, led by Professor Seigo Tarucha of the RIKEN Science Center, proposed measuring a qubit in a quantum dot using another electron entangled with a qubit. This implementation allows the state of the working qubit to be preserved for a long time, which is necessary, for example, for the implementation of error correction codes.



To test the non-destructive readout, physicists placed two electrons in Si / SiGe quantum dots - one of the electrons used as a working qubit and the other as an ancilla for the measurement. The scientists controlled the connection of the qubits with a magnetic field created by a micromagnet on a chip.







A diagram of the physical implementation of two qubits, representing two electrons that scientists have placed in quantum dots. J. Yoneda, et al. - Nature Communications 11, 1144 (2020)



Literature:



D.A. Kronberg, Yu.I. Ozhigov, A.Yu. Chernyavsky. Quantum cryptography. - 5th ed. - MAKS Press, 2011 .-- S. 94-100. - 111 p. Archived November 30, 2016

Bennett CH, Brassard G. Quantum Cryptography: Public Key Distribution and Coin Tossing // Proceedings of International Conference on Computers, Systems & Signal Processing, Dec. 9-12, 1984, Bangalore, India. - IEEE, 1984. - P. 175

Bennett, CH and Brassard, G., Conf. on Computers, Systems and Signal Processing, Bangalore, India, 175-179 (1984).

Bennett CH Quantum Cryptography using any Two Nonortogonal States // Phys. Rev. Lett. 1992. Vol. 68, 3121.

Ekert AK, Hutter B., Palma GM, Peres A. Eavesdropping on quantum-cryptographical systems // Physical Review A. - 1994. - Vol. 2, No. 50. - P. 1047-1056

Einstein A., Podolsky B., Rosen N. Can quantummechanical description of physical reality be considered complete? // Phys. Rev. A - 1935. - Vol. 47, 777.

Shor PW Scheme for reducing decoherence in quantum computer memory // Phys. Rev. A 1995. Vol. 52, 2493.

Shor PW Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer // SIAM J. Sci. Statist. Comput. 1997. Vol. 26, 1484.

Shor PW, Preskill J. Simple proof of security of the BB84 quantum key distribution protocol // Phys. Rev. Lett. 2000. Vol. 85, 44